基于sinh-sigmoidal组合式变换的薄型结构边界元分析方法*

张亚萍

(泰州职业技术学院 智能制造学院,江苏 泰州 225300)

0 引 言

作为一种可拆卸的静密封连接结构,垫片-法兰-螺栓连接是石油管道及化工设备中必不可少的重要部件,目前已被广泛应用于机床装备、航天航空等众多工业领域[1-4]。

结构的密封性能直接影响工业生产安全和企业生产利益。垫片作为连接结构中的重要密封元件,其弹性力学性能也受到了普遍关注。

常见的密封方式是通过对上法兰中的螺栓垫片施加预紧力。随着所受预紧力的逐渐增大,垫片在受压后,会表现出高度的非线性与复杂的时滞性。因此,准确评估初始预紧力及最大位移载荷下的压缩回弹性能是保证其密封性能的重要前提[5]。

研究者们一直致力于厘清影响垫片-法兰-螺栓连接结构密封性能及连接可靠性的影响因素,并不断优化静密封连接结构设计的计算方法和相应的试验标准,以期建立起严谨有效的连接设计体系。欧美和日本等国家和地区已经建立了基于泄漏率的垫片参数以及垫片压缩回弹性能试验方法,并形成了相应的体系标准[6-8]。这套体系标准在测试垫片参数时,均假设施加在垫片上的应力是均匀分布的。

然而,在实际的生产工作中,种种因素的影响会导致法兰发生偏转,通过螺栓施加在垫片表面上沿径向分布的接触应力是不均匀的。针对这一现象,现有文献中普遍采用有限元法(FEM)对垫片的接触应力进行数值分析。

王璐等人[9]运用ABAQUS分析了当各螺栓施加的预紧力产生差异时,垫片接触应力的分布情况。卢志珍、朱乐等人[10-11]运用ANSYS自带的衬垫单元模型Gasket,向垫片施加位移载荷,且步长为2 s,从而得出垫片的压缩回弹性曲线,借此分析其密封性能。喻健良等人[12]运用ABAQUS,分析了不同加载方式和垫片型式对螺栓交互作用的影响。OMIYA Y等人[13-14]运用ABAQUS,分析了在各螺栓预紧力相同的情况下,垫片的接触应力分布情况,并通过实验对此进行了验证。

有限元法是目前一种主流的数值分析方法,并已经得到了广泛的应用。但在计算薄壁结构、应力集中、无限域等问题时,其计算精度及计算效率较低。为弥补有限元法的不足,近年来诸如无网格法[15]、边界元法[16-19]等数值分析方法取得了长足进步,各个瓶颈问题也相继得到了解决。

边界元法(BEM)是在边界积分方程理论基础上建立起来的一种纯边界离散型数值分析方法。相较于其他数值分析方法,其具有离散单元数量较少、数据准备简单、计算量小的优势。但利用BEM分析垫片等薄型结构的弹性力学问题时,求解的大量近奇异积分会出现近奇异性,且被积函数会随距离的减小而急剧变化,需要大量高斯积分点才能获得较好的计算精度。这一情况严重影响了该方法的计算效率。

针对薄型结构分析中的积分近奇异性消除问题,SLADEK V等人[20]于1993年提出了正则化法。2014年,ZHANG Xi-yu等人[21]也提出了一种基于薄型结构混合边界节点法的理论分析方法,数值算例表明了该方法具有一定的适用性。2019年,张见明等人[22]提出了一种新的单元细分法(基于体二叉树),大幅提高了奇异和近奇异积分的计算稳定性及精度。

在不同的方法中,非线性变换法能更好地利用计算机软件,对其进行模块化编程,并且可以不依赖积分核函数;但其计算精度和稳定性受到积分域内部投影点位置的影响。

笔者将针对弱化投影点影响力的新型非线性变换法进行研究,提出一种非线性组合式sinh-Sigmoidal变换方法,并将其集成到边界元程序,以消除积分在径向和角度方向的近奇异性;然后,分别在理想工况和实际工况下,采用BEM和FEM程序分析薄型垫片的弹性静力学特性,以验证该方法的有效性。

1 边界元法

笔者以弹性力学问题为例进行说明,将边界元法应用于实际力学问题的求解。

经典弹性力学问题的平衡方程和边界条件描述如下[23]:

(1)

其中:对于三维问题,均采用指标形式记法,下标i,j=1,2,3表示对其所代表的变量求偏导数,即σij,j=∂σij/∂xj。

同一变量中,若下标重复出现即表示求和,其几何方程和物理方程如下:

(2)

式中:δij为Kronecker符号,当下标i=j时通常取值为1,否则为零;λ,μ均为Lame弹性常数。

λ,μ与弹性模量E、泊松比ν以及剪切模量G之间的关系如下:

(3)

经典弹性力学问题相应的边界积分方程常表示如下:

(4)

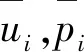
对于三维各向同性体,其基本解为开尔文(Kelvin)解。位移和面力的基本解表示如下[24]:

(5)

(6)

式中:r(x,y)为源点y与场点x间的欧几里得距离。

其中:位移的基本解满足爱因斯坦求和约定,当l=i时,δli=1,其余情况取值均为零。

假设源点y位于光滑的积分边界上,则取系数clj(y)=1/2。在不考虑体力影响的情况下,可得只包含边界积分项的积分方程,通过单元插值法将所求解的具体问题的边界进行离散化处理。

对位移和面力进行等参差值计算如下:

(7)

(8)

式中:m为边界离散的单元总数量;Nk(ξ,η)则为离散单元内部第k个插值点所对应的形函数。

笔者通过广义达菲变换,将坐标转换至(ξ,η)空间,得到了正则化的参数坐标。在给定的相应边界条件下,将场点x取遍积分单元内所有插值点的位置,可得3N×3N规模的线性方程组(其中,N为总的插值点数量)。

通过计算机编程求解,笔者可得边界上任意未知的位移或面力值。而弹性体内任意一点的位移、应力、应变的值则可以根据式(4)计算得出。

2 sinh-sigmoidal组合式变换法

笔者利用BEM分析薄型结构的弹性力学问题,求解大量的近奇异积分,公式如下:

(9)

式中:f为不存在近奇异性的光滑函数;x为域内被积点;y为域外源点;r为两点间的距离。

当分母rl趋近于零时,积分在径向和角度方向均会出现近奇异性,被积函数随距离的减小而急剧变化,需要大量高斯积分点才能获得较好的计算精度,但其严重影响了计算效率。

因此,精确高效地求解近奇异积分是利用BEM分析薄型结构问题的关键。基于自适应分块技术和不同坐标变换,笔者提出一种非线性sinh-sigmoidal组合变换法,将其与原始极坐标变换下(ρ,θ)坐标空间中的近奇异积分相结合,可以在提高积分计算精度的同时大幅降低计算量,弥补传统变换法的不足。

2.1 原始极坐标变换

局部坐标系中的距离函数如图1所示。

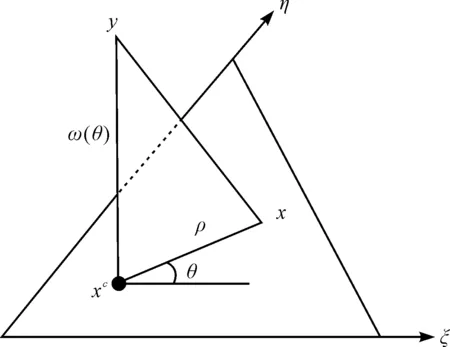
图1 局部坐标系中的距离函数

在三角形单元中,距离源点y最近的点为投影点xc,两者的连线垂直于积分单元中xc处的切线。

根据源点y的位置,即可确定投影点xc的位置。在投影点附近使用泰勒公式展开如下[25-26]:

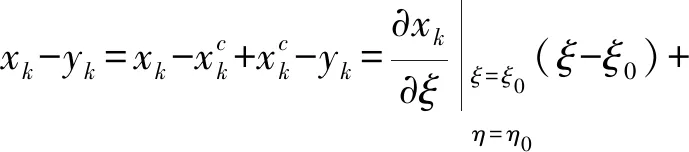
(10)

式中:(ξ0,η0)为投影点在局部空间坐标系(ξ,η)内的参数坐标。

以(ξ0,η0)为极坐标原点变换所得,则ξ、η的表达式如下:

(11)

将式(11)代入式(10)可得:

(12)

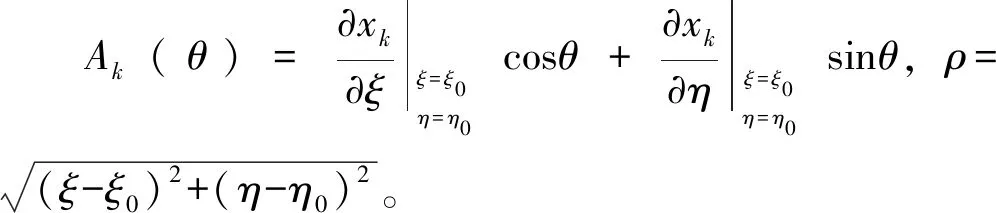
从源点y到场点x的实际距离r又可以表达如下:

(13)

其中:ω(θ)=r0/A(θ),A(θ)=|Ak(θ)|。

在局部坐标空间系(ξ,η)中,笔者对近奇异积分的一般形式即式(9)进行原始极坐标变换,其表达式如下:

(14)

由式(14)可得,原始极坐标变换将积分空间从(ξ,η)转换至(ρ,θ),且径向和角度方向上均出现了积分近奇异性。

2.2 径向变换

为保证投影点位于积分形状良好的子三角形单元内部,降低积分形状对计算精度的影响。笔者对每个积分单元运用自适应分块技术,将sinh变换重新定义如下:

r(s)=ω(θ)sinh(μ1s-η1)

(15)

将积分区间[0,ρ(θ)]和[θm,θm+1]分别转换至区间[-1,1],可得:

(16)

因为投影点位于积分单元边界的高阶近奇异积分精度不够,所以迭代sinh变换是必要的。其公式如下:

s(u)=a+bsinh(μ2u-η2)

(17)

其中:a=-1,b=π/2μ1。将引入的新变量的积分区间转换至具体区间[-1,1],简化编程过程,可得下式:

(18)

将式(15)和式(17)代入式(14),可得:

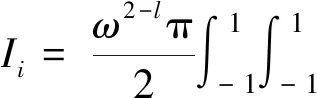
(19)

笔者将上述积分区间从未知量转换成已知量,可消除积分核函数在径向上的积分近奇异性;但角度方向的积分近奇异性依然存在。

2.3 角度方向近奇异性

在典型的sigmoidal变换中,其核函数能有效地向积分区间两端大量聚集高斯积分点。利用这个特点,可将其应用于消除角度方向积分近奇异性。常用变换式如下:

(20)

式中:w为变换变量的幂指数,且w≥1。

由此又可得到:

(21)

为了消除积分的双向近奇异性,并提升计算的精度,将式(21)代入式(19),可得:

(22)

在上述转换过程中,通常取w=2,以获得满意的精度。

3 薄型垫片弹性静力学特性分析

3.1 理想工况边界元分析

根据上下表面及内外环设定的边界条件,以及无体力项的弹性力学边界积分方程,笔者对垫片所有边界节点处面力的变化情况进行多方向分析,并通过不断加大网格划分密度和增加计算节点数量,以此来验证边界元法的收敛性。

笔者对该薄型垫片的各个面施加x、y、z方向的位移边界约束条件,如下:

(23)

为了验证边界元法计算所得结果的收敛性,笔者取4种不同的网格尺寸以及单元、节点数量,对薄型垫片所有边界计算节点进行x、y、z方向上面力变化情况的误差分析。

边界节点各方向面力的平均误差计算结果如表1所示。

表1 边界节点各方向面力的平均误差计算

边界节点各方向面力的平均误差值分析结果如图2所示。

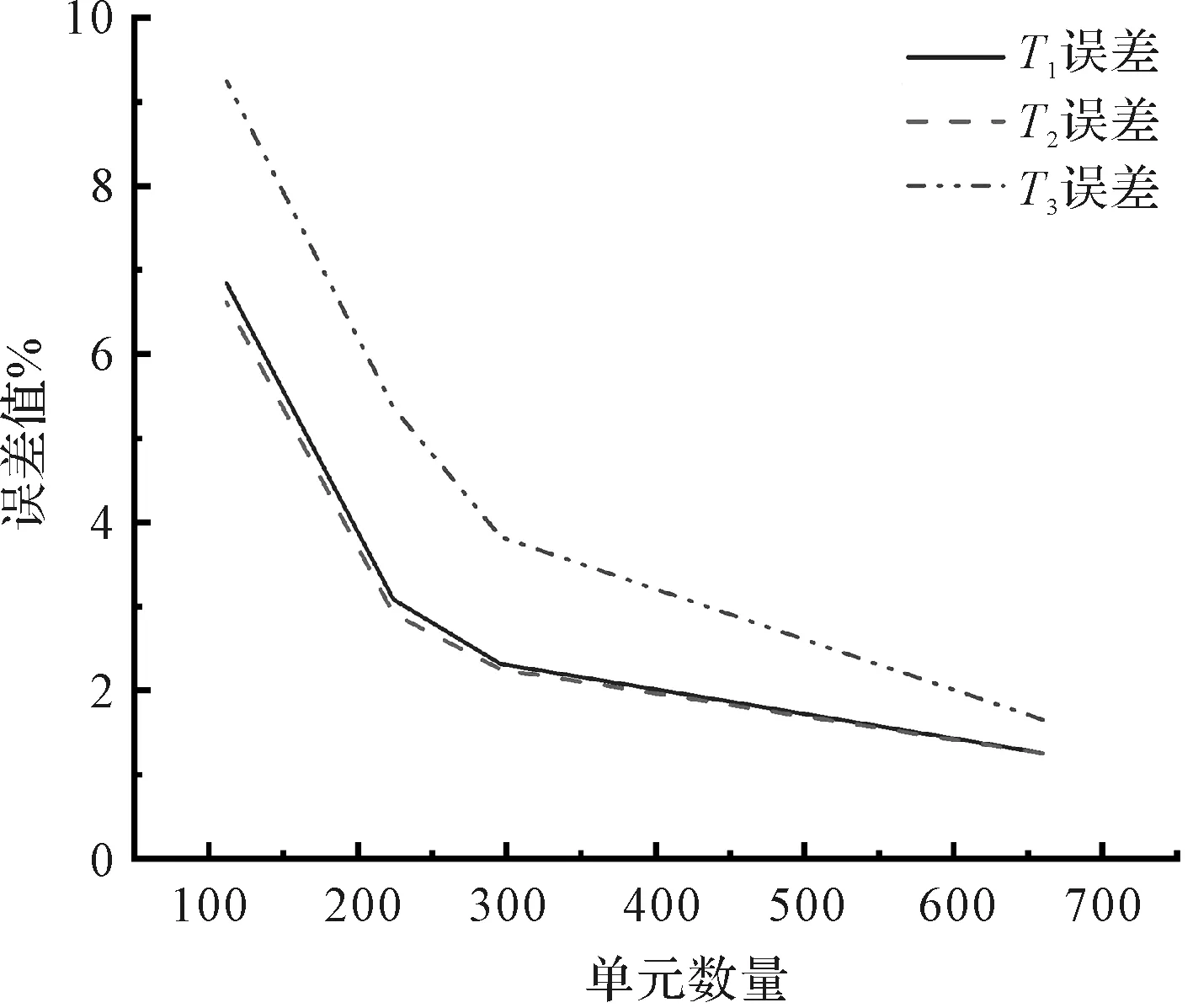
图2 边界节点各方向面力的平均误差值分析

图2中结果显示:随着网格尺寸的不断细分,单元和节点数量的不断增加,计算节点处的误差值不断减小。

运用BEM程序计算可得,x、y、z方向上节点位移的数值结果能有效地收敛到精确解,说明该方法在分析薄壁结构弹性力学问题时是精确可行的。

3.2 实际工况垫片受力变形分析

上述结果已经验证了边界元法在理想工况下(在各方向边界条件均可以用公式描述),分析薄型垫片所得结果的有效性与正确性。

为进一步验证该方法在实际工况下同样具有可行性与一定的精度,笔者分别采用两种方法(BEM、FEM)分析计算垫片受外力影响下的变形情况。

薄型垫片的约束条件及载荷施加如图3所示。

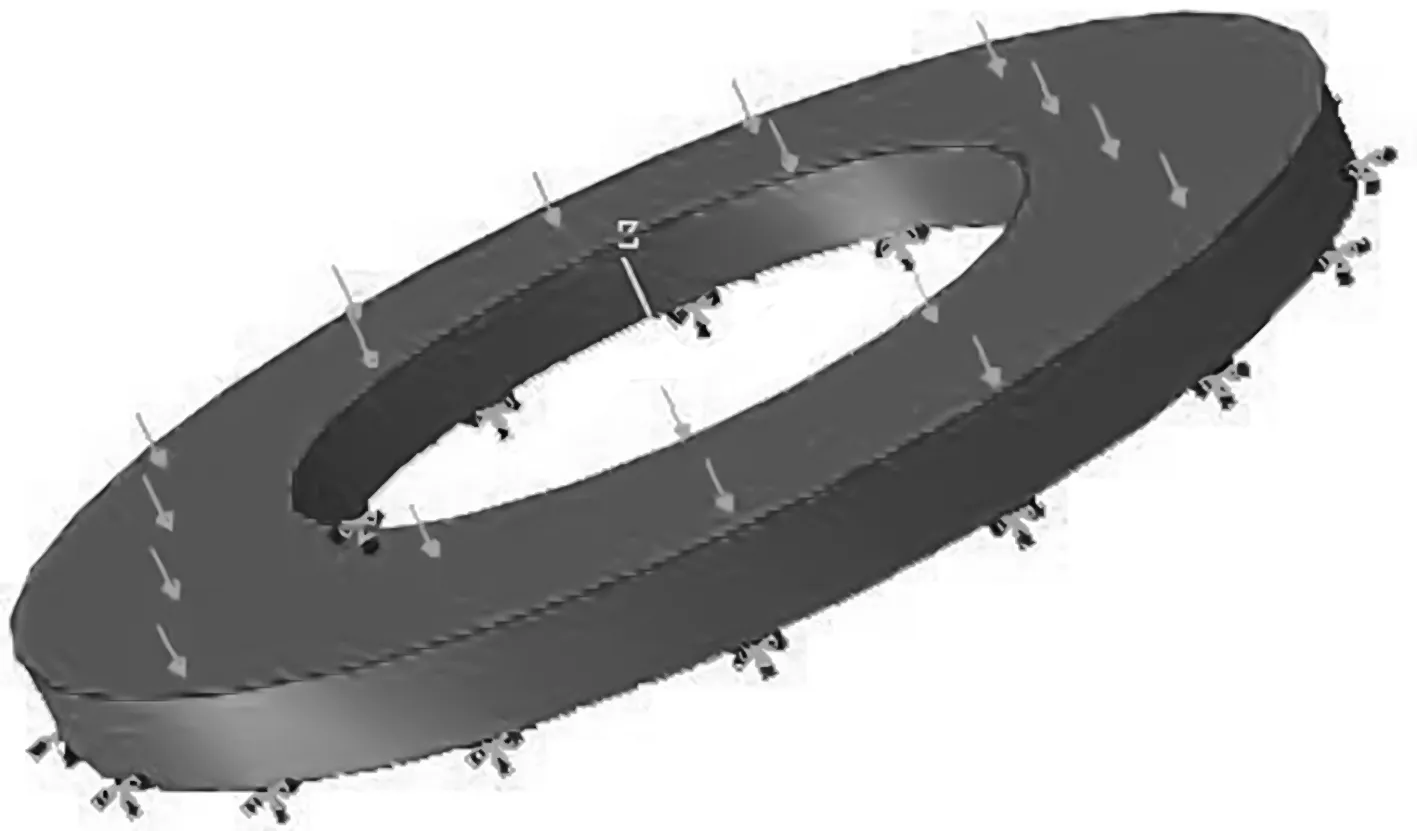
图3 垫片模型受力情况

因薄型垫片的结构轻量化,此处不考虑自重产生的变形。笔者将其一端面固定,另一端面施加压力。

边界元法程序网格划分如图4所示。

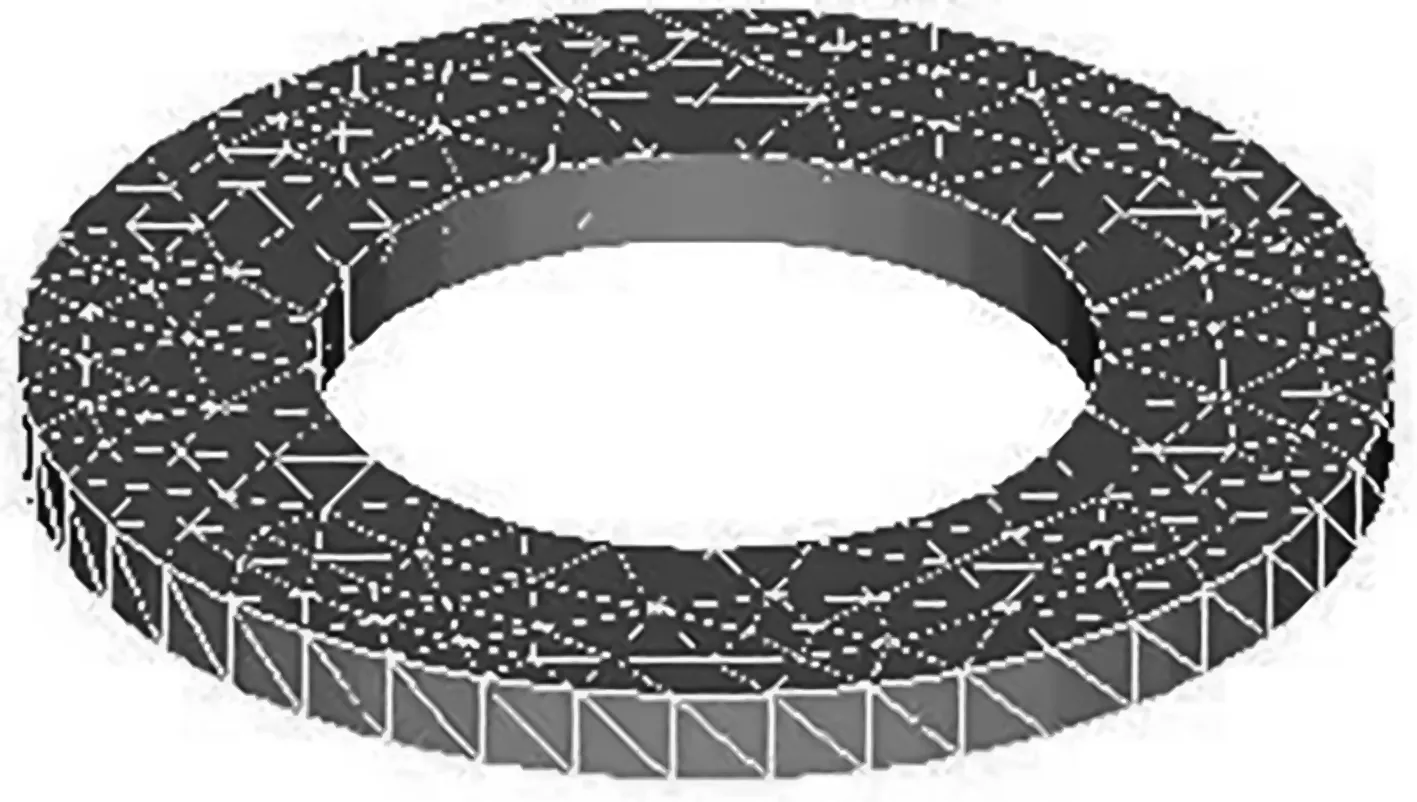
图4 边界元法网格划分

为了获得更为精确的变形结果,笔者在边界元法分析中使用了1 296个三角形单元,域内及表面共计使用2 113个节点。

笔者采用ABAQUS有限元软件对垫片模型进行网格划分,其结果如图5所示。

图5 有限元法网格划分

在有限元法分析中,笔者共计使用了126 350个线性六面体单元(C3D8R)以及142 791个节点。

采用ABAQUS有限元软件对模型进行分析,可以得到z方向的位移变形云图,如图6所示。

图6 基于有限元法的z方向位移云图

垫片在z方向位移变形范围区间为[-2.069,0]。

为进一步验证边界元法分析的精确性和高效性,笔者在其厚度方向均匀选取10个取样点,并进行对比分析。

样点坐标及计算结果对比数据如表2所示。

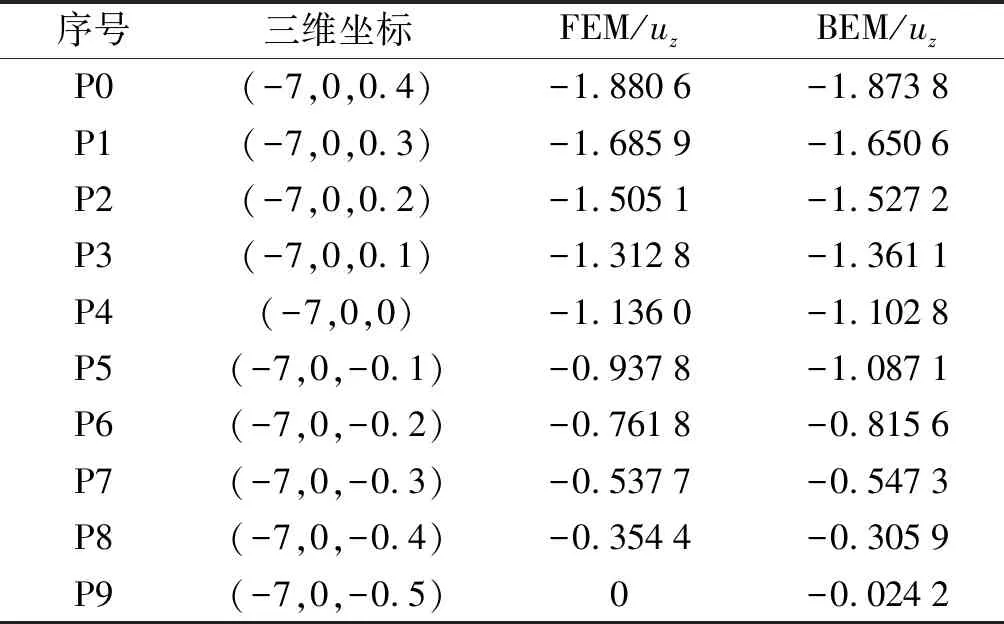
表2 样点坐标及2种方法计算结果对比

由表2数据可知:采用边界元法,以极少的单元和节点数量计算所得z方向位移的变形结果,与采用有限元法分析所得到的结果相近。

厚度方向FEM与BEM的位移计算结果对比如图7所示。

图7 厚度方向FEM与BEM的位移计算结果对比

由图7可知:运用BEM程序计算得到的样点处z方向位移线性图,与ABAQUS软件计算所得图形趋势基本吻合,并且从10个取样点的具体数据值而言,上述2种方法间的计算误差均小于1%。

由此可见,该算例也充分验证了边界元法在实际工况下分析薄型垫片弹性力学问题的高效性以及精确性。

4 结束语

针对薄型结构边界元数值分析过程中的近奇异积分计算困难问题,笔者提出了一种基于sinh-Sigmoidal组合变换的解决方案,消除了积分在径向和角度方向的近奇异性,并提高了边界元法的计算效率和计算精度。

通过将其与有限元分析方法(FEM)进行比较,结果验证了该方法的有效性,其是一种适用于薄型垫片弹性静力学问题的有效数值分析方法。

研究结论如下:

1)采用迭代sinh变换可消除积分的径向奇异性,采用Sigmoidal变换可消除角度方向奇异性;

2)通过理想工况下的薄型垫片算例分析,验证了BEM在计算垫片结构面力时的收敛性和正确性;

3)通过实际工况下的薄型算例分析,对比了10个取样点处BEM和FEM的位移计算结果,计算误差均小于1%;但BEM方法的计算效率优势明显,验证了BEM计算的高效性以及精确性;

4)在薄型垫片的设计中,可利用BEM对垫片进行弹性力学分析,得到在表面预紧力作用下的变形曲线,再进行相应的补偿设计,以保证薄型垫片的连接可靠性,提高其密封性能。

当前的研究主要考虑的是投影点位于积分单元内部的情况。对投影点位于外部的情况,有待笔者进一步深入研究。同时,由于在当前研究中,所分析对象为结构简单的圆形薄垫片,要使BEM方法能得到广泛的应用,未来还需针对更复杂的结构开展研究。