可控型静压气体密封结构参数对密封性能的影响实验研究*

闫欣欣,郑 娆,李双喜*,贾宇宁,陈 杨,李梦竹,张敬博

(1.北京化工大学 机电工程学院,北京 100029;2.上海天马微电子有限公司,上海 201201;3.中国船舶集团有限公司 系统工程研究院,北京 100094;4.北京北方华创微电子装备有限公司,北京 100176)

0 引 言

可控型静压密封是借鉴静压轴承相关理论发展而来的一种非接触型密封形式[1]。在密封状态下,其闭合力与开启力由同一组密封气调节,达到了对端面气膜[2]的控制效果,使密封气体得到了最大程度的利用,符合当今社会倡导的工业节能与绿色发展的理念[3]。

可控型静压密封具有泄漏量低、开启力高和气膜刚度大的特点[4]。但由于运行时的工况条件不断发生变化,可控型静压密封经常会存在泄漏失效问题[5]。如何在确保密封性能可靠性的同时,降低其加工技术难度,提高低转速设备的密封稳定性[6-7],同时又能保证设备的安全运行,已成为静压密封研究的重要方向[8]。

李双喜等人[9]提出了一种新型混合式密封方法,通过分析得到了其气膜压力分布状态和运行工况下的密封性能参数;但是该方法仅探究了动压密封的螺旋槽结构,没有对静压密封相关槽型结构的混合密封性能进行研究。张树强等人[10]通过将摄动法移植到混合式密封追随性的过程,分析了静环的轴向自振稳定性,提出了临界失稳判据;但该研究仅验证了一种典型结构,未对其他结构参数在混合式密封性能上的影响做出说明和解释。

郝战焱等人[11]基于气体润滑理论,采用平衡膜厚度作为调控指标的方法,研究了实际工况下调控比对密封性能参数的影响规律,推导出了正交坐标系下的密封调控方程;但是该研究中的节流孔数一定,难以说明不同节流孔数量下调控指标的适用性。车健等人[12]基于大涡湍流模型,研究了节流孔的出气模式对静压干气密封的影响,以及节流孔位置和气膜厚度对单列孔节流静压干气密封稳态性能的影响;但该研究中并没有分析节流孔数量对气膜厚度和密封稳态性能的影响。

STOLARSKI T A等人[13]提出了均压槽概念,发现了均压槽可以提高密封端面的气膜刚度,并且获得了更大的开启力;但该研究仅分析了均压槽位置和均压槽高度对密封性能的影响,忽略了均压槽宽度对密封性能的影响,因此,该研究的结论缺乏全面性。XU H J等人[14]采用实验的方法,研究了均压槽的径向槽宽比对干气密封性能的影响规律;但其没有分析均压槽几何尺寸对气膜膜厚和开启力的影响。王婷等人[15]基于微型机床的气浮导轨模型,研究了不同结构的均压槽对轴承承载能力的影响,发现了直线型均压槽的气膜压力分布更加均匀,压力下降速度更加缓慢;但该研究中的均压槽位置固定,不足以说明当均压槽位置发生改变时,气膜压力的分布效果与当前研究结果具有一致性。

总体而言,前人对静压密封性能的研究主要集中于单一的结构参数,没有对多结构参数下的密封性能展开研究,导致其研究结果缺乏普适性,难以获得最佳的静压密封结构。

因此,笔者采用有限元数值分析软件,建立可控型静压密封气膜流场模型,针对不同结构参数下的可控型静压密封性能进行研究,分析密封端面结构参数对可控型静压密封性能的影响程度,揭示结构参数对可控型静压密封的影响机理,以获得最佳的参数区间;最后,采用试验的方法对数值模拟结果的准确性进行验证。

1 密封原理与密封性能参数

1.1 密封原理

可控型静压密封结构的示意图如图1所示。

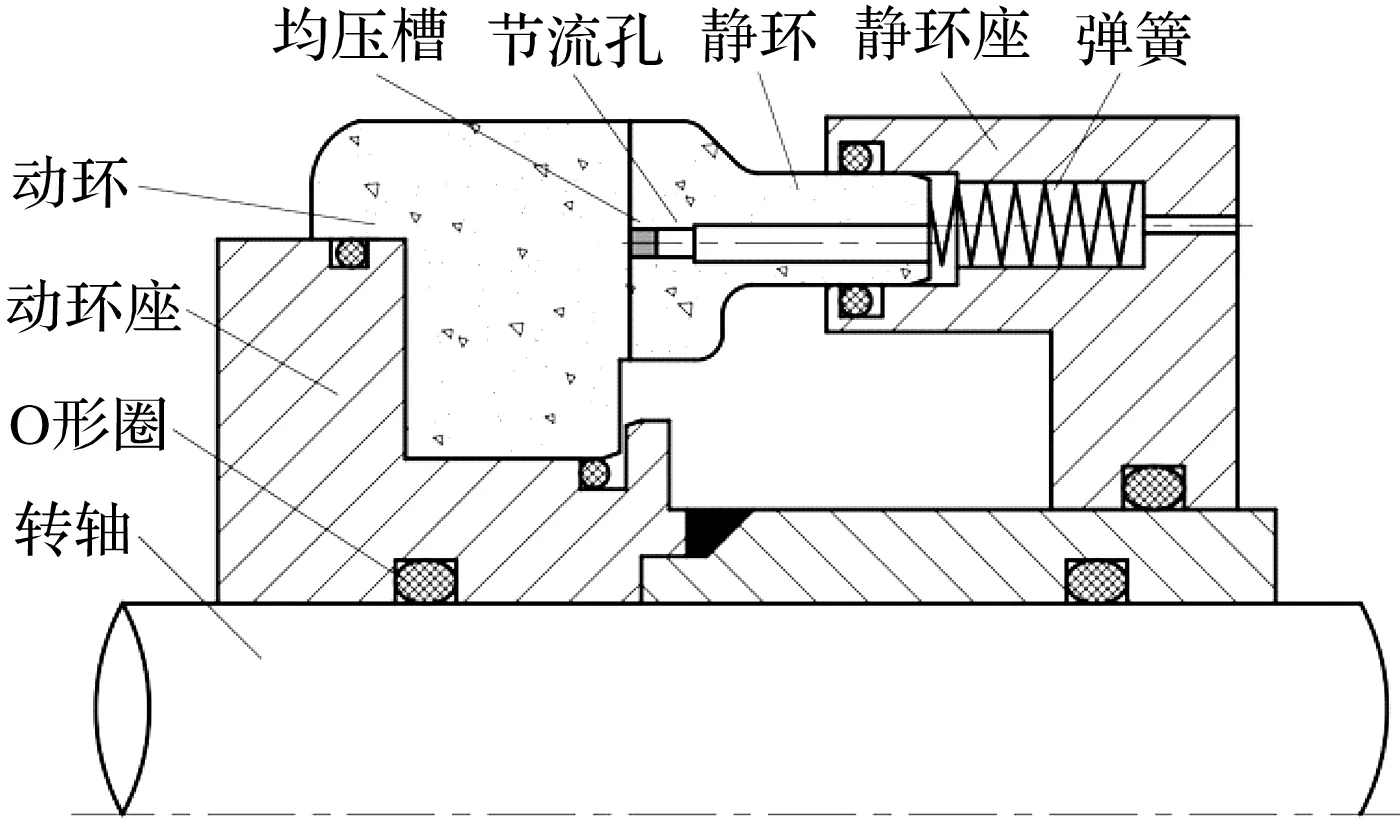
图1 可控型静压密封结构示意图

可控型静压密封主要由动环座、动环、静环座、静环、弹簧、O形圈、转轴等组成。通常采用的方法是将打孔的红宝石镶嵌在静环端面上,以此来获得静环节流孔。

可控型静压密封在工作状态下,密封气体进入静环座流道,首先,其作用在静环上侧面端面上,与弹簧共同形成闭合力;然后,在密封端面开启后,随着两密封端面的间隙逐渐增大,气体在密封端面形成的开启力逐渐下降;最后,直至开启力与闭合力平衡,密封端面形成一层微米级气膜,有效的静压密封得以形成。

由于可控型静压密封面由同一组密封气压调节,可以实现密封端面的可控调节,因此,其被称为可控型静压密封。

1.2 密封性能参数

1.2.1 内外泄漏量m

可控型静压密封的泄漏量m由内外泄漏量m1和m2构成[16],其可以利用两侧出口速度对出口面积分得到。具体的表达式如下:

m1=∬u1dsout1

(1)

m2=∬u2dsout2

(2)

式中:m1为内泄漏量,L/h;m2为外泄漏量,L/h;u1为计算流场内侧出口处横向速度,m/s;u2为计算流场外侧出口处横向速度,m/s;sout1为计算流场内侧出口面积,m2;sout2为计算流场外侧出口面积,m2。

1.2.2 气膜厚度δ

可控型静压密封气膜厚度与运行状态下的开启力相关。

在计算不同气膜厚度下的开启力后,笔者采用最小二乘法拟合气膜开启力,即关于气膜厚度的多项式[17],以获取不同开启力下的膜厚;再采用对应气膜面积下的压力积分,获得可控型静压密封开启力的大小。

其表达式如下:

Fopen=∬pds气膜

(3)

式中:Fopen为开启力,N;p为气膜压力,Pa;s为计算流场气膜面积,mm2。

1.2.3 气膜刚度K

气膜刚度[18]体现了可控型静压密封气膜对密封状态的动态响应程度,是反映密封性能的重要参数。

气膜刚度计算如下式所示:

(4)

式中:K为气膜刚度,N/m;δ为气膜厚度,μm。

2 密封计算模型及计算流程

2.1 计算模型

可控型静压密封端面的节流孔和均压槽是必不可少的结构。

节流孔可以控制气体流量,均压槽可以使气膜压力的分布更加均匀,同时起到二次节流的作用。可控型静压密封的均压槽具有多种形式。综合考虑加工和气压分布状态可知,典型的环形槽[19]具有最佳的槽型结构。因此,下面笔者采用环形槽进行研究。

环形槽结构如图2所示。

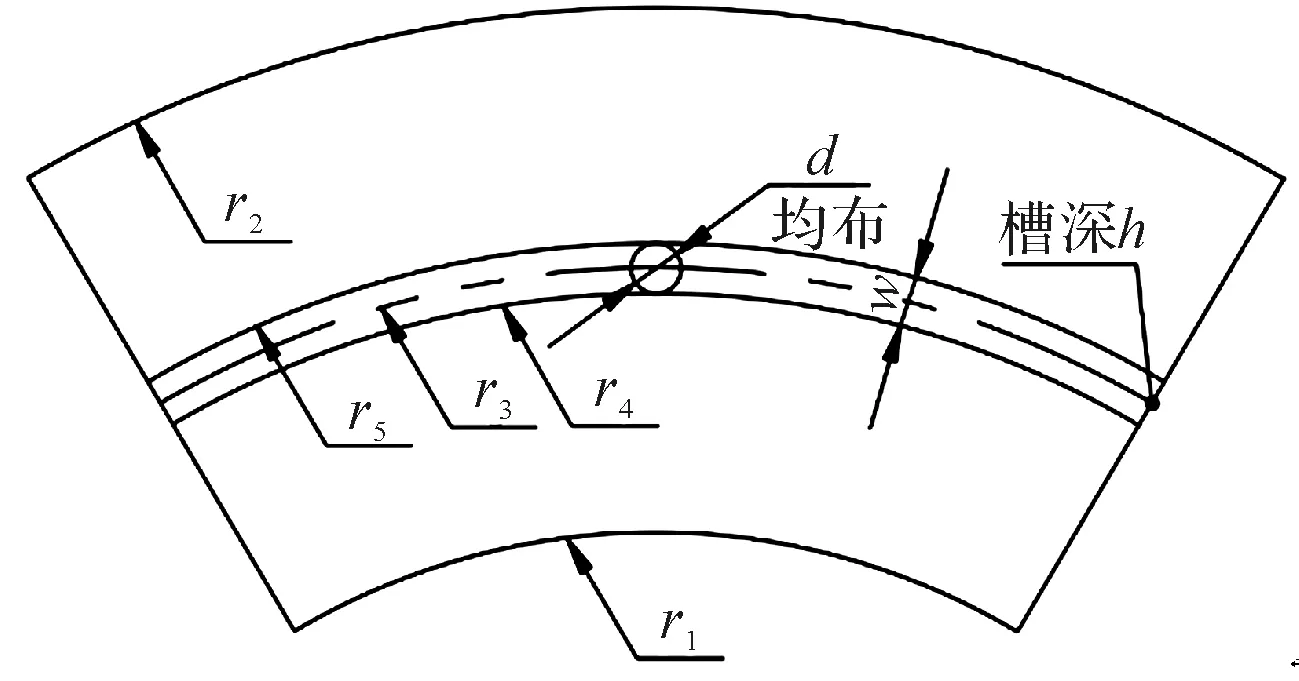
图2 环形槽结构

笔者的研究主要围绕可控型静压密封节流孔数量和直径尺寸、均压槽尺寸和位置、端面宽度3个方面对密封性能的影响而展开。

可控型静压密封结构参数如表1所示。

表1 可控型静压密封结构参数

可控型静压密封的性能参数分析对象为其端面的气膜流场。

可控型静压密封流场二维模型如图3所示。

图3 可控型静压密封流场二维模型

从图3中可以看出:密封气压力Pop经节流孔进入密封端面,形成开启力,产生端面气膜,使可控型静压密封端面分离;随着气膜流动密封气体沿密封端面向内外两侧泄漏,密封外侧泄漏流向被密封介质Pme,密封内侧泄漏流向大气环境Pair。

可控型静压密封工况参数如表2所示。

表2 可控型静压密封工况参数

2.2 边界条件和网格划分

2.2.1 边界条件

可控型静压密封的气膜面域较宽、厚度较薄,因此,采用层流模型进行数值模拟计算较为合适。节流孔上端面设置为流场入口,气膜内外泄漏出口为流场出口。可控型静压密封为中心对称的周期模型,笔者取1/6可控型静压密封模型作为研究对象,并在膜两侧设置周期性边界条件,其余设置为壁边界[20-23]。

2.2.2 网格无关性验证

为保证计算结果精确有效,提高仿真计算效率,笔者对模型网格进行了无关性验证。

网格无关性验证如图4所示。

图4 网格无关性验证

笔者以可控型静压密封开启力作为网格无关性验证判断依据。

在网格细化过程中,密封开启力先快速减少,随后趋于平稳。进行分析时,笔者选取网格单元数量为118 100个,网格节点数为206 200个,此时网格平均单元质量为0.98,仿真计算效果良好,证明了该模型计算的合理性。

2.3 计算流程

获取密封性能参数的仿真计算流程如图5所示。

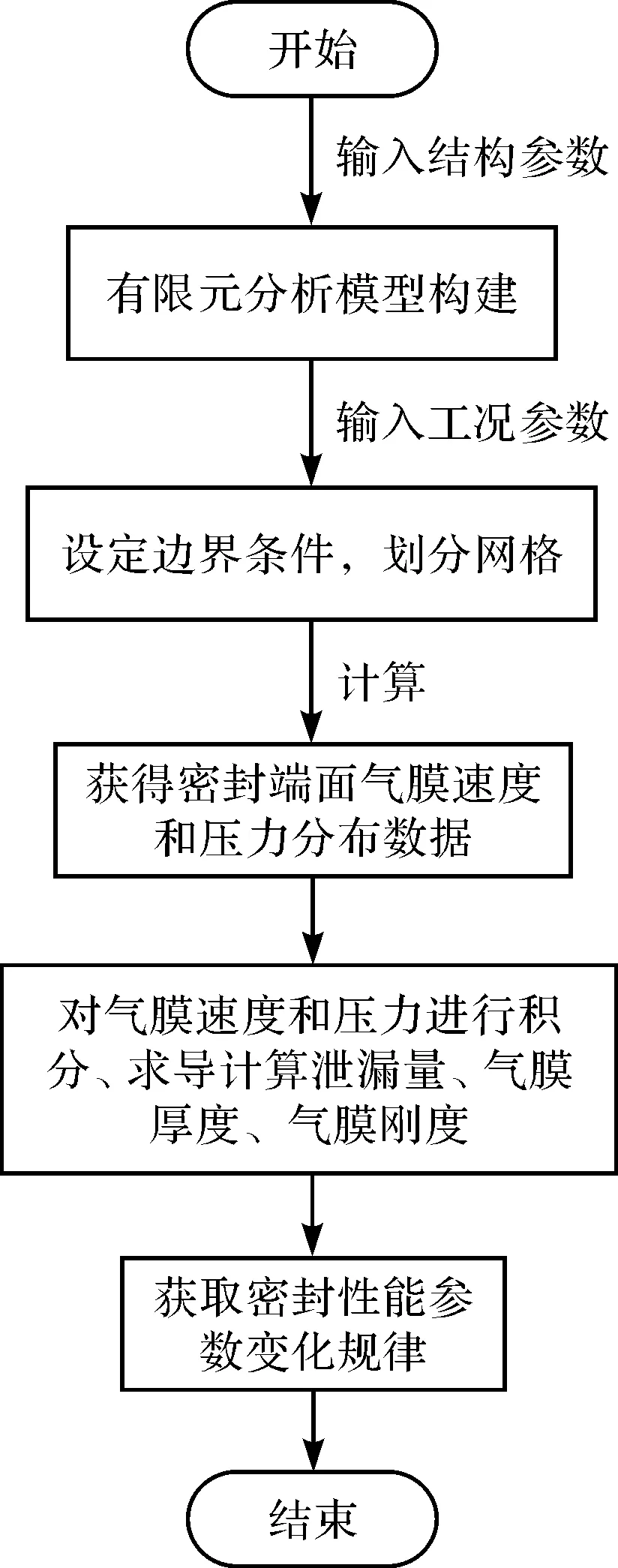
图5 仿真计算流程

3 计算结果

3.1 云图结果

通过计算获得可控型静压密封气膜压力与速度分布云图,如图6所示。

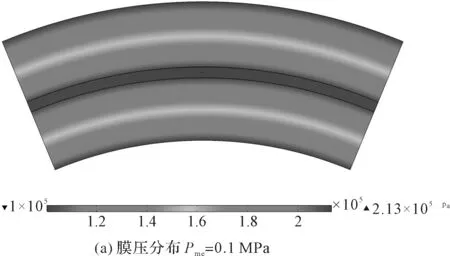
图6 可控型静压密封气膜压力与速度分布云图

1)从图6(a)和图6(c)中可以看出:均压槽处的气膜压力最大,沿着可控型静压密封端面直径矢量方向气膜压力逐渐降低;靠近密封侧时,气膜压力与外侧压力基本相同。当被密封介质无压时,均压槽两侧的气膜压力分布基本一致;当被密封介质压力高于大气压时,密封外侧承受更高的压力,此时靠近外侧的气膜高压区域较宽,而靠近内侧的气膜高压区域较窄。

2)从图6(b)和图6(d)中可以看出:速度分布也呈现相似的规律,气体沿节流孔进入气膜的过程中,气体在节流孔出口处产生较大的冲击作用,因此,在该位置形成了一个较大速度区域。

3.2 节流孔对密封性能影响

3.2.1 节流孔数量对密封性能影响

节流孔数量对可控型静压密封性能的影响如图7所示。

图7 节流孔数量对可控型静压密封性能的影响

1)根据图7(a)和图7(b)数据可以发现:相同密封气体压力下,节流孔数量的增加对于内外泄漏量和工作膜厚产生的影响较小。这是由于孔数增多时气流量增加,而密封气体压力不变,所以密封气膜压力不变。由此可见,密封端面气膜膜厚和内外泄漏量变化很小。

2)根据图7(c)数据可以发现:在不同密封气体压力下,随着节流孔数的增加,气膜的刚度迅速下降,当节流孔个数超出16个时,其气膜刚度逐渐趋于稳定。这是由于随着节流孔数增加,可控型静压密封气膜面积相应减少,导致密封端面开启力下降,气膜刚度会逐渐降低;节流孔数增长到一定数量时,形成的开启力与闭合力相等,此时气膜刚度稳定不变。

3.2.2 节流孔直径对密封性能影响

节流孔直径对可控型静压密封性能的影响如图8所示。

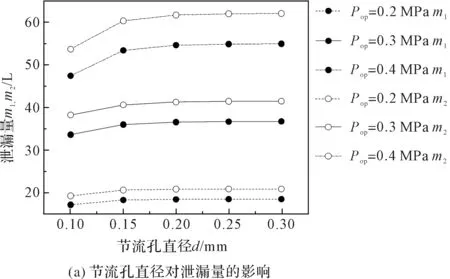
图8 节流孔直径对可控型静压密封性能的影响

1)根据图8(a)数据可以发现:随着节流孔直径的增加,气体通过节流孔的流速逐渐增大,泄漏量均有一定的增长;当到达直径0.15 mm后,泄漏量增加趋势逐渐放缓,基本维持不变。

2)根据图8(b)数据可以发现:在不同密封气体压力下,工作膜厚呈现先增加随后变为平缓的趋势。在Pop=0.4 MPa的工况下,当节流孔直径从0.1 mm～0.15 mm变化的增加过程中,工作膜厚增加了7.8%;当节流孔直径从0.15 mm～0.25 mm变化时,工作膜厚仅增加了1.8%。

3)根据图8(c)数据可以发现:气膜刚度呈现快速下降的趋势,当Pop=0.4 MPa时,节流孔直径从0.1 mm～0.3 mm的增加过程中,气膜刚度下降了98.5%。

综上所述:节流孔数在8个～12个,孔直径在0.15 mm～0.25 mm时,可控型静压密封的各项密封性能较好。

3.3 均压槽对密封性能影响

3.3.1 均压槽尺寸对密封性能影响

均压槽尺寸对可控型静压密封性能的影响如图9所示。

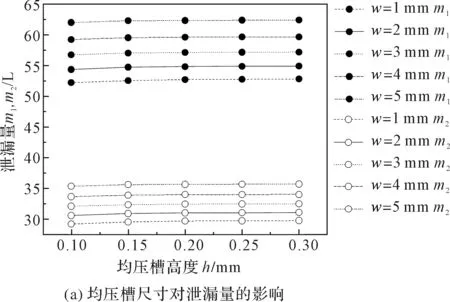
图9 均压槽尺寸对控型静压密封性能的影响

1)根据图9(a)和图9(b)数据可以发现:均压槽高度一定时,随着均压槽宽度的增加,可控型静压密封泄漏量和工作膜厚增大。这是因为均压槽宽度增加时,密封端面气膜面积增加,气膜体积增大,进入密封端面的气体量增大,导致内外泄漏量和工作膜厚都有一定增长。

2)根据图9(c)数据可以发现:在相同的均压槽高度下,气膜刚度随均压槽宽度的增加逐渐增大;相同均压槽宽度下,随均压槽高度的增加,气膜刚度逐渐降低。当均压槽高度h=0.3 mm时,均压槽宽度在1 mm～5 mm的增加过程中,气膜刚度增加了48%;均压槽宽度在w=5 mm时,均压槽高度在0.1 mm～0.5 mm的增加过程中,气膜刚度减少了37%。

3)以上结果表明:当均压槽高度一定时,均压槽越宽,气膜的承载能力就越好。

3.3.2 均压槽位置对密封性能影响

均压槽位置对可控型静压密封性能的影响如图10所示。

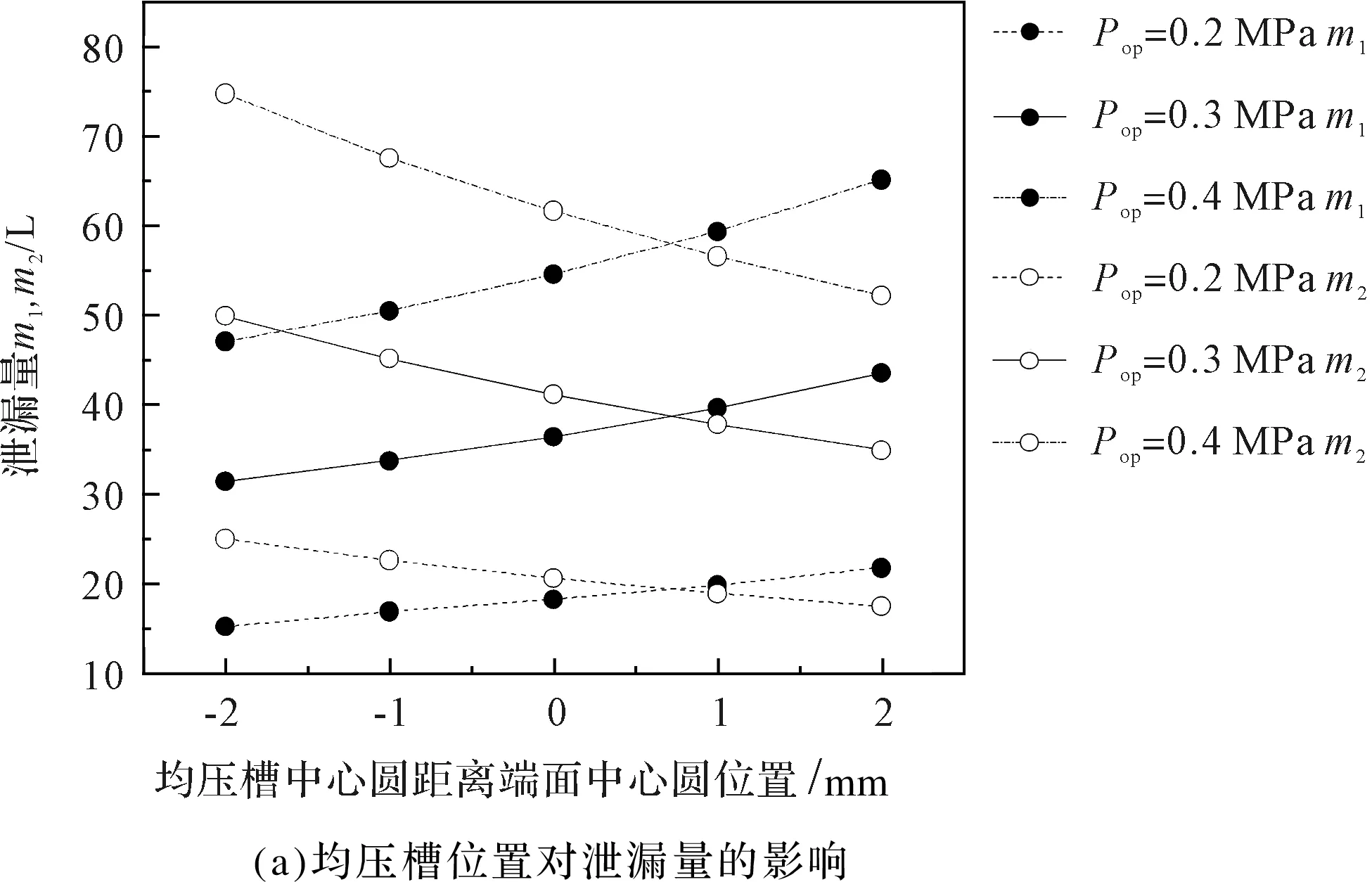
图10 均压槽位置对可控型静压密封性能的影响

笔者采用中心圆位置对均压槽的位置进行判断。其中,均压槽位置以均压槽中心圆与可控型静压密封端面中心圆的距离表示;以密封端面中心圆为基准点,靠近密封端面外侧规定为负,反之则为正。

1)根据图10(a)数据可以发现:均压槽位置由负到正的过程中,在不同密封气体压力下,泄漏量m1逐渐增大,泄漏量m2逐渐降低。

根据图10(b)数据可以以发现:当Pop=0.4 MPa时,均压槽位置从-1 mm～1 mm偏移的过程中,工作膜厚分别上升了0.031%和0.029%。

根据图10(c)数据可以发现:由于可控型静压密封端面面积不变,所以膜压分布总面积不变,膜压分布不受均压槽位置变化的影响,因此,气膜刚度基本保持不变。当Pop=0.4 MPa,在均压槽位置偏移2 mm的过程中,气膜刚度上下浮动不超过0.4%。

2)从图10(a)和图10(b)可以看出:均压槽位置距离密封端面内侧约0.5 mm处,内外泄漏量达到一致,并且此时两侧膜压分布几乎一致,可控型静压密封可以达到较好的密封性能。

3)综合分析可知:考虑密封性能和加工制造的难度,笔者选取均压槽宽度在2 mm～4 mm之间,均压槽高度在0.15 mm～0.25 mm之间,均压槽位置距离密封外侧约0.5 mm处,可控型静压密封可以展现较好的密封性能。

3.4 端面宽度对密封性能影响

端面宽度对可控型静压密封性能的影响如图11所示。

图11 端面宽度对可控型静压密封性能的影响

1)根据图11(a)和图11(b)数据可以发现:随着端面宽度的增加,内外侧泄漏量逐渐降低,工作膜厚呈线性减少。这是由于端面宽度的增加,会使气膜面积随之增加,可以承载的气体体积增大,两侧泄漏的气体和工作膜厚随之减少。当Pop=0.4 MPa时,端面宽度从21.5 mm～29.5 mm的增加过程中,工作膜厚下降了36%,内泄漏量下降了34%,外泄漏量下降了27%。

2)根据图11(c)数据可以发现:气膜刚度随端面宽度的增加略有下降。这是由于端面宽度的增加使可控型静压密封端面容纳更多气体,端面气膜膜压分布更加广泛,气膜承载能力提高,所以气膜刚度略有降低。

过大的端面宽度会使可控型静压密封整体结构增大,造成材料的浪费。因此,经综合考虑,密封端面宽度选择23 mm～27 mm较为合理,该范围的端面宽度既可以实现良好的密封性能,又降低了材料使用和加工成本,具有良好的适用性和经济性。

4 试验验证

为了对上述数值模拟结果的准确性进行验证,笔者搭建了试验台,并进行了装置的运转试验。试验内容主要是通过测量可控型静压密封的总泄漏量,以此来验证数值模拟的结果。

笔者自主设计了一套可控型静压密封试验装置。试验装置装配图如图12所示。

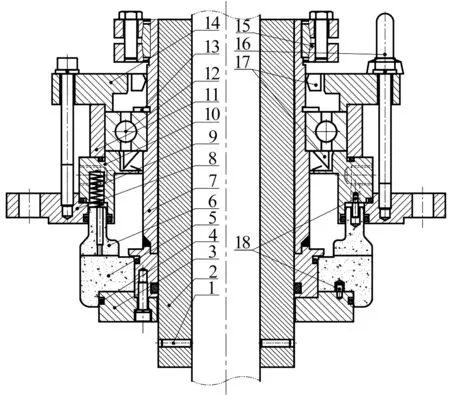
图12 试验装置装配图

在可控型静压密封装置中,动环与动环座、静环与静环座均通过防转销固定,静环座与机座相互联接,动环座与轴套通过螺栓相连。当静压密封装置运转时,轴套带动动环组件随轴一起转动,静环则保持相对静止。

试验装置实物如图13所示。

图13 试验装置实物

试验中,笔者设置电机转速n为1 200 r/min,被密封介质压力为0.2 MPa,密封气压力变化范围为0.2 MPa～0.4 MPa,测量可控型静压密封装置总泄漏量Q[24]的公式如下:

Q=m1+m2

(5)

泄漏量采用电显式流量采集器来测量,采集器实物图如图14所示。

图14 电显式流量采集器

该采集器所采集的数据能够精确到小数点后两位,且相对误差不超过5%。笔者将测量的数据记录在案,并将其与数值模拟数据进行对比。

数据对比结果图如图15所示。

图15 数据对比结果图

由图15可知:试验研究结果和数值分析结果与密封气体压力的变化趋势基本一致,且最大误差不超过6%。

试验运转数据结果表明了数值模拟分析结果的准确性和合理性。

5 结束语

针对可控型静压密封在恒定转速和被密封介质压力下的泄漏问题,笔者建立了可控型静压密封气膜流场模型,针对不同结构参数下的可控型静压密封性能进行了研究,揭示了结构参数对可控型静压密封的影响机理,获得了最佳的参数区间;最后,采用试验的方法对数值模拟结果的准确性进行了验证。

研究结论如下:

1)相比于数量,节流孔直径对可控型静压密封性能的影响更为显著,当节流孔个数在8个～12个,节流孔直径在0.15 mm～0.25 mm之间,可控型静压密封具有更好的密封性能;

2)均压槽高度对气膜刚度影响较大,随着均压槽高度的增加,气膜刚度迅速降低;在均压槽位置由负至正的过程中,内外泄漏量增长趋势相反,当其位置距离密封内侧约0.5 mm时,可控型静压密封的内外泄漏量达到一致,有效提升了装置的密封性能;

3)端面宽度的增加提高了气膜承载能力,可控型静压密封的整体密封性能获得优化,结合密封性能和成本因素,建议可控型静压密封端面宽度控制在23 mm～27 mm范围内为宜。

在后续工作中,笔者将针对可控型静压密封的运行稳态性能展开深入研究,以提高静压密封装置在运行状态下的密封性能。