面向冗余度机械臂多任务鲁棒控制的多层混合时变问题建模与求解

李艳灵,朱鑫辉,潘 爽,付志鹏,冯 岩

(信阳师范大学 计算机与信息技术学院, 河南 信阳 464000)

0 引言

冗余度机械臂控制广泛应用于工程救援、航空航天、医疗等领域[1],对机械臂控制算法的智能化要求也越来越高,不仅要有很好的实时性,而且要能有效执行多个任务,同时要求对复杂的控制环境具有很好的适应性。传统的控制算法(如PID控制、滑模控制)在理想环境下具有较好的性能[2]。这些传统控制方法在实时性、参数选取、鲁棒性等方面存在不足。

近年来,零化神经动力学方法被提出,并逐渐被学者熟知,该方法以时变的角度看待并描述问题,动态地解决问题,在实时性方面具有很好的特性。零化神经动力学方法用于机械臂控制时,具有很好的实时性。文献[3]将机械臂跟踪控制问题建模成时变西尔维斯特矩阵问题并求解,得到相应的控制算法;文献[4]将机械臂跟踪控制问题建模成二次规划问题。上述控制算法均有较好的实时特性,但是问题建模比较简单,只能完成单一的跟踪任务,不能完成其他额外任务,在复杂环境下也不具有鲁棒性。

针对多任务控制问题,研究者尝试将机械臂控制问题建模成多层结构时变问题,用不同的层描述不同的任务,在求解多层结构时变问题时同时实现多任务同时控制。文献[5]将控制问题建模成多层线性方程组问题,实现跟踪与姿态的同时控制;文献[6]将控制问题建模成多层时变问题,实现跟踪与关节角度极限的同时控制。多层结构建模方法很好地解决了多任务控制问题,但是在复杂环境下不具有鲁棒性。

针对以上问题,本文在多层时变问题建模的基础上,使用一种新的求解方法,在求解多层混合时变问题时构造积分形式的误差函数,并多次使用零化神经动力学公式,保证最终算法具有强鲁棒性。理论分析并数值实验验证在常量噪声、线性增长噪声、有界随机噪声3种环境下所提算法的鲁棒性,并与经典控制算法对比说明所提算法性能的优越性。

1 机械臂多任务控制问题建模

将冗余度机械臂多任务控制建模为多层混合时变问题。根据机械臂运动学方程可知,

f(θ(t))=ra(t),

(1)

式中:f(·)表示机械臂前向运动学映射函数;θ(t)表示机械臂关节角度向量,其在控制过程中随时间变化;ra(t)表示末端执行器实际轨迹。机械臂多任务控制中基本的跟踪任务是指实际轨迹ra(t)实时跟踪一条时变的期望路径rd(t),即ra(t)→rd(t)。因此,结合式(1),定义多层混合时变问题的第一层为

f(θ(t))=rd(t)。

(2)

显然,当控制过程趋于稳定时,式(2)能够满足,即可完成跟踪控制任务。

冗余度机械臂控制通常在完成跟踪任务的同时,还需要完成其他任务,比如受硬件约束而产生的关节角度极限、姿态控制、重复运动等。定义多层混合时变问题的第二层为

(3)

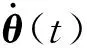
(4)

2 机械臂多任务鲁棒控制算法

2.1 控制算法的提出

为求解多层混合时变问题(4)并得到具有鲁棒性的控制算法,使用零化神经动力学方法将问题的第一层进行等价转化,进而与第二层合并以得到最终算法。等价转化过程如下:

将第一层时变问题的时间积分定义为第一个误差函数

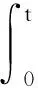
(5)

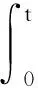
(6)

根据式(6),定义第二个误差函数

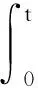
(7)

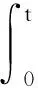
(8)

式中:J(θ(t))是f(θ(t))对θ(t)的偏导,为机械臂的雅可比矩阵。

将等价转化式(8)与多层混合时变问题(4)的第二层相结合得到

(9)

式中:

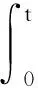
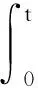
将上式代入式(9)得到如下微分方程形式的控制算法:

(10)

式中:

2.2 算法收敛性与鲁棒性分析

本文构建积分形式的误差函数,并多次使用设计公式,该方法是在零化神经动力学方法的框架下提升算法的鲁棒性。积分增强零化神经动力学是从控制论的角度,在设计公式中引入积分运算。两种方法的起源不同。此外,本文方法是积分增强方法参数择优选取的结果,积分增强方法中参数的选取直接影响最终算法的鲁棒性,而本文方法不需要调参就可保证鲁棒性。理论分析由以下定理给出。

定理1 从机械臂的有效初始位置起始,多任务控制算法(10)是指数收敛的,跟踪误差和附加任务执行误差趋于0,即

证明根据多任务控制算法(10)等效得到式(9),式(9)可拆分为式(8)和式(3)两部分,后一部分可使附加任务执行误差趋于0,即

定义跟踪误差向量函数

e(t)=f(θ(t))-rd(t),

根据式(8),考虑误差向量函数的某一个元素ei(t),则有

对上式整体求导得如下二阶齐次常微分方程

定理2 在多种噪声环境下,多任务控制算法(10)是鲁棒的,即在常量噪声环境下,误差指数收敛至0;在线性增长的无界噪声或有界随机噪声环境下,误差有界并且误差界随参数λ的增大而减小。

证明为分析控制算法(10)的鲁棒性,在算法中加入噪声n(t)。与定理1证明过程的前半部分类似,带有噪声符号的控制模型可推出

式中:ni(t)表示噪声向量的任一元素。接下来的证明过程分常量噪声n(t)=n、线性增长的无界噪声n(t)=nt、有界随机噪声n(t)三部分。

(1)常量噪声

当n(t)=n时,有

对上式整体求导得如下二阶齐次常微分

求解微分方程即证在常量噪声环境下,误差指数收敛至0。

(2)线性增长噪声

当n(t)=nt时,有

对上式整体求导并求解得

因此,在线性增长的无界噪声环境下,误差有界并且误差界随参数λ的增大而减小。

(3)有界随机噪声

当n(t)是有界随机噪声时,有

由文献[7]中引理3的证明过程可知,在有界随机噪声环境下,误差有界并且误差界随参数λ的增大而减小。证毕。

3 数值实验

以六连杆平面机械臂为例进行数值实验验证。机械臂的6个杆长均为1 m,随机定义机械臂的关节角向量θ(t)=(θ1(t),θ2(t),…,θ6(t))的初始状态为

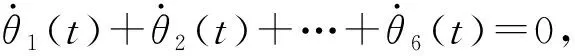
A(t)=[1,1,1,1,1,1],

B(t)=[0,0,0,0,0,0],C(t)=0。

控制算法在没有噪声环境下有效性的实验结果如图1所示。

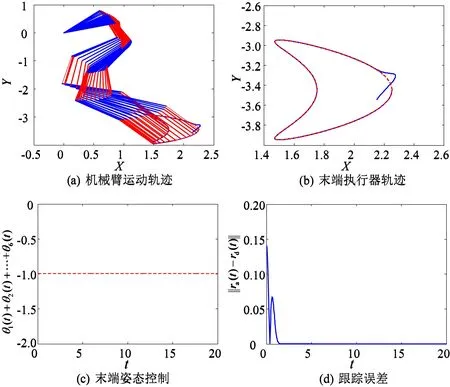
图1 无噪声环境下多任务控制算法有效性验证结果Fig. 1 Validation results of multi-task control algorithm without noises

根据图1(a)可以看出,最后一条杆的轨迹始终平行,实现了姿态控制。图1(b)展示的是末端执行器的实际运动轨迹以及期望路径对比,可以看出末端执行器的初始位置远离期望点,随着算法的执行,实际轨迹逐渐跟踪上了期望路径。图1(c)展示的是关节角度的累加和在控制过程中的变化情况,可以看出是始终保持不变的,进一步说明了姿态控制任务的有效完成。图1(d)展示的是跟踪误差,显然误差快速收敛至0,进一步说明了跟踪任务的有效完成。

经典的控制算法形式如下:

(11)

先后使用算法(10)和算法(11)在相同的实验环境下执行相同的任务,进行对比实验。实验结果如图2—图4所示,在3种噪声环境下,提出的算法均能很好地完成跟踪任务和末端姿态控制任务,而经典的算法不能完成这两个任务。

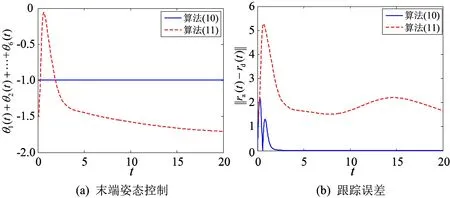
图2 常量噪声环境下本文算法和经典算法对比结果Fig. 2 Comparison results of the proposed algorithm and classical algorithm in the presence of constant noises

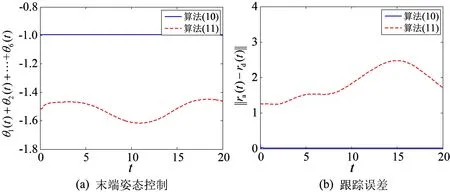
图3 线性增长噪声环境下本文算法和经典算法对比结果Fig. 3 Comparison results of the proposed algorithm and classical algorithm in the presence of linear-increasing noises

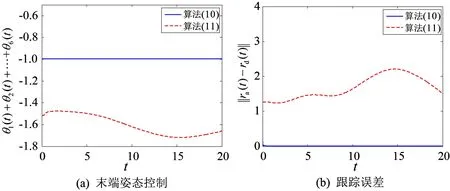
图4 有界随机噪声环境下本文算法和经典算法对比结果Fig. 4 Comparison results of algorithm the proposed algorithm and classical algorithm in bounded random noises

为验证在噪声环境下的控制精度与参数之间的关系,不同的参数值产生的误差如图5和图6所示,可见参数的增大能够提升精度。

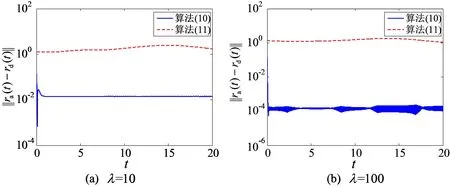
图6 有界随机噪声环境下不同参数取值误差精度对比Fig. 6 Comparison of accuracy by different parameter values in the presence of bounded random noises

4 结束语

在多层结构时变问题建模基础上,提出鲁棒控制算法,解决冗余度机械臂多任务控制中的噪声问题,所提出的算法可以实现实时跟踪任务和用户自定义的额外任务同时有效执行,并且在不同类型的噪声环境下均具有强鲁棒性。理论分析与数值实验均验证了所提算法的有效性和鲁棒性。