跨尺度网格识别方法及在防渗墙分析中的应用

余翔，赖远平，王钰轲，屈永倩，郑浩然

(1.中国地球物理学会工程物探检测重点实验室，湖北 武汉 430000；2.郑州大学 水利与土木工程学院，河南 郑州 450001；3.大连理工大学 水利工程学院，辽宁 大连 116024)

土石堤坝工程是我国重要的基础设施工程，为了保证设计的可靠性以及工程的安全性，常常会对工程结构的工作状态进行分析.网格剖分是有限元数值模拟的基础，因此网格尺寸大小对数值计算结果的可靠性和精确性影响很大[1].防渗墙作为控制堤坝渗漏的关键结构，是堤坝安全的控制部位.为了准确定位在不同运行条件下，防渗墙的薄弱部位会对防渗墙进行精细的网格剖分.防渗墙与堤体尺度跨越巨大，若按照均匀尺度的原则对堤坝工程进行网格剖分，防渗墙的小尺度网格尺寸标准将会造成数值模型具有大量自由度，计算量难以承受.相比于防渗墙，堤体的应力梯度一般较为平缓，常规尺度网格能够满足其精度要求.数值模拟对防渗墙的核心结构进行精细网格剖分，其它部分采用常规尺度网格剖分，获得了跨尺度网格，并引入数值计算方法，数值分析的计算量和精度均能够得到可靠保证.数值分析的计算量和精度同时得到保证是目前数值分析进一步推广应用的难题.

根据比例边界有限元法（scaled boundary finite element method, SBFEM）获得的网格单元对复杂几何边界适应能力强，具有实现跨尺度、精细化离散的特点.邹德高等[2-10]对比例边界有限元法进行发展和改进，取得了一定的成果.结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点，SBFEM-FEM 耦合求解分析逐渐发展起来.邹德高等[11-13]将该耦合法应用于结构应力分析，验证了该耦合法的可行性.殷德胜等[14-17]将耦合法应用于裂缝扩展和损伤破坏.Ye 等[18]将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解.目前SBFEM-FEM 跨尺度分析所采用的数值网格通常由四分树法获得.四分树法获得的网格单元形状固定、可控性差，无法适应土石堤坝中分层填筑和材料分区复杂的边界条件，难以根据实际情况相应做出合理的网格剖分方式，且可能造成需要精细模拟的部位会被忽略[19].

为了增强网格剖分的可控性，在CAD 软件中进行人为可控的网格划分，再识别并生成数值网格.李华等[20-22]提出二维有限元网格的识别和生成方法.田林等[23-27]在CAD 环境下，对二维网格生成方法进行改善优化，提高了网格的质量和生成效率.籍冉冉等[28]对莫尔斯（Morse）算法进行优化，提高了所生成的四边形网格质量.目前均是针对三角形和四边形单元的有限元数值网格，而有关非常规的多边形单元或SBFEM-FEM 耦合数值网格识别与生成的研究十分少见.

本研究结合CAD 人为可控的特点，对图形线段进行预处理，生成有效节点与线段，根据所生成的节点和线段之间的拓扑关系及封闭域构造，构建可以直接用于数值分析的网格模型，以及二维SBFEM-FEM 耦合网格生成方法.本研究将跨尺度网格识别方法应用于某实际堤坝工程的数值分析研究中，验证了网格生成方法获得的SBFEM-FEM 耦合网格的有效性和精度.

1 SBFEM-FEM 耦合分析方法

比例边界有限元法是由Wolf 等[29-30]提出，该方法在边界处利用Galerkin 方法进行数值离散，降低了一个空间的计算维度，可以在边界内部不需要基本了解的情况下利用解析的方法求解.比例边界有限元法不仅具有较高的精度，而且对单元形状的容许度更高，不需要根据单元的结点数量开发相应单元类型，突破了常规有限元法的限制.图1 为典型的多边形比例边界单元，图中ξ 为单元径向坐标，s为环向坐标.

图1 比例边界有限元法中的边界离散单元Fig.1 Boundary discrete element in scaled boundary finite element method

对于任意一个扇形区，通过边界积分点和特征值分解技术可求得单元形函数和应变位移转换矩阵：

式中： Ψu为位移模式对应的转换矩阵，可以通过特征值分解求得；Sn为特征值分解获得的特征值矩阵；n为单元边数；B(·) 为应变-位移的转换矩阵；I为单位矩阵.通过采用有限元的原理以及域内积分点，即可求出单元刚度矩阵：

式中：Kep为弹塑性刚度矩阵，Dep为弹塑性本构矩阵，F为每个高斯点所代表的面积，Rint为内力向量，σ 为单元应力场，ε 为应变.

通过网格跨尺度剖分，实现对核心结构网格加密，通常需要用多级过渡，如图2（a）所示.单元尺寸过渡中必然会引起5 节点及以上节点数目的单元，而这类单元需要单独构造形函数、积分方法，计算较为麻烦.不需要根据单元的结点数量开发相应单元类型是比例边界有限元法的一个特点，网格跨尺度通过一级比例边界有限单元就可以过渡完成，如图2（b）所示.过渡单元两侧采用有限单元模拟，且采用本研究方法进行网格任意加密，有效地解决了复杂几何区域的网格剖分.

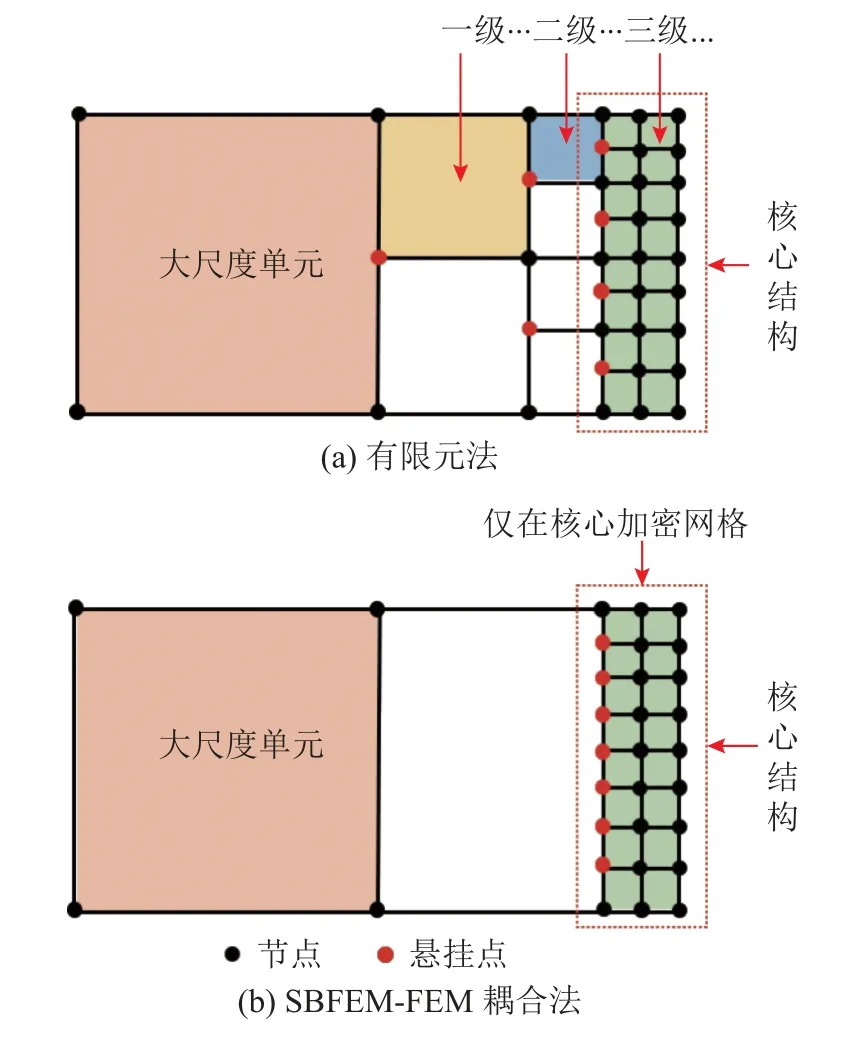
图2 跨尺度网格过渡方法的示意图Fig.2 Schematic diagram of cross-scale mesh transition method

2 SBFEM-FEM 耦合网格生成方法

2.1 CAD 数据处理

本研究提出的SBFEM-FEM 耦合网格生成方法主要分3 步：处理CAD 数据；对节点和线段信息预处理；生成数值网格信息.以下结合图3 所示的结构，说明耦合网格的生成方法.

图3 悬臂梁结构的示意图Fig.3 Schematic diagram of cantilever beam structure

在CAD 软件中，根据模拟对象创建节点与线段.在CAD 中绘出结构的二维简化图形，如图4所示.提取图中6 条线段、12 个节点的信息，作进一步处理.首先求解线段的交点，并将线段在交点处裁剪为多个子线段；判断节点的公用次数，若公用次数不大于1，则该节点无效，且该节点所属线段也无效；最后对所有有效节点和线段重新进行排序生成基本网格，并存储节点和线段信息如图5 所示.

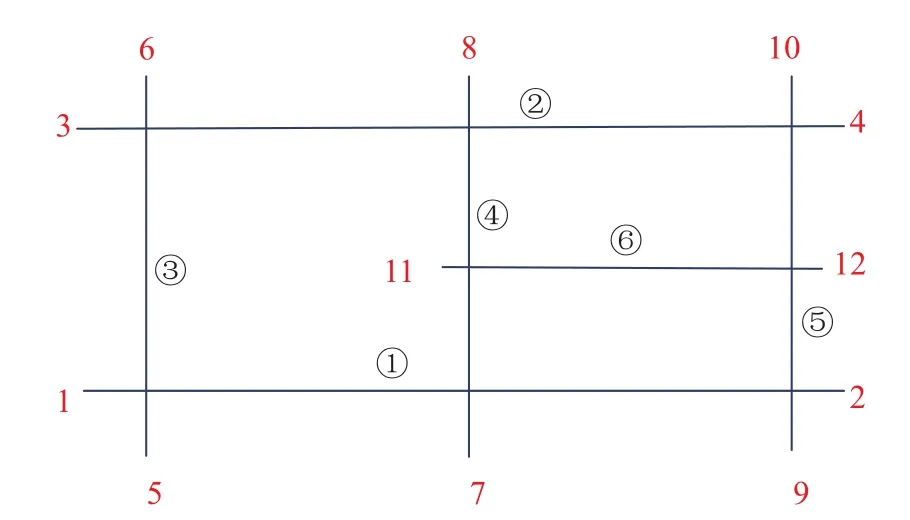
图4 悬臂梁结构的简化示意图Fig.4 Simplified schematic diagram of cantilever beam structure

2.2 节点与线段信息预处理

1）创建节点对称矩阵A，如表1 所示.通过节点关系矩阵A快速确定节点之间的连接关系，相应的节点连接关系，如图6 所示.若是A(i,j)=1 ，则i节点和j节点可组成ij线段.矩阵A的上三角矩阵中值为1 的个数是整个网格中的线段数量，应与上一步所识别出的有效线段数量相等.

2）创建单个节点连接向量VNL，如表2 所示.VNL(i)用于存储矩阵A的上三角矩阵第i行中值为1 的个数.

表2 节点连接的数目Tab.2 Number of node connections vector

3）处理共用某一节点的所有线段.创建3 个向量NLN、NLC 与NLA，分别存储共用节点线段的编号、在相应共用线段中的节点排序（值为1 或2）以及以节点为基准的线段与向量(1,0)的夹角，并根据NLA 由小到大将这些线段进行逆时针排序.

2.3 数值网格信息生成

2.3.1 遍历有效节点 1）根据节点编号顺序，依次判别.当节点编号为a时，判别 VNL(a) 大小（VNL(a)为矩阵A的上三角矩阵第a行中值为1 的个数），若 VNL(a)≥2 ，则该节点可生成新单元，否则不可生成，且进行下一节点的判别.以图7 为例，判别出节点a可以生成新单元，则进入第2.3.2 节遍历共用当前节点的线段.2）当所有节点遍历结束，则网格识别完成.

图7 单元生成的判别方法及流程Fig.7 Identification method and process of unit generation

2.3.2 遍历共用当前节点的线段 1）识别共用节点的线段，并确定过渡点.每相邻的2 条线段(NLN(i+1)与 N LN(i) )为一组，其中必有 N LA(i+1)>NLA(i).确定过渡点后进入第2.3.3 步.2）所有相邻共用线段遍历结束，则回至2.3.1 步中第1）步重新判别下一个节点的VNL 值大小.

以共用节点a的线段为例，若单元有n个节点，则节点a为单元的起始点，即第1 个节点.线段NLN(i+1)为单元的终结边，该线段另一节点b 为单元的终结点，即第n个节点；线段 NLN(i) 为单元的起始边，该线段另一节点m为单元的过渡点.

2.3.3 判别过渡点与终结点的连接关系 1）若过渡点与终结点可连成线段，即A(i+j)=1 ，则新单元生成，回至第2.3.2 节判断共用节点的下一组线段.2）若A(i+j)≠1 ，则该过渡点为单元中间点，继续寻找下一个过渡点.3）顺序循环执行本步第1）、2）步.

以上述共用节点a为例，若是A(b,m)=1 ，则组成单元a-m-b；若是A(b,m)≠1 ，则m组成新单元的中间点，记录该节点并继续查找组成单元的第n-1 个节点.查询共用节点m的所有线段，确定线段NLN(i)在共用节点m的所有线段中的排序j，基于组成单元的所有节点须逆时针排序的原则，定位线段 NLN(j-1) ，获得与节点m共同组成线段NLN(j-1)的另一节点，该节点为此时的过渡节点m，然后继续判别A(b,m) 是否等于1.该例最终生成单元a-m1-m2-m3-b.

用上述方法将图3 所示结构划分为用于数值分析的网格，如图8 所示.单元尺寸为在CAD 软件中所画线段的实际长度，通过所提方法的识别节点和线段直接确定单元尺寸，材料区域的数量对网格的识别无任何影响.在网格识别成功后，根据材料分区线、填筑分层线以及界面位置等控制信息自动完成材料区域的划分，接触单元生成计算分析前的关键步骤.

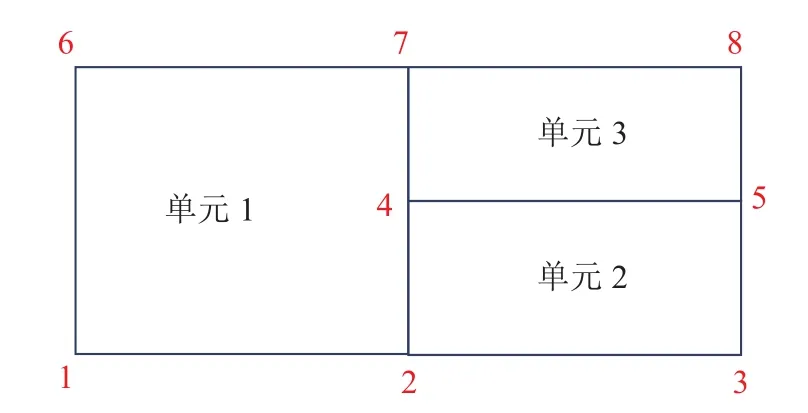
图8 最终识别出的悬臂梁结构的跨尺度网格Fig.8 Cross-scale mesh of cantilever beam structure of final identification

3 应用案例及分析

某堤坝位于河南省信阳市罗山县，是以防洪、灌溉为主的小（1）型水库.该水库工程等级为第Ⅳ级，主要建筑物为4 级.该水库主坝为均质土质堤坝，坝基由重粉质壤土、细砂及云母石英片岩组成.坝基土体渗透系数为1.6×10-6∼8.9×10-5cm/s ，平均渗透系数为 2.6×10-5cm/s ，具有微弱的透水性，在堤坝轴线剖位采用混凝土构筑悬挂式防渗墙进行防渗.

3.1 计算模型

图9 为工程的二维模型，X为顺河向，Y为高程方向.坝高15.00 m，坝顶宽5.60 m，坝底宽89.66 m.上游坡比1∶2.73 和1∶2.58，混凝土防渗墙位于坝体的中部，高17 m，嵌入坝基 2 m ，厚度50 cm.坝基高20 m，基岩高2 m，坝基、基岩总水平长度290 m.坝体分层填筑和蓄水模拟共分为29 个荷载步：

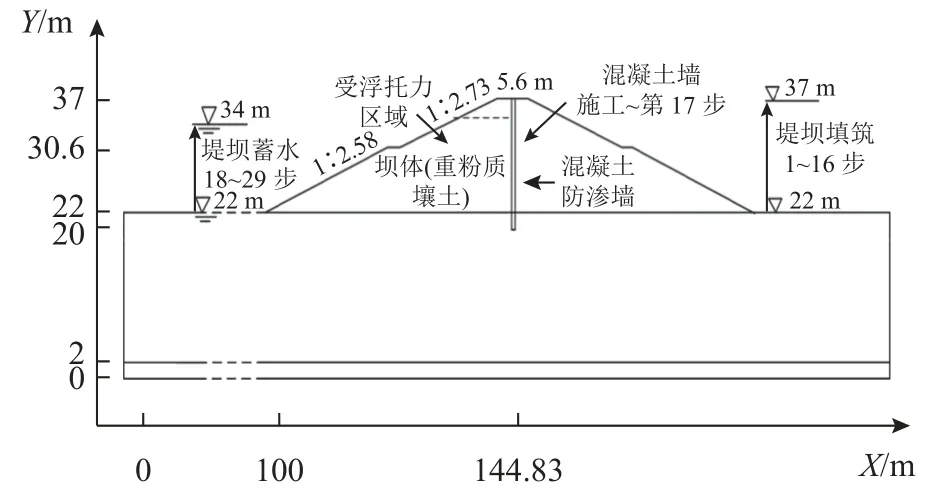
图9 堤坝的材料分布及荷载步的示意图Fig.9 Sketch of material distribution and load steps of embankment

1）分16 步（地基作为初始应力）对坝体从坝基面（高程22 m）填筑至坝顶（高程37 m），墙体材料按土体进行计算；2）第17 步将墙体位置的土体换成混凝土材料进行计算；3）再分12 步从坝基面蓄水至坝顶.其中，蓄水引起的静水压力以面力的形式施加于防渗墙的上游面与下游面（嵌入坝基部分），如图10 所示.

图10 堤坝防渗系统受力示意图Fig.10 Schematic diagram of force on anti-seepage system

3.2 材料参数

堤坝体与堤坝基的静力分析了采用邓肯-张E-B 非线性模型[31]，坝体、坝基材料参数取自实际试验结果[32].参数如表3 所示.其中 γd、 γf分别为干重度和浮重度；c、φ和 ∆φ分别为凝聚力、摩擦角和摩擦角随围压增大10 倍的减小量，三者均为强度参数；k和 β 分别为弹性模量系数和指数；Rf为破坏比；kb和q分别为体积模量系数和指数参数；kur和nur分别为卸载模量系数和指数.

表3 坝体和坝基的静力参数Tab.3 Static parameters of dam body and foundation

混凝土防渗墙和基岩材料均采用线弹性本构模型计算，材料参数如表4 所示，其中 ρ 为密度、E为弹性模量、 ν 为泊松比.

表4 墙、基岩的静力参数Tab.4 Static parameters of wall and bedrock

采用Goodman 接触单元模拟墙与土之间的接触面，用Clough-Duncan 双曲线模型[33]表达其应力-应变关系，该模型认为单元切向应力与切向相对位移之间的关系呈双曲线关系.则切向刚度为

式中：τ 为切向刚度，ω 为应变力，u为实验参数，K、Rf和j为非线性参数，δ 为接触面的界面摩擦角，γw为水的重度，P为大气压，σn为法向应力.

董景刚[34]对接触面单元的法向刚度应取值为相邻材料弹性模量的50～100 倍，接触面模型的法向刚度与切向刚度的关系大致为.法向刚度 = ， 是50 倍的混凝土弹性模量.初始切向刚度= ，是法向刚度的0.4 倍.接触面材料参数取自实际试验结果[35]参数如表5 所示.

表5 接触面的静力参数Tab.5 Static parameters of contact surface

3.3 计算网格模型及验证

为了验证本研究数值网格生成方法的有效性以及SBFEM-FEM 耦合数值网格的精度，分别根据以下3 种情况剖分堤坝模型，并采用本研究建立的方法进行数值网格的生成.堤坝主体耦合网格剖分图和网格剖分细图如图11 所示.模型1：大尺度常规单元网格（墙体单元竖向长度与土体单元保持一致）.模型2：耦合的SBFEM-FEM 单元网格（只在墙体进行局部加密，土体单元与模型1 一致）.模型3：精细尺寸常规单元网格（以模型2 中墙体单元尺寸为基准，均匀剖分堤坝）.

图11 墙体与土体局部单元示意图Fig.11 Diagram of local elements of wall and soil

图12 为模型2 耦合SBFEM-FEM 网格通过本研究方法识别生成的有限元模型局部网格示意图.其中，常规单元单元类型号为1、多边形单元单元类型号为44、接触单元单元类型号为4 表示.可以看出，图12 与图11（b）完全一致，表明了本研究建立的数值网格生成方法的有效性.

图12 耦合SBFEM-FEM 网格识别后的单元分布Fig.12 Coupling SBFEM-FEM mesh after mesh recognition

表6 和图13 为3 种网格下堤坝节点、单元信息和墙体单元信息，其中N*为节点总数量，N为模型总单元数量，n*为防渗墙单元数量，M为模型编号，H1和H2分别为墙体竖向和横向长度.模型2 耦合SBFEM-FEM 网格单元数量与模型1 相差很小，而墙体单元数量是模型1 的3.8 倍.模型2墙体单元数量与模型3 墙体单元数量相等，而总单元数量是模型3 的约1/3.

表6 节点、单元的信息Tab.6 Information of node and unit

图13 3 种模型下堤坝单元和墙体的单元数量Fig.13 Element number of dam and wall for three conditions

本软件生成的计算模型采用大连理工大学抗震研究所自主研发的大型岩土工程静、动力非线性分析软件GEODYNA 进行数值计算.图14 为堤坝蓄水完成后，3 种模型下堤体的水平、竖向位移.可以看出网格对堤坝的整体变形结果影响很小，3 种模型下的变形等值线基本吻合.当研究堤坝整体变形分布规律时，常规有限元模拟及分析方法也能获得较高的精度.

图14 蓄水后堤体的位移分布图Fig.14 Distribution of dam displacement after impoundment

图15 为蓄水后墙体的水平位移.图中 ∆S为水平位移，H为墙体竖向高程.从图15 可以看出，墙体位移分布规律没有变化.墙体最大位移出现在墙顶，墙体最大位移为7.3 cm，这是蓄水后上游水压力及上游堤体浮托力共同作用的结果.防渗墙位于堤坝中部，其变形完全受堤体控制，墙体变形对单元尺寸不敏感.当研究堤坝防渗墙变形规律时，采用单元尺寸较大的大尺度网格模拟.

图15 蓄水后墙体的水平位移示意图Fig.15 Horizontal displacement of wall after impoundment

图16～18 为蓄水后墙体上、下游侧和蓄水后堤坝体（不含防渗墙）最大、最小主应力分布曲线.图中 σ1为 最大主应力， σ3为最小主应力.从图16～18可以看出，3 种网格获得的应力分布规律相同，但大尺度常规网格的计算结果与其它2 种差别较大，本研究耦合SBFEM-FEM 网格的计算结果与精细常规网格计算结果相差甚微.大尺度常规网格计算结果低估了墙体峰值，其计算结果不能作为评价墙体安全性能的依据.

图16 蓄水后墙体上游面的最大、最小的主应力分布图Fig.16 Maximum and minimum principal stress distribution of wall in upstream after impoundment

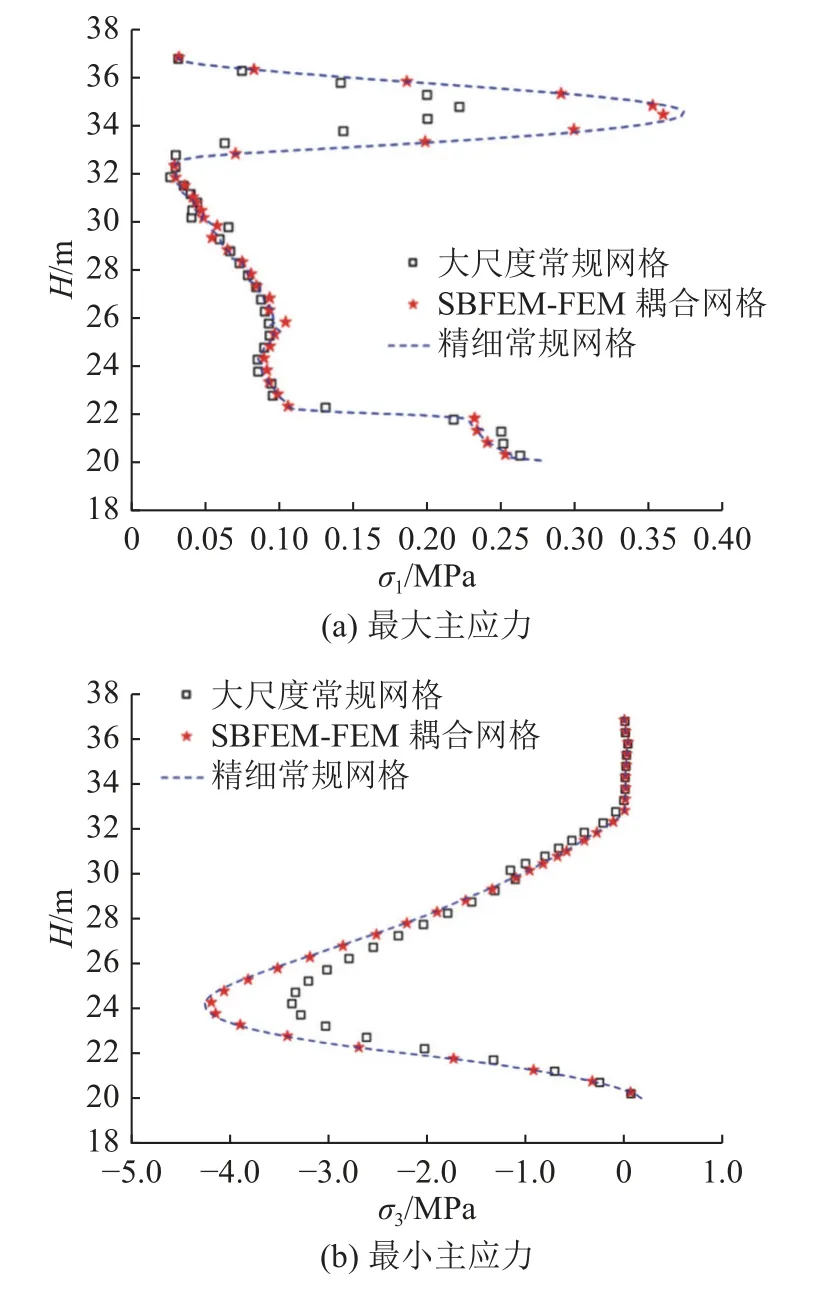
图17 蓄水后墙体下游面的最大、最小主应力分布图Fig.17 Maximum and minimum principal stress distribution of wall in downstream after impoundment

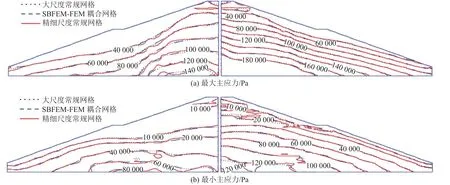
图18 蓄水后堤坝的最大、最小主应力分布图Fig.18 Maximum and minimum principal stress distribution of embankment in downstream after impoundment

表7 为蓄水后防渗墙主应力的峰值.其中F为峰值，以压应力为正，拉应力为负；D为误差.与精细网格相比，大尺度网格获得的墙体大主应力误差可以达到29.5%，小主应力误差接近50%，而耦合网格的误差均小于5%.耦合SBFEMFEM 模拟与分析方法可用少量网格获得较高精度的结果.

表7 3 种模型下墙体的主应力Tab.7 Principal stress of wall for three conditions

4 结 论

（1）对于堤坝工程，可以采用常规大尺度有限元网格分析堤体整体变形规律以及堤坝中部防渗墙的变形规律.当研究防渗墙应力特性时，防渗墙须采用精细网格剖分.与常规精细化有限元网格的结果相比，常规大尺度有限元网格模拟获得主应力的误差可以超过48%.

（2）基于SBFEM-FEM 耦合数值网格的数值模拟，计算效率及精度均较高.SBFEM-FEM 耦合数值模拟分析融合了SBFEM 的灵活通用性以及FEM 求解高效的特点，简便地完成了大尺度堤体有限元网格与精细墙体有限元网格的过渡.相应跨尺度数值网格获得的墙体应力与常规精细化有限元网格的结果相比，误差不超过5%，而跨尺度数值网格单元量大幅度降低.