四足机器人“盲爬”阶梯策略设计与实现

罗 荣,钱乐天,罗 欣

(华中科技大学机械科学与工程学院,湖北 武汉 430074)

0 引言

现有的四足机器人爬阶梯方法多为“显爬”方式,即预先设定或采用视觉传感器获取阶梯地形先验信息,据此合理地规划机身姿态和摆动腿足端轨迹[1-3]。但这种方式完全依赖于先验地形信息,在某些场景下难以发挥作用,如有烟、雾、霾或是处于山洞、夜间等视觉传感器难以获取地形信息的环境。

“盲爬”作为“显爬”方式的重要补充,逐渐得到研究者的重视[4-5]。“盲爬”没有先验地形知识,只能通过机器人内部感受器和触觉信息的融合后验估计局部地形,据此调整机身姿态。“盲爬”过程中摆动腿不可避免地与阶梯台阶发生磕碰。因此,机器人需要具备高动态稳定性和意外磕碰事件处理能力。

在爬阶梯运动规划方面,现有爬阶梯方法大多采用基于零力矩点的静步态规划方法[6-7],使零力矩点始终位于机器人支撑多边形范围内。黄博等[8]利用运动空间需求最小、稳定裕度最大和步态协调性最好等评价指标,对四足机器人的基本步态进行了对比分析,提出了基于投影分析法结合平面静平衡步态理论的阶梯步态规划方法。Lee等[9]在静步态规划基础上,控制足地接触力对质心产生的角动量变化率最小,降低了机器人在阶梯上倾斜的可能性。Ye等[10]分析并确定了机器人阶梯上不同支撑腿配置情况下的最优机身姿态,设计了最优姿态之间的转换策略,以使机器人能够安全地攀爬阶梯。总体上看,由于基于零力矩点的静态阶梯运动规划方法要求时时处处保持静平衡,攀爬速度慢,动态稳定性较差,尤其难以应对“盲爬”方式存在的机器人腿与阶梯台阶竖直面磕碰的问题。

本文设计了一种四足机器人采用对角小跑步态快速“盲爬”阶梯策略。根据触地腿实时估计阶梯局部信息;基于贝塞尔曲线设计了针对阶梯地形的摆动腿足端轨迹;基于广义动量法设计了对于摆动腿足端磕碰阶梯台阶竖直面的检测方法,并对磕碰问题进行了处理;基于稳定裕度概念以及估计的阶梯部分尺寸参数实时规划机身的参考轨迹,采用模型预测算法对参考轨迹进行跟踪,保证机器人快速稳定地“盲爬”阶梯。通过实验验证了策略的正确性。

1 阶梯信息估计

定义阶梯每步台阶纵向方向尺寸为台阶深度d,竖直方向尺寸为台阶高度h。由于宽度方向与机器人攀爬方向垂直,故不需要考虑。定义机器人前后支撑腿足端连线与水平面形成的“虚拟坡度”角度为β,并视为阶梯的“局部坡度”,如图1所示。为便于描述,在水平面定义世界坐标系{D},其ZD轴竖直向上。于机身质心处定义机身坐标系{B}原点,其XB轴与机身躯干平行,ZB轴垂直机体向上,YB轴符合右手定则。

设定机器人攀爬步态为对角小跑步态,某时刻前后支撑腿分别位于上下级台阶时,β为

(1)

lt为前后支撑腿足端在世界坐标系水平面投影距离;ht为竖直方向上的距离,作为估计的台阶高度。其表达式为:

lt=lcosθ+Δxbk+Δxfj

(2)

ht=Δzbk-Δh

(3)

l为机身长度尺寸;θ可通过惯性测量单元测得;j、k∈{L,R}为左、右;Δh为后支撑腿髋关节转轴与前支撑腿足端在世界坐标系竖直方向上的距离,即

Δh=Δzfj-lsinθ

(4)

Δxfj和Δxbk分别为前后支撑腿的髋关节转轴到足端矢量lg在世界坐标系x方向投影;Δzfj和Δzbk分别为相应的z方向投影。lg可通过腿部运动学求出。

2 运动规划

2.1 摆动腿规划

2.1.1 落足点规划

机器人摆动腿i期望落足点在世界坐标系X-Y平面投影位置pi,e,x-y∈R2通过线性组合公式确定,即

(5)

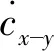
pi,h,d,x-y=cx-y+pi,h,c,x-y

(6)

cx-y∈R2,为机身质心实际位置在世界坐标系X-Y平面的投影;pi,h,c,x-y∈R2,为摆动腿i髋关节相对于机身质心位置在世界坐标系X-Y平面的投影。

摆动腿i足端在世界坐标系的期望摆动高度zi为

zi=zi,0+(ht+Δh)

(7)

zi,0为摆动腿i足端在世界坐标系的实际高度;Δh为在估计的台阶高度ht基础上增加的余量。

2.1.2 足端轨迹规划

为减小足端与阶梯台阶竖直面发生磕碰的概率,本文基于多控制点的贝塞尔曲线设计了一种针对阶梯地形的足端轨迹,如图2所示。

图2 基于贝塞尔曲线的足端轨迹

图2中x和z向的长度被归一化处理,虚线为各控制点连线,共7个控制点,实线为生成的足端轨迹。n控制点的贝塞尔曲线P(t)可由以下递推公式求出,即

(8)

其中,Bi,n(t)为

(9)

为减小摆动腿因提前触地受到的地面反力对机器人稳定性的影响,当某腿检测到足地接触事件时,控制该腿不再进行后续的摆动。

2.1.3 磕碰检测与处理

如图3所示为摆动腿足端磕碰阶梯台阶竖直面。由于传统的力估计方法噪声大,本文基于广义动量法[13]检测足端磕碰事件。

图3 摆动腿足端磕碰阶梯台阶示意

关节开链机械臂与环境产生碰撞时,动力学为

(10)

(11)

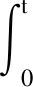
(12)

r为观测的外力矩值;K是增益对角矩阵;pest为满足式(11)的动量估计值,结合式(11)、式(12)得

(13)

机器人单腿可视为多关节机械臂,由于碰撞冲击对膝关节动量的影响最大,只考虑膝关节的动量变化,检测算法离散形式为

(14)

若抬脚过程发生磕碰,将足端x向的期望位置pi,e,x设为当前实际位置,当足摆到期望的最高位置后,继续跟随原规划点摆动;若落脚过程发生磕碰,将所有摆动腿足端在世界坐标系x向的期望位置pe,x设为

pe,x=px+Δx

(15)

px为摆动腿当前实际位置;Δx为调整值,以减小下一次摆动发生磕碰的概率。

2.2 机身规划

稳定裕度越大机器人越稳定,稳定裕度可以通过机身质心位置离零力矩点(ZMP)的距离判定[15]。四足机器人以动步态如对角小跑步态运动时,稳定裕度可视为机身质心与1对支撑腿足端连线的距离。为使稳定裕度最大,机身质心的期望水平位置应尽量靠近连线中点。另一方面,为了快速高效地攀爬阶梯,机器人水平速度应尽量维持在设定的恒定速度值附近。综合以上2个需求,机身水平参考速度的计算描述为

(16)

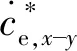
(17)

|ct,x-y-(pf,e,x-y-pb,e,x-y)/2|≤δc

(18)

pf,e,x-y和pb,e,x-y分别为通过式(5)得出的前后支撑腿足端期望位置水平投影;δc为设定阈值。

机身质心竖直方向期望位置参考前后支撑腿为

(19)

ce,z为质心竖直方向期望位置;zc为根据机器人尺寸预设恒定值;pf,z和pb,z为前后支撑腿竖直方向实际位置。

对于台阶高度相比机器人尺寸不高的阶梯,机身保持水平更有利于攀爬[16]。依据阶梯“局部坡度”β和台阶高度ht,机身俯仰角期望值θe设为

(20)

h0为根据机器人尺寸设定的阈值。

为保证控制平滑性,竖直方向质心位置和机身俯仰角轨迹基于三次多项式,即

x(t)=at3+bt2+ct+d

(21)

x为机身竖直方向位置或俯仰角,约束条件为

x(t0)=cz,0,x(tf)=cz,f

x(t)=x0+(xf-x0)(3-2t)t2

(22)

(23)

机身其余状态的期望值设为定值。

3 运动控制

3.1 摆动腿控制

摆动腿通过带前馈的PD算法控制,前馈项为

(24)

(25)

τs为各关节的期望力矩;Kp,fb和Kd,fb为增益矩阵。

3.2 机身控制

机身状态采用模型预测控制[17]。机身状态为

(26)

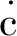
在坡度小于15°区域内，农村居民点斑块面积与数量占比高达91.9%与86.8%。在小于5°区域农村居民点密度、平均面积与标准差高出其他区域较多，而5°～15°区域内斑块数量与景观形状指数大于0°～5°区域，体现出0°～5°区域内农村居民点具有连片聚集大规模的特征，而5°～15°区域内农村居民点斑块更加碎小、并具有离散分布特性。随着坡度增大农村居民点总面积、面积比例、数量等各项指数均减小，且在坡度大于25°时降至极低水平，表明坡度对农村居民点分布与规模均具有极大的影响。农村居民点形状指数在0°～5°区域内最高，表明区域内农村居民点形状复杂，而其他区域差异不明显。

(27)

(28)

(29)

fi∈R3为支撑腿i受到的地面反作用力;ri∈R3为从机身质心到fi作用点的距离;m为机器人的质量;g∈R3为重力加速度;I∈R3为机器人的惯性张量;R为从机身坐标变换到世界坐标的旋转矩阵。定义[x]×∈R3×3为关于x的斜对称矩阵,使得对于所有的x、y∈R3,有[x]×y=x×y∈R3。

对于爬阶梯运动,横滚角可视为0,但机身俯仰角为0的假设不成立。为此,相较文献[16],本文在机器人动力学中考虑了机身俯仰角,有

(30)

对于角速度较小的运动,有

(31)

该模型的求解可转化为以下模型预测控制问题,即:

(32)

xt+1=Atxt+Btutt=0,…,n-1

(33)

ut,min≤Ctut≤ut,maxt=0,…,n-1

(34)

Dtut=0t=0,…,n-1

(35)

xt为时刻t的机身状态;ut为时刻t的控制输入(支撑腿足端接触反力Ft,r);n为预测的步数;Qt和Rt为权重的对角半正定矩阵;At和Bt为离散时间系统动力学;ut,min、Ct和ut,max为摩擦锥约束;Dt为1个支撑腿选择矩阵。力Ft,r经坐标变换和腿部雅可比计算得到支撑腿各关节期望扭矩τe,i。

3.3 整机控制框架

控制器系统框架如图4所示。

图4 机器人“盲爬”阶梯控制器系统

反馈数据模块处理各传感器的反馈数据。状态估计模块根据状态估计算法估计机身状态信息。机身规划模块规划机身状态的参考轨迹,输入模型预测控制模块进行计算。腿部控制器接收相应腿足端的期望位置、速度和前馈力,经逆运动学解算及PD控制算法计算各腿关节期望力矩τi,最终发送给关节驱动器。

4 仿真及实验验证

4.1 实验系统搭建

实验对象为宇树科技的A1机器人,样机和模型如图5所示。机器人每条腿有3个由电机驱动的关节(侧摆、髋、膝),每个足端有1个气囊,可通过检测气压的变化检测足地接触事件。机器人部分参数如表1所示。

表1 A1机器人基本参数

图5 A1机器人模型

如图6a所示,机身质心理想高度hc为0.300 m,阴影部分为足端有效工作空间。“盲爬”时摆动腿最大期望摆动高度z0须大于阶梯台阶高度。实验机器人髋关节结构半径rh为0.040 m,足直径df为0.040 m,基于关节尺寸及关节限位,腿部实际全长为0.360 m,如图6b所示。经实际测试,最大安全抬脚高度为0.160 m。

图6 A1机器人足端运动范围

物理实验平台的硬件结构如图7所示。虚线框中为机器人内部硬件,其中,以太网交换机用于机器人与外部PC交互数据,底层控制器用于收集IMU反馈数据以及与关节电机驱动器通信。控制算法代码运行于处理器型号为Intel酷睿i7-9750H的笔记本电脑(PC)上的Linux系统。各数据通过Ethernet(UDP)以1 kHz的通信频率在PC和机器人之间传输。

图7 实验平台硬件结构组成及关系

4.2 仿真实验

仿真实验平台为Webots仿真软件。对如表2所示的规则阶梯Ⅰ和不规则阶梯Ⅱ进行了攀爬实验。不规则阶梯Ⅱ各级台阶尺寸如表3所示。仿真结果数据从机器人在平坦地面加速完成后开始记录。

表2 仿真实验的阶梯信息

表3 阶梯Ⅱ尺寸信息

爬阶梯Ⅰ仿真实验结果如图8所示。阶梯Ⅰ整体“坡度”近似为24°。机器人分别在第0.767 s(A点)开始踩上第1级台阶水平面,在第4.748 s(B点)爬上整个阶梯。攀爬过程中机器人实时估计的阶梯“局部坡度”与阶梯整体“坡度”一致,且机身俯仰角能跟随估计“坡度”调整变化以适应阶梯地形。攀爬速度设定值为0.55 m/s。实际平均速度为0.53 m/s。

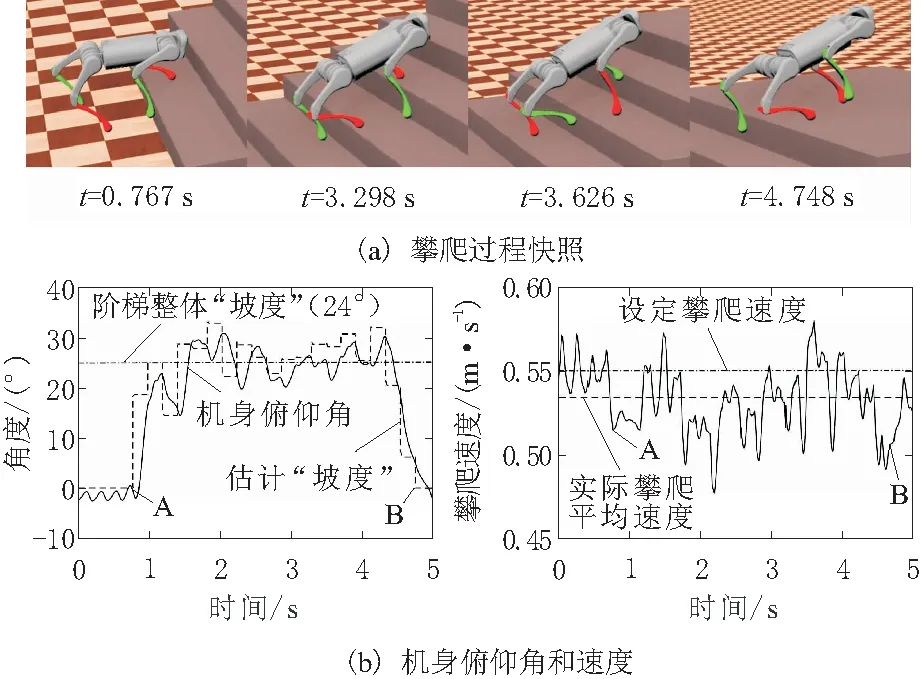
图8 爬阶梯Ⅰ仿真实验结果

爬阶梯Ⅱ仿真实验结果如图9所示。机器人分别在第0.667 s(C点)开始踩上第1级台阶水平面,在第4.439 s(D点)爬上整个阶梯。由于阶梯Ⅱ各级台阶尺寸不规则,表现为攀爬过程中实时估计的阶梯“局部坡度”在较大范围内变化。攀爬过程中速度设定值为0.52 m/s,实际平均速度值为0.50 m/s。

图9 爬阶梯Ⅱ仿真实验结果

爬阶梯Ⅰ实验中,在t=3.298 s机器人右前摆动腿抬起时与阶梯台阶竖直面发生磕碰,如图8a所示。检测到该事件后,“盲爬”运动规划器将右前腿足端世界坐标系x向的期望位置被设为当前实际位置,当足摆动到期望的最高位置后,x向继续按原规划摆动,足端最终落在上一级台阶水平面上,运动过程细节快照如图10a所示。在t=3.626 s机器人左前摆动腿落下时与阶梯台阶竖直面发生磕碰,如图8a所示。检测到该事件后,将足端在世界坐标系x向的期望位置设为当前位置往后1 cm,直到完全落下,转为支撑相。运动过程细节快照如图10b所示。在爬阶梯Ⅱ仿真实验中也出现了类似的情况,结果如同前一实验情形。

图10 爬阶梯Ⅰ摆动腿发生磕碰后运动快照

4.3 物理平台实验

实验基于表4和图11所示的阶梯Ⅲ和Ⅳ,其台阶高度分别达到了机器人腿部全长的29.17%和30.56%。

表4 物理平台实验的阶梯信息

图11 实验阶梯

实验结果如图12和图13所示,图中线缆为用于机器人和PC通信的网线。机器人分别在第1.100 s(E点)和1.000 s(I点)进入2个阶梯地形,第9.000 s(H点)和4.400 s(J点)爬上阶梯顶平面。机器人前脚刚踏上阶梯第1个台阶时,机身俯仰角立刻根据估计出的局部“坡度”进行调整,而后续攀爬过程中机身俯仰角跟随估计的“虚拟坡度”角度变化以适应阶梯地形。机器人爬阶梯Ⅲ和Ⅳ的平均速度分别为0.50 m/s和0.60 m/s,相应的无量纲速度Fr达0.27和0.32。

图12 爬阶梯Ⅲ实验结果

图13 爬阶梯Ⅳ实验结果

对于阶梯Ⅲ,由于台阶深度较大,机器人在攀爬过程中存在4只脚都在同一个台阶水平面上的情况,如图12a中图片2所示。该时刻处于图12b中F(左前与右后腿刚切换为支撑腿)和G(左前与右后腿支撑相结束)点之间,此时“局部坡度”为0,机身俯仰角也为0。当遇到台阶时估计“坡度”和机身俯仰角会随阶梯台阶“坡度”相应变化,最终表现为角度数据呈现周期性。对于阶梯Ⅳ,攀爬过程中估计的阶梯“坡度”和机身俯仰角能基本维持在阶梯整体“坡度”值附近,如图13b所示。

5 结束语

本文四足机器人快速“盲爬”阶梯策略通过估计阶梯局部信息,保证运动规划的合理性,对摆动腿与阶梯台阶的磕碰事件进行了实时检测及处理,对摆动腿和机身的运动进行了规划,使用模型预测算法对机身状态进行了控制。四足机器人可“盲爬”台阶高度相对腿较长的阶梯,且攀爬速度较快。