基于3-5-3多项式插补的六轴机器人轨迹优化

冯建超,鲁文其,林军华,鲁玉军,岑国建

(1.浙江理工大学机械工程学院,浙江 杭州 310018;2.迈得医疗工业设备股份有限公司,浙江 台州 317607;3.宁波中大力德智能传动股份有限公司,浙江 宁波 315301)

0 引言

多轴机器人在生产生活中扮演着重要角色[1-5],已被广泛应用于工业生产、医疗设备和国防军事等社会领域[6-8]。在多轴机器人的轨迹规划研究中,轨迹规划的优劣对于机器人作业完成的质量有着重要影响[9-10]。目前已经研究出众多的轨迹规划方法[11-14],并且在轨迹规划中会根据很多优化指标来进行轨迹优化[15-19]。如文献[20]采用了3次多项式插值法进行轨迹优化,该方法通过引入2个虚拟插值点,从而达到运行过程中速度和加速度稳定的目的,但是存在因为3次多项式插值法无法做到使加速度和加加速度也保持平滑和连续,所以机器人在实际运行中会产生抖动的问题。文献[21]和文献[22]提出了一种高阶非均匀有理B样条插补的控制方法,能够使多轴机器人工作时轨迹转弯处不平滑,从而容易产生变速冲击的问题得到有效改善,但是存在计算相对比较复杂的问题。

在使用3次多项式插补法时能够保证位移和速度保持连续,而加速度轨迹无法保持连续,且位移和加速度轨迹的各关节末端点均不为0,加速度轨迹在起始点存在跳变,容易造成启停抖动;在使用5次多项式插补法时能够保证位移、速度和加速度都保持连续,且加速度轨迹的起始点和末端点均为0,可以避免启停抖动的影响,但是相对于3次多项式而言,整个轨迹规划过程都采用高阶多项式的计算量会过于复杂。对此,为了给六轴机器人提供一种能优化加速度连续性、启停稳定性又能简化计算量的控制策略,提出了一种基于3-5-3多项式插补的机器人轨迹规划控制策略,该方法通过设置2个插值点,利用5次多项式对3次多项式进行插补轨迹优化,下面对其原理进行阐述及验证。

1 5次多项式插补轨迹规划

5次多项式有6个需要求解的多项式系数,可以同时设置起始点和目标点的约束条件,包括角度、角速度和角加速度,设关节角满足以下公式,即

(1)

用θ0和θf表示2个相近的轨迹点,可以将其看成一段轨迹的起始点和终止点,并用v0和vf表示起始速度和终止速度,所以可以得到表达式为

(2)

将约束条件代入式(1),可以求得所需的多项式系数,从而得到5次多项式轨迹规划的轨迹,即

(3)

2 基于3-5-3多项式插补的机器人轨迹规划控制

5次多项式插补法轨迹规划可以保证位移、速度和加速度都保持连续,而3次多项式插补法轨迹规划仅能保证位移和速度保持连续,无法保证加速度保持连续,且3次多项式轨迹规划的各关节加速度轨迹在起始点存在跳变,在末端点均不为0,容易造成启停抖动,影响机器人关节运行的稳定性。

为了解决上述问题,提出了一种基于3-5-3多项式插补轨迹优化的控制方法,在3次多项式插补法轨迹规划的基础上,通过设置插值点,在插值点之间插补5次多项式轨迹,充分利用5次多项式能够保证加速度保持连续的优点,下面对其原理进行阐述。

首先,使用3次多项式对机器人轨迹的起始点和终止点之间进行插补,将关节角和时间记作函数θ(t),让函数依次通过每个路径点,3次多项式的表达式为

θ(t)=a0+a1t+a2t2+a3t3

(4)

由于初始点和终止点的速度都是0,其中tf表示为结束时间,则得到

(5)

运动轨迹上的关节速度和加速度为

(6)

将初始点和终止点的速度和加速度代入到式(4)和式(6)可以得到

(7)

根据以上条件,求解可以得到以下系数代入到式(4),即

(8)

在路径上设置插值点,将路径点上2个相邻的插值点作为该段插值路径的初始点和终止点,此时关节速度肯定不为0,所以需要计算过路径点的3次多项式插值表达式,此时的速度约束条件为

(9)

将约束条件代入式(4)和式(6)可得

(10)

根据以上条件,求解可以得到以下系数代入式(4),即

(11)

其次,为了保证加速度轨迹保持连续以及避免3次多项式启停时会产生冲击的问题,对3-5-3多项式的样条插值函数进行构造。

在插值点处,样条曲线是一个k次多项式,它具有保持k-1阶导数连续性的优点。3-5-3多项式的样条插值函数具有以下特征:1阶导数表示速度轨迹的连续性;2阶导数表示加速度轨迹的连续性;3阶导数表示轨迹的稳定性。

3-5-3样条多项式的通式为

(12)

未知系数aj1i、aj2i、aj3i为第j个关节轨迹中3段样条插值函数的第i个系数;j=1,2,…,n,n为关节个数;hj1(t)、hj2(t)、hj3(t)分别为第j段关节中的3段轨迹,3段轨迹依次是3次多项式轨迹、5次多项式轨迹和3次多项式轨迹。

用Xji表示第j段关节的插值位置,其中i=0,1,2,3,表示4个插值点的序号,包括起始点、终止点和2个插值点。在笛卡尔坐标系中Xji表示机器人空间坐标通过逆运动学计算得到的关节角。

轨迹规划有以下已知条件:初始点和末端点的速度和加速度(速度一般取0),第j个关节中每一段轨迹的初始点Xj0、插值点Xj1和Xj2、末端点Xj3,并保证插值点间的速度和加速度保持连续。从而推导计算得到系数aji和插值点的关系式为:

A=

(13)

t1、t2、t3为第j段关节的3段多项式插值的时间。式(13)为3-5-3多项式系数a的计算公式。

根据式(13)可得到式(12)的多项式系数,即可得到优化后的3-5-3多项式插补轨迹规划方程。

3 实验测试与分析

3.1 实验平台设计

为了验证本文所提算法的有效性,设计了实验平台(如图1所示)进行测试,其主要由上位机、多轴运动控制器、伺服驱动器和六轴机械臂等组成。

图1 实验测试平台

3.2 六轴机器人性能测试

为了验证本文算法有效性,对引入3-5-3多项式插补函数的六轴机械臂进行性能测试。

关节1的位置、速度和加速度实验波形如图2所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节1运行启停抖动,使位移轨迹产生偏移;引入算法后,关节1轨迹在约t=1.7 s和t=3.2 s时引入插值点,位移轨迹从0变化到1.6 rad,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点1.6 rad/s,在t=2.6 s时达到最低点 -0.7 rad/s,加速度轨迹在t=2.1 s时达到最低点-3.5 rad/s2,在t=3 s时达到最高点2.5 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

图2 关节1位置、速度和加速度波形

关节2的位置、速度和加速度实验波形如图3所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节2运行启停抖动,使位移轨迹产生偏移;引入算法后,关节2轨迹在约t=1.7 s和t=3.2 s时引入插值点,位移轨迹在-0.6 ～1.5 rad之间变化,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点1.6 rad/s,在t=2.6 s时达到最低点 -2.6 rad/s,加速度轨迹在t=2.1 s时达到最低点-6.2 rad/s2,在t=3 s时达到最高点5.5 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

关节3的位置、速度和加速度实验波形如图4所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节3运行启停抖动,使位移轨迹产生偏移;引入算法后,关节3轨迹在约t=1.7 s和t=3.2 s时引入插值点,位移轨迹在 -1.4 ～0.6 rad之间变化,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点1.4 rad/s,在t=2.6 s时达到最低点 -2.3 rad/s,加速度轨迹在t=2.1 s时达到最低点-6.0 rad/s2,在t=3 s时达到最高点5.0 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

图4 关节3位置、速度和加速度波形

关节4的位置、速度和加速度实验波形如图5所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节4运行启停抖动,使位移轨迹产生偏移; 引入算法后,关节4轨迹在约t=1.7 s和

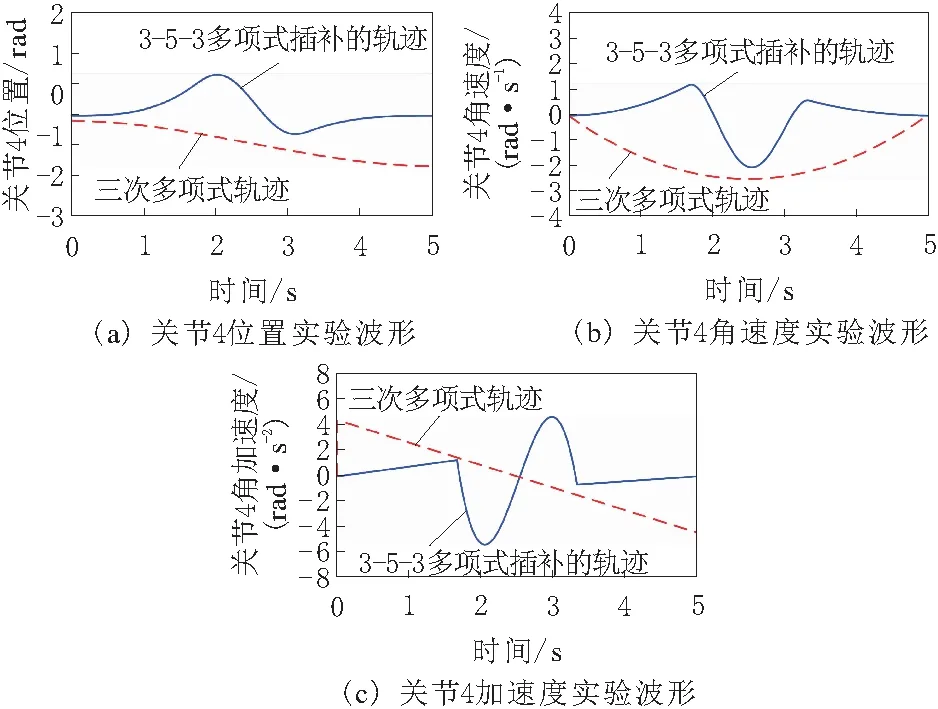
图5 关节4位置、速度和加速度波形

t=3.2 s时引入插值点,位移轨迹在 -1 ～0.6 rad之间变化,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点1.2 rad/s,在t=2.6 s时达到最低点 -2 rad/s,加速度轨迹在t=2.1 s时达到最低点-5.2 rad/s2,在t=3 s时达到最高点4.5 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

关节5的位置、速度和加速度实验波形如图6所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节5运行启停抖动,使位移轨迹产生偏移;引入算法后,关节5轨迹在约t=1.7 s和t=3.2 s时引入插值点,位移轨迹从 0.4 rad变化到1.9 rad,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点1.1 rad/s,在t=2.6 s时达到最低点 -0.5 rad/s,加速度轨迹在t=2.1 s时达到最低点-2.3 rad/s2,在t=3 s时达到最高点1.9 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

图6 关节5位置、速度和加速度波形

关节6的位置、速度和加速度实验波形如图7所示。由波形可知,引入算法前,仅能保证速度轨迹的始末点为0,加速度轨迹的起始点存在跳变,末端点不为0,造成关节6运行启停抖动,使位移轨迹产生偏移;引入算法后,关节6轨迹在约t=1.7 s和t=3.2 s时引入插值点,位移轨迹从0变化到1.3 rad,速度轨迹由于插入五次多项式轨迹在插值点之间会产生波动,在t=1.8 s时达到最高点0.7 rad/s,在t=2.6 s时达到最低点0.1 rad/s,加速度轨迹在t=2.1 s时达到最低点-1.8 rad/s2,在t=3 s时达到最高点1.5 rad/s2,加速度轨迹的起始点和末端点均为0,能够避免启停抖动影响关节启停的稳定性。

4 结束语

为了解决3次多项式轨迹规划仅能保证位移和速度保持连续,无法保证加速度保持连续,且3次多项式轨迹规划的加速度轨迹在起始点存在跳变,在末端点均不为0,容易造成关节电机启停抖动,使位移轨迹产生偏移的问题,提出了一种基于3-5-3多项式插补轨迹规划控制方法,在3次多项式轨迹规划的基础上,通过插入2个插值点时间t,将路径划分为3段,根据设置的插值点时间t计算得到插值函数的系数a,从而得到3-5-3多项式插值函数的表达式。

由实验测试结果可知,引入3-5-3多项式插值函数后,在插值点之间插入5次多项式轨迹规划的轨迹,使得各关节加速度轨迹在起始点和末端点均为0,可以避免启停时产生抖动的问题,保证机器人启停时的稳定性,且各关节的加速度运算关系能够实现连续,但是相对的,轨迹插值点之间会产生5次多项式的波动影响,这就需要后续研究更高阶的混合多项式插补等方法使轨迹运行更加平滑稳定。