泡沫铝夹芯板厚度对防爆墙侵彻深度影响研究*
陈海洋,金翰呈,李雄姿,岳宝兵,李小双,肖定军,
(1.西南科技大学 环境与资源学院,四川 绵阳 621010;2.绵阳市海川爆破工程有限公司,四川 绵阳621010)
0 引言
防爆墙作为一种新兴的防护材料,引起了学者的广泛关注。近年来,国内外许多学者通过实验研究、数值模拟及理论分析的方法对防爆墙的抗冲击性能[1-4]和抗侵彻性能[5-7]进行了研究,尤其是对于引起防爆墙结构破坏的相关因素,如爆炸冲击波、破片等进行了深入研究,探索了爆炸冲击波冲击防爆墙的绕射规律、消波规律及机理;但对影响防爆墙本身结构稳定的因素,如填充介质等方面的研究还不足,大部分研究工作还集中在砂土介质、混凝土介质等方面[8-10]。
由于防爆墙起防护作用的主要是其填充介质,且复合结构的填充介质具有单一介质(一般为砂土)所不具备的优势,如具有很强的过载承受能力、优异的材料性能及力学性能、良好的散热性能以及相对较小的质量(低密度)等优点[11],同时,考虑到填充介质的成本及地质条件限制,不可能通过无限制增加其厚度来提高防护性能,因此开展复合结构填充介质厚度对防爆墙侵彻深度影响研究可为防爆墙的防护分析和厚度优化提供理论参考。目前对于复合结构的研究主要集中在其本身的性能方面,而对其在防爆墙方面的应用尚未见报道。在材料结构组合方面,相关学者通过数值模拟研究发现,随着材料的应变率影响因子/黏度系数的增大或材料屈服强度的减小,材料中的强应力波衰减速率增大[12];而且,材料声阻抗值越大,应力峰值衰减就越慢[13]。因此,屈服强度相对较低、应变率较敏感、波阻抗较低的材料理论上成为了防护结构的首选材料。在材料类型选择方面,多孔脆性材料(如多孔岩石或多孔混凝土)和泡沫材料在防护工程领域中的应用近年来得到了较多关注。相关研究表明,在多孔材料(多孔岩石[14]、硬质聚氨酯泡沫[15-16]、泡沫铝[17]等)中,塑性压缩过程是多孔材料塑性力学行为的主要特征,孔隙坍塌效应使得应力波的衰减加快,从而起到很好的抗震吸能作用。然而,多孔岩石和多孔混凝土虽然能够很好地起到削波吸能作用,但是其抗压强度不能满足要求。
考虑到夹芯结构的优点,本文拟开展泡沫铝夹芯板厚度对防爆墙防护性能的影响研究。通过物理实验和理论分析确定数值模拟模型的材料结构、材料模型、材料密度,然后在此基础上通过数值模拟分析填充介质厚度与破片侵彻深度之间的变化规律以及填充介质对破片的能量耗散情况,为合理设计防爆墙结构以及有效提高其对破片的防护能力提供参考。
1 数值模拟
1.1 模型建立
对破片侵彻问题的研究主要采用现场实验、数值模拟等方式,但现场实验成本高、危险性大。为此本文采用数值模拟的方式进行相关研究,AUTODYN显示动力分析软件被广泛应用于爆炸与高速侵彻过程的模拟,其有效性已得到验证。为此,本文利用AUTODYN显示动力分析软件对不同初始速度破片侵彻加入了泡沫铝夹芯板填充介质防爆墙的过程进行有限元模拟分析。因为防爆墙的抗侵彻能力主要体现在填充介质的性能上,因此将防爆墙简化为填充介质模型。由于简化后的模型为对称模型,为提高计算效率,建立1/4三维数值模型,破片尺寸为80 mm×40 mm (为减小破片长径比对计算结果的影响,破片模型采用的长径比为2∶1),防爆墙模型尺寸为1 000 mm×1 000 mm×1 000 mm,破片和防爆墙均采用拉格朗日算法,其模型示意图见图1。
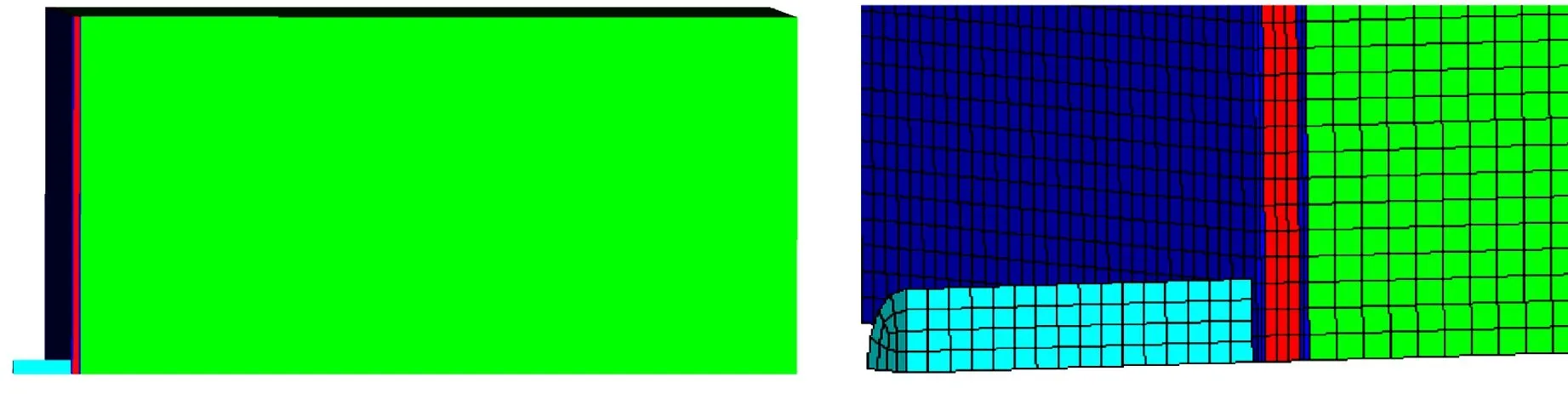
图1 模型示意图
1.2 材料模型及参数选择
1)砂土介质模型及参数选择
防爆墙的填充介质主要为砂土,采用*MAT_SOIL_AND_FOAM材料模型[18],此材料模型没有应变硬化,屈服极限仅与压力p有关:
(1)
式中,a0、a1、a2为塑性屈服常数,p为介质所受压力。
参数取值见表1。表1中:ρ为土体密度,g/cm3;G为剪切弹性模量,MPa;K为卸载时的体积模量,MPa;PC为拉应力系数;VCR为体积沙漏选项;REF为是否使用参考几何初始化压力选项。

表1 砂土材料参数
2)泡沫混凝土材料模型及参数选择
泡沫混凝土材料模型的参数采用文献[19]中相关参数(见表2)。
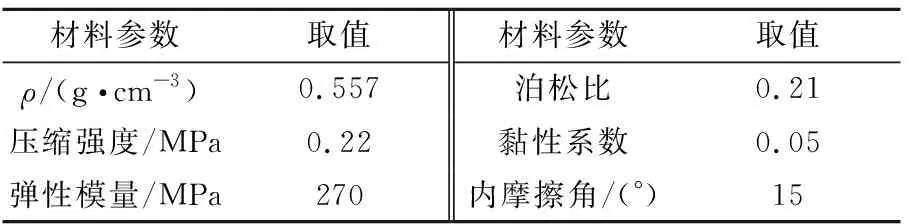
表2 泡沫混凝土材料参数
3)泡沫铝材料模型及参数选择
泡沫铝夹芯板材料包括面板和夹芯层,其中面板采用 LY-12铝合金,其材料参数为:密度2.78 g/cm3,弹性模量68 GPa,屈服强度310 MPa,泊松比0.33。
泡沫铝芯层材料采用Crushable_Foam本构模型,其参数根据Gibson提出的预测泡沫金属弹性模量和应力平台的平方函数模型[20]进行计算:
(2)
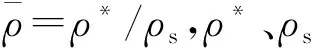
(3)
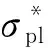
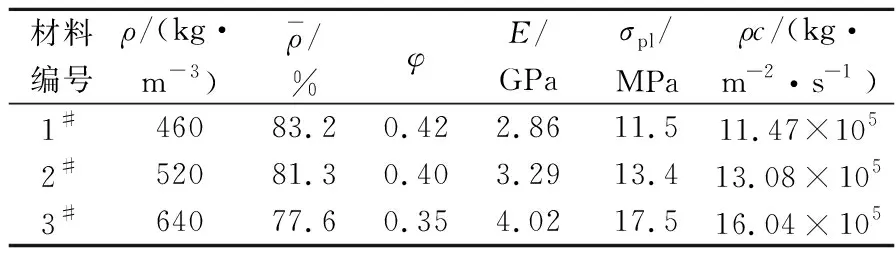
表3 泡沫铝材料参数
为了防止泡沫铝单元在计算过程中出现过度变形,导致其产生负体积而使计算终止,在此模型基础上添加泡沫铝材料失效准则:当主应变大于0.4时,将失效单元删除[23]。
4)破片材料模型
破片材料采用不锈钢,密度为7.86 g/cm3,弹性模量为190 GPa,屈服应力为689 MPa,强度模型采用Piecewise JC本构模型。
1.3 网格合理化分析
有限元模型网格的划分必须兼顾计算效率与计算精度[24]。网格尺寸与数量关系见图2。由图2可知,随着网格尺寸的变小,网格数量呈指数级增长,这虽然提高了计算精度,但是在计算精度提高不大的情况下却极大降低了计算效率。为了确定较为合理的网格尺寸,分别设计了4、5、6、10 mm的网格尺寸梯度,并计算了破片在523 m/s初始速度下的冲击过程(见图3)。综合分析各计算结果,本文最终选定的网格尺寸为6 mm。
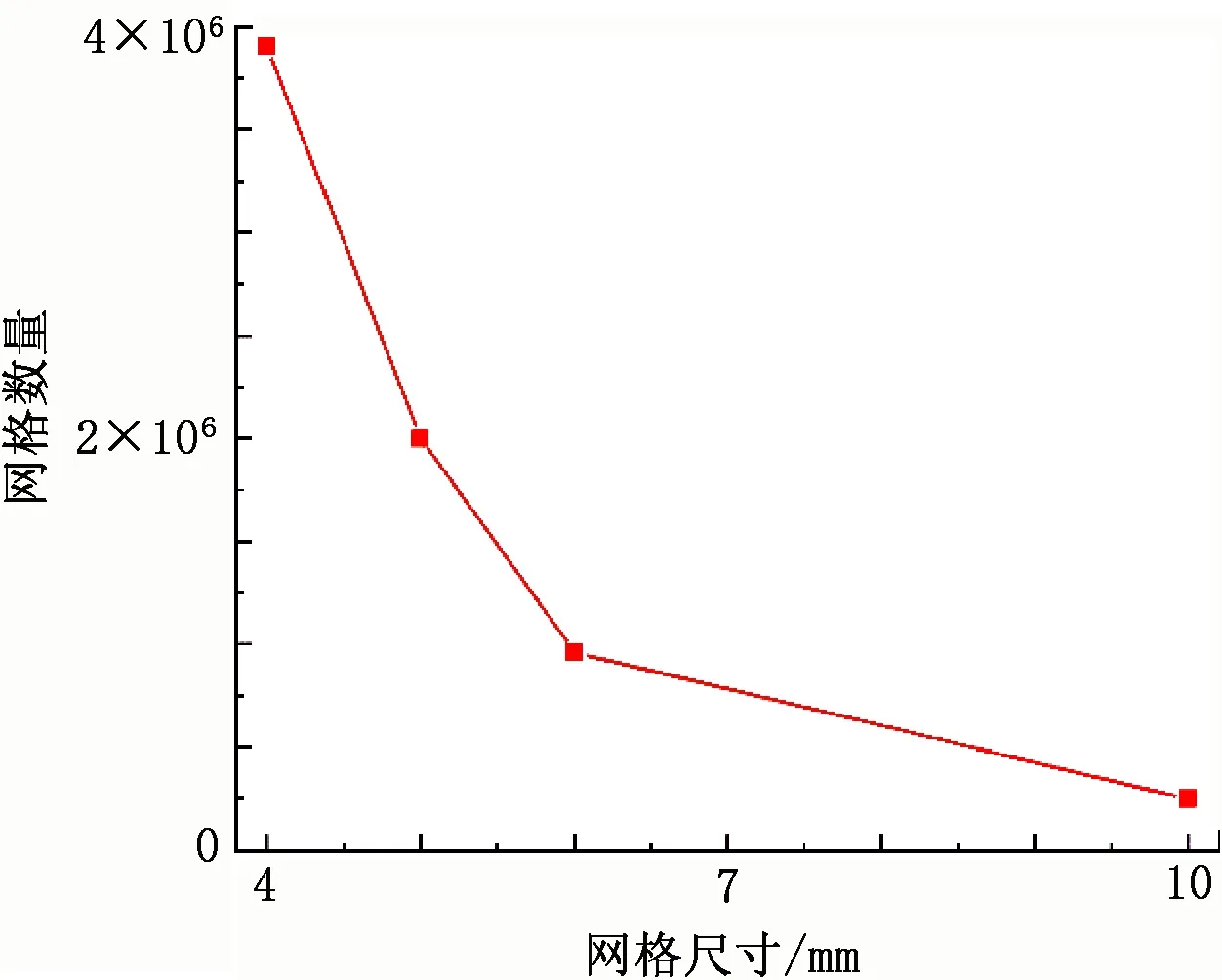
图2 网格尺寸与网格数量的关系
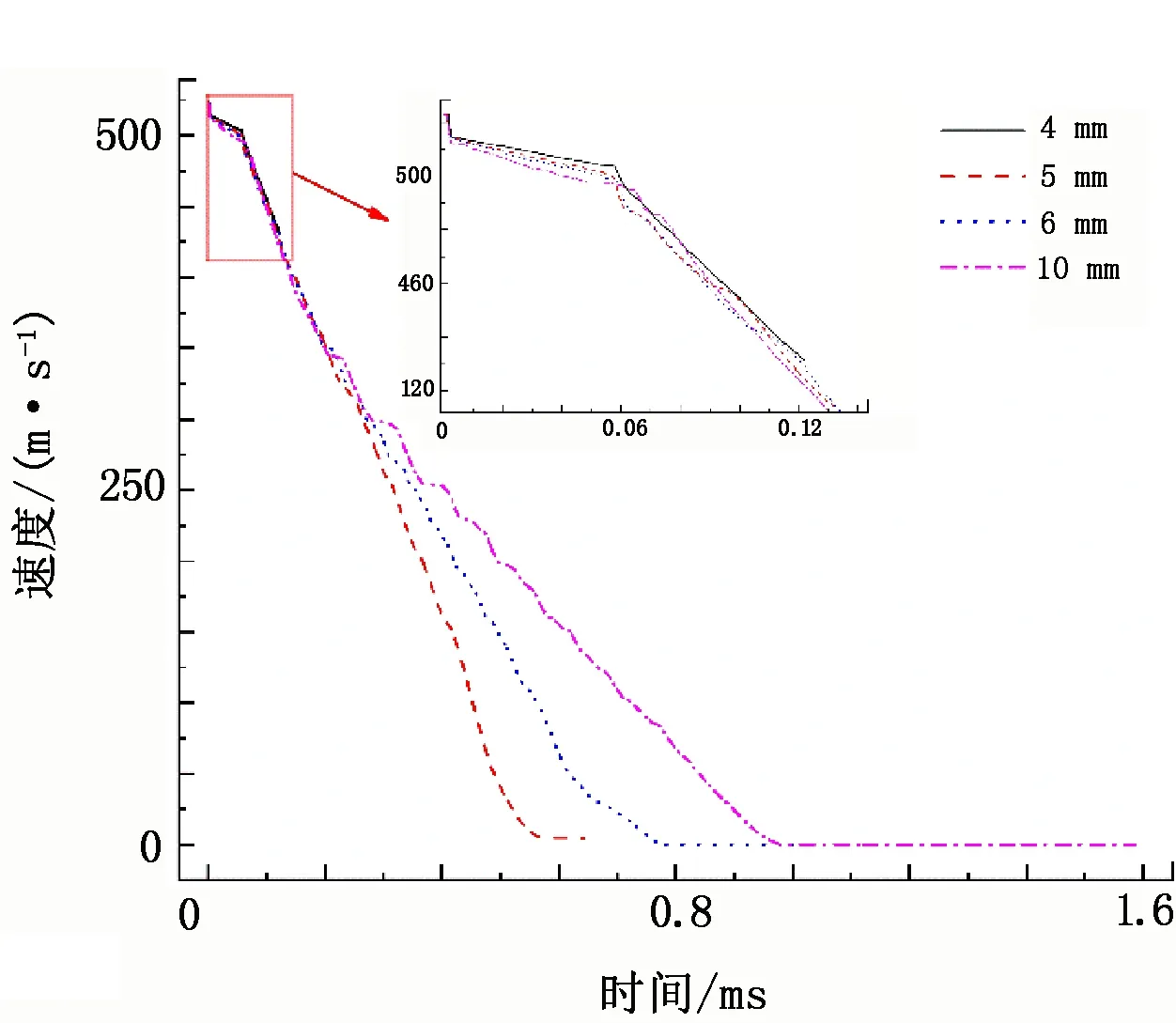
图3 网格尺寸与破片速度的衰减关系
1.4 模拟可靠性验证
为了验证数值模拟结果的可靠性以及材料本构模型和参数的合理性,采用一级轻气炮进行物理实验。
1)实验设备与材料
实验设备包括一级轻气炮、磁测速、应变片、DH5922N应变测试仪、砂箱等。
实验材料包括304不锈钢、砂土、泡沫混凝土、单层板结构泡沫铝及夹芯结构泡沫铝。
2)实验设计
由于防爆墙起主要防护作用的是填充介质,因此将砂箱作为填充介质的外部约束结构。破片尺寸为80 mm×40 mm,为减小尺寸效应及考虑成本,砂箱宽度和高度均设置为40倍弹体半径[10],长度为1 m。设备布置见图4。

图4 设备布置图
采用密度为1.8 g/cm3、含水率为2%的砂土作为主要的填充介质,并将泡沫混凝土、泡沫铝板等置于砂土介质前。为得到破片在填充介质中的速度衰减规律,将应变片分别贴在砂箱迎撞面处以及分别距迎撞面20、40、45、60 cm处。
为了确定较为合理的材料结构,分别设计了单层板结构泡沫铝(monolayer foamed Al)、夹芯结构泡沫铝(double-layer foamed Al)、单层板结构泡沫铝与泡沫混凝土复合结构(monolayer foamed Al/concrete foam/monolayer foamed Al)、夹芯结构泡沫铝与泡沫混凝土复合结构(double-layer foamed Al/concrete foam/double-layer foamed Al)等4种结构,得到其在不同初始速度破片冲击下的侵彻深度以及破片在填充介质中的速度衰减规律,并与数值模拟结果进行对比。
3)实验结果
(1)应变测试结果
应变测试结果见图5。由图5可知,每一组应变结果均小于200×10-6,在砂箱的弹性变形范围以内,可以保证每次测试时砂箱都在相同位置发生变形。
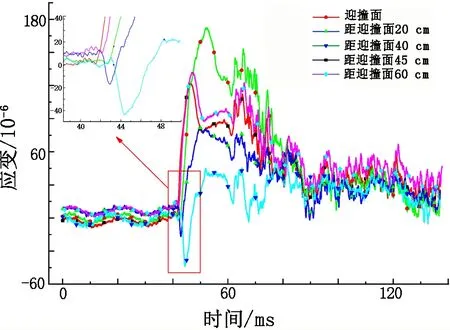
图5 应变测试结果
(2)速度衰减过程
通过计算应变值之间的时间差,可以得到破片在该段范围内的平均速度,将计算结果进行拟合,从而得到破片在填充介质中的速度衰减过程(见图6)。由图6可知,破片速度衰减趋势与数值模拟结果的吻合度较高。
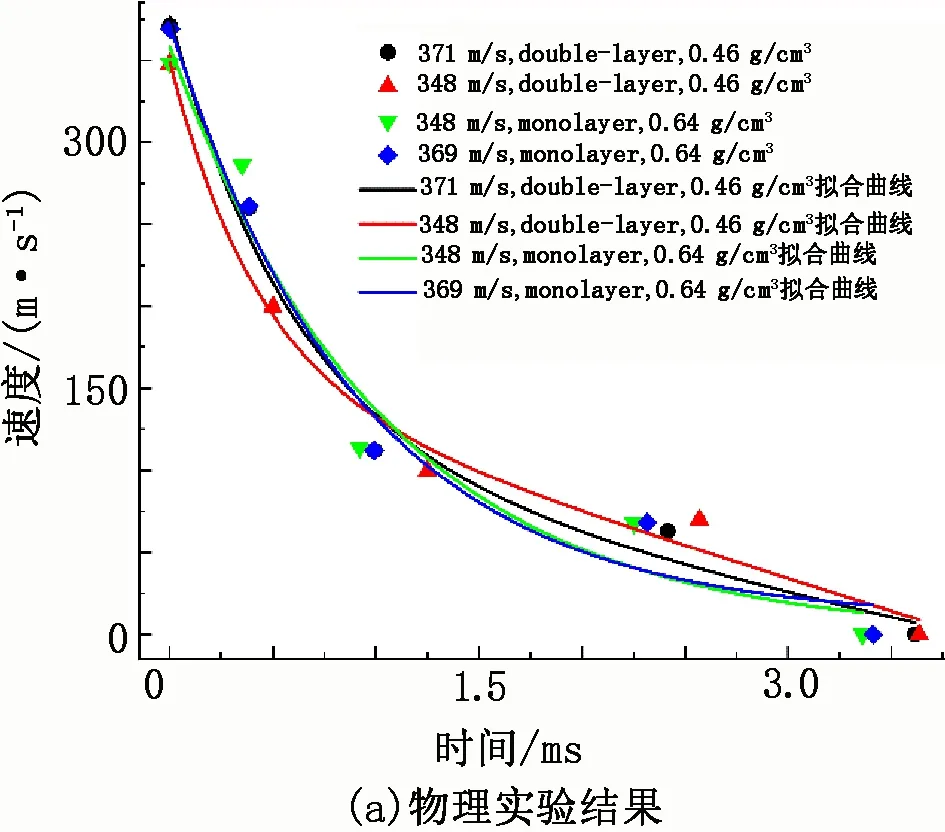
图6 破片速度衰减过程
(3)模拟与实验侵彻深度及误差对比
模拟与实验的侵彻深度(depth of penetration,DOP)及误差对比见表4。由表4可知,模拟与实验侵彻深度之间的误差均小于10%,表明数值模拟的结果较为可靠。
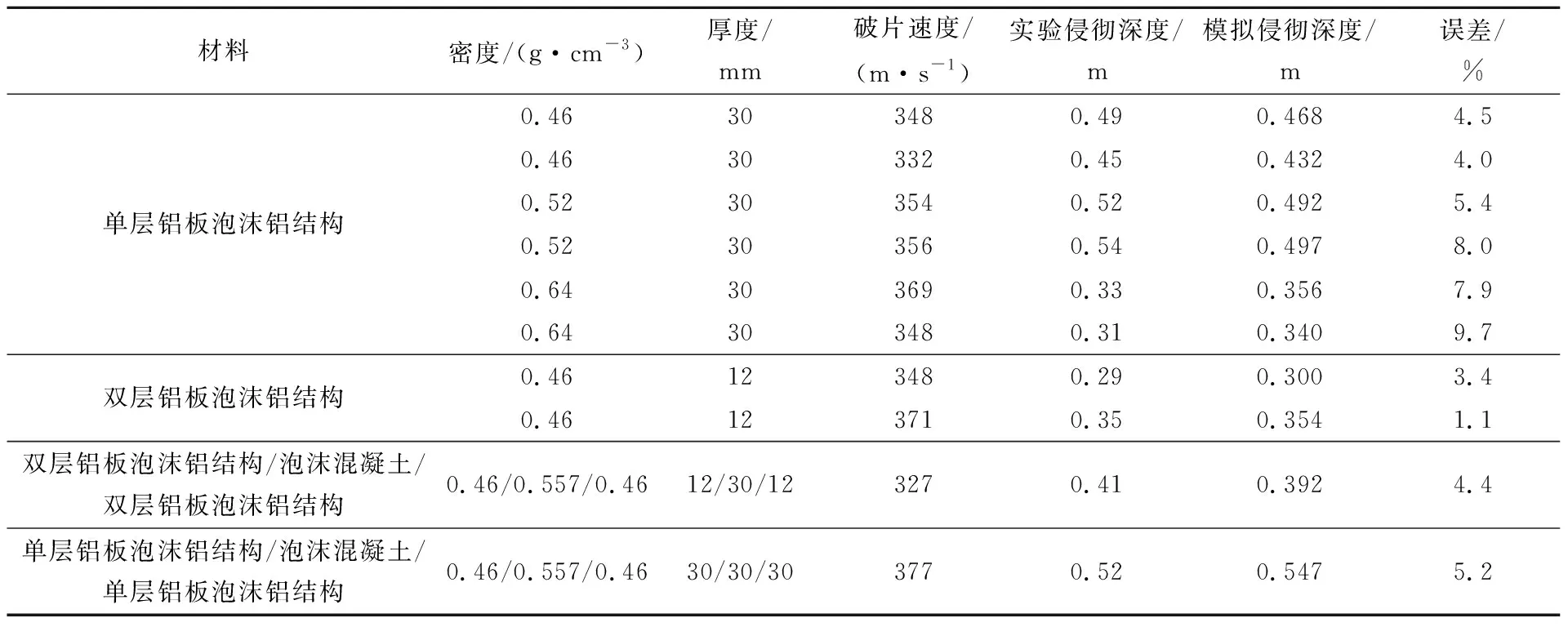
表4 模拟与实验侵彻深度及误差对比
(4)泡沫铝板的破口形状对比
泡沫铝板被破片冲击后形成的破口见图7。由图7可知,模拟与实验形成的破口形状大致相同。

图7 泡沫铝板的破口形状对比
综上可知,模拟与实验的结果吻合较好,表明数值模拟采用的本构模型、材料参数是比较合理的,能够较为可靠地对不同速度破片冲击防爆墙的过程进行仿真计算。
1.5 工况设计
通过分析实验结果,确定合理的材料结构,进行数值模拟工况设计。
1)材料厚度
由表4可知,在泡沫铝密度为0.46 g/cm3、速度为348 m/s时,材料厚度减少60%的情况下,破片侵彻深度反而下降了40.82%。这说明相较于单层泡沫铝结构,双层夹芯板结构能够在减小材料厚度的情况下提高防爆墙的防护能力。因此,数值模拟模型拟采用双层夹芯板结构泡沫铝。但是,综合考虑材料成本和防护能力,泡沫铝夹芯板应有一个最佳厚度。因此数值模拟中设计了不同厚度梯度的泡沫铝夹芯板结构。
2)材料波阻抗
有研究表明,加入波阻抗较低介质的多层结构对应力波强度的衰减和能量的吸收有着非常明显的作用[25-26];将“软”材料和“硬”材料交替层叠构成的多层结构对应力波的衰减和弥散有较强的作用[27-28]。有关现场实验表明[29]:防护层分层设置的结构对核爆炸冲击波峰值应力的衰减效果优于防护层单层设置的结构;且防护层分层设置的工程结构对核爆炸冲击波具有弥散效应,分层材料相同且各种材料的总厚度也相同时,采用周期循环布置时弥散效应明显加强,利用这一特性可显著降低核爆炸空气冲击波对脆性材料的破坏作用。
在碰撞或爆炸的冲击波峰值压力p≤100 MPa时,用弹性波理论分析物体在冲击载荷作用下所形成的应力波反射和透射问题,方法简单且非常有效[30]。
根据一维波动理论[31]可知,在一维线弹性情况下,假定强度为σi的入射波从声阻抗为ρ0c0的介质传播到声阻抗为ρ1c1的介质,令其波阻抗之比λ为
λ=ρ0c0/ρ1c1。
(4)
可知入射波经过交界面后透射波的强度σt和反射波强度σr为
σt=2σi/(1+λ),
(5)
σr=σi(1-λ)/(1+λ)。
(6)
由此可知,界面对应力波的反射和折射(透射)有较大影响,实验也证实了界面具有对冲击应变能的累积和阻滞作用[32],因此选择合适的分层结构能够起到较理想的削波作用。
各材料波阻抗计算式为
(7)
式中,Z为材料波阻抗,kg/(m2·s)。
泡沫混凝土的密度为557 kg/m3,弹性模量为270 MPa。泡沫铝夹芯板的面板采用 LY-12 铝合金,其材料密度为2 780 kg/m3,弹性模量为68 GPa,泊松比为0.33;泡沫铝芯层材料的参数见表3。由此,可得各材料的波阻抗:
=1.37×107(kg·m-2·s-1),
=11.47×105(kg·m-2·s-1),
=13.08×105(kg·m-2·s-1),
=16.04×105(kg·m-2·s-1)。
由计算结果可知:
Zplate Al>Zfoamed Al>Zconcrete foam。
可见防护材料中,泡沫铝夹芯板的面板波阻抗最大,泡沫铝芯层材料波阻抗次之,泡沫混凝土波阻抗最小。
在防护工程领域中,为了应对爆炸冲击下的高强度、高应变率载荷,防护材料一般采用“硬-软-硬”的夹层结构[33],因为不同波阻抗材料改变排列次序会影响结构的次生冲击波超压[34]。但是由表4可知,泡沫铝密度为0.46 g/cm3时,在泡沫铝夹芯板结构中间加入一层密度为0.557 g/cm3、厚度为30 mm的泡沫混凝土后,其侵彻深度在破片速度低于不加泡沫混凝土的情况下反而增大了,也就是说,加入泡沫混凝土后对夹芯层结构受到的应力波有增强作用(即增强了透射应力波的强度,使更多的应力波透射到了后面的结构层中),从而减弱了防爆墙的防护能力。因此,一味地添加波阻抗低的填充介质并不能提高防爆墙的抗侵彻能力,反而还有可能降低其防护能力。
综上,数值模拟中采用泡沫铝夹芯板结构。
3)材料密度
由表4可知,泡沫铝芯层密度为0.46 g/cm3时,在332 m/s速度破片冲击下,侵彻深度为0.45 m;在348 m/s速度破片冲击下,侵彻深度为0.49 m。泡沫铝芯层密度为0.52 g/cm3时,在354 m/s速度破片冲击下,侵彻深度为0.52 m;在356 m/s速度破片冲击下,侵彻深度为0.54 m。泡沫铝芯层密度为0.64 g/cm3时,在348 m/s速度破片冲击下,侵彻深度为0.31 m;在369 m/s速度破片冲击下,侵彻深度为0.33 m。综上可知,当泡沫铝芯层密度由0.46 g/cm3增加到0.52 g/cm3时,密度对侵彻深度的影响不太明显;而当泡沫铝芯层密度由0.52 g/cm3增加到0.64 g/cm3时,密度对侵彻深度的影响十分明显。
在相同密度下,0.46 g/cm3时的破片速度上升了4.82%,其侵彻深度增加了8.89%;0.52 g/cm3时的破片速度上升了0.56%,其侵彻深度增加了3.85%;0.64 g/cm3时的破片速度上升了6.03%,其侵彻深度增加了6.45%。由破片速度上升和侵彻深度变化趋势可知,密度为0.64 g/cm3时,破片速度上升对其侵彻深度的影响相对较小。因此,数值模拟采用密度为0.64 g/cm3的泡沫铝芯层材料。
综上,数值模拟采用密度为0.64 g/cm3的泡沫铝芯层,“硬-软-硬”夹芯结构。共设计35种工况,每种工况由泡沫铝板厚度和破片初始速度耦合而成。其中泡沫铝夹芯板的厚度t分别设计为0、12、24、36、48 mm,并将其放置在防爆墙的迎撞面;破片初始速度分别为200、500、800、1 200、1 500、1 800、2 100 m/s。研究泡沫铝夹芯板结构厚度变化对防爆墙防护性能的影响程度,以期为防爆墙的合理设计提供参考。
2 结果分析与讨论
2.1 破片速度衰减规律
破片速度衰减趋势见图8。
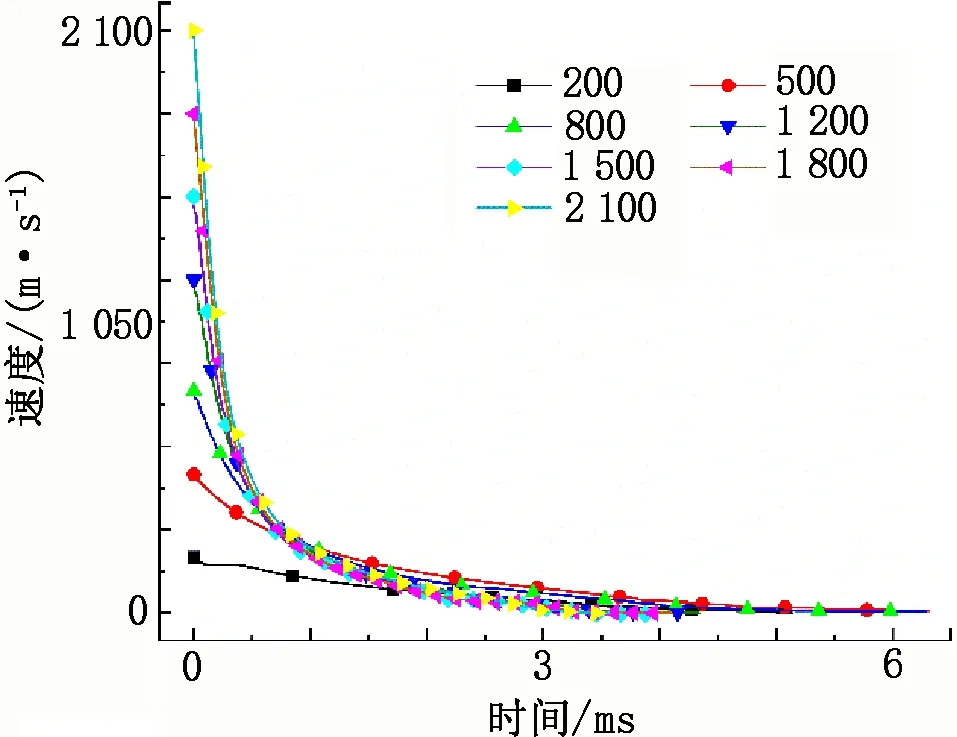
图8 破片速度衰减趋势
由图8可知:当砂土介质前面无泡沫铝夹芯板、破片速度为200 m/s时,破片运动时间约为5 ms;当破片速度为500 m/s和800 m/s时,破片运动时间约为6.3 ms;当破片速度为1 200、1 500、1 800 m/s时,破片运动时间约为4.2 ms;当破片速度为2 100 m/s时,破片运动时间约为3.6 ms。当泡沫铝夹芯板厚度为12 mm、破片速度为500 m/s和800 m/s时,破片运动时间大致相同,约为4.5 ms;破片速度为200 m/s和1 200 m/s时,破片运动时间均约为2.5 ms;破片速度为1 500、1 800、2 100 m/s时,破片运动时间大致相同,约为1.8 ms。当泡沫铝夹芯板厚度为24 mm、破片速度为500 m/s和800 m/s时,破片运动时间约为4.2 ms;当破片速度为200 m/s时,破片未穿透泡沫铝夹芯板,且速度衰减变缓,说明泡沫铝夹芯板在其屈服强度内能使破片速度衰减加快;当破片速度为1 200 m/s时,破片运动时间约为2.8 ms;当速度为1 500、1 800、2 100 m/s时,破片运动时间约为1.7 ms。当泡沫铝夹芯板厚度为36 mm、破片速度为500 m/s和800 m/s时,破片运动时间约为4.1 ms;当破片速度为200 m/s时,破片未穿透泡沫铝夹芯板,且破片运动时间较厚度为12 mm和24 mm时极大缩短,说明随着泡沫铝夹芯板厚度的增加,破片速度衰减加快;当破片速度为1 200 m/s时,破片运动时间约为3 ms;当破片速度为1 500、1 800、2 100 m/s时,破片运动时间依次减少,分别约为2.2、1.9、1.6 ms。当泡沫铝夹芯板厚度为48 mm、破片速度为500 m/s和800 m/s时,破片运动时间约为4.2 ms;当破片速度为200 m/s时,破片未穿透泡沫铝夹芯板;当破片速度为1 200、1 500、1 800、2 100 m/s时,破片运动时间分别约为2.6、2.2、1.8、1.5 ms。
2.2 泡沫铝夹芯板厚度对侵彻深度的影响
侵彻深度随破片初始速度的变化趋势见图9。
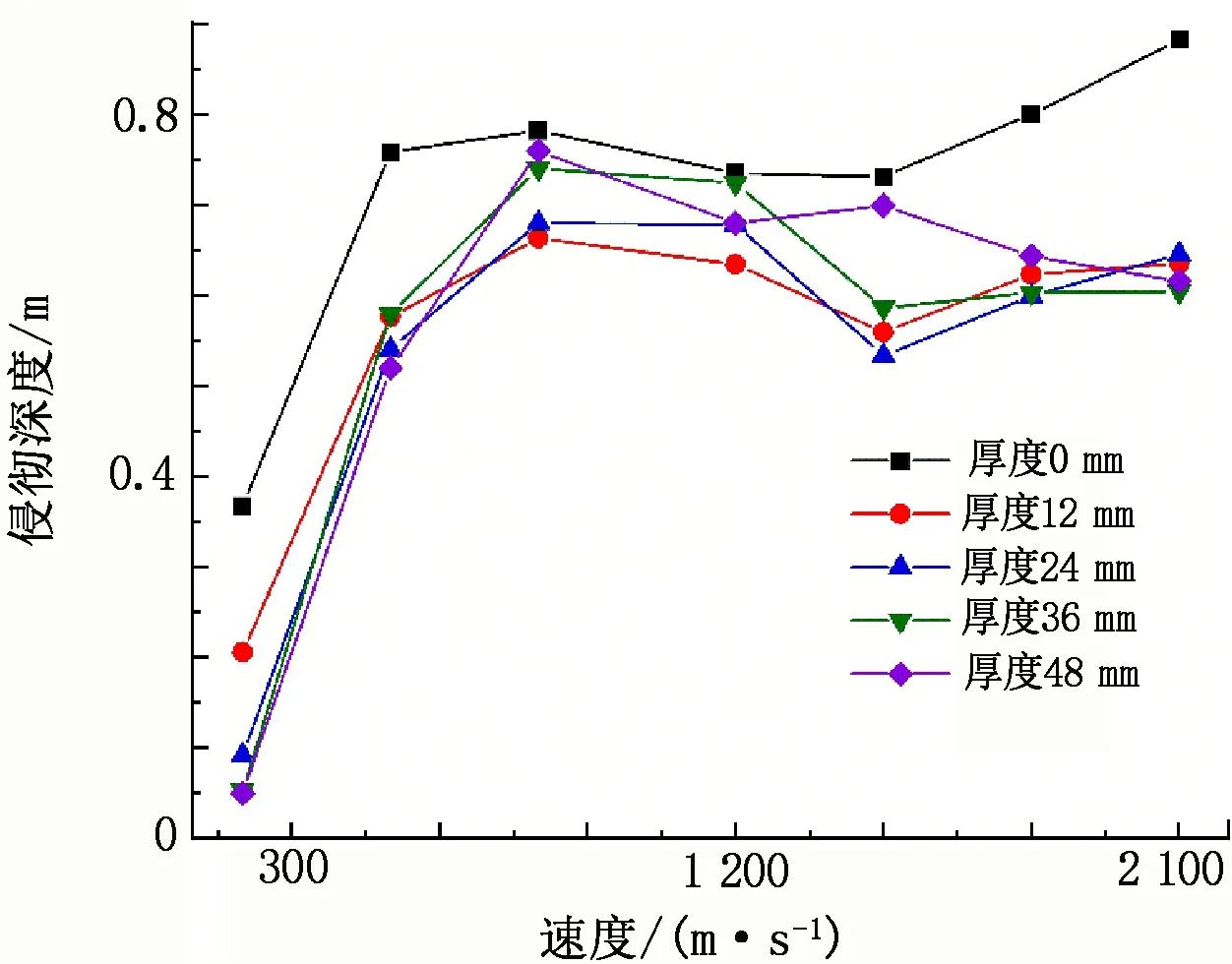
图9 侵彻深度随破片初始速度的变化趋势
由图9可知:当泡沫铝夹芯板厚度为0、12、24、36 mm时,在200~800 m/s速度内,破片侵彻深度随初始速度的增加呈上升趋势,此时破片侵彻深度主要由初始速度决定;当破片速度为800~1 500 m/s时,破片侵彻深度随初始速度的增大而减小,这可能是因为破片初始速度相对较大,破片在冲击过程中变形严重,导致破片侵彻深度减小;当破片速度为1 500~2 100 m/s时,破片侵彻深度随初始速度的增大而增大,此时破片变形达到一定程度后不再变化,主要由破片初始速度决定其侵彻深度,初始速度越大,破片侵彻深度越大。但当泡沫铝夹芯板的厚度为48 mm时,在200~1 500 m/s速度内,破片侵彻深度随初始速度的增大而增大,这说明在该速度范围内,破片变形程度相差不大,此时破片侵彻深度主要由初始速度决定;在1 500~2 100 m/s速度范围内,破片侵彻深度随初始速度的增大而减小。泡沫铝夹芯板厚度为48 mm时,其侵彻深度的临界速度较其他厚度泡沫铝板“滞后”,这可能是由于泡沫铝板厚度大,可视作单一介质,但穿透泡沫铝板进入砂土阶段后为复合介质,而泡沫铝夹芯板的波阻抗比砂土介质大,破片要达到相同的侵彻深度就需要更大的初始速度,从而导致其临界速度出现“滞后”现象。这一结果与文献[35-36]的研究结果一致。
破片侵彻深度随泡沫铝板厚度的变化趋势见图10。
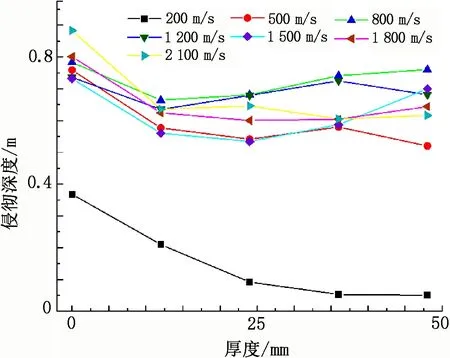
图10 侵彻深度随泡沫铝板厚度的变化趋势
由图10可知,破片速度为200 m/s时,随着泡沫铝夹芯板厚度的增加,其侵彻深度变小,且逐渐趋于稳定,这可能是因为后层的泡沫铝板发生变形消耗了破片冲击能量。加入泡沫铝夹芯板能够极大减小破片的侵彻深度,但是泡沫铝板的层数并不是越多越好。在相同速度破片冲击下,随着泡沫铝板层数的增加,破片侵彻深度反而还有可能增大,这说明在一定范围内,泡沫铝夹芯板厚度越大,其抗侵彻能力不一定越强。
每增加一层泡沫铝夹芯板对破片侵彻深度的衰减度见图11。
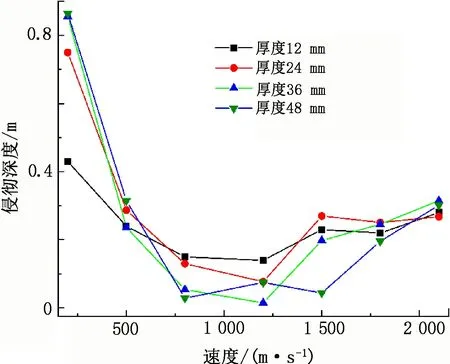
图11 填充不同厚度泡沫铝板时破片侵彻深度变化情况
由图11可知:当破片初始速度为200 m/s、泡沫铝夹芯板厚度为48 mm时,破片侵彻深度最小;当破片初始速度为500 m/s、泡沫铝板厚度为48 mm时,破片侵彻深度最小;但当泡沫铝板厚度为12 mm时,破片侵彻深度同比减幅最大。当破片初始速度为800 m/s和1 200 m/s时,12 mm厚度的泡沫铝板被破片侵彻深度最小;当破片初始速度为1 500 m/s和1 800 m/s时,24 mm厚度的泡沫铝板被破片侵彻深度最小;当破片初始速度为2 100 m/s时,36 mm厚度的泡沫铝板被破片侵彻的深度最小。
2.3 能量耗散分析
破片冲击防爆墙的过程中,介质吸收的能量主要分为两个部分:一是破片变形吸收的能量,二是介质破坏吸收的能量[37]。则有
ET=EF+EP,
(8)
式中,ET为破片冲击过程中的总动能,EF为破片变形吸收的能量;EP为介质发生破坏吸收的能量。
假设破片在冲击过程中没有质量损失,则破片冲击过程中消耗的总动能可用下式计算:
(9)
式中,vi为破片的初始速度,vr为破片的剩余速度。
破片变形吸收的能量可用下式计算:
(10)
在破片侵彻防爆墙的过程中,填充介质发生破坏吸收的能量很难被直观地量化,因此采用单位面积吸收的能量Ea来表示,则
Ea=Ep/[n(2ρ1t1+ρ2t2)+ρsxs],
(11)
式中,n为泡沫铝夹芯板的层数,ρ1、ρ2、ρs分别为泡沫铝夹芯板面板、泡沫铝夹芯板芯层以及砂土介质的密度,t1为泡沫铝夹芯板面板厚度,t2为泡沫铝夹芯板芯层厚度,xs为破片侵彻进入砂土介质的深度。
相较于用破片侵彻深度来评估泡沫铝夹芯板的抗侵彻能力,采用单位面积吸收的能量可以更加直观地评估泡沫铝夹芯板抵抗破片侵彻能力的最佳层数。以200、800、1 500 m/s速度破片为例,其填充不同厚度泡沫铝夹芯板单位面积吸收的能量见表5。由表5可知:单位面积吸收的能量与破片侵彻深度呈负相关,单位面积吸收能量最多的泡沫铝夹芯板其破片侵彻深度最小:破片初始速度为200 m/s、泡沫铝夹芯板厚度为48 mm时,侵彻深度最小;破片初始速度为800 m/s、泡沫铝夹芯板厚度为12 mm时,侵彻深度最小;破片初始速度为1 500 m/s、泡沫铝夹芯板厚度为24 mm时,侵彻深度最小。这与此前得到的结论一致,该结论可为泡沫铝夹芯板厚度设计提供理论依据。
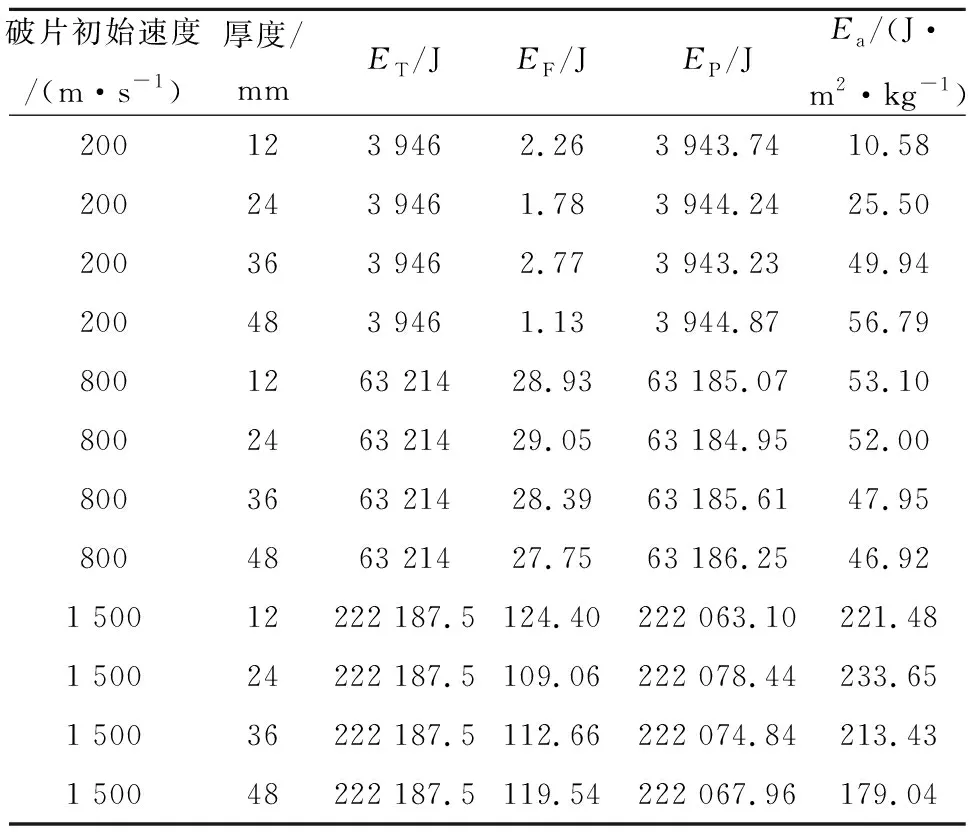
表5 单位面积吸收的能量
3 结论
本文采用物理实验、理论分析和数值模拟相结合的方法,分析了不同初始速度破片侵彻不同厚度泡沫铝夹芯板防爆墙的过程,得到了其速度衰减规律、侵彻深度规律以及能量耗散规律,形成以下主要结论:
a.破片侵彻深度随着初始速度的增大呈先增大后减小再增大的趋势,临界速度分别为800 m/s和1 500 m/s。
b.破片侵彻深度的临界速度随着泡沫铝夹芯板厚度的增加出现“滞后”效应。
c.单位面积吸收能量的多少与破片侵彻深度呈负相关,单位面积吸收的能量越多,破片的侵彻深度越小。采用单位面积吸收的能量这一参数可以更加直观地评估泡沫铝夹芯板抵抗破片侵彻能力的最佳层数。

