基于IV-IOE-LR耦合模型的滑坡易发性评价——以云南省泸水市为例*

陈 羽,杨海林,钟延江

(1.昆明理工大学 国土资源与工程学院,云南 昆明 650093;2.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650000)

0 引言

滑坡灾害具有突发性强、发展迅速、危害性大等特点[1],一旦发生将对附近区域人民生命财产安全造成巨大威胁。滑坡易发性评价是预测滑坡风险的重要手段[2],有利于提高当地滑坡风险的管控水平。

目前,滑坡易发性评价方法分为定性分析和定量分析两类[3]。定性分析需要丰富的野外经验和扎实的理论基础,主观性强,常用方法有专家打分法[4]、层次分析法[5]等;定量分析是利用数理统计学原理进行数据分析,属于数据驱动型方法。常用的数理统计方法有熵值法[6](Index of Entropy,IOE)、频率比法[7](Frequency Ratio,FR)、信息量法[8](Information Value,IV)、确定性系数法[9](Certainty Factor,CF)、证据权法[10](Weight of Evidence,WOE)、逻辑回归法[11](Logistic Regression,LR)、支持向量机[12](Support Vector Machines,SVM)、随机森林[13](Random Fores,RF)等。不同的评价方法有其优势与弊端[14],大量研究证明,耦合模型的精度相较单一模型具有明显优势[15-18]。数理统计模型通过独立比较评价因子与滑坡分布的关系计算因子分级对应的权重,但各孕灾因子之间对于滑坡相对重要性并不明确[19],通过耦合模型计算权重,其优势在于增强了指标权重的客观性[20],弥补了单一方法的缺陷,提高了预测的准确性[21]。信息量模型由于其物理意义明确、操作简单,在滑坡易发性评价研究和实践中得到了广泛应用,但其也存在一定的局限性。熵权法作为一种客观赋权方法,可以根据各因素信息量的分散程度计算各因素的熵权,并对信息量进行合理修正,从而得到较为客观的信息量加权值。逻辑回归作为一种常见的多重线性回归分析模型,其计算量仅与特征数目有关,能根据信息量值通过分类算法快速拟合出各评价因子的类概率回归系数,同样也能弥补原始数据自身缺陷造成的偶然性误差,在滑坡易发性评价研究中已取得良好的应用效果,如:张志沛等[22]基于IOE与IV模型,提出了一种新的加权信息量模型(WIV),其训练精度与预测精度均优于单一模型;田钦等[23]以江西省宁都地区为例,研究发现IV-LR耦合模型不仅继承了单一模型的优势,且精度与分区效果更好;李利峰等[24]在陕西省蓝田县的滑坡易发性评价研究中发现IOE-LR耦合模型精度更高。但目前少见将上述3种模型进行耦合的研究。

本文选取滑坡灾害高发的云南省泸水市作为研究区,结合该区域地质条件与灾害发育规律,选取坡度、高程、曲率、地形起伏度、河流缓冲区、道路缓冲区、年均降雨量、岩组类型和坡向等9个评价指标,将IV、IOE、LR进行耦合得到IV-IOE-LR耦合模型,并与IV、IV-IOE、IV-LR模型进行精度对比,以检验IV-IOE-LR耦合模型在研究区的适用性和可靠性。

1 研究区概况及数据源

1.1 研究区概况

云南省怒江傈僳族自治州泸水市位于北纬25°33′～26°32′、东经99°34′～99°09′之间,地处横断山脉高山峡谷区南端,北高南低,怒江由北向南流经市境长109.6 km,西接高黎贡山,东接碧洛雪山,形成独特的“V”形地貌。泸水市地处欧亚板块与印度板块交界处,印度板块在第三纪与欧亚板块发生了碰撞,并向下俯冲,造成了一系列大断裂和断裂带。境内有20多条河流,分别属于怒江和伊洛瓦底江两大水系。区域地层岩性复杂,软岩、较软岩及地表残坡积层分布区是发生滑坡的主要地段。研究区地理位置以及滑坡点分布见图1。

图1 滑坡点分布

1.2 数据来源

基于野外调查以及收集的地质资料,本文用于滑坡易发性评价的数据主要有:①泸水市30 m分辨率DEM矢量图以及1∶50 000泸水市地形图,用于提取坡度、高程等地形信息;②1∶50 000泸水市地质图经矢量化处理后得到的泸水市岩组类型图;③通过91卫图助手得到的泸水市路网图和河网图;④降雨量数据由泸水市气象数据经克里金插值法计算获得。

2 滑坡易发性评价模型

2.1 信息量(IV)模型

信息量模型是一种基于信息熵的概念来分析各种评价指标下滑坡易发性的模型,现多被用于地质灾害评价,其是根据研究范围内各评价因子信息量值来预测滑坡发生概率的,信息量值越大,滑坡发生概率就越大[25]。信息量模型按以下公式计算:

(1)

(2)

式中,I(xi,H)表示评价因子xi对滑坡事件H提供的信息量,Ni表示滑坡落在评价因子xi范围内的个数,N表示研究区内滑坡总数,Si表示研究区内含有评价因子xi的单元数,S表示研究区评价单元总数,I表示所有评价因子对滑坡所提供的信息量值。

2.2 熵指数模型(IOE)

熵权法是一种基于信息熵理论的客观赋权法,其通过各因素的变异程度来计算各因素的权重[26]。熵指数越大表示该评价因子所占权重越大。但由于评价因子数据类型不一,因此在对信息量赋权之前应将求得的信息量值作归一化处理,以保证数据的规范性和有效性,提升评价模型的精度,计算公式为

(3)

式中,Ih为归一化后的信息量值,Iimin为加权后亚级影响因子最小信息量值,Iimax为亚级影响因子最大信息量值。

将数据归一化处理后,熵权值的计算公式如下:

(4)

(5)

(6)

Hjmax=log2Sj,

(7)

(8)

(9)

Wj=Ij+Hi,

(10)

式中,i为评价因子,j为评价因子分级,b为评价因子分级内滑坡数与总滑坡数的比值,a为对应评价因子分级面积与研究区总面积的比值,FRij为概率比率,Pij为频率密度,Hj和Hjmax为熵值,Sj为影响因子的分类数,Ij为熵权值,Wj为整个因子的合成权重。

2.3 逻辑回归模型(LR)

由于逻辑回归模型允许独立变量的离散或连续,因此被广泛应用于滑坡敏感性的评估。逻辑回归算法与一般线性回归算法的不同之处在于可以用Sigmoid函数将输出约束在[0,1]。当输出为0时,不会发生滑坡;当输出为1时,发生滑坡。因此可以引入阈值的概念对输出结果进行重新分类[27],计算公式为

Z=β0+β1x1+β2x2+…+βnXn,

(11)

(12)

式中:Z为中间变量参数;β0,β1,…,βn为逻辑回归系数;x0,x1,…,xn为滑坡影响因子;P为滑坡发生概率的回归预测值。

3 评价单元及因子的选择

3.1 评价单元选择

本文采用栅格单元评价方法,最佳栅格大小根据李军等[28]提出的一种经验公式计算得到:

Gs=

7.49+0.000 6S-2.0×10-9S2

+2.9×10-15S3,

(13)

式中,Gs为最佳栅格大小,S为地形图比例尺分母。

经计算,Gs理论值为32.853,故本研究取整后采用30 m×30 m分辨率的栅格单元作为最小评价单元。

3.2 评价因子选取

滑坡的形成经历了一个极其复杂的过程,除了受内在因素的控制作用以外,还与人类的工程活动有着密切联系。本文基于前人的研究成果,结合现场地质调查,选取地形地貌、水文环境、基础地质、人类工程活动四大类的10个评价因子构建泸水市滑坡易发性评价指标体系。其中,地形地貌因子有坡度、高程、曲率、地形起伏度、坡向,基础地质因子有岩组类型、断裂缓冲区,水文环境因子有河流、年均降雨量,人类工程活动影响因子有道路。本文结合评价因子的自身特点,利用等间距分级的方法将评价因子分为不同等级。

泸水市滑坡易发性评价因子分级情况见表1,评价因子分级图见图2。

表1 泸水市滑坡易发性评价因子分级情况

3.2.1 地形地貌因子

1)高程

对于相同的坡度而言,坡高越大失稳的可能性就越大[29]。研究区的高程范围在688～4 132 m,将其分为688～1 500 m、1 500～2 400 m、2 400～3 200 m、>3 200 m四个区间(见表1)。由表1可知,研究区高程在688～1 500 m以及1 500～2 400 m之间,其信息量值分别为0.789 4和0.561 1,滑坡发生的可能性最大。

2)坡度

坡度与滑坡的发生有着密切联系,是造成滑坡的重要原因。将研究区的坡度依次分为0°～20°、20°～40°、40°～60°、>60°四个区间(见表1)。由表1可知,滑坡多发生于坡度为0°～20°的区域,此区间内信息量值最大。一般来说,坡度越大,坡体越不稳定,滑坡发生的可能性就越大。现场勘察结果显示,坡度较小的坡面,其斜坡岩体风化程度较高、岩石破裂,坡度大的斜坡岩体节理不发育、稳定性较好。

3)曲率

曲率大于 0 的地方为凸形地貌,曲率小于 0 的地方为凹形地貌,坡体的曲率对坡面物质的运输和沉积有一定影响[30]。将研究区曲率分为<0°和>0°两部分(见表1)。由表1可知,当曲率<0°时,信息量值大于0,表明对滑坡的发生具有正向的促进作用。

4)地形起伏度

地形起伏度是指在特定地区最高、最低高度之间的差异,其反映了地表的起伏特性[31]。将地形起伏度分为0～30 m、30～50 m、50～80 m、80～314 m四个区间(见表1)。由表1可知,研究区的地形起伏度在0～30 m范围内的信息量值最大,表明滑坡发生的可能性最大。

5)坡向

坡向的不同,会造成太阳辐射量的不同,进而影响到水文状况和岩石的风化程度[32]。研究区坡向分为平面、北、东北、东、东南、南、西南、西、西北、北10个等级(见表1)。由表 1可知:在坡向为南的范围内,其信息量值最大,表明最有利于滑坡的发生;而在坡向为西北的范围内,其信息量值最小且为负,表明最不利于滑坡的发生。

3.2.2 基础地质因子

1)岩组类型

岩组类型是滑坡发生的物质基础,将研究区的岩组类型按照软硬程度和厚度分为9个等级(见表1)。由表1可知,研究区内砂砾岩、中细砂双层土体信息量值最大,表明滑坡发生的可能性最大;块状-整体偏硬花岗岩、辉长岩岩组信息量值最小,最不利于滑坡的发生。

2)断裂缓冲区

研究区内断裂发育明显,构造复杂,主要断裂有片马断裂、怒江断裂、田米断裂、称戛断裂、 大兴地断裂等。滑坡主要发生在断层构造密集区域,具有沿构造方向分布的特征[33]。将研究区的河流按 200 m 等步长作缓冲区分为0～300 m、300～600 m、600～900 m、900～1 200 m、1 200～1 500、>1 500 m 六类(见表1)。由表 1可知,在研究区0～300 m范围内,其信息量值最大,表明最有利于滑坡的发生。

3.2.3 水文环境因子

1)河流缓冲区

河流水系对两岸有一定的浸润作用,浸润使岩土体含水率升高,离河流越近的岩土体,越易造成滑坡。将研究区的河流按 200 m 等步长作缓冲区分为0～200 m、200～400 m、400～600 m、600～800 m、800～1 000 m、>1 000 m 六类(见表1)。由表1可知,在研究区0～200 m范围内,其信息量值最大,表明最有利于滑坡的发生。

2)年均降雨量

降雨是造成滑坡的一个重要外部因素,原因是降雨所产生的水流压力使斜坡的抗滑力降低[34]。在降雨作用下,由于水流的冲刷,使坡体崩解泥化,坡面软化,强度下降,最终导致滑坡的发生。将研究区年均降雨量分为1 000～1 400 mm、1 400～2 000 mm、2 000～3 000 mm、3 000～4000 mm、>4 000 mm五类(见表1)。由表 1可知,在1 000～1 400 mm范围内,其信息量值最大,表明滑坡发生的可能性最大。

3.2.4 人类工程活动影响因子

近年来,人类工程活动频繁,尤其是道路修建时因破坏了坡体的平衡状态,导致滑坡频发。将研究区的道路按 200 m 等步长作缓冲区划分为0～200 m、200～400 m、400～600 m、600～800 m、800～1000 m、>1 000 m六类(见表1)。由表1可知,在研究区0～200 m范围内,其信息量值最大,表明最有利于滑坡的发生。

图 2 各评价因子分级图

3.3 评级因子独立性检验

为了确保滑坡易发性评价的各项指标符合模型的要求,必须对各因素进行独立性检验,排除相关系数高的因素。通常认为,相关系数绝对值愈大,二者的关联度愈高,而绝对值低于0.3,则可视为彼此独立[35]。

本文基于SPSS双变量相关性分析获得各因子之间的相关系数(见图3)。由图3可知,高程、地形起伏度、坡度、坡向、断裂缓冲区等10个评价因子之间相互独立,均不存在多重共线性,可纳入评价模型。

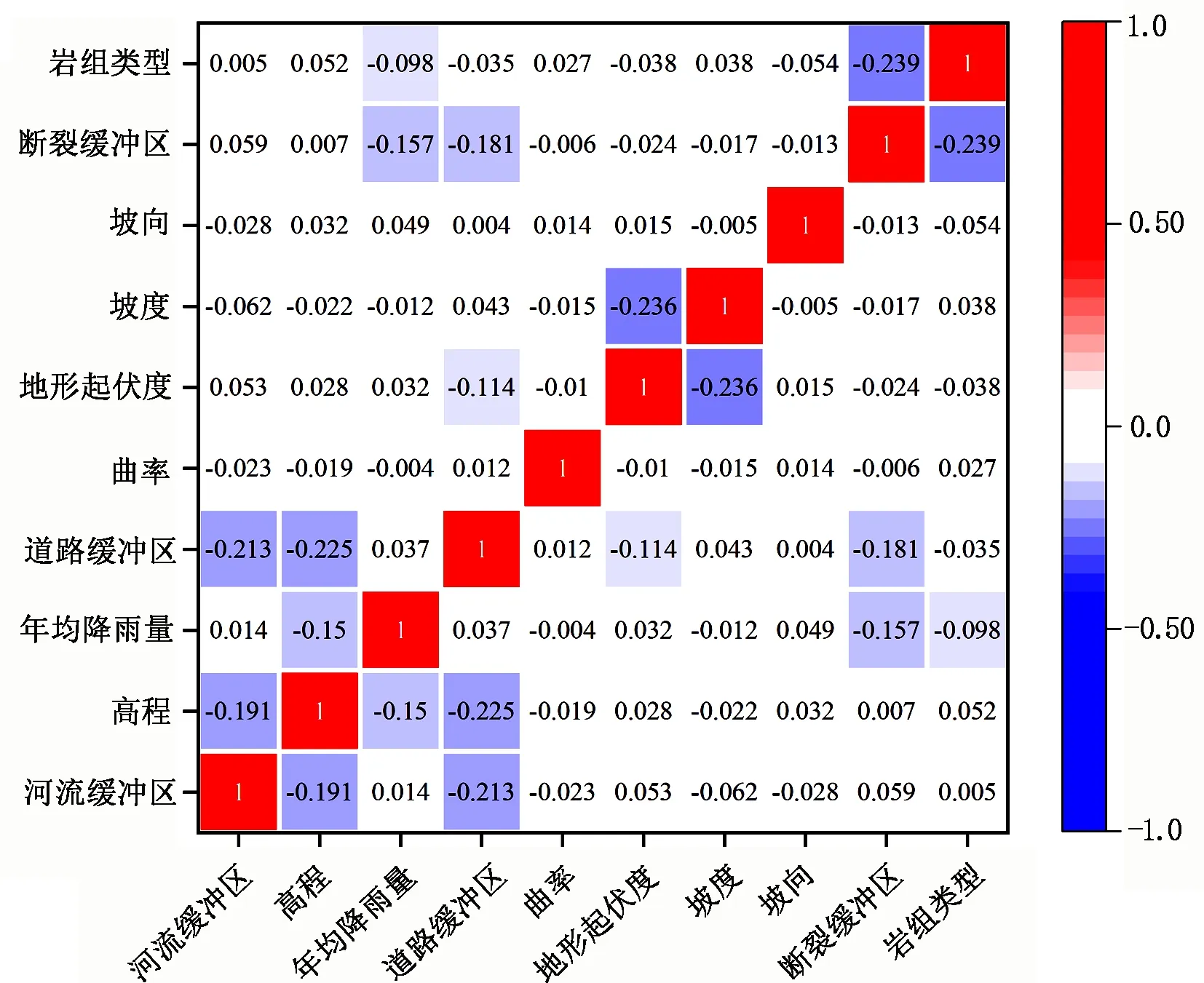
图 3 评价因子相关系数热图

4 滑坡易发性评价及精度分析

4.1 泸水市滑坡易发性评价

4.1.1 基于IV模型的滑坡易发性评价

利用式(1)-式(2)计算指标因子各分级状态下的信息量值,结果见表1。为了使数据更加规范,将其信息量值作归一化处理,应用GIS栅格叠加分析与重分类工具将滑坡的易发区分为极高易发区(6.555～9.5)、高易发区(3.88～6.54)、中易发区(2.09～3.87)、低易发区(0.07～2.08)四个区域(见图4)。

4.1.2 基于IV-IOE耦合模型的滑坡易发性评价

在IV模型的基础上,按照式(3)-式(10)计算得到经熵权法加权后的泸水市滑坡易发性信息量值(见表1)。根据加权信息量值的大小,利用GIS栅格叠加分析和重分类工具将其划分为极高易发区(8.52～12.17)、高易发区(5.80～8.51)、中易发区(2.96～5.79)和低易发区(0.04～2.95)四个等级(见图4)。

4.1.3 基于IV-LR耦合模型的滑坡易发性评价

首先将169个滑坡灾害面文件转为30 m×30 m的栅格文件,并将滑坡栅格赋值为1,非滑坡栅格赋值为0,与因子状态矩阵合并为研究区属性矩阵。在属性矩阵中随机选择与滑坡点数量相同的非滑坡点构建逻辑回归预测样本,导入SPSS软件,选取滑坡点与非滑坡点各70%作为训练集,其余作为验证集,并以初始信息量值为自变量,是否滑坡为因变量进行逻辑回归分析,最终得到IV-LR耦合模型每个评价因子的逻辑回归系数。回归分析中显著性水平≤0.05,表明评价因子具有数理统计意义。由于在IV-LR模型中进行逻辑回归运算时年均降雨量和坡度的显著性分别为0.22和0.175,因此将其剔除。最终IV-LR耦合模型计算公式为

PIV-LR=1/(1+EXP(-(1.112×I1j+0.153×I2j

-0.067×I3j+0.362×I4j+0.502×I5j+0.711

×I6j+0.473×I7j+0.564×I8j-1.247))),

(14)

式中,I1j-I8j分别代表高程、曲率、地形起伏度、坡向、岩组类型、断裂缓冲区、河流缓冲区、道路缓冲区不同等级的信息量值。

根据式(14)得到IV-LR耦合模型的滑坡易发性概率分布图,利用自然间断法将泸水市划分为极高易发区(0.70～0.86)、高易发区(0.40～0.69)、中易发区(0.26～0.39)和低易发区(0.06～0.25)四个等级(见图4)。

与单一信息量模型相比,两种方法耦合评价模型在高易发区和低易发区的预测精度均有较大提高,说明耦合模型的评价效果优于单一模型。

4.1.4 基于IV-IOE-LR耦合模型的滑坡易发性评价

将IV-LR耦合模型中的预测样本导入SPSS软件,训练集与验证集比例为7∶3,以IV-IOE耦合模型的加权信息量值为自变量,同样以是否滑坡为因变量进行逻辑回归分析,最终得到IV-IOE-LR耦合模型各评价因子的逻辑回归系数。

由于在IV-IOE-LR模型中进行逻辑回归运算时地形起伏度的显著性大于0.05,因此剔除地形起伏度影响因子,最终IV-IOE-LR耦合模型计算公式为

PIV-IOE-LR=1/(1+EXP(-(0.709×I1j″+0.522

×I2j″+0.3×I3j″+0.553×I4j″+0.452×I5j″

+0.436×I6j″+0.674×I7j″+0.249×I8j″

+0.3×9jI″-2.578))),

(15)

式中,I1j″-I9j″分别代表高程、坡度、曲率、坡向、岩组类型、断裂缓冲区、河流缓冲区、年均降雨量、道路缓冲区不同等级熵指数加权后的信息量值。

基于式(15),利用GIS栅格计算器得到泸水市滑坡发生概率,利用自然断点法,将其分为极高易发区(0.77～0.94)、高易发区(0.47～0.76)、中易发区(0.27～0.46)和低易发区(0.05～0.26)四个等级(见图4)。

图 4 四种模型滑坡易发性评价结果

4.2 ROC曲线精度分析

受试者工作特征曲线(ROC曲线)是根据一系列不同的分类方式,以真阳性率(敏感度)为纵坐标,假阳性率(1-特异性)为横坐标绘制的曲线,能够更加全面、客观地分析评价体系[36]。AUC(Area Under Curve)为 ROC 曲线下与坐标轴围成的面积。当AUC值为0.7～0.9时,表明模型精度较高;当AUC值大于0.9时,表明模型精度极高。利用SPSS软件对每一种模型的易发性概率和是否滑坡的实际状况进行分析,AUC值越大,模型精度越高,成功率ROC曲线见图5。检验结果表明,IV模型、IV-LR、IV-IOE、IV-IOE-LR耦合模型的AUC值分别为0.764、0.781、0.881、0.829,表明4种模型评价结果与实际情况有着较高的一致性,均对泸水市滑坡易发性作出了较为准确的评价,4种模型的评价精度排序为:IV-IOE-LR>IV-IOE>IV-LR>IV,与单一模式相比,耦合模型的评价精度更高,其中IV-IOE-LR耦合模型评价精度最高。

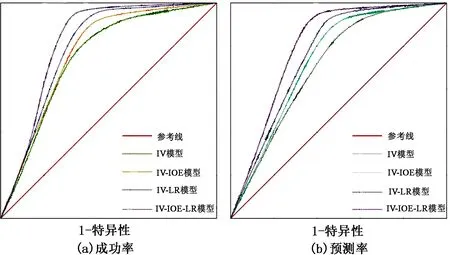
图5 ROC曲线

对未参与训练的30%滑坡栅格进行精度预测分析,预测率ROC曲线见图5。由图5可知:IV、IV-LR、IV-IOE、IV-IOE-LR模型的AUC值分别为0.725、0.736、0.741、0.794,表明4种模型的预测效果良好,IV-IOE-LR模型较IV、IV-LR、IV-IOE模型预测成功率分别提高了9.5%、7.9%、7.2%,IV-IOE-LR模型预测成功率最高。

4.3 评级结果分析

IV-IOE-LR模型中研究区滑坡极高易发区面积为321.71 km2,高易发区面积为902.82 km2,中易发区面积为902.82 km2,低易发区面积为321.71 km2,极高和高易发区主要分布在怒江、芭蕉河、木楠河、以火洛河、腊门嘎河、老窝河、玛布河、赖茂河、石岗河、蛮蚌河、丙贡河、弯桥河、蛮英河等大型河流两岸,以及工程建设密集、人类活动强烈的区域。

5 结论

本文选取高程、坡度、曲率、地形起伏度、坡向、岩组类型、断裂缓冲区、河流缓冲区、年均降雨量、道路缓冲区等10个影响因子构建泸水市易发性评价指标体系,应用 IV、IV-IOE、IV-LR、IV-IOE-LR等模型进行滑坡易发性评价,得到以下主要结论:

a.选取高程、坡度、曲率、地形起伏度、坡向、岩组类型、断裂缓冲区、河流缓冲区、年均降雨量、道路缓冲区等10个影响因子作为评价因子,通过SPSS软件得到各影响因子之间的相关系数,发现均小于0.3,说明影响因子之间不存在共线性,评价因子选择是合理的。

b.通过将IV模型和LR模型及IOE模型相结合,可以很好地克服信息量模型主观性较高的缺点,IV模型、IV-LR、IV-IOE、IV-IOE-LR耦合模型ROC曲线的成功率AUC值分别为0.764、0.781、0.881、0.829,IV-IOE-LR耦合模型效果最好,精度最高。IV、IV-LR、IV-IOE、IV-IOE-LR模型预测率ROC曲线AUC值分别为0.725、0.736、0.741、0.794,IV-IOE-LR耦合模型预测效果最好。

c.IV-IOE-LR耦合模型评价结果表明:极高易发和高易发区均主要分布在怒江、芭蕉河、木楠河、以火洛河、腊门嘎河、老窝河、玛布河、赖茂河、石岗河、蛮蚌河、丙贡河、弯桥河、蛮英河等大型河流两岸,以及工程建设密集、人类活动强烈的区域。