基于模糊物元模型的中深孔爆破布孔优化研究*

李正国,陈星明,粟登峰,陈帮洪,贾凯跃

(西南科技大学 环境与资源学院,四川 绵阳621000)

0 引言

无底柱分段崩落采矿法具有结构简单、安全高效和成本低的突出优点,在地下开采中得到了广泛应用[1]。无底柱分段崩落法多采用扇形中深孔爆破,如爆破参数选取不合理,往往会导致眉线破坏、大块率高、悬顶、推排等问题,进而影响出矿量,并使矿石损失贫化。因此,研究合理的扇形中深孔爆破参数具有重要的现实意义。

周宗红等[2-3]对采场落矿存在的问题及原因进行了分析,优化了采场结构参数和落矿参数,并加强了中深孔质量管理,改进了爆破工艺,有效解决了中深孔落矿存在的眉线破坏严重、装药困难、大块率高等问题;赵彬等[4-5]将BP神经网络技术应用于凿岩爆破参数优选中,可以较好地解决少数据、贫信息、不确定性等问题;殷锦训等[6]运用ANSYS/LS-DYNA数值模拟软件对不同孔网参数的中深孔爆破过程进行了数值模拟计算,确定了三鑫金铜矿扇形中深孔爆破最优排间距为1.4 m、最优孔底距为2.1 m;李斌等[7]应用AUTODYN软件对中深孔爆破进行了数值模拟,提出了改善程潮铁矿无底柱分段崩落法爆破落矿大块率偏高问题的措施。

目前对于中深孔扇形炮孔的优化方法主要有现场实验、非线性预测模拟和数值模拟等。模糊物元模型在决策过程中具有客观、可靠并能减少评价中人为主观因素的影响等优点。贾楠等[8]认为爆破效果评价体系是多元、复杂且具有模糊特性的,其将模糊物元理论与IFAHP 法有机结合并应用于露天采场爆破实例分析中,取得了较为理想的评价效果。史秀志等[9]将信息熵理论与模糊物元理论相结合,建立了基于熵权的城市岩体爆破方案优选的模糊物元评价模型,得出了评价样本与评价标准之间的远近关系与实际情况相符的结论。罗毅等[10]将AHP法、信息熵理论及模糊物元相结合,为台阶爆破方案的合理选择提供了技术支持。模糊物元模型相较其他优选方法简单明了,更加适合于计算机编程[11]。因此,本文提出了一种基于模糊物元模型与数值模拟相结合的爆破参数优化综合评价方法,根据某矿实际条件确定出不同中深孔爆破参数的优化方案,利用ANSYS/LS-DYNA模拟研究了不同方案的岩石爆破效果,最后结合数值模拟结果采用模糊物元模型对爆破方案进行优选。

1 矿山概况

某矿采用无底柱分段崩落法采矿,矿体节理裂隙较为发育且易凿易爆,目前单排中深孔炮孔数目达到了11个,单排装药量为450～500 kg,单耗为0.4 kg/t,爆破后出现了大块和粉矿严重的两极分化现象,此外推排和悬顶事故也偶有发生,对矿山生产作业产生了较大影响。 11孔爆破方案见图1,现场爆破情况见图2。

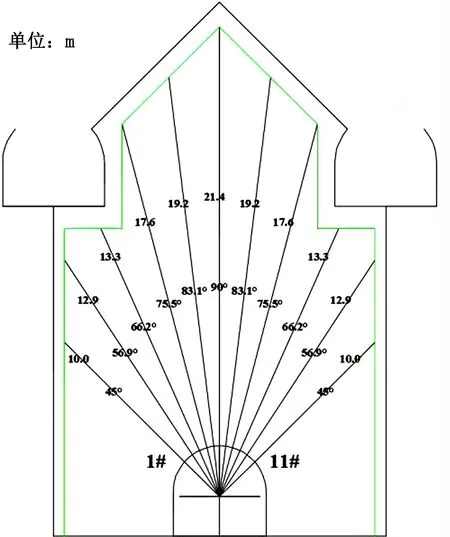
图1 11孔爆破方案

当单个中深孔排面炮孔数目为11个时,扇形中深孔爆破效果较差,需要对中深孔爆破参数进行优化。以改变扇形炮孔数目为出发点,根据进路掘进揭露的岩性好坏以及前期生产经验,拟将炮孔数从11个减少至7～10个,由此提出了7孔、8孔、9孔和10孔爆破方案,孔径78 mm,排面边孔角取45°,采用单放射中心方式凿岩,炮排爆破边界距扇形设计排面边界0.5～0.8 m,崩矿步距2.2 m。9孔爆破方案见图3,各方案炮孔参数见表1。

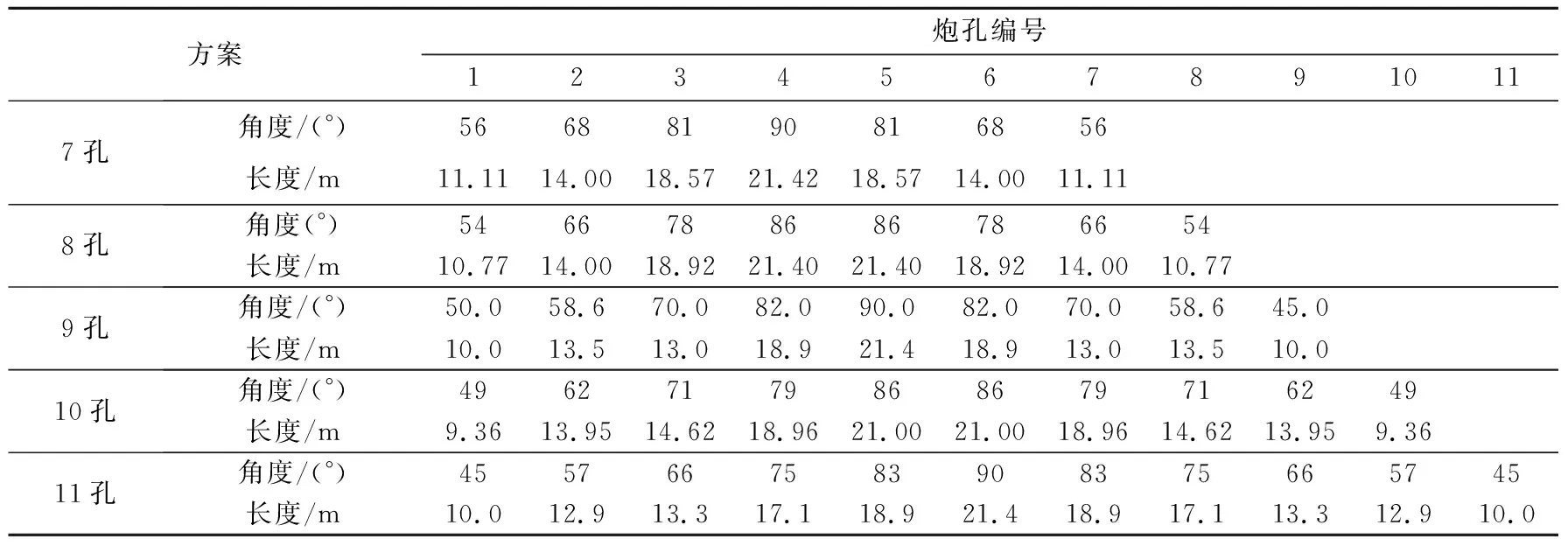
表1 各方案炮孔参数

2 数值模拟

2.1 数值计算模型

根据提出的7、8、9、10孔爆破方案,连同11孔爆破方案,一共建立5组数值计算模型。以9孔模型为例,采用准三维模型建模[6],边界条件设为无反射边界,模拟无限大空间,单元网格尺寸为0.05 m×0.05 m×0.05 m,求解时间设置为2.5 ms。假设矿岩为均匀介质,不考虑其内部裂隙和损伤,爆炸应力均匀分布。几何模型尺寸与边界设置见图4。

图4 几何模型尺寸和边界设置

孔底区域应力波作用时间最短,破碎效果最差,因此选取两相邻炮孔孔底连线的中心作为观测点,如图5中的A、B、C、D、E、F、G、H八个观察点,用来观测孔底区域爆破后的有效应力。

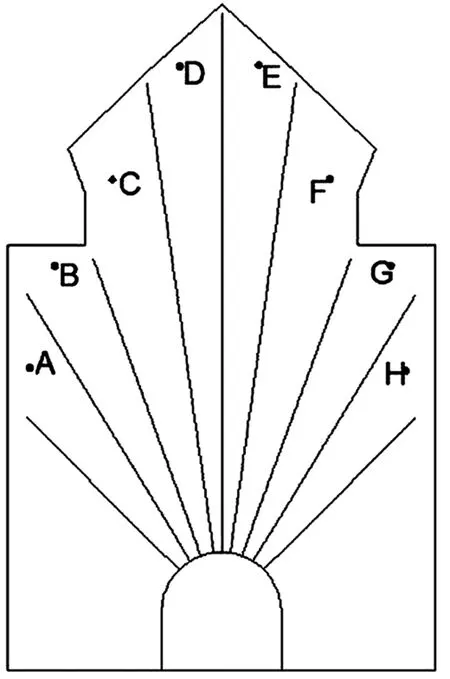
图5 观测点位置

图6为几何模型和桃形矿柱局部网格放大图。

图6 几何模型和桃形矿柱局部网格放大图

2.2 材料参数选择

2.2.1 矿石材料模型

炸药爆炸时近区岩体发生屈服以致破碎,矿岩一般在大应变、高应变率、高压的条件下遭到破坏,采用包含应变率的塑性随动模型是比较合适的[12],其关键字定义为*MAT_PLASTIC_KINEMATIC,矿石材料参数见表2。表2中,β=1表示模型采用各向同性硬化,C表示应变率参数。

表2 矿石材料参数

2.2.2 炸药材料模型

矿山采用乳化炸药进行爆破作业,模拟起爆顺序为孔底同时起爆,材料模型选用高能炸药模型[13],关键字定义为*MAT_HIGH_EXPLOSIVE_BURN,采用JWL状态方程模拟炸药爆轰过程中压力P和爆轰体积V之间的关系:

(1)

式中,A为材料的初始屈服应力,B为应变硬化模量,R1、R2、ω为常数,E0为初始内能密度。炸药材料参数及状态方程参数见表3。

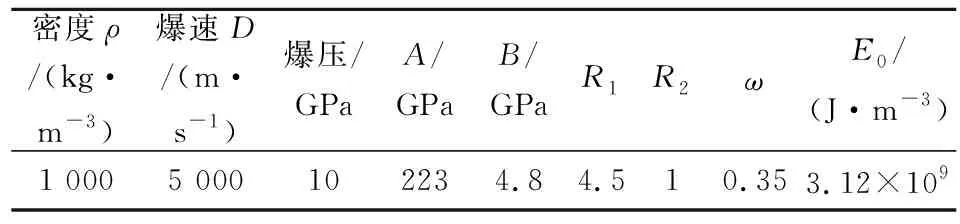
表3 炸药材料参数及状态方程参数

2.2.3 材料失效准则

根据相关研究[14],本文采用von Mises屈服准则判断矿岩是否发生破坏。在爆破模拟过程中,对爆破排面不同位置监测单元不同时刻的von Mises时程曲线进行分析,当监测位置的网格单元所受等效应力大于岩石动态抗压强度时,即认为矿岩发生破坏。岩石的动态抗压强度计算式为

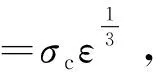
(2)

式中:σ压为岩石的动态抗压强度;σc为岩石的静态单轴抗压强度;ε为岩石的加载应变率,根据矿山资料,岩石的加载应变率取190 s-1。

根据矿山已有的矿岩力学试验结果,可得矿岩的动态抗压强度为270 MPa。

2.3 模拟结果分析

2.3.1 爆炸应力波演化规律

对7、8、9、10、11孔爆破模拟结果的分析可知,不同孔数爆破时其爆炸应力波的传播规律大致相同。因此,本文着重对9孔爆破时的爆炸应力波传播规律进行分析。图7为9孔爆破时爆炸应力波演化云图。

由图9可知:炸药起爆后会在矿岩中形成爆炸应力波并向四周传播;在爆炸应力波向孔口方向传播过程中,相邻炮孔所产生的爆炸应力波会在相交位置发生明显的应力叠加现象;随着爆炸应力波的持续传播,高应力区不断扩大,在孔底部分出现低应力区,且低应力区逐渐从孔底向孔口移动;所有应力波传递到孔口时,炮孔间产生高应力并向四周扩散。由上可知,在爆破过程中孔口和孔底区域均会出现高应力区,而低应力区则主要出现在炮孔底部区域,由于低应力区的峰值应力普遍小于矿岩动态抗压强度,表明爆破大块主要分布在炮孔孔底位置,在放矿时主要出现在中后期,这与现场生产实际相符。

为了更加合理地分析不同数目炮孔爆破效果的优劣,对7、8、9、10、11孔数的测点有效应力时程进行了分析,统计得到不同爆破方案下各监测点的峰值有效应力(见表4)。

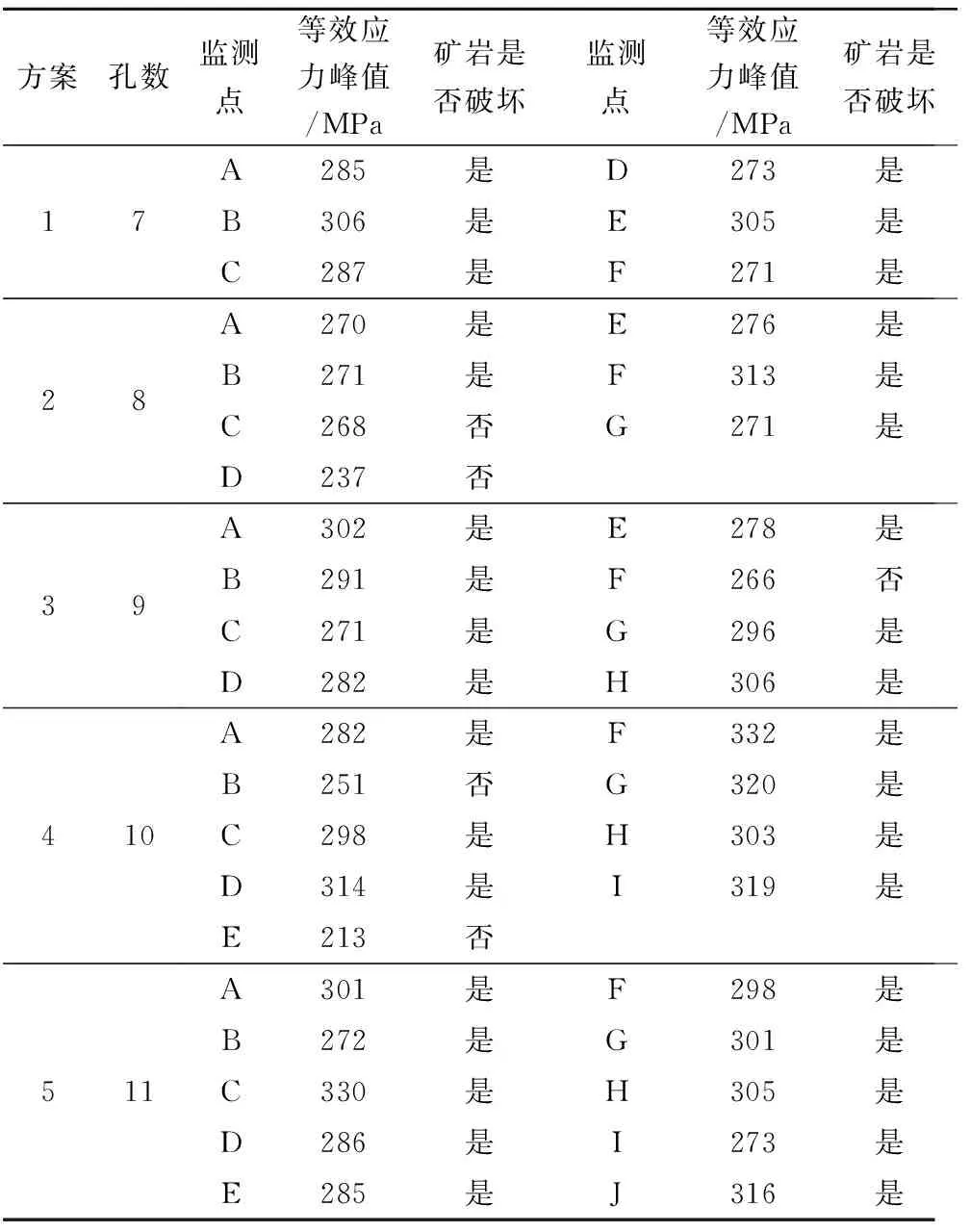
表4 各监测点最大有效应力值

由表4可知,7、11孔方案所有测点的有效应力峰值均超过了矿岩的动态抗压强度,9孔方案只有个别测点有效应力峰值低于矿岩的动态抗压强度,8、10孔方案中有2个测点有效应力峰值低于矿岩的动态抗压强度。

2.3.2 爆生裂纹扩展及矿体破碎特征

本文通过定义单元失效模拟爆生裂纹的起裂扩展及矿岩破碎,各方案的爆生裂纹分布及矿岩破碎效果见图8。该矿山利用直径3 m溜井放矿,溜井口的筛网网格尺寸为500 mm×500 mm,矿石最大横截面积大于筛网单孔面积时即视为大块。当矿石直径小于3 cm时,矿石遇水易黏结,导致溜井堵塞,所以矿石直径小于3 cm的部分视为粉矿。在CAD中统计各方案爆生裂纹图中的大块及粉矿,结果见表5。扇形炮孔爆破时,越靠近孔口位置,由于应力的叠加和装药密度较大,破碎效果越好;而由于孔底炮孔的间距较大,应力波作用时间较短,所以大块较多,破碎效果欠佳。通过对比不同方案的爆破效果可以看出,7孔爆破时,爆生裂纹明显少于其他方案,孔底大块也相对较多,但孔口的破碎效果较好,整体块度较均匀;8孔爆破时,孔底块度较大,尤其是中间两孔孔底;9孔爆破的整体破碎效果较好,孔底部分出现大块,孔口破碎块度较均匀;10孔爆破时,大块较少,由于孔口装药量的增加,在接近孔口的区域矿石较粉碎;11孔爆破时,大块最少,但粉碎区较大。

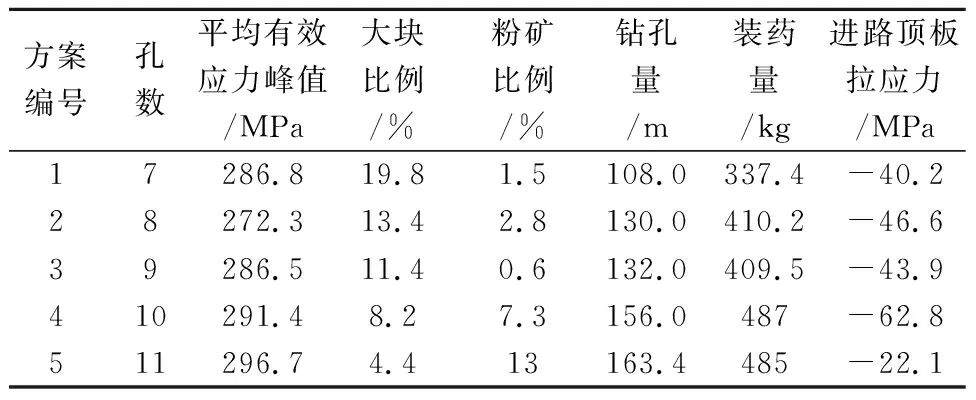
表5 各方案评价指标量值

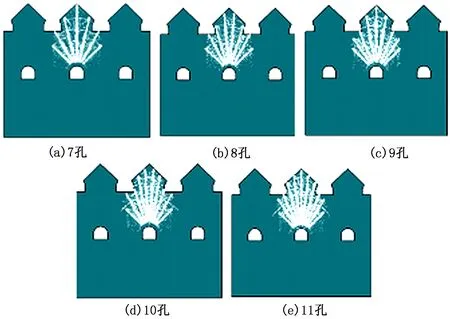
图8 各爆破方案的矿岩破碎效果

综合以上分析可以看出,5种爆破方案矿岩爆破效果各有优劣,采用单一爆破参数优化方法难以客观、准确地对各爆破方案作出评价,因此本文将在以上分析结果的基础上采用变异系数法和模糊物元模型对5种爆破方案进行优选。

3 爆破方案优选

3.1 模糊物元模型

物元分析理论常用于解决工程实际中的不相容问题,物元是由“事物、特征、量值”3个要素组成的有序三元组的基本元,这些元素可被用来描述任一具体事物。其思想是将模糊数学和物元分析的内容有机融合、交叉渗透,分析量值的模糊性和要素间的不相容性,从而解决模糊不相容问题[15]。

3.1.1 模糊物元模型

令评价事物为A,x为特征b对应的量值,组成的有序三元组R=(A,b,x)即为物元。假设事物A有m个特征b1,b2,…,bm,对应的量值具有模糊性,为x1,x2,…,xm,此时R为m维复合模糊物元。m维模糊物元与n个事物组合在一起构成n个事物m维复合模糊物元Rn×m[16],记作

(3)

式中,xij为第n个事物第m个特征的模糊量值。

3.1.2 隶属度复合模糊物元

利用从优隶属度表示评价指标对应量值的从属程度,其分为效益型指标和成本型指标。

效益型指标:

(4)

成本型指标:

(5)

此时构成m维隶属度复合模糊物元,即

(6)

式中,μij为第n个事物第m个特征的模糊量值,即从优隶属度。

3.1.3 关联系数与复合模糊物元

事物之间的关联性由关联函数确定,关联函数记为ξ(x),在模糊物元模型中已知某一量值xij,则可根据关联函数确定对应的函数值,也称为关联系数,关联系数与隶属度的相互转换称为关联变换。由于关联函数与隶属度等价[17],故关联系数可由隶属度确定,即

ξij=μij(i=1,2,…,n;j=1,2,…,m) ,

(7)

式中,ξij为第n个事物第m个特征的关联系数。

此时,关联系数复合模糊物元记为

(8)

3.2 指标权重确定

采用变异系数法确定指标权重。变异系数法是一种客观赋权法,具体步骤叙述如下。

(1)无量纲化处理

对于效益型指标,有

(9)

对于成本型指标,有

(10)

(11)

(12)

(3)求各指标变异系数

(13)

(4)对变异系数Ej作归一化处理,便得到各指标权重:

(14)

3.3 关联度计算

用关联度衡量事物间的关联性,计算式为

(15)

式中,Ki为第n个事物的关联度,以关联度最大原则确定最优方案。

3.4 方案优选

3.4.1 评价指标选取

采用von Mises屈服准则判断矿岩是否发生破坏,取各方案监测点等效应力峰值的平均值作为指标之一。将统计的各方案大块和粉矿所占比例也作为评价指标。在考虑破碎效果的同时,还应考虑爆破成本,故将炸药量和钻孔量也作为评价指标。顶板中间是最易发生破坏的部位[18],而自由面附近发生的“片落”是岩石所受拉应力超过其抗拉强度所致[19]。由于采用准平面应变模型建模,选取当前排面爆破时的进路顶板拉应力作为评价指标,近似表征后排炮孔眉线破坏情况。

根据数值模拟结果,各方案评价指标量值见表5。

3.4.2 方案优选结果

根据式(3)-式(7)算得隶属度复合模糊物元:

根据式(8)-式(13),用变异系数法求得6个指标的权重:

利用式(14)计算关联度:

由关联度计算结果可知,K3>K5>K1>K2>K4,根据最大方案原则,5个方案优先决策顺序为:方案3>方案5>方案1>方案2>方案4。即扇形炮孔数目为9孔时,爆破效果最佳。

4 结论

本文提出了一种基于模糊物元模型与数值模拟相结合的爆破参数优化综合评价方法,根据某矿实际条件确定了不同中深孔爆破参数优化方案,利用ANSYS/LS-DYNA模拟分析了不同方案的爆破效果,得到以下主要结论:

a.根据数值模拟及现场爆破大块分布规律,低应力区多出现在孔底区域。

b.以数值模拟结果为样本,通过变异系数法和模糊物元模型确定矿山最优的扇形排面爆破中深孔数目为9孔。

c.数值模拟结合变异系数法和模糊物元模型的爆破方案优化综合评价结果更加客观、可靠,减少了评价中主观因素的影响。