垂直溜井贮矿段放矿中矿岩运动速度变化特征
曹 朋 路增祥,2 马 驰 吴晓旭
(1.辽宁科技大学矿业工程学院,辽宁鞍山114051;2.辽宁省金属矿产资源绿色开采工程研究中心,辽宁鞍山114051)
堵塞和井壁磨损变形是影响溜井贮矿段使用效 果的主要原因[1-3]。溜井底部放矿过程中,贮矿段内矿岩物料的运动状态对溜井堵塞、井壁磨损问题产生着重要影响[4-6]。因此,研究矿岩运动状态有助于降低溜井贮矿段堵塞和井壁磨损问题的发生概率,进而提高溜井的矿岩运输效率。
为解决溜井贮矿段的堵塞和井壁磨损问题,王其飞[7]以椭球体理论为基础,通过数值模拟试验,宏观描述了贮矿段内矿岩运移特点。刘艳章等[8-9]、邹晓甜等[10]采用质量流率比评价了矿岩流动状态,并结合数值模拟和物理模拟试验,分析了贮矿高度、含水率、粉矿含量和底部放矿漏斗角对矿岩流动性的影响。结果表明:质量流率比随着贮矿高度、底部放矿漏斗角增加呈现出先增大后减小的趋势,随着含水率增加呈现出先减小后增大的趋势;随着粉矿含量增加呈现出减小趋势。张慧等[11]引入矿岩块度模数概念,通过溜井放矿数值模拟试验发现,矿岩块度模数越大,溜井放矿速率越小,当块度模数超过0.9时,溜井会发生堵塞;矿岩块度均匀分布条件下的矿岩流动性优于高斯分布条件下的矿岩流动性。HADJIGEORGIOU[12]和 HOHNER 等[13-14]总结了悬拱问题的研究现状,并利用离散元数值模拟了溜井放矿过程。研究表明:溜井断面、矿岩形态及其大小以及溜井尺寸与矿岩尺寸的比值是影响溜井放矿过程中矿岩流动性的主要因素。刘永涛等[15]采用BP神经网络,通过物理放矿试验获取数据训练样本,建立了溜井堵塞率预测模型。众多研究发现,溜井断面尺寸[16-17]、贮矿高度[18]、倾斜角度[19]和放矿速度[20]影响着悬拱发生率、贮矿段内矿岩流动性以及矿块大小选择。
上述研究在多个角度下分析了溜井贮矿段内矿岩的运动特征,并且大多侧重于分析各因素对贮矿段物料流动性的影响。溜井中矿岩颗粒间的内摩擦力与细颗粒的黏结阻力,是矿岩流动特性的最主要影响因素,也是溜井产生堵塞的重要原因[6],而矿岩与井壁材料本身硬度以及二者接触时的应力[21-23]、相对速度[8]等指标是评判井壁材料磨损程度的主要因素。目前,围绕溜井问题的研究大多以单位时间内通过放矿口的矿岩质量等指标判定矿岩整体流动性优劣,仅能评判溜井溜口处放矿速度大小,无法作为深入分析井壁磨损、溜井堵塞问题的依据。在了解贮矿段内矿岩颗粒运动速度及其分布特征的基础上,开展井壁摩擦机理和损伤程度分布特征研究,有助于从根本上解决溜井堵塞和井壁损伤破坏问题。本研究通过数值模拟试验,采用时均化分析方法,研究溜井贮矿段放矿过程中矿岩颗粒运动速度的变化特征,以及颗粒位置对矿岩时均速度的影响,结合矿岩运动速度变化规律,讨论溜井筒仓和放矿漏斗井壁磨损程度分布特征和堵塞悬拱率问题,对于解决溜井贮矿段井壁磨损问题和溜井堵塞问题具有一定的参考意义。
1 溜井贮矿段放矿离散元模型
贮矿段矿岩颗粒运动状态具有不可见和不可量测特性,传统物理试验方法无法提供研究所需的试验数据。离散元数值模拟是颗粒散体运动问题的主要研究方法之一。
以垂直溜井贮矿段为试验对象,建立放矿口位于溜井断面中心的贮矿段模型,模拟溜井贮矿段放矿过程。放矿模型由筒仓、放矿漏斗以及井内储料组成。为分析矿岩颗粒速度变化特征,记录放矿过程中矿岩颗粒位移与时间的关系,在试验模型内建立了XOY二维坐标系,如图1所示。
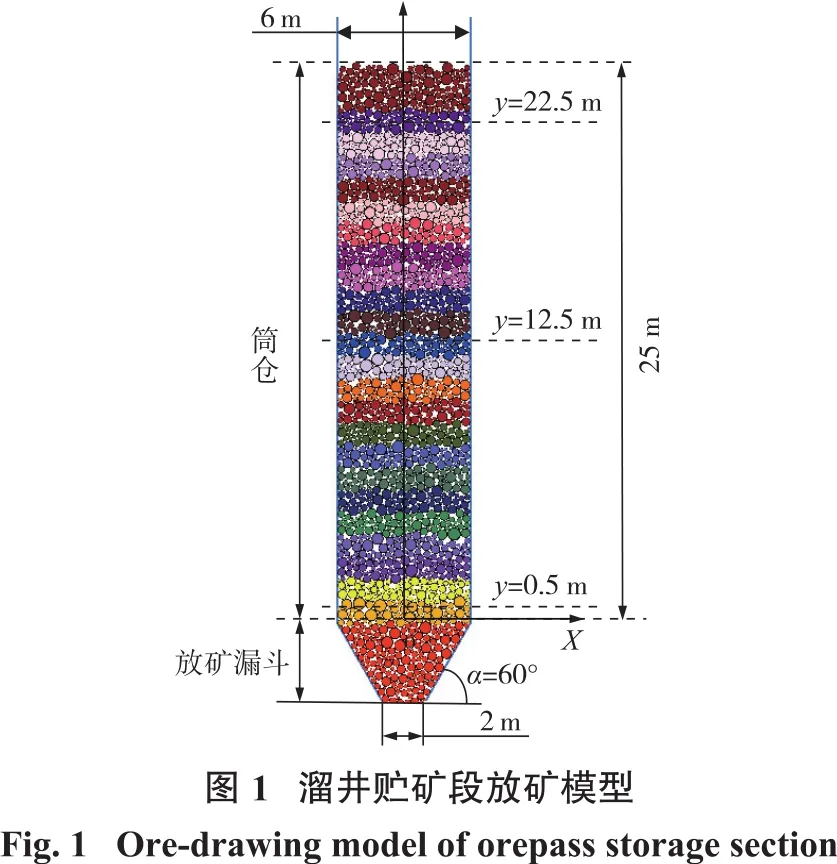
采用球形颗粒模拟矿岩,矿岩级配参数取值见表1[24]。根据现场实际情况,确定颗粒间接触选用Hertz颗粒力学接触模型,球与墙间选用线性接触模型[20,25],所需细观力学参数见表 2。放矿方式、放矿速度会影响溜井内矿岩个体运动速度,本研究重点分析矿岩颗粒速度变化特征,为规避上述两种因素的影响,采用连续放矿方式,即放矿前直接删除溜井底板,放矿口处矿岩自由下落,放矿时不控制单位时间内矿岩放出量。

2 放矿过程速度变化特征
2.1 矿岩整体速度分布特征
放矿过程中矿岩标记带的变化情况能够反映矿岩整体速度分布特征,为便于分析该特征,按照放出矿岩量多少,记录矿岩标记带的形态特征。放矿前矿岩标记带形态、放出1/3矿岩量时矿岩标记带形态和放出2/3矿岩量时矿岩标记带形态如图2所示。

由图2(a)可知:放矿前,矿岩标记带水平布置,上下矿岩标记带间界限清晰。由图2(b)可知:当放出1/3矿岩量时,矿岩标记带形态分别在筒仓和放矿漏斗两部分呈现出差异性较大的两种形态特征:即筒仓部分矿岩标记带形态呈弧形,放矿漏斗部分矿岩标记带形态呈“V”形。在筒仓部分,矿岩标记带形态变化表明,越靠近筒仓中心线的矿岩颗粒下移速度越快,并且随着筒仓标高降低,矿岩标记带界限的弧度略有增大趋势。在放矿漏斗内,矿岩标记带形态变化说明,筒仓部分的矿岩颗粒进入放矿漏斗后下移速度发生了较大变化,即矿岩进入放矿漏斗后,靠近筒仓中心线的颗粒下移速度进一步增大,且远大于靠近井壁的颗粒速度,部分矿岩颗粒会滞留在出矿口两侧边壁上,滞留的矿岩会对上部矿岩颗粒运动产生一定的影响。放出2/3矿岩量时矿岩标记带形态变化与图2(b)一致,如图2(c)所示。
2.2 矿岩颗粒瞬时速度变化特征
为了揭示溜井贮矿段内部矿岩颗粒在放矿过程中的速度变化规律,选取具有代表性的多个矿岩颗粒作为研究对象。结合矿岩标记带形态变化特征分析发现,矿岩颗粒初始标高越大,在溜井内运动的时间便越长,运动过程更加完整;同一平面下矿岩颗粒下移时速度呈现出以筒仓中心线对称分布的特征。选取筒仓中心线左侧同一标高下编号及坐标分别为A1(-2.8,22.5)、A2(-1.4,22.5)、A3(0,22.5)的3个矿岩颗粒进行分析。放矿过程中,编号为A1的矿岩颗粒运动速度随时间的变化曲线如图3所示。

由图3可知:标记带矿岩从其初始位置移动到溜井放矿口总历时20 s,放矿过程中矿岩颗粒的瞬时速度随时间变化呈现出波动性变化形式,根据波峰和波谷的平均值变化趋势,整体上呈现出3种不同的波动形式。0~4 s内矿岩颗粒瞬时速度上下波动幅度与其他时间段相比较大,其波动范围为0~3.32 m/s,波峰和波谷的平均值分别2.55 m/s和0.45 m/s;4.0~16.5 s内矿岩颗粒瞬时速度波动幅度较小,其波动范围为0.03~3.00 m/s,波谷与前一时间段波动幅度基本相似,波峰明显小于0~4 s时间段,波峰和波谷平均值分别为1.99 m/s和0.64 m/s;16.5~20.0 s内矿岩颗粒瞬时速度呈上升趋势,波峰和波谷随时间变化而增大,波谷增幅明显,其平均值为1.11 m/s,大于前两个时间阶段的波谷平均值。
放矿过程中,编号为A2、A3的矿岩颗粒运动速度随时间的变化曲线如图4所示。
对比图3和图4可知:矿岩颗粒A2、A3瞬时速度随时间变化的波动形式与颗粒A1一致,说明矿岩瞬时速度整体波动形式变化具有普遍性。通过对比颗粒A1、A2和A3的瞬时速度变化特征可知,同一高度下横坐标不同的矿岩瞬时速度的振幅变化是不同的,在0~4 s内不同颗粒的波动振幅差异明显,越靠近井筒中心线,矿岩颗粒的波动振幅越小;在放矿4 s之后且矿岩颗粒到达放矿漏斗之前,这段时间内越靠近井筒中心线,矿岩颗粒波动的振幅波动越稳定;到达放矿漏斗后,矿岩颗粒波动剧烈,振幅均呈增大趋势。不同位置下,矿岩颗粒到达放矿漏斗的时间不同。颗粒A1用时18.1 s,颗粒A2和A3分别用时15.6 s和15.4 s,说明越靠近井筒中心线,矿岩颗粒到达放矿漏斗所需的时间越少。

以上分析表明:放矿过程中矿岩颗粒在溜井贮矿段运动的瞬时速度整体变化呈现出周期性的波动形式,表现为0~4.0 s内振幅较大、波峰波谷清晰,4.0~16.5 s内振幅较小、以周期性变化的速度波动,16.5~20.0 s内振幅较大且波峰波谷平均值随时间增加而增大,速度明显呈增长趋势,在放矿漏斗内矿岩颗粒瞬时速度大于该颗粒在筒仓时的瞬时速度。颗粒位置不会影响瞬时速度的波动形式,但会影响矿岩速度的波动幅度及到达放矿口的时间。
3 速度时均化分析
根据图3和图4可知:放矿过程中矿岩颗粒运动经过筒仓部分和放矿漏斗部分的瞬时速度变化形式差异性较大,需分别讨论。为了进一步分析不同部分下矿岩颗粒瞬时速度变化特征,将筒仓和放矿漏斗两部分矿岩颗粒瞬时速度分别进行时均化分析,以直观地揭示矿岩颗粒在放矿过程中的速度变化特征。
3.1 速度时均化分析方法
假设矿岩颗粒初始坐标为(x1,y1),放矿Δt后矿岩坐标为(x2,y2),根据瞬时速度计算公式,则有下式成立:

式中:ΔL为矿岩位移量,m;v为该时刻下矿岩颗粒的瞬时速度,m/s。
在已知不同时刻下矿岩坐标位置信息,t时刻矿岩运动瞬时速度可由下式计算:

通过将运动要素时均化,分析流动单元运动特征是流体力学中研究湍流运动的有效途径之一[24]。参考流体力学中湍流运动分析方法,不考虑散体颗粒运动的随机性,将颗粒运动速度时均化,深入分析颗粒运动的瞬时速度变化特征。
假设矿岩颗粒在某一时刻的瞬时流速为v,t时刻下矿岩颗粒速度为v(t),在T时间内,矿岩颗粒运动速度平均值为,则有:

由矿岩颗粒运动速度与时间的关系曲线可知,矿岩颗粒瞬时速度随时间不断变化,结合湍流运动分析方法以及样本均值、偏差处理方法,可认为这种瞬时流速v是由时均流速和脉动流速v'构成。即,瞬时流速v为脉动流速v'与时间平均流速之和:

通常引用脉动流速的均方根表示脉动幅度大小[26],即脉动强度N为

3.2 矿岩颗粒速度时均化分析
放矿开始0~4 s内矿岩颗粒速度变化幅度较大,该时段颗粒运动过程分析较为困难,因此忽略这一时间段。本研究主要分析矿岩颗粒运动稳定后的速度变化情况,即对4.0~16.5 s(矿岩颗粒经过筒仓部分)和18~20 s(矿岩颗粒经过放矿漏斗部分)这两个时间段矿岩颗粒的瞬时速度变化过程分别进行时均化分析。通过线性拟合获得溜井贮矿段内矿岩颗粒A1经过筒仓部分和放矿漏斗部分的瞬时速度、时均速度与放矿时间的关系曲线如图5所示。
由图5(a)可知:颗粒A1经过筒仓部分时矿岩时均速度为1.233 8 m/s,斜率为0.005 4,脉动强度为1.431 5,矿岩近乎做时均速度恒定的运动。由图5(b)可知:颗粒A1经过放矿漏斗部分时矿岩时均速度为14.427 6 m/s,斜率为0.865 2,矿岩做时均速度随时间增加而增大的运动。
分别对矿岩颗粒A1、A2和A3的瞬时速度进行时均化分析,结果见表3。

注:斜率为加速度;截距为时均速度。
由表3可知:矿岩颗粒在筒仓部分和放矿漏斗部分的瞬时速度时均化结果呈现出明显的差异性。在筒仓部分,不同位置矿岩颗粒的斜率和截距相差不大,时均速度与时间关系曲线近似为一条水平直线;在放矿漏斗部分,矿岩颗粒位置越接近筒仓中心线,时均速度与时间关系曲线的斜率越大,截距绝对值也越大。通过对矿岩颗粒瞬时速度与时间的关系曲线进行时均化分析,结果表明:筒仓部分矿岩颗粒以恒定的时均速度运动,颗粒A1的时均速度略小于其他两个颗粒,颗粒A2和A3的时均速度相差较小。在放矿漏斗部分,矿岩颗粒的时均速度随放矿时间增加而增大,矿岩颗粒所在位置影响时均速度变化特征,呈现出横坐标越靠近筒仓中心线、矿岩颗粒时均速度增长越快的特征。同时矿岩颗粒经过放矿漏斗部分的时均速度明显大于该颗粒经过筒仓部分的时均速度。
3.3 矿岩颗粒瞬时速度变化对溜井问题的影响
在溜井结构参数、井壁与矿岩材料硬度等因素一定的条件下,井壁磨损程度主要受矿岩颗粒与井壁间井壁动态应力[21-23]和相对速度[8]共同影响。本研究根据矿岩颗粒速度时均化分析结果,进一步讨论矿岩颗粒瞬时速度变化对溜井贮矿段堵塞和井壁磨损问题的影响。
(1)“矿岩颗粒在筒仓部分以恒定的时均速度下移”这一特征,反映出在连续放矿条件下,筒仓部分矿岩颗粒与井壁接触时的相对速度是一定的,与标高无关。此时,井壁磨损程度的分布特征是由井壁动态应力决定,磨损特征与井壁应力分布特征[27]一致。在放矿漏斗部分,矿岩的时均速度随时间增加而增大,说明此时井壁磨损程度的分布特征是由矿岩颗粒与井壁间的相对速度和井壁动态应力共同影响。
(2)在筒仓部分不同位置下,矿岩颗粒时均速度恒定且相差较小时,矿岩颗粒呈整体下移趋势,不易发生堵塞问题。
(3)在放矿漏斗不同位置下,矿岩颗粒时均速度差异性较大且随时间增加,矿岩块间相对时均速度相差越大,越容易发生结拱堵塞。
因此,溜井放矿过程中,在放矿漏斗部分发生堵塞的概率大于筒仓部分,同时矿岩块产生悬拱的概率随标高降低而增大。此外,由于溜井底部放矿漏斗边界倾角的影响,存在部分矿岩滞留在放矿漏斗两侧,阻碍上部矿岩运动的现象,进一步增加了溜井悬拱率。
4 结 论
(1)对矿岩颗粒在溜井贮矿段不同时段运动状态的研究发现,矿岩颗粒运动过程中呈整体下移状态,筒仓中心线附近矿岩颗粒下移速度略大于两侧矿岩颗粒下移速度,在放矿漏斗部分时该现象更加突出,并且放矿口两侧滞留的矿岩会影响上部矿岩流动。
(2)矿岩颗粒速度时均化分析研究表明,在贮矿段放矿过程中,矿岩颗粒瞬时速度呈现波动性变化形式,整体表现为筒仓部分,先振幅较大、随后振幅较小且以稳定的速度波动,时均速度为一定值;放矿漏斗部分,振幅较大且波峰、波谷呈明显增加的速度波动,时均速度随时间增加而增大。
(3)溜井筒仓部位的矿岩颗粒时均速度恒定且相差较小时,不易发生堵塞问题;而在放矿漏斗部位,矿岩颗粒时均速度差异性较大,易发生堵塞。
(4)溜井结构参数、放矿时机、放矿速度等因素发生变化也会影响矿岩运移速度,有待于进一步开展研究。

