溜井储矿段矿岩散体运移轨迹及速度预测模型

马 驰，路增祥，殷 越，曹 朋

1) 辽宁科技大学矿业工程学院，鞍山 114051 2) 辽宁省金属矿产资源绿色开采工程研究中心，鞍山 114051

溜井是矿产资源地下开采矿山的重要工程之一，承担着矿岩储存和下向运输任务. 溜井堵塞和井壁的变形破坏等溜井问题严重影响着矿山生产的连续性和安全性[1−2]，给矿山生产带来了较大影响. 根据矿岩在溜井中的运动特征，溜井井筒可分为溜矿段和储矿段两大部分，这两部分井壁的变形破坏机理与特征表现出较大的差异. 矿岩在溜井内的运动过程中与井壁接触并产生力的作用，是导致溜井井壁破坏的主要原因之一[1]，而运动过程中矿岩颗粒之间的相互作用又是产生溜井堵塞的重要原因之一[2]. 目前针对溜井储矿段问题的研究大都聚焦于分析溜井围岩稳定性[3]、探究溜井堵塞、井壁磨损问题的发生原因及解决办法[4]等方面，而涉及堵塞、磨损问题发生机理方面的深层次研究较少且进展缓慢[2]. 溜井储矿段中矿岩运移状态的不确定性，导致了溜井储矿段堵塞频率[5]、井壁磨损程度[6]也不相同. 因此，研究溜井储矿段内矿岩运移规律，定量矿岩运移过程中的轨迹和速度变化，是揭示溜井储矿段中堵塞和井壁磨损等问题发生机理的重要研究方向.

矿石在储矿段内运动状态具有不可量测性，因而很难通过常规手段得到矿石在溜井储矿段内的运移特征. 目前的研究大多以椭球体放矿理论为基础，宏观推测矿岩运移规律. 早在20世纪80年代，就已经有学者注意到研究矿石在溜井储矿段内的运移规律是研究磨损问题、优化储矿段结构参数、解决储矿段变形破坏问题的关键[7]. 郭宝昆和张福珍[8]根据矿岩在溜井中的移动规律将储矿段划分成了4个区域，并据此分析了不同区域下的溜井堵塞、磨损情况；谭志恢[9]称之为“分区理论”，认为储矿段矿岩移动主要受内崩落角影响，并首次引用椭球体放矿理论描述了矿岩整体的运动过程；近年来，王其飞[10]再次引用椭球体理论比较详细地将储矿段划分区域，定性分析了不同区域下矿岩的移动规律；刘艳章等[6]在此基础上，结合储矿段结构计算了各区域的高度分布. 相关研究工作持续了40多年，但由于缺乏能够预测矿岩运移过程中的轨迹、速度变化的相关理论或数学模型，目前仍仅能宏观地描述储矿段内矿岩运移特点. 主要原因是现有理论定量分析储矿段井壁边界对矿岩运移状态的影响较为困难，同时储矿段矿岩运移过程中力学机制复杂，相关研究至今没有建立起系统的矿岩运移方面的理论模型[11].若能引用合适的理论揭示储矿段矿岩运移特征，建立起矿岩位移、速度、放矿量和溜井结构参数等之间的关系，预测矿岩运移过程中的轨迹和速度分布特征，则能为深入分析矿岩流动性[12−13]、储矿段堵塞、井壁损伤等问题提供理论依据.

为深入探究溜井储矿段内矿岩运移特征和揭示其运移规律，本文以放矿漏斗中心线与溜井中心线重合型的溜井结构为研究对象，根据筒仓卸载过程中颗粒运动特点和流体力学中流动单元运动特点，建立储矿段矿岩运移网络，将Beverloo经验公式、流动网络等引用到储矿段矿岩运移特征的研究中，构建预测矿岩运移轨迹、速度的数学模型，为深入研究储矿段堵塞和井壁损伤等问题提供理论依据.

1 储矿 段运移 特征 三维预 测模 型的理 论基础

目前，对储矿段运移规律研究的理论基础仅有椭球体放矿理论. 但建立该理论的实验基础是无边界条件下放矿，不考虑边界条件对矿岩散体运动的影响[14]，而储矿段放矿过程中边界对矿岩的作用效果非常明显. 矿岩散体在运动过程中不仅受重力、内摩擦力，还受到井壁侧应力的作用[15].溜井储矿段结构参数的改变会导致侧应力的大小、方向发生变化，进而影响放矿过程中矿岩的运动速度和方向.

目前，研究固定边界条件下物质单元运动的理论主要有颗粒流动力学理论和流体力学. 一方面，出口在底部的筒仓颗粒卸载过程是颗粒流动力学研究的典型对象之一，而溜井储矿段的放矿过程与其极为相似，颗粒流动力学理论对于研究储矿段放矿过程具有其可应用性. 另一方面，相比于颗粒流、放矿学等理论，流体力学中涉及流体流动的理论体系更完整、相关计算方法也更系统、具体[16]. 储矿段矿岩运移主要受边界的“限制、阻碍”作用，受摩擦作用影响较小[17]. 与直流管中理想流体的边界作用[16]具有相似性.

由于矿岩在溜矿段运动过程中的力学机制研究仍存在缺陷，因此，在应用颗粒流动力学理论和流体力学建立模型时，以结构条件相似、矿岩粒径相近为基础，尽量规避复杂的力学问题分析，简化计算过程.

1.1 颗粒流动力学中的筒仓卸载问题

筒仓颗粒卸载方面的研究偏重于探究颗粒接触的力学机制和仓壁侧压力分布等问题，但由于力学作用过程复杂，许多机理至今尚未明确[18]，其中包括颗粒运动速度、轨迹的计算问题. 有学者从不同角度建立了颗粒速度计算模型[19]，但局限于二维空间而没有得到广泛应用. 目前，仅能够根据被广泛认可、使用的筒仓卸载方面的理论或研究，推测颗粒的大致运移迹线、放出口尺寸与颗粒流量之间的关系.

1.1.1 筒仓卸载过程中颗粒运移特征

在与储矿段结构参数等相似的筒仓重力卸载研究中，颗粒群在筒仓内的运动流型分为整体流和中心流[19]. 整体流常发生于内壁光滑、放出口倾角较大、内储颗粒间的黏结力较小的筒仓中，颗粒流动通道与筒仓壁一致. 中心流常发生于壁面粗糙、放出口倾角较小或平底的筒仓中，尤其是内储颗粒粒度较小或颗粒间黏结力较大的筒仓内. 中心流流动过程中，筒仓放出口附近存在小范围区域内颗粒不发生运动，该区域内的颗粒群形成一种类似漏斗的边界，减小了颗粒流动通道面积，Brown称之为“空环效应”[20]. 卸载过程中是否形成“空环效应”是评判筒仓内卸料流型的主要标准之一，筒仓放矿口半锥角、颗粒休止角（安息角）是影响“空环效应”产生与否的主要因素.

筒仓卸载方面的研究中虽然没有明确颗粒的流动迹线，但相关文献的实验结果[21]中发现，远离放出口处的颗粒呈直线匀速运动，方向铅垂向下.接近放出口处时，颗粒的运动方向会发生改变（中心线上颗粒仍铅垂向下），慢慢指向放出口；距离放出口越近，颗粒运移轨迹越接近直线，如图1.

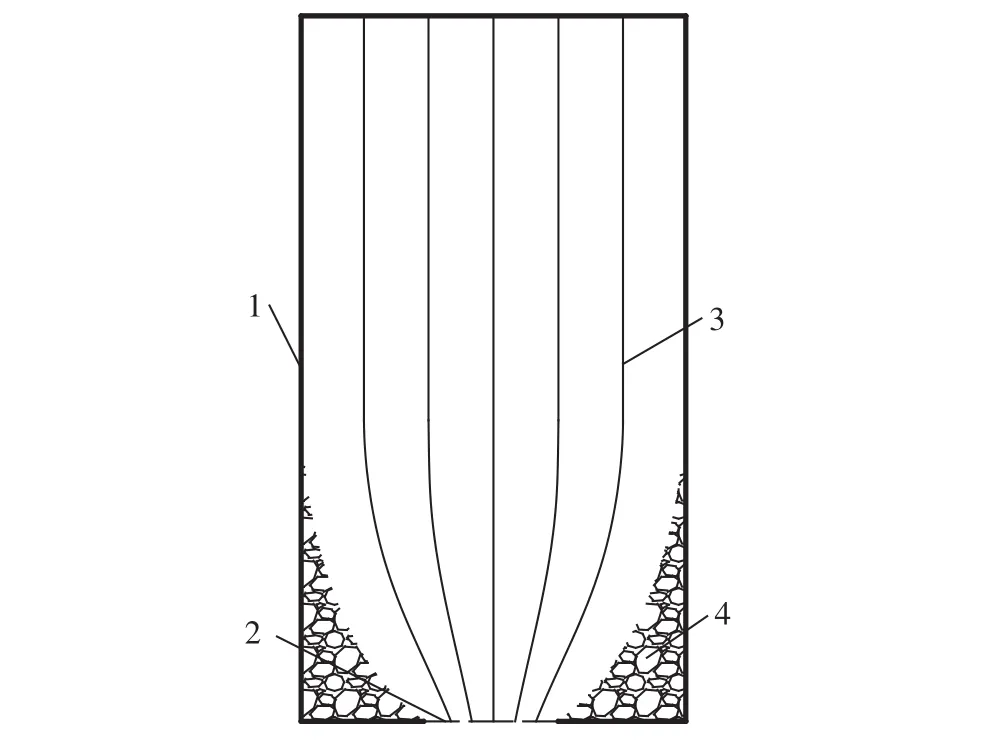
图1 筒仓卸载过程中颗粒运动迹线（1—筒仓边界；2—放出口；3—颗粒运动迹线；4—卸料死区）Fig.1 Particle movement trace during the silo unloading (1—the boundary of the silo; 2—ore draw hole; 3—particle movement trajectory;4—discharge dead zone)

1.1.2 Beverloo经验公式

Beverloo经验公式是颗粒流流量计算常用的基本理论公式之一[22]，大量研究证明了该公式的精确性和可靠性[23−24]，经过多年发展，该公式表达式为：

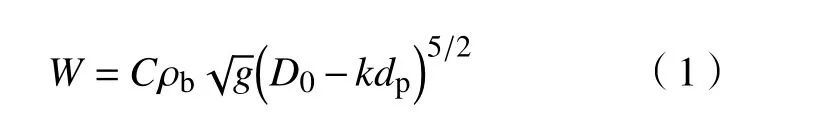
式中：W为单位时间内颗粒通过放出口的质量，kg·s−1；C 为量纲为一的常数，与筒仓结构有关，一般在 0.5到 0.7之间；ρb为颗粒床层堆积密度，kg∙m−3；g 为重力加速度，m·s−2；D0为筒仓出口直径，m；k为与颗粒形状有关的量纲为一的常数，一般在1.2和3之间；dp为颗粒粒径，m.

Beverloo经验公式表明，在筒仓结构一定的条件下，单位时间穿过筒仓内任意截面（该截面与矿岩运移的速度方向垂直）的颗粒质量是一定的，且与同一时间内通过放出口的颗粒质量相等. 式（1）也可以改写为面积与流量的关系式：其中S为放矿口处面积. 由于该公式是建立在颗粒连续运动条件下的，因此也适用于筒仓内部颗粒流动. 基于Beverloo经验公式的内涵，则能够建立颗粒位移、速度与流量等之间的关系.

1.2 流体力学中的理想流体问题

1.2.1 直流管下理想流体流动单元流动特点

理想流体流动过程中，容器边界主要起着限制流体流动范围、改变流体流动方向的作用. 因此，当直流管边界不变时，同一平面上的流体流动的单位速度相等且流动方向平行于管道中心；当直流管断面缩小时，流动单元向放出口运动，其速度随流动通道的缩小而增加[16]，如图2.

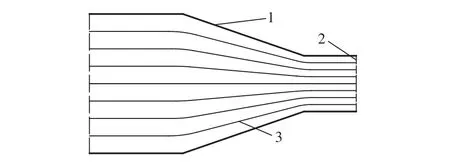
图2 直流管中理想流体流动特征（1—直流管边界; 2—放出口;3—流动单元运动迹线）Fig.2 Ideal fluid flow characteristics in a straight pipe (1—boundary of straight pipe; 2—ore draw hole; 3—movement trajectory of flow unit)

1.2.2 流动网络

流动网络反映了理想流体中流动单元的流动特点，是国内外分析理想流体流动过程的常用方法之一[16]，理想流体的二维流动网络如图3.

图3 流动网络（1—边界；2—流线；3—等位线）Fig.3 Flow network (1 —boundary; 2 —streamline; 3 —equipotential line)

二维流动网络由流线和等位线组成. 流线代表了理想流体内部流动单元的运移迹线，等位线与流线垂直，同一等位线上流动单元的流速相等.而三维流动网络中，通过同一点有无数条等位线组成唯一的等位面. 等位线和等位面的分布特征是建立三维流函数的基础.

1.2.3 流量与截面面积的关系

流体力学中，单位时间内流过任何截面的流体体积称为流量，在理想流体中通常指的是体积量. 体积流量的大小等于平均流速乘以与速度垂直的等位面面积[16]. 因此在给定的流动网络内，单位时间内穿过任意等位面的流量为一定值.

1.3 物质单元运动的相似性问题

根据颗粒流动力学和流体力学相关研究发现，在一定边界条件下，物质单元的运动状态是相似的. 而筒仓卸载过程的颗粒运动特征与直流管中理想流体流动特征具有一定的相似性，其边界条件和物质单元运动的相似性表现为：在放矿漏斗中心线与容器中心线重合、不考虑容器边界摩擦作用等条件下，固定边界中物质单元的运动特征具有相似性. 在远离放出口范围内或物质流动通道不变时，物质单元作匀速直线运动，各单元间相对速度为零；在放出口附近或当物质流动通道缩小时，物质单元运动迹线发生变化，运动方向逐渐指向放出口. 此外，在物质单元运动过程中，单位时间内通过与物质单元运动速度垂直的截面的物质总质量是一定值，与该截面面积、物质单元运动速度有关.

1.4 矿岩运移轨迹和速度预测模型理论基础

1.4.1 矿岩运移规律

根据一定条件下物质单元运动状态的相似性，结合放矿漏斗中心线与溜井中心线重合条件下溜井储矿段结构的特点，将储矿段分为矿岩匀速运动区（以下简称匀速区）、矿岩变速运动区（以下简称变速区）、平衡区. 若放矿口边墙与水平面的夹角（即放矿口倾角）为α，由于α的不同，矿岩运动特征会出现无平衡区和有平衡区两种情况，如图4.

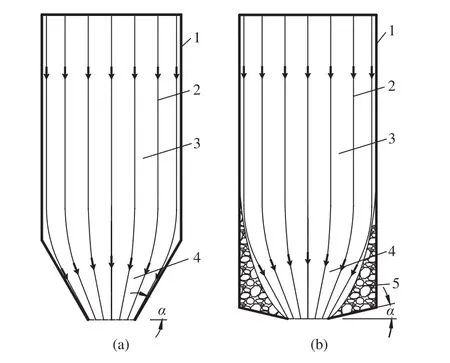
图4 溜井储矿段矿岩运移规律（1—溜井储矿段边界；2—流线;3—矿岩匀速运动区；4—矿岩变速运动区；5—平衡区）. （a）无平衡区时；（b）有平衡区时Fig.4 Ore-rock migration law in the ore-storage section of orepass(1—boundary of ore-storage section in orepass; 2—streamline; 3—uniform velocity area of ore-rock motion; 4—variable speed area of ore-rock motion; 5 —equilibrium area): (a) nonequilibrium area; (b) equilibrium area

当放矿口倾角较大时，放矿口附近没有矿岩“滞留”，矿岩呈“整体流”下移. 在这种情形下，根据矿岩流速的变化特征，储矿段可划分为匀速区和变速区两部分，即储矿段筒仓结构范围为匀速区，放矿口上部漏斗结构范围为变速区，如图4（a）；当放矿口倾角较小或平底放矿时，放矿口上部一段范围内存在矿岩流动“死区”，导致“空环效应”，减小了矿岩流动通道面积. 该区域内矿岩堆积，不发生位移，可称之为平衡区. 以平衡区上标高为界，标高以上为匀速区，标高以下为变速区，如图 4（b）.

矿岩在不同区域中的运移过程呈现出如下特征：

（1）匀速区内矿岩整体下移，矿岩块作直线下向运动；

（2）平衡区内矿岩不发生运动，形成类似漏斗型的矿岩滑动边界，减小了矿岩流动通道面积；

（3）变速区内矿岩块受边界影响，矿岩开始向放矿口移动，运动方向由铅直向下慢慢指向放矿口，作曲线运动（中心线上矿岩作直线运动），越接近放矿口，矿岩轨迹越接近直线.

1.4.2 储矿段矿岩运移网络

参考流体力学三维流函数计算方法，将矿岩的滑动边界面视为平面，变速区内矿岩运移迹线视为直线，同时，假设系统存在一等位面作为匀速区和变速区的分界面，当矿岩位于该等位面以上时，其运动特征符合匀速区运移特征；当矿岩位于该等位面以下时，符合变速区运移特征. 根据储矿段内矿岩运移特点和理想流体流动网络绘制方法，建立储矿段矿岩运移网络，如图5.

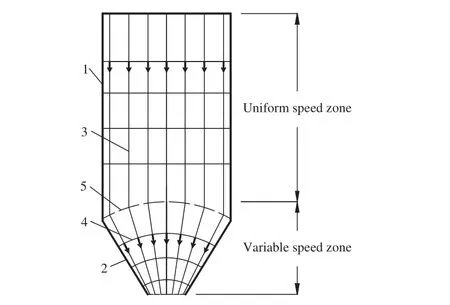
图5 储矿段矿岩运移网络（1—边界；2—滑动边界；3—流线；4—等位面；5—分界等位面）Fig.5 Ore-rock migration network in ore storage section (1—boundary;2—sliding boundary; 3—streamline; 4—equipotential surface; 5—demarcation equipotential surface)

匀速区内矿岩流线为铅垂向下的直线，等位面为储矿段匀速区范围的横截面；变速区内矿岩流线指向放矿口下放矿漏斗中心线上一点，等位面为放矿漏斗横截面截取的球面，其球心在放矿口下放矿漏斗中心线上. 流线和等位面的分布特征反映了矿岩位移、速度与边界、放矿量的几何关系.

2 溜井储矿段矿岩运移预测模型基本假设

针对放矿漏斗中心线与溜井中心线重合的溜井，为建立储矿段矿岩运移预测模型，定量分析矿岩运移轨迹和速度，预测不同初始位置下矿岩颗粒运移方向、位移及速度变化，根据矿岩运移规律和图5，作如下基本假设：

（1）储矿段放矿过程中矿岩的运动过程是连续的；

（2）矿岩运动规律符合储矿段矿岩运移网络分布特征；

（3）不考虑井壁与矿岩块的摩擦作用.

2.1 矿岩位移及运移轨迹方程

2.1.1 匀速区内矿岩位移及运移轨迹方程

匀速区内，矿岩散体整体全断面匀速下移，如图6. 设匀速区内某一矿岩块初始位置A0，坐标为(x0，y0，z0)，经过时间 t后，该矿岩块到达 A1点位置，坐标为(x1，y1，z1). 由于矿岩作下向直线运动，仅z值发生变化，矿岩下降高度等于矿岩在t时间内的位移量，建立关系式如下：

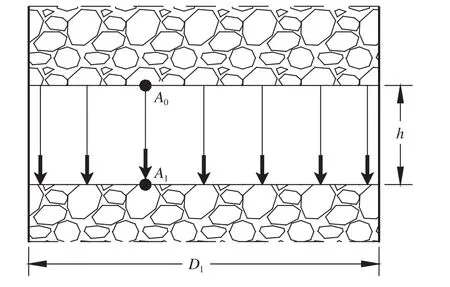
图6 匀速区内矿岩运移过程分析Fig.6 Analysis of ore-rock moving in the uniform velocity zone

在匀速区内，矿岩整体下移，矿岩放出量与穿过A0点的横截面（等位面）的矿岩质量相等. 由于穿过该截面的矿岩就是在A0点和A1点各自所在等位面之间的矿岩，可建立关系式如下：

式中：W1为t时间内放出矿岩质量，kg；W0为单位时间内矿岩通过放出口的质量，kg·s−1；W2为 t时间内穿过A0点的横截面（等位面）的矿岩质量，kg；D1为储矿段的断面直径，m；ρP为储矿段的矿岩密度，kg∙m−3.

式中：ρb为矿岩床层堆积密度，kg∙m−3；；D0为放矿口直径，m；dp为矿岩颗粒粒径，m.

结合式（2），放矿t时间后矿岩位置坐标（x1，y1，z1）为：

式（5）即为矿岩在匀速区的运移轨迹预测模型.

2.1.2 变速区内矿岩位移及运移轨迹方程

变速区内，矿岩块向放矿口运移，将其运动轨迹简化为直线，运动方向指向放矿口下放矿漏斗中心延长线上一点O，如图7. 设该区内某一矿岩块初始位置为 B0（x2，y2，z2），经过时间 t后，该矿岩块到达 B1点（x3，y3，z3）. 根据图 7可知，B0和 B1即在半径为R0、R1的球面上，又在穿过原点的一条直线上，矿岩块在t时间内的位移值为R0与R1之差，方向指向O点，可建立关系式如下：

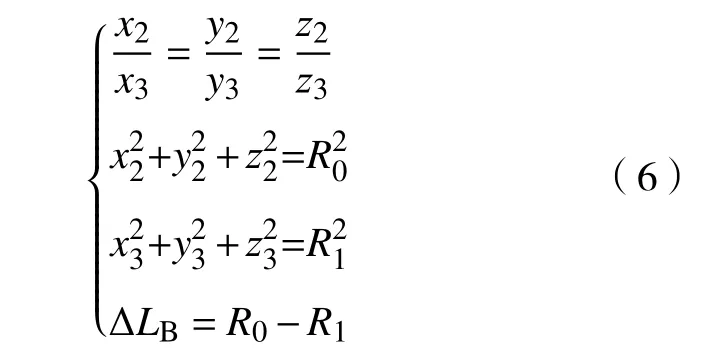
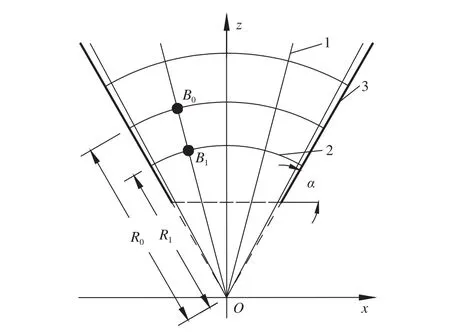
图7 变速区内矿岩运移过程分析（1—流线；2—等位面；3—滑动边界）Fig.7 Migration process analysis of ore-rock in variable speed zone(1—streamline; 2—equipotential surface; 3—sliding boundary)

式中：R0为B0点所在等位面的半径，m；R1为B1点所在等位面的半径，m；Δ LB为矿岩在t时间内的位移，m.

根据储矿段矿岩运移特点和图7，在变速区内矿岩放出量与穿过B0点的横截面（等位面）的矿岩质量相等，由于矿岩整体下移，穿过该截面的矿岩即为在B0点所在等位面和B1点所在等位面之间的矿岩，矿岩体积变化量为半径R0、R1的球顶椎体的体积差. 建立关系式如下：

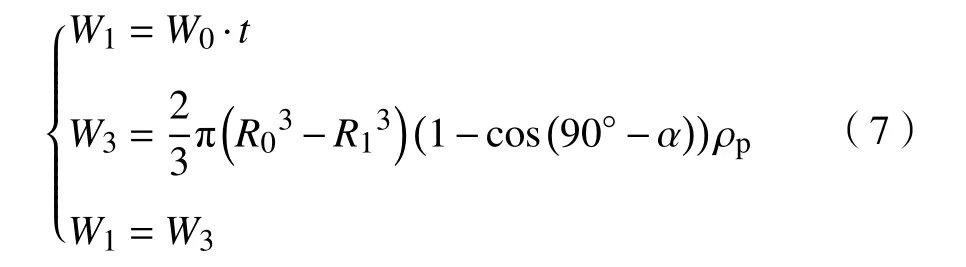
式中：W3为穿过B0点和B1点的横截面（等位面）之间的矿岩质量，kg；α为矿岩滑动边界倾角，（°）.

根据式（1）、（6）和（7），得到放矿 t时间后矿岩的位置坐标（x3、y3、z3）为：

式（8）即为矿岩在变速区的运移轨迹预测模型.

根据放矿前后的矿岩块位置坐标，可求得矿岩块从B0运移到B1位置的位移量关系式如下：

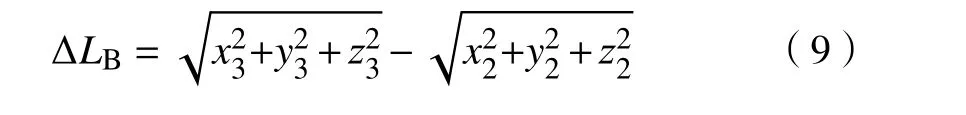
2.2 矿岩运移速度方程

2.2.1 匀速区内矿岩运移速度方程

根据矿岩在匀速区内运移过程分析（如图6），匀速区内矿岩作匀速直线运动. 因此，矿岩在经过时间t后下降高度与矿岩速度的关系如下：

式中：vA为矿岩在 A0点的速度，m∙s−1.

结合式（1）、（2）、（3）和（10），可得到矿岩在匀速区内运移速度方程如下：

2.2.2 变速区内矿岩运移速度方程

由于矿岩在变速区内的运动视为变速直线运动，因此不能通过矿岩的位移量计算其速度. 根据“单位时间内穿过任意截面（与速度垂直）的矿岩质量为定值”这一特点，∆t时刻内放出矿岩量与同时刻内穿过B点所在等位面的矿岩质量相等，根据稳定质量流动量定理[25]，可建立以下方程：

式中：dm/dt为质量流，kg∙s−1；ρ 为流体单元密度，kg∙m−3；v为流体单元速度，m∙s−1；s为流体单元所在截面面积，m2；Q为流体体积变化量，m3.

如图8所示，过B0点的等位面为圆心在O点、半径为 R0的球冠表面. 结合式（6）和式（12）可建立关系式如下：

图8 储矿区内矿岩运移过程分析（1—流线；2—等位面；3—滑动边界）Fig.8 Analysis on ore-rock moving in the storage section in ore pass(1—streamline; 2—equipotential surface; 3—sliding boundary)

式中：Q0为放出的矿岩的体积，m3；vB为矿岩在B0点的速度，m∙s−1；sB为 B0点所在等位面的面积，m2；hB为等位面形成的球冠高度，m.

整理式（13）可得矿岩在变速区内B0点的速度方程为：

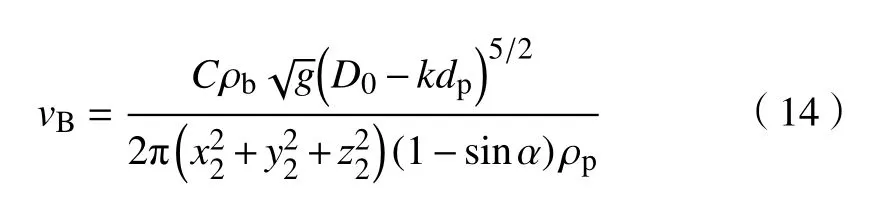
式中：vB为矿岩在 B0点的速度，m∙s−1.

2.3 矿岩的速度分区及特征

由图5可知，矿岩在从匀速区向变速区运动过程中，存在一速度分界等位面，在该速度分界面上，矿岩块的运移速度满足以下特征：

设该等位面上一点 D 坐标为（xD，yD，zD），整理可得：

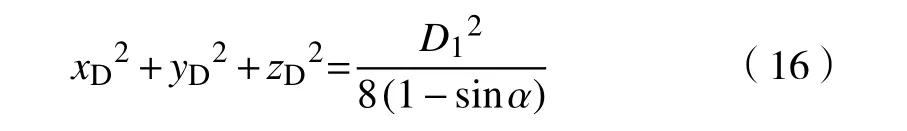
因此，根据式（16），可得出矿岩在匀速区和变速区运移的条件方程如下：

由式（17）可知，分界等位面为一球面，球面半径与储矿段的断面直径、放矿口倾角有关.

3 讨论

了解并掌握矿岩散体在溜井储矿段内的运动规律是揭示溜井堵塞以及井壁损伤问题发生机理的研究基础. 但是，矿山实际生产过程中储矿段内矿岩运移速度、轨迹是无法通过常规手段测得的.溜井储矿段矿岩运移预测模型提供了一个依据溜井结构参数、矿岩粒径、放矿时间等在矿山生产现场中可测指标，来预测矿岩运移速度、轨迹的计算方法. 采用该模型，可以进一步分析储矿段矿岩运移速度场、位移场等，探究矿岩块组合成拱问题；在研究溜井井壁损伤问题方面，由于井壁摩擦作用会降低矿岩运移速度，造成矿岩动能损失. 损失的能量被井壁材料吸收，引起塑性变形，可采用该模型，进一步分析有摩擦和无摩擦作用下与井壁接触的矿岩速度及方向变化，计算井壁相切方向上矿岩运动过程中的动能损失量，结合井壁应力分布特征，可探究井壁损伤变形特征.

4 结论

（1）根据筒仓物料卸载过程和直流管下理想流体流动过程中质量单元运动特点，研究了放矿漏斗中心线与溜井中心线重合的溜井结构条件下，溜井储矿段内矿岩散体运移规律，将储矿段矿岩运移分为匀速区、变速区、平衡区. 匀速区内矿岩作直线向下运动，速度不变；变速区内矿岩作曲线运动，速度随位置而变化；平衡区内，矿岩不发生位移.

（2）引入流动网络概念、Beverloo经验公式、稳定质量流动量定理等，建立了溜井储矿段的矿岩散体运移规律预测模型. 该模型在已知储矿段结构参数、矿岩粒度、位置坐标等条件下，能够计算矿岩在储矿段内任意一点的速度以及放矿t时间后矿岩位移量及其位置坐标，定量分析矿岩块运移过程.

（3）根据所建立的储矿段矿岩运动预测模型可知，在储矿段连续放矿过程中，单位时间内放出矿岩量和通过与速度垂直的截面的矿岩质量为一定值，该值与筒仓结构、矿岩层密度、放矿口直径、重力加速度、矿岩粒度和形状有关，与储矿段高度无关.

（4）建立的矿岩位移、运移轨迹和速度方程，适用于放矿漏斗中心线与溜井中心线重合条件下，储矿段内矿岩散体运移轨迹及速度的预测. 当放矿漏斗中心线与溜井中心线不重合时，应用这些方程会存在较大的差异.