指向关键能力发展的高三数学第二轮复习教学*——以求“二面角”为例

吕增锋|浙江省象山县第二中学

高三数学第二轮复习是学生在备战高考中必须经历的重要阶段之一，它是在第一轮复习对高中数学基础知识回顾与梳理的基础上，全面开展的专题性复习.与第一轮复习相比，第二轮复习有两个特色：关注重点、难点和易混淆点，重在对知识点进行深化和细化；注重理论与实践的结合，对已掌握的知识进行反复训练和巩固，重在提高学生的学习状态和应对考试的信心.第二轮复习的目的是进一步完善学生的知识体系与结构，不断总结破解数学问题的规律和技巧方法，从而全面提升学生的数学关键能力.

一、数学关键能力的内涵及其在数学解题中的作用

数学关键能力是将数学的核心知识内容与数学思想方法形成纵向的联结，并且在横向层次上结合一般数学能力的一种综合能力.从心理学角度分析，数学关键能力指的是学生通过数学活动的展开，在所掌握的数学知识的铺垫下，运用数学思想、数学方法、数学活动经验解决数学问题的心理特征.《中国高考评价体系》从考试评价的视角把关键能力概括为三个能力群，即知识获取能力群、实践操作能力群和思维认知能力群。它可以进一步具化为：逻辑思维能力、抽象思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力［1］.

数学关键能力在数学解题中扮演着非常重要的角色.解题的第一步是分析问题，这就要求学生具备较强的逻辑思维能力，能够把复杂的问题拆分成简单的问题，能够快速建立条件与结论之间的联系，从而为问题的正式解决做好准备.在解题过程中，学生要能够根据已知信息和问题要求，从多个方面思考分析，并及时调整自己的解题思路，合理选择解题方法.同时，解题需要进行大量的计算，学生不仅需要具备运算求解能力，而且必须快速、准确，并能够判断计算结果的正确性.因此，数学关键能力对于能否成功解题至关重要.

二、指向数学关键能力发展的第二轮复习的思路

第二轮复习教学须借助多方面的教学资源和技术手段，帮助学生加强数学关键能力.下面，笔者以“二面角”为例，谈谈具体的做法.

（一）在诊断中明确学生数学关键能力的短板

数学学习应做到有的放矢，要实现这一目的，关键是教师能充分掌握学生的“前见”，即学生在新课学习之前已经获得的知识、技能和经验.这些前期获取的知识和经验可以对学生后续的学习产生重要的影响和作用［2］.数学第二轮复习也应如此，首先应该对学生的“前见”进行全面分析，了解学生对数学关键能力的掌握情况.诊断学生数学关键能力的方法和手段，一般有测验、观察记录、学生自我评价、同伴评价等几种.

笔者先用2021 与2022 年新高考全国I 卷与II卷中“二面角”的真题对学生进行了检测，并对测验的结果进行统计，发现全班45人中，35人选择用向量法，正确率为43%，10人选择用几何法，正确率为30%.这表明，多数学生选择用向量法，并且做对的情况要好于用几何法.接着，笔者从数学关键能力的视角对学生主要错误的原因进行分析（如表1所示）.

不难发现，在求二面角的过程中，学生在逻辑思维能力、空间想象能力、创新能力的表现上存在较大不足，这些不足需要通过后续的学习加以提升，同时这也为第二轮复习明确了方向与任务.

（二）在展示中让学生认识到数学关键能力的不足

学生虽然知道自己解题出错了，但对错误是怎么发生的、有什么共同的特征、涉及哪些数学关键能力等一系列问题，还是一头雾水.这就需要从加强学生数学自我认知入手.数学自我认知是数学学习的重要因素之一，对学生学习积极性、学习效果等都有巨大的影响.

展示典型的错误与优秀解法是学生开展数学自我认知的最佳途径.笔者先挑选一些解法错误或答题不规范的案例，投影在屏幕上，采用学生互评的形式，让学生找错误、析错因、纠错法.通过深入地分析错误的原因和表现方式，学生可以更好地理解错误的本质，进而纠正错误.同时，这也有助于学生强化正确的解题思路，从而让错误成为学生发现问题和深入思考的催化剂.接着，笔者呈现优秀的解题案例，同样采用学生互评的方式，让学生找亮点、说感受、提建议，在帮助学生树立解题规范的同时，引发学生思维的碰撞与情感的共鸣.通过对比展示，学生能够领悟到优秀的数学解题所具备的三大特征，即“清晰的思路、简洁的过程、优化的算法”，而要做到这些，数学关键能力起到了决定性的作用.

（三）在关联中让学生的数学关键能力得到强化

将问题中的各个部分联系起来，从整体的角度来研究问题，可使学生在解决数学问题时具有更高的思维能力和处理能力，这就是整体关联思想.在数学解题中的具体做法是：既要考虑知识前后的关联性，又要分析数学思想方法之间的关联性，还要兼顾学生学习经验之间的关联性；然后在充分认识关联性的基础上，整合各种解题技巧，从而创造出更好的解题方案.在建立关联性的过程中，学生不仅能够更深刻地理解数学的本质和应用场景，而且可以形成更广泛、更深层的数学思维，从而进一步强化个人已有的数学关键能力.

例题：（2022年新高考全国I卷第19题）如图1，直三棱柱ABC-A1B1C1的体积为4，△A1BC的面积为

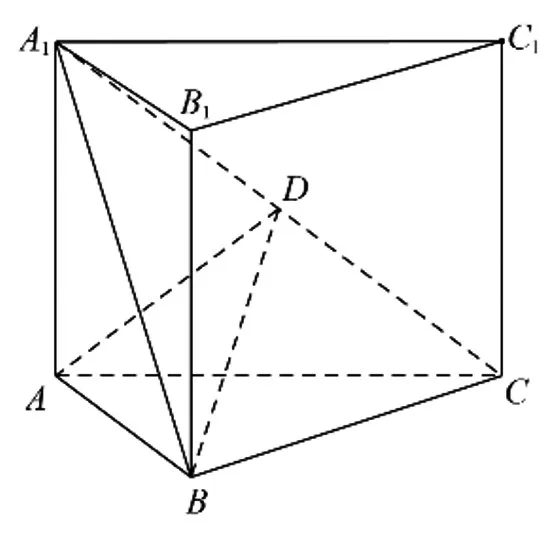
图1

（1）求A到平面A1BC的距离；

（2）设D 为A1C 的中点，AA1=AB，平面A1BC ⊥平面ABB1A1，求二面角A-BD-C 的正弦值．

对于上述“二面角”问题，学生想到以下一些方法.

定义法1：直接作二面角ABD-C 的平面角.易证 △ABD 与△CBD 全等，过A 点在面ABD 上作AF⊥BD，连接C、F，则∠AFC 就是二面角A-BD-C 的平面角，用余弦定理求出cos∠AFC.

定义法2：利用三垂线定理作出二面角A-BD-C 的平面角.过A 点在面AA1B 上作AE⊥A1B，垂足为E，易证AE⊥面A1BC；过E 点在面A1BC 上作EF⊥BD，垂足为F；连接A、F，由三垂线定理得AF⊥BD，则∠AFE就是二面角A-BD-C 的平面角的补角，在直角三角形AFE中求出sin∠AFE.

射影面积法：利用公式在“定义法2”中，可知△BDE 是△ABD 在面A1BC的射影，则其 中θ 与 二 面 角A-BD-C 平面角互补.

上述方法都是从几何法衍生出来的，当然，向量法也可以衍生出很多方法，例如，基底法、坐标法等.但单纯的方法罗列远不足以提升学生的解题水平，学生还需对这些方法进行关联性思考，比如，方法之间有什么联系，是如何想到的，不同的方法表现出怎样的优势等，由此激发学生的深度思考，进而对学生在求二面角中所表现出来的数学关键能力来一次大的梳理与强化.笔者通过让学生画思维导图的方式来实现这一目的，学生所画的思维导图进行整合后的成果如图2所示.

（四）在微专题教学中让学生的数学关键能力再生长

在数学第二轮复习中，微专题教学可以很好地弥补学生数学关键能力的短板.微专题指围绕重点和关键点设计的，利用具有紧密相关性的知识或方法形成的专项研究，或者结合学生的疑点和易错点整合的，能够在短时间内专门解决的问题集.通常把以微专题为载体的“小切口”教学称为微专题教学，与一般专题教学相比，它具有“因微而准、因微而细、因微而深”等优点［3］.通过前面的诊断，教师已经充分了解了学生数学关键能力的薄弱面，围绕薄弱面来设计微专题可以确保选题的精准.比如，针对“创新能力”的不足，笔者设计“借助多种视角求二面角为主题”的微专题，主要由“一道例题+一个变式+若干道练习”组成.

例题：如图3，平行六面体ABCDA1B1C1D1，棱长都为2，且∠C1CB=∠C1CD=∠BCD=600，求平面C1BD与平面BDD1B1所成角的余弦值.

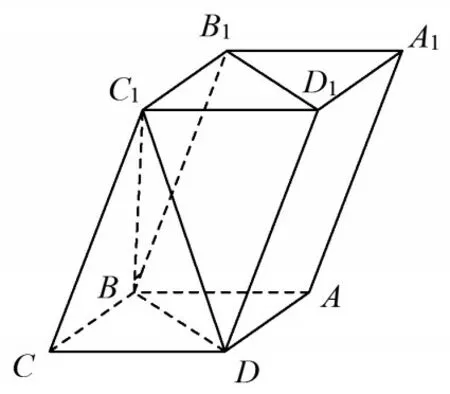
图3

相对于直棱柱，斜棱柱模型更适合作为发展学生空间想象能力的载体，因为斜棱柱往往没有现成的可以作为空间建系的垂直关系，这就需要学生对空间位置关系进行深入的观察与挖掘，由此可引发对解题思路的新思考.在教学过程中，除了常规的“直接作二面角的平面角”与“坐标法”外，学生还想到了“角的转化”，即把二面角的平面角进行等角转化，并利用“基底法”求出结果.

这道例题打开了求二面角的新视角，对学生而言，实现了从“直接求角”走向“间接求角”的跃迁，从而为运算的简化提供了新的可能.为了进一步强化这种求角的意识，笔者在原题基础上设计了变式.

变式：平行六面体ABCD-A1B1C1D1，CC1＝4，CD＝2，CB＝3，∠C1CB=30°,∠C1CD=45°，∠BCD=60°，求平面C1BD 与平面BDD1B1所成角的余弦值.

对于变式，解题思路不变，但运算量增加了，这有助于进一步发展学生运算求解的能力.最后，笔者设计对应的习题，让学生经历更多类型的“角的转化”，比如，把二面角的平面角转化为与之对应的余角、补角等，让学生的数学关键能力得到持续的拓展.

综上，高三数学第二轮复习一直面临着诸多问题，如：重视题型教学，忽视思维暴露；重视技巧方法，忽视数学思想；重视教学进度，忽视认知基础；过度练习，节奏错乱；被动性学习，机械训练.这主要是因为复习目标定位出现了偏差，没有把高三数学第二轮复习的目标指向发展学生的关键能力.也就是说，超越高三数学第二轮复习困境的路径，根本在于复习目标的转变，教师要以发展数学关键能力为导向，通过对复习内容的整合与重构，让复习教学处于辩证发展和持续优化之中.