一种新型1T2R并联机构的运动学及工作空间分析

邱冰,李小兵,石志新,贾超逸,罗玉峰

(南昌大学先进制造学院,江西 南昌 330031)

欠秩并联机器人机构具有结构紧凑简单、设计加工简便、控制简单等优点,是机构学研究领域的热门之一[1-3],在工业生产以及航空等其他领域具有广泛的应用前景[4-8]。

近年来,许多来自国内外的学者研究了三自由度并联机构机器人拓扑结构类型。1983年,1T2R型三自由度并联机构3-RPS首次由Hunt[9]提出。冯永平等[10]运用方位特征集理论对一平移二转动并联机构进行了型综合,给出了一平移二转动输出并联机构拓扑结构设计的一般步骤及其具体方法。张志良等[11]运用螺旋理论分析了一平移两转动机构及其位置。季青等[12]以一平移两转动机构为研究对象,分析其机构运动学和工作空间。沈惠平等[13]对单自由度一平移两转动并联运动振动筛进行了动力学分析,为多回路并联机构动力学参数优化提供了理论基础。谢冬福[14]等提出了一种并联腿六足农业机器人,对并联腿机构运动学和工作空间进行了深入研究。陈淼等[15]设计了一种3-RPS/SPS并联机构,通过建立其运动学模型和使用闭环矢量法,系统地分析了机构正逆运动学。

本文提出一种新型1T2R并联机构2-SPS/PRR。首先利用方位特征方程对该机构进行拓扑结构分析,得到其方位特征集。根据Yang和Sun提出的更具有一般性的自由度(degrees of freedom,DOF)公式,验证其DOF。利用封闭矢量法分析其运动学逆解,机构运动学正解通过多种群遗传算法得到,并与逆解相互印证,而后基于蒙特卡洛算法求解其工作空间,最后进行运动学仿真分析得到其运动变化曲线,为后续研究和设计该类型的机械构型提供参考依据。

1 并联机构结构分析

1.1 机构设计

2-SPS/PRR并联机构结构简图如图1所示,机构由3条支链构成,其中支链一的拓扑结构表示为SOC{-P11-R12R13-},支链二、三拓扑结构表示为SOC{-Si1-Pi2-Si3}(i=2,3)。

图1 2-SPS/PRR并联机构Fig.1 2-SPS/PRR parallel mechanism

1.2 并联机构拓扑分析

1.2.1 确定支路末端构件的POC集

2-SPS/PRR并联机构三维模型见图2所示。

图2 2-SPS/PRR并联机构三维模型Fig.2 3D model of 2-SPS/PRR parallel mechanism

支路1的方位特征集(POC集):

取R12副与R13副的两轴线交点为基点,支路SOC{-P11-R12R13-}末端构件的POC集为

(1)

式中:t为独立移动元素;r为独立转动元素;P为移动副;R为转动副;||表示平行;◇表示平面。

支路2、3的方位特征集(POC集):

支路SOC{-Si1-Pi2-Si3}(i=2,3)末端构件的POC集为

(2)

1.2.2 建立并联机构方位特征方程

根据并联机构方位特征集的运算规则,将三支路的末端机构的方位特征集带入并联机构方位特征方程中,得到

(3)

1.2.3 检验机构自由度

由于机构的DOF对POC集的运算产生约束,因此需要对并联机构的自由度进行检验。

通过分析组成该并联机构的3条支路的拓扑结构,以及3条支路在动、静平台之间的装配关系,根据Yang和Sun提出的更具有一般性的DOF公式:

(4)

式中:F为机构DOF;fi为第i个运动副的自由度的数目;m为运动副的数目;v为独立回路的数目;ξLj为第j个独立回路的独立位移方程数;Mbi为第i条支路末端POC集;dim.{M}表示方位特征集的维数。

1) 第1个独立回路的独立位移方程数ξL1的计算。

第1个独立回路由第一、二条支路组成,由式(4),ξL1为

(5)

第一、二条支路组成的子并联机构自由度为

(6)

第一、二条支路组成的子并联机构的动平台的POC集为

(7)

2)第二个独立回路的独立位移方程数ξL2的计算。

考虑到P11、P21与P31副为空间任意交叉,则

ξL2=dim.{Mpa(1-2)∪Mb3}=

(8)

第一、二、三条支路的子并联机构的DOF为

(9)

所以,机构的自由度为3满足设计要求。

2 2-SPS/PRR并联机构正逆解分析

2.1 并联机构的描述及动坐标系、静坐标系的建立

如图3所示,2-SPS/PRR并联机构由静平台、动平台和位于它们之间的3条支路组成。3条支路中间均为移动副,且以3个移动副作为机构的驱动副,通过驱动装置推动移动副发生相对位移,使得3条杆的杆长发生变化,从而改变动平台的空间位置和空间姿态。设定该动、静平台均为正三角形,动平台B1B2B33个点均匀分布在半径为r的圆周上,静平台A1A2A33个点匀分布在半径为R的圆周上。

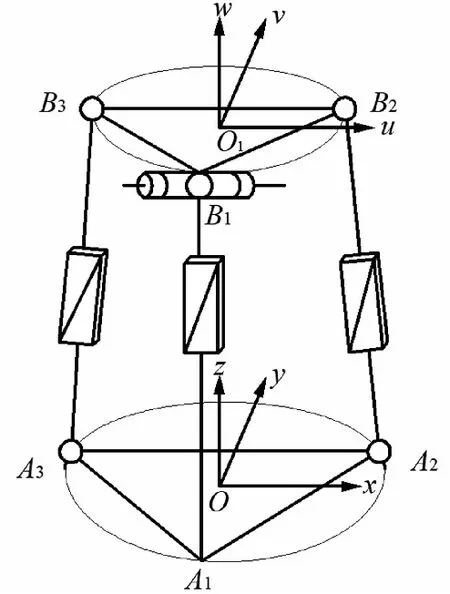
图3 2-SPS/PRR并联机构坐标系Fig.3 Coordinate system of 2-SPS/PRR parallel mechanism

分别在动平台和静平台所处圆周的圆心处建立动坐标系{O1uvw}和静坐标系{Oxyz}。静平台x轴平行于A2A3,y轴垂直于A2A3,z轴由右手螺旋定则可知垂直于静平台。动平台u轴平行于B2B3,v轴垂直于B2B3,由根据右手螺旋定则可确定w轴的方向为垂直于动平台。

与传统并联机构相比,此并联机构各支链位置分布方式一致且对称性好,3条支链均布置一个驱动副关节,支链结构简单且相似。因此,该机构具有复杂度低、稳定性好、不存在伴随运动和易于控制的特点。

2.2 机构逆解分析

并联机构逆解分析是:通过已知的末端执行器的空间位置和空间姿态,求解各个关节输入量的取值。

对于此并联机构的逆运动学分析是:给定动平台的空间位置参数和姿态转角参数,即动平台沿z轴的位移d和关于x轴旋转的角度γ及关于y轴旋转的角度β,求出对应3条支链的杆长长度L1、L2、L3。

常用的逆运动学求解方法一般有2大类:

封闭解和数值解,其中封闭解通过不同方法将约束方程中的未知数消去,得到解析表达式后再解得方程的所有解。而数值法一般不能求得所有解,因此不适合进行理论上的研究,并且数值解法比封闭解法更加耗时且复杂。因此本文采用封闭矢量法求解此并联机构运动学逆解。

根据在动平台位置处建立的动坐标系{O1uvw},确定3条支链与动平台连接处各点的齐次坐标如下:

(10)

根据在静平台位置处建立的静坐标系{Oxyz},确定3条支链与静平台连接处各点的齐次坐标如下:

(11)

由2-SPS/PRR并联机构的运动特征可知:

动平台位移与各个支链末端位移相等,动平台存在2个方向的转动。因此,根据动平台与静平台的位置关系,动坐标系{O1uvw}相对于定坐标系{Oxyz}的齐次变换矩阵为:

(12)

式中:trans为平移矢量;Rot为旋转矢量;sβ、sγ分别表示sinβ、sinγ;cβ、cγ分别表示cosβ、cosγ,下同。

(13)

通过机构矢量关系得到各个驱动副的杆长计算公式分别为:

(14)

并联结构各支链均以移动副作为机构的驱动副,因此只需给定动平台的位置和姿态参数,即给定β、γ、d,逆解的求解即可式(14)求得。通过Matlab求得以下5组算例下对应的杆长l1、l2、l3的尺寸,见表1。

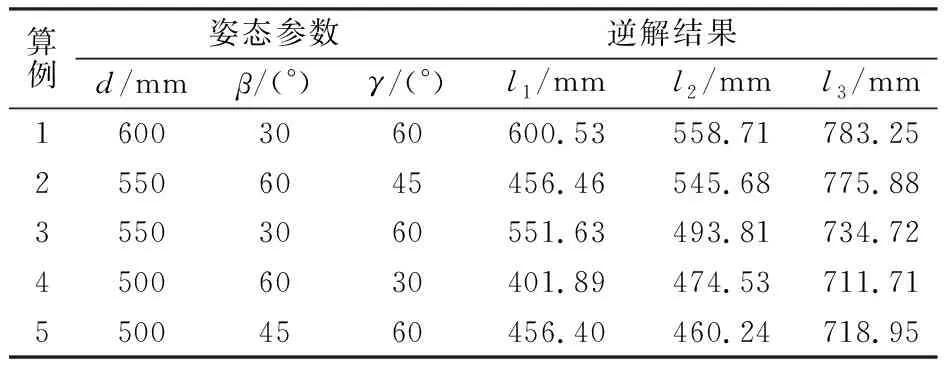
表1 逆解算例Tab.1 Example of inverse solution

2.3 基于多种群遗传算法的正解分析

并联机构由于自身结构相对复杂,其位置的正解具有很大的难度。本文运用多种群遗传算法对并联机构进行正运动学分析,多种群遗传算法通过使用群体搜索技术,将一组问题的解放入各个种群中,并对各个种群实施进行一系列的选择、交叉和变异等遗传操作,且各个种群的进化方向不同,使得搜索能力得到大幅增强,并生成新一代的种群,各个不同的种群之间通过移民算子进行相互联系,即分别把每个种群的最优个体分别引进到其他种群中,通过多个种群共同进化而取得最优解。与传统遗传算法相比,多种群遗传算法能有效避免早熟问题,且提高了全局搜索能力,从而减少迭代次数和时间,提高了求解效率。

以并联机构的正解为最优搜索目标,引入适应度函数F,建立并联机构正运动学的数学求解模型。图4为多种群遗传算法运算流程图。

图4 多种群遗传算法流程图Fig.4 Flow chart of multi population genetic algorithm

1)确定优化目标函数。

建立关于z、β、γ的目标函数如下:

(15)

2)适应度函数。

适应度函数根据求解问题本身的要求而定,因此本算例的适应度函数构造是将目标函数直接映射成适应度函数,令F=|f1|+|f2|+|f3|为个体适应度函数,当F<10-7时,终止迭代,其中多种群遗传算法参数见表2。

说起天窗，我们并不陌生。那些最初被我们称为“囱”“通孔”的口子，就是最早期的“天窗”雏形。1941年，世界上第一座真正意义上的天窗在丹麦出现。在人们对建筑光环境的迫切需求下，建筑天窗应运而生，并深得许多设计师的青睐，开始出现在一些公共建筑及住宅项目中。进入21世纪，随着科学技术的进步，天窗的设计与功能也变得越来越丰富，甚至一度成为现代建筑设计的潮流。既是窗户也是天花，天窗的混合性使其能够成为建筑空间中的关键元素。不得不说，利用天窗的形状和角度加以灵活地布置，任何空间皆可变得独特而美观，仅仅是和天空近距离的接触，就能改变空间给人的第一印象，这大概就是天窗的魅力所在。

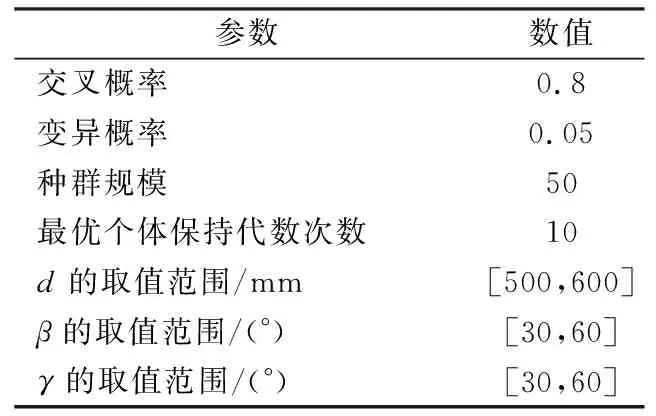
表2 遗传算法参数Tab.2 Parameters of genetic algorithm

由位置正解的计算结果表3可知,在给定杆长参数下,通过多种群遗传算法可以得到动平台位置和姿态的数值解。

表3 正解计算结果Tab.3 Calculation results of positive solution

由图5可知,5组算例的适应度曲线收敛速度均较快,当迭代次数为50次时,5组算例的适应度值均趋近为0。由此可知,多种群遗传算法可以有效且迅速地得到该并联机构的正解,同时也为此并联机构工作空间的求解问题提供理论基础。

进化代数图5 多种群遗传算法适应度曲线Fig.5 Fitness curve of multi population genetic algorithm

3 工作空间分析

并联机构的工作空间是指机构动平台上的参考点在空间内所有可达位置的集合。对于此并联机构,通过选取动平台上参考点所处附近空间的点的集合,判断并找出满足3条支链杆长参数约束要求的点集,这些点集共同组成其工作空间,此时通过逆解即可求得其工作空间。

本文使用蒙特卡洛算法,基于数理统计理论中的概率与统计的思想,对该机构工作空间姿态进行求解,以逆解方程为约束条件,找出满足主动构件参数及运动副约束要求的点集。

建立动平台关于z轴的位移d、绕x轴的转角γ、绕y轴的转角β目标函数如下:

(16)

蒙特卡洛算法的主要步骤为:

1)设定动平台所处的外接圆半径r、静平台所处的外接圆半径R以及驱动装置推动移动副发生相对位移的范围。

3)将得到的末端输出位姿坐标进行记录,并利用Matlab软件将所有的位姿坐标绘制成图6所示的工作空间。

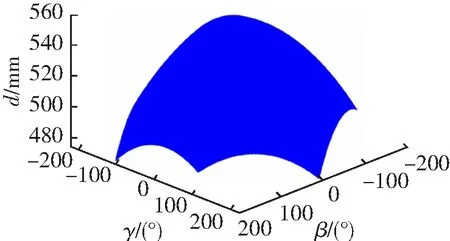
(a)工作空间三维图

该机构运动尺寸参数设定如表4所示。

表4 并联机构运动尺寸参数Tab.4 Motion parameters of parallel mechanism

由图6可知,在给定的尺寸参数和运动参数下,机构动平台绕x轴旋转角度β∈[-190°,190°],绕y轴旋转角度γ∈[-215°,215°],沿z轴移动距离d∈[475,560]。同时可看出,此并联机构具有较大的姿态工作空间,且工作空间形状较为规则、边界清晰,因此其具备优良的工作性能和良好的应用前景。

4 并联机构的运动仿真

将该并联机构三维模型导入Adams软件,如图7所示。分别对该机构运动副设置连接及约束,添加三条支链中的移动副作为驱动副,杆长变化数学表达式如式(17)所示。通过对该并联机构进行运动学仿真,以观察各构件运动过程中是否发生干涉,从而验证此机构设计的合理性。

图7 2-SPS/PRR机构虚拟样机Fig.7 Virtual prototype of 2-SPS/PRR parallel mechanism

(17)

输出位于动平台上动坐标系原点的位姿曲线,见图8所示。

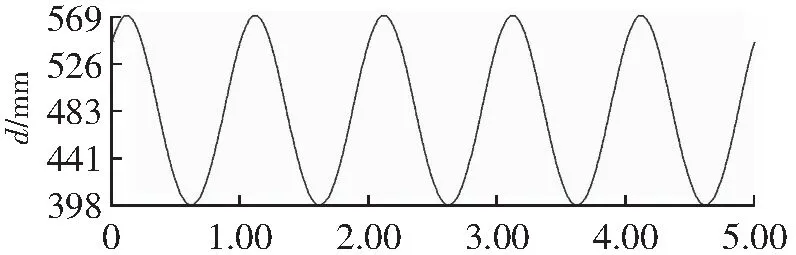
t/s(a) 动平台沿z轴位移变化曲线

通过运动学仿真曲线可知,在5 s时间内,动平台旋转角度α的变化范围为2°～12°,旋转角度β的变化范围为-14°～15°,动平台在Z方向上的位移变化范围为398～569 mm,且在Adams仿真运动过程中机构未发生干涉,运动平稳。

5 结论

1)提出了一种2-SPS/PRR并联机构,通过机构拓扑学理论得出2-SPS/PRR并联机构具有一平移两转动3个自由度,并根据Yang和Sun提出的更具有一般性的DOF公式,验证其正确性。

2)通过建立动、静坐标系,利用封闭矢量法建立运动学逆解模型,并进行算例求解。使用多种群遗传算法得到复杂正解计算的数值解,其正逆解算例相互验证。2种计算方法对并联机构的运动学分析具有十分有效的参考意义。

3)基于蒙特卡洛法,用Matlab软件求解得到其工作空间,从工作空间图中可以看出其工作空间大且连续。用Adams软件建立该机构模型,并对动平台动力学仿真,可看出其运动性能良好,对机构的实际应用具有重要意义。