外贴FRP加固RC短梁抗弯承载力公式

杨泽堃,方圣恩,1b*,吴应雄,江星

(1.福州大学a.土木工程学院;b.土木工程防震减灾信息化国家地方联合工程研究中心,福建 福州 350108;2.福建省榕圣市政工程股份有限公司,福建 福州 350011)

由于钢筋的腐蚀,导致许多基础设施的承载力不能满足正常使用的需求,需要寻找一种材料来进行加固和修复[1]。纤维增强复合材料(fiber reinforced polymer,FRP)作为钢筋混凝土(reinforced concrete,RC)梁、板和柱的修复和加固材料,其承载力加固的效果在实际工程中得到广泛验证[2-4]。FRP材料的抗拉强度高、耐腐蚀性能和耐久性能好,加固后基本不增加结构的自重和尺寸,同时施工便捷,无须借助大型施工设备,可以延长结构的使用寿命[5-8]。

RC梁根据跨高比可分为浅梁、短梁和深梁:其中跨高比(梁的计算跨度与梁截面高度)大于5的为浅梁,介于2到5之间的为短梁,小于等于2的为深梁。目前已经开展了许多通过在RC浅梁梁底外贴FRP布进行抗弯加固的试验研究,结果表明外贴FRP布可以显著地提高浅梁的抗弯承载力[9-10],但有关FRP加固RC短梁的研究较少。王廷彦等[11]进行了考虑混凝土强度、纵筋配筋率和纤维布层数下的加固短梁受弯性能试验研究,发现纤维布层数的增加可以显著提升梁的极限荷载。何亚军[12]通过对外贴CFRP加固RC短梁受弯性能的试验研究,推导了加固短梁正截面受弯承载力公式。值得一提的是,现有文献中FRP加固短梁抗弯承载力的计算公式推导中大多采用GB 50010—2010《混凝土结构设计规范》[13]中的混凝土受压本构模型,但由于该模型不存在下降段,与实际情况不同,导致计算与试验结果间存在误差。此外,由于FRP布与混凝土界面存在着界面黏结剪应力,钢筋屈服后混凝土弯曲裂缝不断开展,裂缝附近的应力集中会导致界面剥离破坏,即中部裂缝剥离破坏。这种破坏形式经常发生在外贴FRP布抗弯加固短梁中,因此需要对这种破坏模式的计算模型进行推导。

有鉴于此,为准确模拟混凝土受压应力-应变曲线,本文采用了更贴近实际、带有下降段的Hognestad应力-应变曲线[14],进行外贴FRP布加固RC短梁的抗弯承载力公式推导。推导过程考虑了FRP布未被拉断的适筋破坏、FRP布被拉断的少筋破坏、超筋破坏和剥离破坏等4种破坏形式[12],最后通过与既有试验梁的数据进行对比,验证所推导公式的适用性。

1 外贴FRP布加固RC短梁抗弯破坏形态

以跨中受集中力作用的RC简支短梁为例,于净跨内梁底面外贴FRP布进行加固,通常发生如图1所示的4种破坏形态。

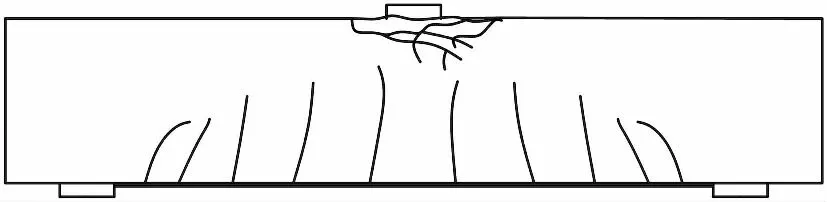
(a) FRP布未被拉断的适筋破坏形态

1)FRP布未被拉断的适筋破坏:当FRP加固量合适,在加载的过程中RC短梁的受拉钢筋先达到屈服,而后随着荷载的增大,受压区混凝土被压碎,短梁发生破坏,纤维布始终未被拉断,如图1(a)所示。

2)FRP布被拉断的少筋破坏:由于FRP的加固量过低或者纵向受拉钢筋的配筋率较小,加载过程中RC短梁的受拉钢筋首先达到屈服状态,而后随着荷载的增加,纤维布的应变随之增大,最后破坏时FRP被拉断,受压区混凝土未被压碎,如图1(b)所示。

3)超筋破坏:当RC短梁纵筋配筋率或配布率较高时,加载过程中易发生纵筋未屈服、FRP未被拉断,但受压区混凝土被压碎的超筋破坏形态,如图1(c)所示。

4)剥离破坏:由于受弯裂缝张开较大,在裂缝附近形成局部界面黏结应力集中而发生剥离破坏。加载过程中短梁的受拉纵筋屈服,梁顶混凝土被压碎,FRP未达到极限抗拉强度而发生剥离破坏,如图1(d)所示。

2 加固短梁受弯承载力公式推导

2.1 计算假定

1)RC短梁符合平截面假定,在达到极限承载力时,裂缝开展较宽,故不考虑混凝土的受拉。

2)混凝土受压应力-应变本构关系采用Hognestad建议的模型[14],模型上升段为二次抛物线,下降段为斜直线(图2)。

图2 Hognestad混凝土应力-应变曲线Fig.2 Hognestad’s concrete stress-strain curve

上升段:

(1)

下降段:

(2)

式中:fc为峰值应力;ε0为峰值应力对应的应变;εcu为极限压应变。

3)考虑到钢筋屈服之后的强化阶段,故钢筋的应力-应变曲线采用带强化段的双折线模型(图3)。

图3 钢筋应力-应变曲线Fig.3 Stress-strain curve of steel bar

当εs≤εy时,

σs=Esεs

(3)

当εy≤εs≤εs,u时,

σs=fy+(εs-εy)E's

(4)

式中:fy为钢筋的屈服强度;εy为钢筋屈服应变;Es为钢筋弹性模量;E's为钢筋强化阶段对应的切线模量。要说明的是,除了带强化段的双折线模型,也可以采用理想弹塑性模型,但后者通常使得计算结果偏于保守。

4)考虑到FRP布为受拉脆性材料,其材料本构采用线弹性模型

σf=Efεf

(5)

式中:σf为FRP布的受拉应力;Ef为FRP布弹性模量;εf为FRP布受拉应力为σf时对应的受拉应变。 暂不考虑FRP布的厚度。

以上假定均满足外贴FRP抗弯加固RC短梁的计算要求。

2.2 计算模型和公式推导

图4为梁底外贴FRP布加固后的短梁受弯承载力计算模型,将受压区混凝土的应力图形替换成等效矩形应力图形,由此求出受压区混凝土等效矩形应力图系数α1、β1。

图4 梁底外贴FRP加固短梁受弯承载力计算模型Fig.4 Calculation model of flexural capacity for short beam strengthened by FRP sheets

1)当εc≤ε0时,可得混凝土受压区压应力合力为

(6)

合力作用点到中和轴距离为

(7)

式中:k1、k2为混凝土应力-应变曲线系数。

由GB 50010—2010《混凝土结构设计规范》[13]可知,可以采用等效应力图形来代替受压区混凝土的理论图形,此时需满足混凝土压应力合力大小相等和两图形受压区合力作用点不变这2个条件。

按照等效条件,可得

α1fcbx=k1fcbxc

(8)

x=2(xc-yc)=2(1-k2)xc

(9)

令

(10)

则

(11)

式中:α1、β1称为等效矩形应力图系数。

2)当ε0≤εu≤εcu时,

(12)

由1)同理可得,

(13)

(14)

(15)

根据式(10)、式(11)、式(14)、式(15)可以求出不同受压区混凝土压应变对应的值,为方便计算,列于表1。

表1 不同受压区混凝土压应变对应的α1、β1值[7]Tab.1 α1 and β1 of compressive strain of concrete at different compressive area[7]

由短梁受弯承载力计算模型可知

α1fcbx=σsAs+σfAf

(16)

(17)

随着梁跨高比的减小,跨中正截面的应变分布越来越不符合平截面假定,内力臂逐渐减小。短梁介于浅梁和深梁的过渡范围,因此需要引入内力臂修正系数来对符合平截面假定的浅梁公式进行修正。GB 50010—2010《混凝土结构设计规范》[13]提供了内力臂的修正系数。

(18)

式中:l0为短梁计算跨度;h为短梁截面高度。

2.3 不同破坏形态计算公式推导

1)FRP布未被拉断的适筋破坏。

结合图4和相似三角形定理,可得

(19)

(20)

(21)

(22)

由表1可获取混凝土达到极限压应变时对应的α1、β1,将其代入

α1fcbβ1xc=σsAs+σfAf

(23)

而后将式(21)、式(22)代入式(23)中,得到一个只含未知数的方程,求解得到受压区高度。

将xc代入式(17),可得

(24)

2)FRP布被拉断的少筋破坏。

结合图4和相似三角形定理,可得

(25)

(26)

根据力和弯矩平衡条件可知

α1fcbβ1xc=σsAs+σfAf

(27)

(28)

与FRP布未被拉断的适筋破坏情况不同,FRP布被拉断的少筋破坏情况下,受压区混凝土未达到极限压应变,因此在计算时不能取混凝土达到极限压应变时所对应的α1、β1。由于εc未知,根据表1先假定一个εc值,由此获取对应的α1、β1值;将εc分别代入式(25)和式(27)中,求出对应的xc,若二者不等,则继续调整εc的值,直至二者接近相等为止;最后将求得的β1、xc代入式(28)中,即可得到抗弯极限承载力。

3)超筋破坏。

结合图4和相似三角形定理,可得

JDR-30DB绞车是一种交流变频控制的齿轮传动单轴绞车，主要由大功率交流变频电动机、小功率送钻电机(含减速机)、大减速箱、大联轴器、小联轴器、气胎离合器、液压盘刹、滚筒轴、绞车架、气控系统、润滑系统、控制箱等单元部件组成。绞车结构见图1所示。

(29)

(30)

由表1可获取混凝土达到极限压应变时对应的α1、β1,而后将式(29)和式(30)代入式(27),得到受压区高度xc,进而将xc代入式(28)即可求得抗弯极限承载力。

4)剥离破坏。

本文根据文献[15]建议的FRP加固RC梁剥离破坏的计算公式,结合跨高比对加固短梁的影响,提出了短梁发生纤维布剥离破坏时,FRP布剥离应变εfe的计算公式

(31)

式中:Ef为FRP布的弹性模量;tf为FRP布的厚度;Ld为FRP端部到最大弯矩截面的长度;fi为混凝土抗拉强度;βw为宽度修正系数。

(32)

式中:bf为FRP的宽度;bc为钢筋混凝土梁的截面宽度。

将式(31)计算所得的εfe代入式(20),解得受压区高度xc,再代入式(21)、式(22)中,可以得到受拉钢筋和FRP布的应力,最后将所求得的xc、σx、σf代入式(28),得到发生剥离破坏时加固短梁的抗弯极限承载力。

3 试验算例验证

文献[11-12,16-17]采用CFRP布对RC短梁进行抗弯加固,研究了外贴FRP对RC短梁破坏形态和极限承载力的影响。为验证本文所推导公式的适用性,选取文献[11-12,16-17]中共计13根包含不同破坏形态的RC短梁(表2),其中构件编号W4-20-4-1、W4-30-4-1、W4-40-4-1、W3、W4、W5、W4-C1-20-4-1、W4-C1-30-4-1、W4-C-1-30-4、W5-C-1-30-4、W4-C-1-30-8和W4-C1-40-4-1为少筋破坏,其破坏形态为受拉钢筋屈服,FRP被拉断,受压区混凝土未被压碎;W4-30-6-1和W4-30-8-1为适筋破坏,其破坏形态为受拉钢筋屈服,受压区混凝土被压碎,FRP未被拉断;W4-C-1-30-6、W4-C-1-30-8、W4-C1-30-6-1和W4-C1-30-8-1为剥离破坏,其破坏形态为受拉钢筋屈服,受压区混凝土被压碎,FRP发生剥离。

表2 外贴FRP布抗弯加固短梁试验数据Tab.2 Experimental results of flexural behavior of short beams strengthened by externally bonded FRP sheets

外贴FRP布抗弯加固短梁试验数据见表2,试验梁的试验值与理论计算值见表3。

表3 试验值与理论计算值比较Tab.3 Comparison of experimental results with calculated values

限于篇幅,此处选取W4-30-6-1的短梁进行演示计算。已知短梁W4-30-6-1外贴了一层CFRP布,梁截面尺寸为b×h=150 mm×500 mm,跨高比l0/h=4。纵筋采用4根直径为12 mm的HRB400钢筋,fy=520 MPa,fc=21.91 MPa,ff=3 512 MPa,t=0.167 mm,试验得到的极限弯矩为119.63 kN·m。

由表1可知对应的α1=0.91、β1=0.87,将其代入式(23)可得混凝土受压区高度xc,再将求得的xc代入式(24),得到极限弯矩Mu=124.37 kN·m,与试验实测值误差仅4%,说明推导的公式具有良好的准确度。其余试验梁的详细参数和试验值,列于表2,采用本文所推公式计算的理论值与试验值的比较列于表3。由表3可见,试验值与理论值之比的平均值为1.03,标准差为0.04,变异系数为4.22%,说明计算值与试验值离散性较小,所推导公式可作为外贴FRP布加固短梁抗弯承载力计算的参考。

4 结论

本文基于Hognestad建议的混凝土本构关系,推导了适用于外贴FRP布加固RC短梁的抗弯承载力计算公式,考虑了FRP布未被拉断的适筋破坏、FRP布被拉断的少筋破坏、超筋破坏和剥离破坏4种破坏形式,最后通过理论计算与试验梁的测试值对比验证了所推导公式的适用性。得到了如下结论:

1)采用Hognestad本构模型更符合实际情况,适用于外贴FRP抗弯加固RC短梁在不同破坏模式下的抗弯极限承载力计算,计算结果与试验值吻合良好,离散性较小。

2)考虑到短梁处于浅梁和深梁的过渡范围,引入内力臂修正系数能够较好地考虑到短梁的内力臂随着跨高比的减小而减小的特点,计算针对性较强。

3)本文公式验证采用的是外贴CFRP布的加固短梁,但所推导的公式同样也适用于其他类型的纤维布,只需先求出FRP布的实际应变,再结合FRP布的弹性模量进行计算即可。