医用多因素分析及SPSS操作课程教学经验探讨

裴磊磊,赵亚玲,康轶君,朱永生

(西安交通大学医学部: 1.公共卫生学院;2.法医学院,陕西 西安 710061)

随着医学研究深度和广度不断发展,新的疾病预防及诊疗模式不断涌现,数据来源更加多元,包括临床数据、多组学数据、环境暴露、遗传信息、生活习惯、地理空间信息、社交媒体及其他多种与个体健康和疾病状态相关的高维数据,要从看似复杂无序的数据中发掘隐含的内在规律, 以指导医学决策,对统计学提出了新的挑战[1]。而医学基本统计方法仅限于单变量描述和推断,无法深度挖掘多个相依因素(变量)之间的关系或具有这些因素的样本(个体)之间关系。因此,医用多因素统计分析方法(Medical multivariate statistical analysis)应运而生,它是一种可以最大程度利用既有信息进行模型构建的方法,达到简化复杂数据结构,阐明主要研究问题的目的,目前已成为医学统计学的重要组成部分,在公共卫生学、临床医学、药学、护理学等领域的数据分析中发挥了不可替代的作用[2]。

多因素统计分析是数理统计学的一部分,其中包含了抽象的概念及理论、烦琐的矩阵代数计算、复杂的数学推导论证等,对于数学功底薄弱的医学生而言,学习难度相对较大。同时多因素统计分析也是一门实践性和应用型非常强的课程,需要借助计算机软件才能完成计算验证过程,统计理论学习需要与计算机软件教学同步进行。目前可供选择的统计软件有SPSS、SAS、STATA、R语言等,其中SPSS致力于简便易行,尤其适合临床医学、药学、护理学等专业统计学基础薄弱的科研工作者,其操作能够快速上手、基本满足科研需求。笔者所在教学团队基于多年教学实践,针对医学专业研究生总结编写了《医用多因素统计分析及SPSS操作》[2],旨在提升医学生对医学相关数据的综合分析应用能力,本文基于学生的实际情况和该课程的特点,探讨了医学多因素统计分析课程的教学方法并总结了以下教学经验,以达到抛砖引玉的作用,提高学生学习的积极性和解决实际问题的能力。文章所涉及的统计分析例题均来源于笔者团队编写的教材《医用多因素统计分析及SPSS操作》,统计分析均在SPSS 18.0中实现[2]。

1 医用多因素统计分析及SPSS操作教学要有贯通式思维

多因素统计分析理论复杂抽象,方法种类繁多,不同方法之间前后紧密相连,学习当前统计方法同时紧密结合前面已学的统计理论,相互比较,相互印证,前后贯通,帮助学生形成贯通式的统计思维[3]。例如在学习多因素方差分析方法时,可以结合多重线性回归分析理论,利用线性模型的原理阐述多因素方差分析的思想[4]。方差分析的研究设计包括了析因设计、协方差设计、重复测量设计等多种形式,各种类型的方差设计形式都可以利用回归模型表示。以两因素析因设计(即I×J析因设计)为例,表示有两种处理因素,第一种处理因素A有I个水平,第二种处理因素B有J个水平,析因设计线性模型表示为Y=α+β1X1+β2X2+β3X1X2+ε,其中α是截距,β1、β2和β3为待估的回归系数,ε为独立且服从正态分布的残差。以教材中例3-1析因设计方差分析数据为例,采用多重线性回归分析,研究药物治疗X1和给药时间X2对小鼠肝脏组织铁浓度的影响。当X1=1时表示试验组,X1=0时表示对照组;当X2=1时表示给药后30min,X2=0时表示给药后60min。

首先建立析因设计方差分析SPSS数据文件,药物表示实验组和对照组,时间表示给药后30min和60min,铁浓度表示肝脏组织铁浓度,执行 Analyze→General Linear Model→Univariate命令,选择药物和时间的主效应、交互效应,单击对话框下方的OK按钮,即可得到析因设计方差分析结果。

然后建立多重线性回归分析数据库,药物治疗X1和给药时间X2分别为二分类变量,设置两个哑变量及交互效应引入模型中。首先考虑Analyze→Regression→Linear,打开Linear模块后,依次选择因变量和自变量,单击对话框下方的OK按钮,获得相应结果。

例3-1中数据进行多重线性回归分析和析因设计的方差分析的结果完全一致,线性回归引起的变异可以进一步分解为药物、时间及交互作用三部分变异。将两种方法的结果列于表1中,可见多因素线性回归中回归变异SS等于药物、时间、交互效应三部分SS之和,即多因素线性回归中回归变异可以进一步分解为析因设计方差分析中药物、时间、交互效应三部分,两种方法总变异完全相等。

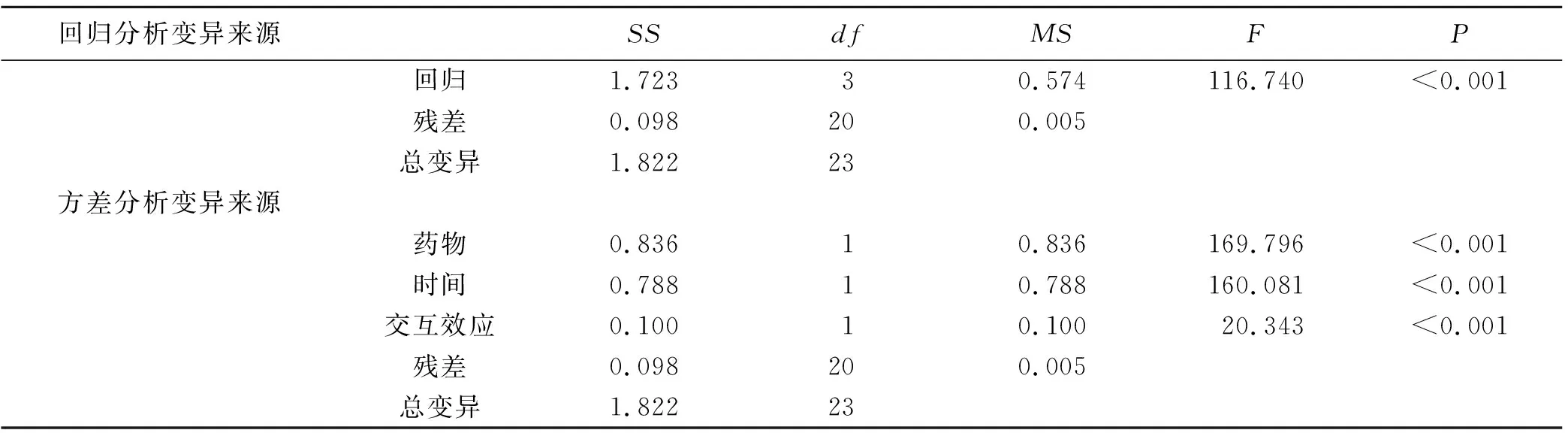
表1 例3-1多重线性回归和析因设计方差分析比较

将原始数据的4组数据的均数整理成表2,得出药物处理不同水平、时间效应不同水平的单独效应、主效应和交互作用。当药物固定在实验组时,时间的单独效应为0.492;当药物固定在对照组时,时间的单独效应为0.233。同理,时间固定在30min时,药物的单独效应为0.244;时间固定在60min时,药物的单独效应为0.503。依次得到药物治疗和给药时间的主效应分别为(0.244+0.503)/2=0.374和(0.492+0.233)/2=0.363。药物治疗和给药时间的交互效应为(0.503-0.244)/2=(0.492-0.233)/2=0.129。

多重线性回归系数估计结果见表3,药物治疗在60min时的单独效应为α+β1+β2+β3-α-β2=0.503,药物治疗在时间30min时的单独效应为α+β1-α=0.244,因此得到药物治疗主效应为(2β1+β3)/2=(0.244+0.503)/2=0.374,同理得到给药时间的主效应为(2β2+β3)/2=0.363,药物治疗与给药时间的交互效应为β3/2=0.258/2=0.129,P值都小于0.001,说明药物治疗和给药时间对小鼠肝脏组织的铁浓度都有影响而且存在交互效应,与析因设计方差分析结果一致。

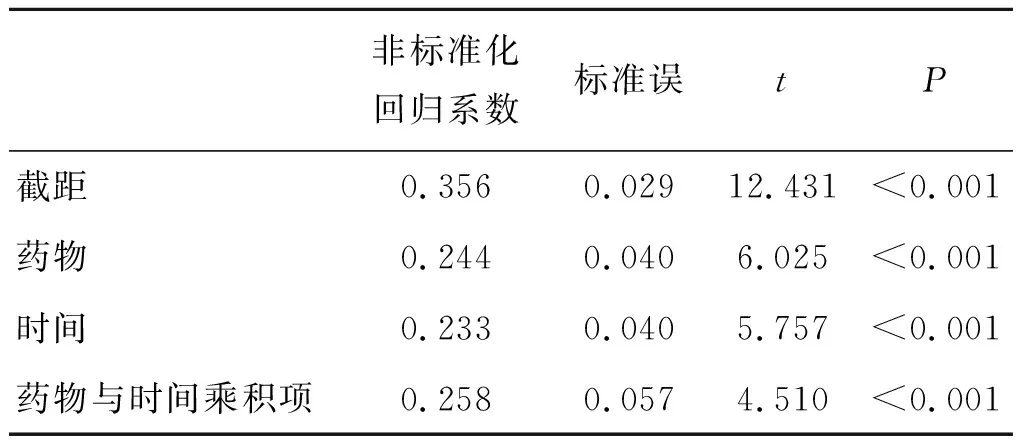
表3 例3-1线性回归系数结果

此外,重复测量设计、协方差分析、交叉设计等都可以采用多重线性回归分析的思路进行分析,各部分方法前后相互联系,相互印证,培养贯通式思维能力,基于教材示例数据,讲授每一种统计分析方法可以紧密联系所学统计理论方法,前后内容相互衔接,既可以帮助学生回顾梳理统计学基本理论方法,又能加深对新的统计理论方法的理解。

2 医用多因素统计分析及SPSS操作教学要有类比的思维

在医学研究中,研究者有时会尽可能多地收集信息,数据来源更加多元,包括门诊信息、住院信息、常规体检数据、居民健康档案管理数据等,这样涉及更多的研究指标和变量,造成数据维度灾难,数据分析更加复杂。多因素统计分析中聚类分析、主成分分析和因子分析既能实现不同变量的聚类,达到降维的目的,简化数据结构,又能发现不同变量之间的整体效应。因此,在分析此类高维数据时,可以选用不同的多因素降维方法相互比较,培养统计学类比的思维能力,理解掌握统计学精髓。以教材中例9-1数据为例,分析500名青少年的健康相关结局,由于变量包括了总智商(Full scale intelligent quotient, FSIQ),行为问题总分(Total scores of Problem, Problem_ts),收缩压(Systolic blood pressure, SBP),舒张压(Diastolic blood pressure, DBP),按WHO标准化的身高性别、年龄别Z评分(Height-for-age and -sex Z score, HAZ),和体质指数性别、年龄别Z评分(Body mass index-for-age and -sex Z score, BAZ)等指标,采用适当多因素统计分析中的降维方法分析青少年人群的健康现况。

可以首先采用K-means聚类分析,考虑到不同变量有不同的量纲,在数量级上存在较大的差异,为了消除各变量量纲和数量级不同对聚类结果可能的影响,需要先对变量进行标化处理。变量的标化可以采用SPSS中 Analyze→Descriptive Statistics→Descriptives功能将标化后的变量另存为新变量。然后选择菜单Analyze→Classify→K-Means Cluster Analysis,打开K-Means Cluster Analysis模块后,将6个标化后的变量选入Variables框。将变量pc选入Label Cases by即个案标注依据框。将聚类亚组数Number of Clusters改为3。单击对话框下方的OK按钮,得到相应结果。

表4给出了聚类分析最终的类别中心点,该值为各个类别中各变量的均值。类别1人群的特征是智商水平在人群平均水平,行为问题发生率较低,而其他体格特征如BAZ、血压等均处人群较高水平;类别2人群的收缩压和舒张压低于人群水平特征,智商和体格相关指标高出平均水平,尤其是行为问题最为突出;类别3在所有健康指标的均值都低于平均水平。结果提示在改善青少年健康状况的干预政策的制定过程中,要重点关注类别1人群的心血管健康,类别2人群中的精神卫生健康,类别3中所有的青少年。

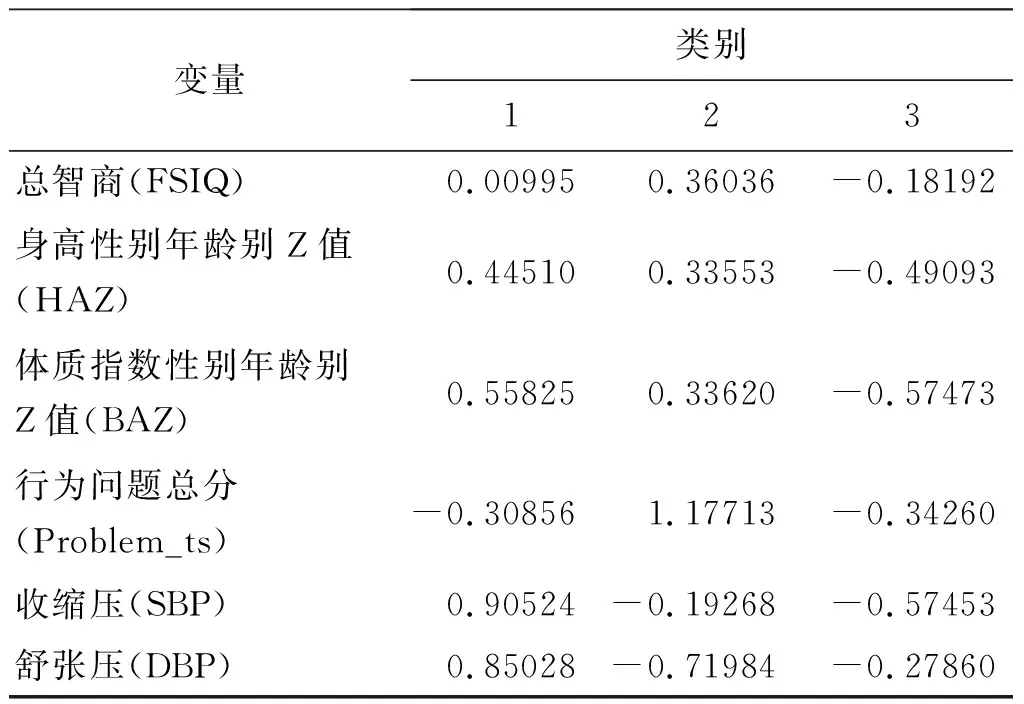
表4 聚类分析不同类别中心点

之后采用主成分分析和因子分析再次分析,依次选择主窗口主菜单中的Analyze→Dimension Reduction→Factor,在打开的主对话框中选左边变量名列表中的6个变量到右边的Variables(变量)框中,最后单击主对话框下方的OK按钮,即可获得相应结果。

KMO(Kaiser-Meyer-Olkin)统计量为0.497,Bartlett’s球形检验P<0.001,提示这6个指标数据适宜进行主成分分析。按照特征根从大到小列出了所有的主成分。其中,第一个主成分的特征根为1.815,解释了30.25%的总变异;第二个主成分的特征根为1.332,解释了22.19%的总变异;第三个主成分的特征根为0.971,解释了16.18%的总变异,前三个主成分共解释了68.62%的总变异,因此,最终选择三个主成分作为结果。

表5主成分特征向量结果显示,第一主成分的特征是智商水平和行为问题影响较小,而其他体格特征如BAZ、血压等均处人群较高水平,与聚类分析类别1相似;第二主成分对所有健康指标具有影响,与聚类分析类别3相似;第三主成分对收缩压和舒张压影响较小,尤其是行为问题最为突出,与聚类分析类别2相似。结果也说明了在改善青少年健康状况的干预政策的制定过程中,不同类别应关注不同的指标,比如第一主成分的心血管健康,第二主成分的精神卫生健康,第三主成分所有的健康指标。该例题说明聚类分析和主成分分析都能够实现数据或变量降维,简化数据结构,本质上是相同的。

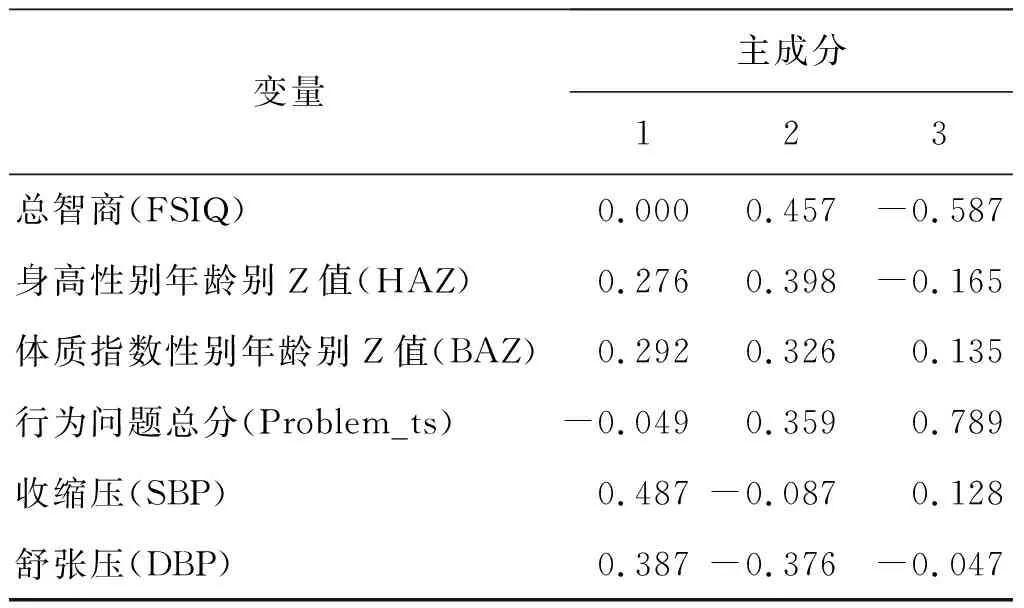
表5 主成分分析相关矩阵的特征向量

基于以上例题的分析,提示我们在教学过程中,针对多因素统计分析方法的学习,可以根据已学统计理论知识,从不同角度类比联想,采用新旧不同方法由浅入深,同时进行结果分析比较,既能帮助学生理解掌握新知识,又能进一步复习巩固旧知识,可以取得事半功倍的教学效果。

3 医用多因素统计分析及SPSS操作教学要有整体性思维

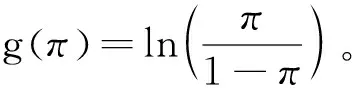
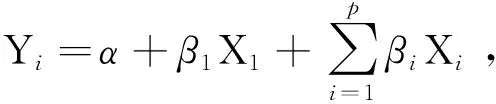
多因素统计分析方法研究的是多个因素间的相互关系或彼此影响,不同方法不是孤立的,有着密切的联系。例如本教材中多重线性回归和Logistic回归可以抽象为广义线性模型的一种,而聚类分析、主成分分析和因子分析可以抽象为数据降维方法,整体性思维意味着应对不同方法进行比较归类,明确他们之间的区别和联系,抽象概括统计规律性,这样既帮助学生巩固了所学知识,又加深了学生对多因素统计分析理论的理解和记忆。

4 医用多因素统计分析及SPSS操作教学要有实践的思维

多因素统计分析应从医学研究生和科研工作者的实践应用出发,在适当掌握一定理论的基础上,开展以问题为中心的学习模式,以学生为主体,在教师的指导下,由学生围绕身边的相关医学问题进行科研选题。根据研究目的进行科学的研究设计、现场调查、数据收集,甄选多因素分析方法形成统计分析方案;在研究实施过程中和完成后收集原始研究资料、整理资料、量化资料,建立分析数据库,要求数据完整、准确,样本量足够;选用合适的多因素分析方法利用SPSS软件对数据资料进行全面分析,对结果进行解读阐述,与文献的分析过程进行比较,对其分析做出评价。

例如妊娠期糖尿病(Gestational Diabetes Mellitus,GDM)是由于妊娠后母体糖代谢异常而首次发生的糖尿病,是妊娠期常见的并发症之一,与胎儿畸形、宫内发育迟缓、新生儿窒息、早产、巨大儿等多种新生儿不良出生结局存在密切关联[7-8]。针对该问题,要求学生采用病例对照研究设计,自行设计问卷调查某医院孕6～13+6周的单胎孕妇,进行孕期体检,愿意且能够签署知情同意书。收集数据包括孕妇的文化程度、孕期饮用咖啡和饮茶、孕前体重指数、糖尿病家族史、年龄胎次、孕期糖化血红蛋白等7个因素的资料,要求学生收集数据后,整理资料、量化资料,建立分析数据库,使用合适的统计分析方法进行分析,并给出临床建议。

根据研究目的和数据特点,本研究可以采用Logistic回归进行多因素分析,确定孕妇孕期并发糖尿病的主要影响因素。多因素分析结果发现高龄初产妇、糖尿病家族史、糖化血红蛋白、超重、肥胖与孕期并发糖尿病正相关,从临床角度看,减少高龄初产妇、控制体重及糖化血红蛋白等指标,对预防孕期并发糖尿病具有重要意义。本例以解决实际医学问题为突破口,引导学生带着问题有针对性地了解多因素Logistic回归分析的数学模型和分析的基本思路,既提高了学生多因素统计分析知识的运用能力,又能激发学生参与课堂的热情,满足了医学生理论联系实际的需求。

5 结语

医用多因素统计分析方法在医学研究中具有重要的作用,是医学科学研究中不可或缺的重要分析工具,同时极大地促进了医学科学发展。如何高效组织医用多因素分析课程教学,如何提高教学效果和学生学习的积极性是非常值得讨论研究的问题。本文基于前期教学经验,并结合团队编写的《医用多因素统计分析及SPSS操作》探讨了教学过程中的基本规律和特征,总结运用了贯通式思维、类比的思维、整体性思维和实践的思维等,将多因素统计分析理论前后有机结合,明确不同方法的区别和联系,抽象整合不同的统计学理论方法,紧密联系医学实际问题,既能帮助学生掌握多因素统计分析的精髓和内涵,又能提高学生解决实际问题的能力。同时对教师也提出了更高的要求,需要不断学习新理论,不断总结经验,进一步提高教学质量。