考虑移动式储能均衡的微电网群分布式动态协同控制策略
楼冠男,秦 琦,顾 伟,赵 波,陈 哲,洪吟秋
(1.东南大学电气工程学院,江苏省南京市 210096;2.国网浙江省电力有限公司电力科学研究院,浙江省杭州市 310014;3.国网宜兴市供电公司,江苏省宜兴市 214200)
0 引言
微电网群作为多个微电网互联互供构成的一体化网络,已成为提升分布式电源(distributed generator,DG)渗透率、改善供电可靠性以及增强电网弹性的主要途径[1-2]。当发生大负荷投切或DG 故障退出时,为应对微电网群供需功率不平衡的问题,需动态改变系统拓扑并加以紧急控制提供频率电压支撑,确保最大限度地对重要负荷持续供电。然而,受限于可控DG 容量及新能源波动性,孤岛特性下的微电网群可能并不足以满足持续供电需求。同时,考虑到故障发生位置的随机性和不确定性,不同故障点存在不同功率缺额需求。因此,有必要在系统中配置一定数量的移动应急电源,主动提升空间灵活性和生存能力[3-4]。
移动式储能系统(mobile energy storage system,MESS)通过移动储能车应急接入分布式发电系统,具有机动性强、响应速度快、运营成本低等一系列优势,可根据系统不同供电需求选择不同接入点,作为灵活性电源实现“即插即用”,更好地适应系统故障后运行工况的复杂变化[5-7]。目前,对于MESS 的 研 究 多 侧 重 于 其 选 址 定 位[8-9]、优 化 配置[10-11],以及从调度层面对含MESS 的微电网故障恢复策略[12-13]展开分析。而在控制层面,MESS 与DG 间的协同控制是实现系统灵活调控的关键。传统的集中式控制需要强大的通信和计算能力[14],且存在“单点故障”问题,限制了其应用。分布式控制因其具有高可靠性和灵活性等特点,更适用于集群协同控制。文献[15]考虑了多储能单元的荷电状态(state of charge,SOC)和DG 可用功率,提出一种分布式有功功率协调控制策略,但该方法随着负载增大,调节精度会降低。文献[16]实现各储能以SOC为比例分配功率,并基于比例-积分(proportionalintegral,PI)一致性算法设计多组光储单元的电压恢复二次控制,但控制器瞬态特性较差。文献[17]基于分布式一致性算法,实现了微电网群级频率电压协同控制及微电网间储能单元SOC 均衡控制。考虑到微电网群故障后通信条件差、MESS 频繁投切、运行工况多变等因素,且对控制器收敛速度、抗扰动性、通信成本以及MESS 运行效率要求更高,上述控制策略在系统紧急情况下并不适用。
对此,文献[18-19]从提升控制收敛速度出发,采用有限时间一致性策略,使系统频率电压恢复与功率均分在有限时间内实现,但该方法收敛时间受限于系统初始状态,在出现严重故障时效率较低。文献[20-21]对此加以改进,仅由控制参数和通信图保证收敛时间,能更好地适应MESS 频繁投切操作,但所需通信成本仍然较高,且未考虑SOC 均衡控制。文献[22]设计了一次、二次控制策略实现柴储应急电源的协调出力、频率电压恢复以及储能间SOC 均衡,但文中并未涉及应急电源的投切控制。
本文兼顾控制收敛性能与通信成本,针对MESS 应急接入的微电网群提出一种基于事件触发的动态协同控制策略,在保证系统频率/关键母线电压恢复的同时,还实现了各电源间功率均分及MESS 间SOC 均衡。具体创新工作包括:1)提出了基于动态收敛算法的分布式协同控制策略,在排除冗余数据情形下各节点状态量在有限次迭代中收敛至所估计平均值,具有兼顾收敛速度和收敛稳定性的优势;2)提出了基于预同步和供需功率无缝转移的MESS 投入/退出策略,实现MESS 平滑投切;3)引入了事件触发机制以降低通信成本和压力,并分析了控制算法收敛所需满足的稳定性准则。
1 微电网群应急供电方案及控制要求
本章主要阐述了微电网群故障情形下移动式储能组网供电流程与方案,并基于此介绍系统控制目标及要求。
1.1 故障下应急供电方案
正常运行时,微电网间联络开关闭合,系统内各微电网能量互济、互为支撑,以一个整体互联运行,协同各发电单元为负荷供电。当微电网群出现较大且突然的扰动(如大负荷投切、DG 跳闸等),改变了系统原有的发电和用电间平衡,使得系统存在一定程度的供需功率缺额,此时,可通过切除重要程度相对较低的负荷。同时,结合拓扑重构和接入所配置MESS 保证对重要程度更高的负荷供电。具体的应急供电流程可描述如下:
1)故障解列:若系统故障短时间内无法修复,则依据重要负荷位置分布及DG 容量等信息,通过控制联络开关通断调整系统拓扑,将微电网群主动解列为若干正常运行子微网和故障子微网,以尽可能保证对更多重要负荷供电。
2)MESS 接入:根据故障子微网内负荷重要程度、不同节点功率缺额以及道路交通情况等确定MESS 接入点和接入方式,待MESS 到达指定点后接入为故障子微网提供频率/电压支撑,并协同本地DG 单元为重要负荷提供持续电力供应。
3)负荷恢复:在应急接入的MESS 为故障子微网建立可靠的频率/电压支撑后,确保在不超过故障微电网内DG 和MESS 容量上限的情况下,按重要程度对失电负荷进行供电恢复。
4)重新互联:故障消除后,控制联络开关闭合使各微电网重新互联运行,待系统稳定运行一段时间后,各MESS 退出系统。
对 应 于 流 程2),图1 展 示 了4 种MESS 接 入 方案。其中,图1(a)和(b)为单个MESS 接入方案,分别侧重于对MESS 接入路径以及接入点进行优化选择,从而最大限度地缩短负荷失电时间。图1(c)和(d)表示多个MESS 接入的方案,各MESS 互为备用,即使某一个MESS 因道路损坏或拥挤导致无法接入或较慢接入系统,其余MESS 也可以为系统提供应急支撑。图1(c)为多个MESS 集中接入同一点的情形,图1(d)则考虑了多个MESS 分散接入不同节点,先抵达故障子微网的MESS 立即组网为负荷应急供电。
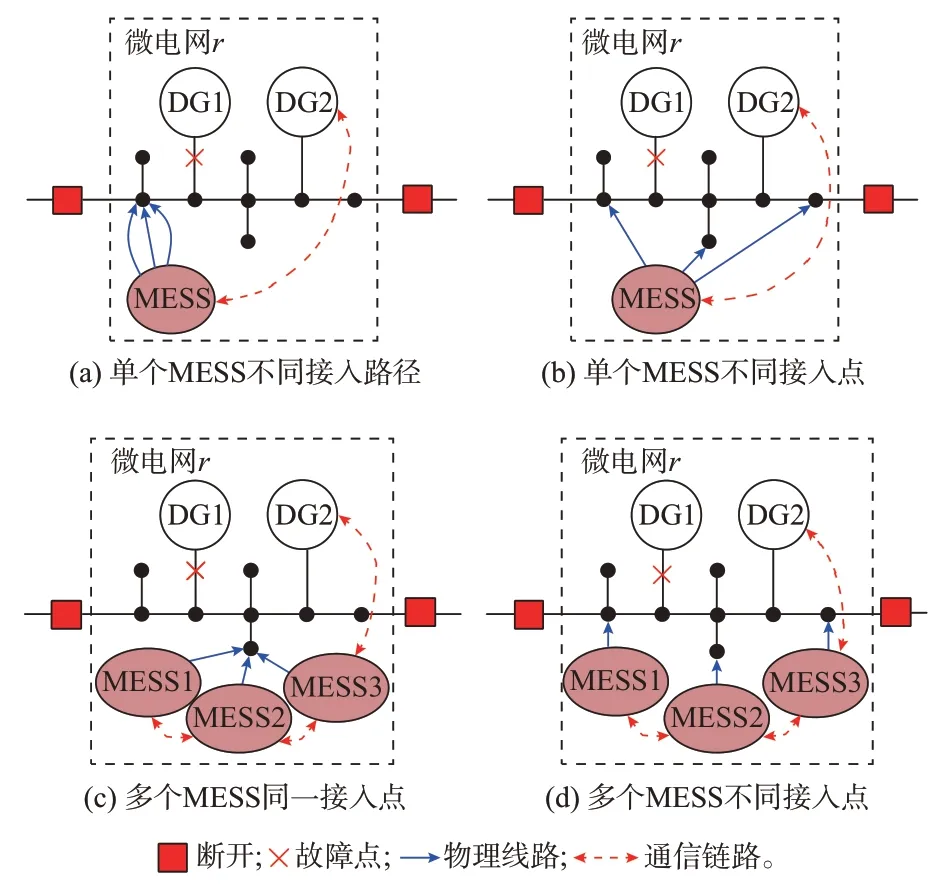
图1 MESS 接入方案Fig.1 Schemes of MESS integration
本文侧重于MESS 控制层面研究。考虑到MESS 应急接入是针对小范围、区域性的故障微电网,因此,假设故障后各MESS 能及时到达所需接入位置。同时,本文采用无线通信技术建立系统通信网络架构,易于临时搭建,能满足不同传输距离要求。此外,针对故障系统不同节点的不同功率缺额需求,为保证故障子微网有足够可调节容量并且以更灵活的方式支撑重要负荷持续运行以及加速恢复失电负载,降低因故障进一步扩大而导致系统崩溃的风险,本文选择图1(d)所示更具灵活性、可靠性和普适性的多个MESS 分散接入方案展开研究。
1.2 控制目标
将若干微电网组成的微电网群系统表示为Γ,并假设各微电网内皆含有可控DG。对于相互连接的微电网X 和微电网Y(X,Y∈Γ),至少各选择一个可控DG 与其中的联络开关共同构成微电网群级通信网络。定义εXY为微电网间的联络开关状态,εXY=0 表示闭合,εXY=1 表示断开,即可根据εXY状态实现微电网间功率的优化分配。而微电网内各可控DG 间则共同形成微电网级通信网络,实现微电网内DG 功率均匀出力。其中,可控DG 采用下垂控制参与频率/电压调节,并实现供需功率平衡需求。微电网X 中第i个可控DG 的输出电压和频率参考值由功率环路确定:

1)正常工况下(εXY=0),互联微电网之间按比例均分有功和无功功率,可等效表示为各微电网平均出力按比例均分,即
式中:(t)表示对应t时刻的变量值;PˉX,i、PˉY,j和QˉX,i、QˉY,j分 别 为 微 电 网X、Y 中 第i、j个DG 的 平 均 有 功和无功功率;i,j=1,2,…,n,i≠j,n为区域内DG个数。
2)各微电网内可控DG 按容量分配有功和无功功率,即

随着故障发生微电网群解列以及MESS 应急接入,各MESS 变流器同样采用式(1)形式的下垂控制主动参与调频/调压,响应系统负荷变化需求。系统通信网络根据联络开关状态发生改变。此时,对于解列的各微电网将不再要求实现群级控制目标1)。而对于故障子微网,把MESS 视作某个可控DG 节点的邻居节点,并与其余DG 进行信息交互。因此,故障子微网内DG 与MESS 需要协同提供稳定的电压/频率支撑,并实现两种类型电源间出力的合理分配,以保证重要负荷持续可靠供电,即在故障恢复阶段仍需满足控制目标2)~4)。此外,由于各MESS 的初始状态、响应速度常存在一定差异,还需要充分考虑接入MESS 的SOC 均衡情况,从而有效避免初始SOC 较低的MESS 在应急供电过程中过度放电而导致设备损坏,保证储能单元运行效率和健康状态,并最大化利用MESS 综合功率和能量容量[23-24]。为此,需满足控制目标5)。
5)在系统恢复阶段保证各MESS 的SOC 均衡。
式中:下标m、l表示MESS 编号;Sr,m为第r个故障微电网中第m个MESS 的SOC。
1.3 控制难点及要求
平均一致性算法作为实现微电网集群协同控制的常用方法,其基于拉普拉斯算子迭代计算,在每次迭代中,邻居节点间不断进行信息交互同步并执行分布式平均,全局节点最终收敛至各节点初始状态量的平均值。该方法虽然具有简单、易于实现等优点,但在迭代过程中全局平均一致性是渐近达成的,其指数收敛速度受通信拓扑结构的显著影响。相关指数系数可量化为代数连通度[25],即通信图拉普拉斯矩阵L的第2 个最小特征值λ2,且λ2越大,收敛速度越快。
此外,在信息处理和传输过程中不可避免地存在时滞,为了便于描述通信延时对一致性算法的影响,将其离散化处理为式(7)形式,即只在本地控制时刻对状态量进行采样和更新。
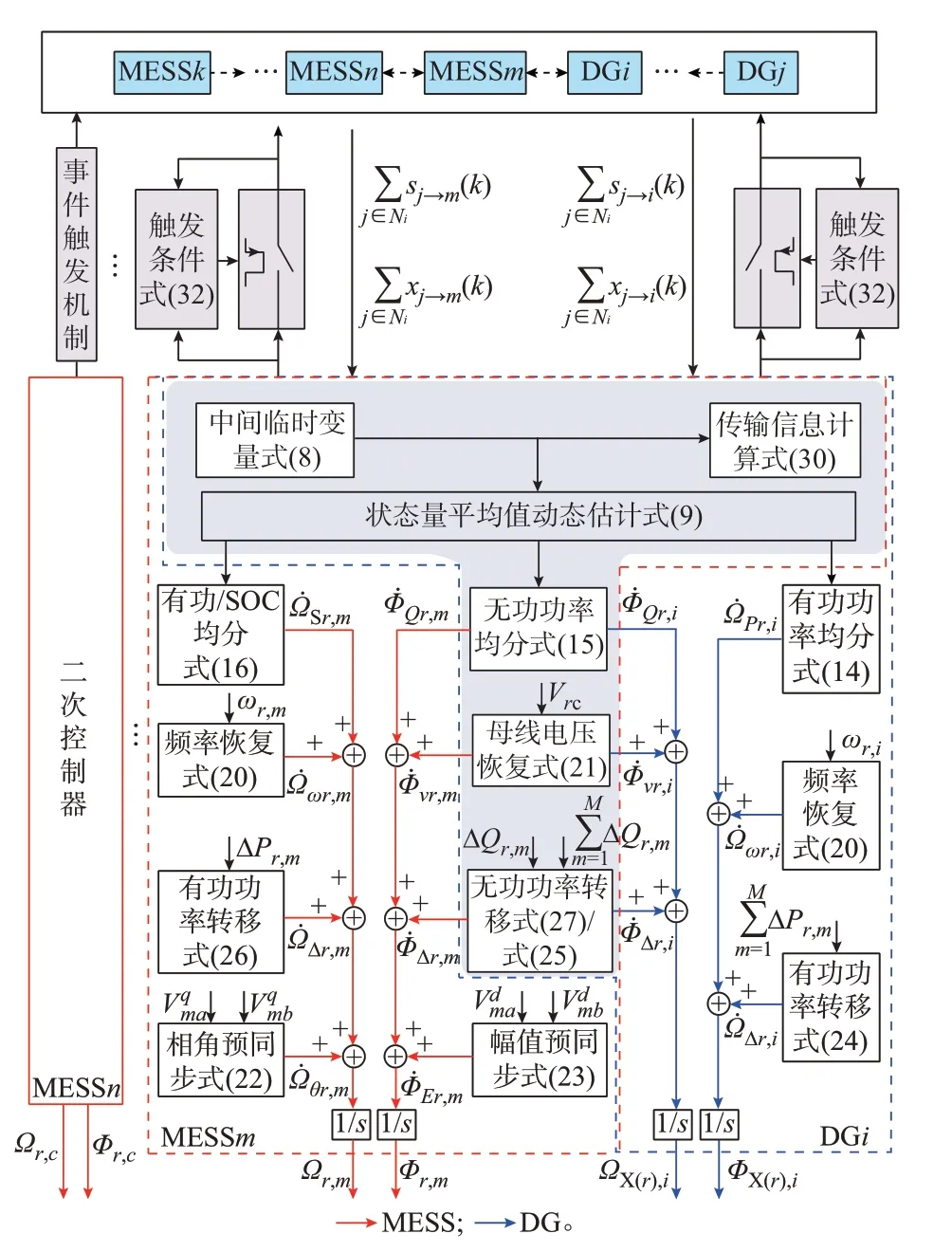
式中:xi(k)为节点i在k步的状态值;aij为节点i与节点j间通信链路权重;τ为时滞。节点i的信息传输时序如附录A 图A1 所示。图中:x1,x2,…,xn为对应采样时刻状态值;Ti为采样时间间隔。由图A1 可知,当τ 鉴于此,系统应急供电场景对所采用控制策略性能提出了更高要求:1)故障子微网内DG 与MESS 协同控制的收敛速度应尽可能快,以加速失电负载供电恢复,同时适应复杂多变的系统工况;2)控制器对通信网络的依赖性应尽可能低,在非理想通信工况下仍保持较强的鲁棒性和容错性;3)应尽可能减小MESS 接入/退出系统时造成的暂态冲击,避免故障进一步扩大或故障二次发生。 为适应系统故障下复杂多变的运行状态,本章设计了微电网群应急协同控制方法,将应急接入故障微电网r的MESS 视作可控DG 的邻居节点,通过各电源本地信息采集和电源间通信交互实现各项控制目标,系统整体控制框架如图2 所示。图中:Ω̇和Φ̇为各项二次控制器,其下标m和i分别对应MESS和DG;Vdma、Vdmb和Vqma、Vqmb分别为MESS 接入点两侧电压的d轴和q轴分量;ΔPr,m和ΔQr,m分别为第m个MESS 需要转移的有功和无功功率。首先,简要介绍动态收敛算法的基本原理[27]和优越性,并基于此对系统各DG 及MESS 的有功和无功功率及SOC状态量进行估计,进而设计相应群间/群内有功和无功功率均分及MESS 的SOC 均衡控制器;其次,利用各电源本地信息设计频率/关键母线电压恢复二次控制策略,保证系统稳定可靠运行;最后,应用预先控制思想提出MESS 无缝投切策略,包括MESS投入运行时的相角/幅值预同步以及退出运行时的有功和无功功率转移策略,从而有效保证MESS 的“即插即稳”。为减小通信成本和通信压力所设计的事件触发机制将在第3 章中介绍。 图2 微电网群应急协同控制整体框架Fig.2 Overall framework of emergency cooperative control of microgrid clusters 本文所采用的动态收敛算法中,节点i的权重信息wi和动态状态量zi被指定为输入量,并引入两个临时中间变量s͂i(k)和x͂i(k)用以辅助计算算法的输出量x̂i(k),即动态状态量的加权平均估计值。另外,定义Ni为节点i的邻居节点集合,si→j和xi→j分别为从节点i传递给邻居节点j但又不包含节点j信息的权重值以及按权重进行加权的状态量平均值,且在初始时刻si→j(0)=wi,xi→j(0)=zi。则在其后的第k次迭代中,对于节点i有: 基于式(10)进一步计算节点i需要传递给各邻居节点的信息,同时,考虑到本地节点的已知信息中包含了部分从邻居节点传来的信息,这部分信息将在当前迭代中被剔除: 随后,各节点估计的加权状态量平均值将收敛到系统的精确平均值。为便于说明,图3 进一步展示了5 节点通信拓扑下节点i前4 次迭代过程中的信息交互。由图可知,第1 次迭代中,节点i与其邻居节点j和m进行信息交互,为避免信息冗余,刚从邻居节点传递到节点i的信息之后将不会从节点i再次返回发送,以此类推,经4 次信息传输,与节点i通信的其余节点都获取了全局状态信息,而在后续迭代中,所传递信息流将与第4 次迭代中信息流保持一致。从上述算法执行过程可以看出,各节点在排除冗余数据并且仅传递本地已知信息的情况下实现全局信息获取,提高信息传播效率,有助于加快收敛速度,系统可以在有限次迭代后达到收敛,所需迭代次数与通信有向图的直径相关,即相距最远的两个节点间的跳数dmax[24]。更重要的是,各节点对信息到达时刻同步性无严格要求,这便可以保证算法控制精度及减少系统不稳定风险。 图3 信息传输过程示意图Fig.3 Schematic diagram of information transfer process 1)有功和无功功率均分控制 考虑到下垂系数与DG 容量成反比,对于微电网X 中第i个DG,分别定义有功和无功功率与其下垂系数的乘积作为两个状态量,即γX,i=mX,iPX,i,ηX,i=nX,iQX,i。则微电网间功率均分的控制目标可以等效转换为控制对应微电网群级通信网络中DG的状态量γX,i、ηX,i收敛至相邻互联微电网Y 内DG对应的平均值γˉY,j、ηˉY,j,而控制过程中的平均值可由γY,j和ηY,j分别代入式(8)和式(9)动态估计得到。 式 中:x͂Y,γj(k)、x͂Y,ηj(k)和s͂Y,γj(k)、s͂Y,ηj(k)分 别 为 估算微电网Y 中第j个DG 功率状态量平均值时的中间临时状态量和临时权重信息。由于待估计的状态量平均值为标准算术平均值,本文默认将各状态量权重信息wi赋值为1。微电网群级通信网络节点间不断进行信息交互和迭代计算,γX,i和ηX,i将逐渐收敛于精确的平均值。因此,结合联络开关的状态,互联微电网间有功和无功功率均分二次控制器分别设计为: 式中:kPXY,i和kQXY,i为积分系数。 同样地,各微电网内功率均分的控制目标可以等效转换为控制微电网内各DG 的状态量γX,i、ηX,i收敛至对应平均值。微电网X 内有功和无功功率均分控制器可分别建立为: 式中:kPX,i和kQX,i为积分系数。 系统发生故障后各微电网解列,式(12)和式(13)中开关状态量εXY=1。各MESS 作为应急电源接入故障微电网r,同时系统通信网络相应更新,MESS 需要协同故障微电网r内各DG 按照容量大小出力实现对重要负荷的电力供应。由于可控DG与MESS 在控制模式上具有兼容性,以及二者均需要主动参与响应负荷变化需求。因此,对于故障微电网r,各本地可控DG 单元和应急接入的各MESS均视为一个代理节点共同构成分布式通信网络。此时,相应功率均分控制器同式(14)和式(15),只需将下标X 变为r。 2) SOC 均衡控制 对于故障微电网r中的第m个MESS,还需要在前述功率均分控制器基础上附加SOC 控制。类似地,将表征SOC 的状态量ρr,m代入式(8)和式(9)获取平均SOC 估计值ρ̂r,m,进而得到MESS 的有功功率/SOC 均衡控制器如式(16)所示。随着应急供电过程推移,各MESS 单元SOC 将逐渐趋于一致。 式中:kSr1,m和kSr2,m分别为控制MESS 有功均分及SOC 均衡的积分系数。 考虑到MESS 单元有功功率与SOC 的固有内在联系,对式(16)设计合理的参数kSr1,m、kSr2,m,以提升协同实现有功功率均分和SOC 均衡的动态性能。为此,定义Kr=[kSr1,m,kSr2,m]T,利用线性二次型调节器对参数进行优化设计[28]。 各MESS 单元的动力学模型用状态空间方程表示为: 式 中:Er,m为MESS 单 元 的 能 量;C和D为 状 态 矩阵。若能量基值与MESS 容量相同,则可以用SOC表示MESS 的单位能量。由于本文分别以千瓦时和千瓦作为能量和功率的单位,1/3 600 为对应秒级时间尺度上的转换系数。进一步,给定两个正定矩阵A和B,结合MESS 状态空间方程构造形如式(18)的代数Riccati 方程。 式中:Rr为方程求取得到的唯一正定解。 最终,根据式(18)所求Rr设计得到MESS 单元用于有功功率均分和SOC 均衡的控制参数Kr: 微电网内各DG 及MESS 实际输出角频率跟踪系统额定角频率ω*,当系统达到稳态时实现收敛。由此设计频率二次控制器为: 式中:kωr,i为积分系数。 对于电压恢复控制,为最大限度保障重要负荷的持续运行,故障微电网内关键母线电压Vrc恢复至额定值。对应电压恢复控制器如式(21)所示: 式中:kvr,i为积分系数;gr,i为电源i是否接收关键母线电压额定值信息的状态量,若gr,i=1 表示接收信息,否则表示不接收,故障微电网内有且仅有一个电源能够接收该信息。 定义变量αr,m和βr,m为系统中第m个MESS 的工作状态。其中,当αr,m=0、βr,m=1 时表示MESS需 要接入系统;当αr,m=0、βr,m=0 时表示MESS 已经 接入系统;当αr,m=1、βr,m=0 时表示MESS 需要退出系统。 对于MESS 应急接入系统,以MESS 接入点两侧电压的q轴分量的差值代表相角差:Δθr,mab=Vqma-Vqmb,而幅值差则由两侧电压的d轴分量的差值表示:ΔEr,mab=Vdma-Vdmb。在MESS 接入前,同步接入点两侧电压相角和幅值,减小MESS 接入瞬间对系统的冲击,避免故障进一步扩大。对应的电压相角、幅值预同步控制器分别如式(22)和式(23)所示。 式中:kθr,m和kEr,m为积分系数。 当故障恢复MESS 需要退出系统时,考虑将MESS 出力降低,提前由其余DG 共同承担该部分出力,完成供需功率无缝转移。因此,在实际退出瞬间MESS 出力为零,实现平滑退出。假设共有M个MESS 接入故障微电网,分别设计DG 和MESS 对应的功率转移控制器如式(24)、式(25)和式(26)、式(27)所示。 式中:kΔpr,i、kΔqr,i、kΔpr,m、kΔqr,m为积分系数。 综 上,结 合 式(12)—式(16)及 式(20)—式(27),可得系统中各DG 和MESS 完整的二次控制器分别如式(28)和式(29)所示。 分别将式(28)和式(29)生成的校正项ΩX(r),i、ΦX(r),i和Ωr,m、Φr,m附加于式(1)所示的DG 和MESS的下垂控制方程中,即可实现各项控制目标。 本章在动态收敛算法基础上,结合事件触发思想设计一种全新的通信机制,进一步降低分布式控制器的通信成本和通信压力,以更好地适应系统运行要求,并以优化触发阈值参数为导向,对所提事件触发机制进行收敛性分析。 虽然动态收敛算法性能相较于常规一致性算法大大提升,但相应地也会消耗更多通信资源,这将不利于通信网络临时搭建的故障微电网稳定运行。因此,考虑在控制器中引入事件触发机制,由内置的事件检测模块确定必要的触发时刻ti1,ti2,…,tih,使得各节点仅在触发时刻才执行交互信息操作。对于控制时刻k∈[tih,tih+1],式(10)可改写为: 通信机理可进一步描述为:计算式(30)代入所赋予的触发条件判断,一旦违反触发条件,每个节点将更新并传输其状态;否则,无须信息传递交互,最新触发时刻的状态将保持,直到事件下一次发生。 另外,事件触发机制中设计合理触发条件是保证信息传递准确性的基础。为此,定义基于事件触发的动态收敛算法传输权重信息和状态量信息误差为: 由式(32)可以看出,阈值σi起到触发阈值函数T(σi,x)=σi μ2i的缩放作用,σi取较大的值意味着提高了误差函数H(e)=ζTi→j Ξζi→j下界,即节点i实际状态量与传输给邻居节点状态量偏差累积足够大时才更新控制输入,对应两次通信触发时刻的间隔将增大。同时,也将导致各控制器需要更多迭代计算,以修正节点间较大不平衡量,从而使系统达到全局一致性稳定收敛的时间变长。类似地,若σi取较小的值,则降低了误差函数H(e)下界,本地节点及邻居节点数据采样更新将变得频繁,各控制器需要在迭代计算中修正的不平衡量较小,利于实现系统稳定收敛。因此,需要以优化阈值参数选取为出发点,对所提事件触发机制进行稳定性分析。 假设当触发阈值参数σi满足式(33)时,动态收敛算法的输出将收敛至精确平均值,即 式中:wmin为权重的最小值;zmax和zmin分别为动态状态量的最大和最小值。 接下来,证明触发阈值参数σi满足该上界条件时策略具有收敛性。 定义Li(d)为通信拓扑中最多通过d跳可以到达第i个节点的节点集合,并引入Gi、Gj分别表示断开节点i与节点j通信连接后节点i侧和j侧的节点子集。对于有功和无功功率与其下垂系数乘积γr,i、ηr,i和表征储能SOC 的状态量ρr,m,在以下分析中统一以状态量zi表示。根据式(8)—式(10)和初始化条件,可得第1 次控制时刻节点i向j传递的信息为: 类似地,第2 次控制时刻传递的信息计算为: 以此类推,对于任意k≤di,max,其中,di,max=max {dic|c∈Gi},即节点i与相隔最远的节点间的距离,dic为节点i距离节点c的跳数,则第k次控制时刻传递的信息为: 为了验证本文所提动态协同控制策略的有效性,在MATLAB/Simulink 中搭建含MESS 的微电网群模型进行仿真验证,模型拓扑及对应通信网络结构分别如附录A 图A2 和图A3 所示。系统中,各DG 通过不同的输出阻抗连接到公共电压母线,正常运行时微电网间的联络开关闭合整体互联运行,共同为系统中7 个负载供电。系统中配置3 个MESS 作为应急电源,设置MESS1~MESS3 的初始SOC 分别为77%、73%、69%。在SOC 均衡控制中,由代数Riccati 方程求得的控制参数kSr1,m=-28.284,kSr2,m=7.072,其余仿真参数设置详见附录A 表A1,各负载特征见附录A 表A2。系统故障时,在优先保障重要负荷电能供给的前提下,逐级为一般负载和可中断负载提供电能。 按照本文1.1 节所述4 个阶段对系统整体性能进行仿真测试,系统相应拓扑变换过程如附录A 图A3 所示,仿真时间共25 s。仿真工况设置如下:1)0~1 s 各微电网互联运行,共同为系统负荷供电;2)1 s 时,DG2 故 障 退 出,10 ms 后 系 统 检 测 到 故 障,为保证对尽可能多的负荷供电,系统解列为3 个子微网,同时根据负荷重要程度切除微电网2 内的负载2 和负载4,各移动式储能车前往拟接入位置;3)3 s 时MESS1 启动接入预同步,并于4 s 时接入协同DG3 组网供电,待电压/频率稳定后,5 s 时负载4恢复供电;4)6 s 时MESS2 和MESS3 启动接入预同步,并于7 s 时接入组网供电,SOC 均衡控制启动,同时负载2 恢复供电;5)14 s 时,DG2 故障恢复,重新接入微电网2;6)待系统稳定运行一段时间后,16 s 时各微电网进行同期操作,并于17 s 时重新互联 运 行;7)20 s 时,MESS 启 动 退 出 控 制,将 各MESS 供需功率无缝转移至其余DG,呈现“伪退出”状态;8)22 s 时,各MESS 退出系统。 仿真结果如图4 所示,图中标识线对应上述仿真工况1)~8)。从图中可以看出,初始时刻,微电网群中各DG 有功和无功功率实现精确均分,频率/电压亦稳定在额定值。2 s 时,在DG2 故障瞬间,系统通信网络相应改变,系统出现供需功率不平衡,此时产生较大的频率和电压冲击,待切负荷和解列操作后才重新恢复至额定值稳定运行。在4 s 和7 s时,各MESS 紧急接入系统后,各电源迅速按照容量均匀出力,并且在负荷投入后,各电源迅速调整重新实现功率均分控制。由于各MESS 接入前进行了幅值、相角预先同步控制,在接入瞬间所产生的频率/电压冲击较小。SOC 均衡控制在所有MESS 接入后启动,与有功均分控制器协同实现控制效果,并在13 s 左右各MESS 达到SOC 均衡。14 s 和17 s时,DG2 故障恢复以及各解列微电网合并,系统中各DG 协同MESS 出力,达到新的稳态。20 s 时,各MESS 功率无缝转移,仅产生轻微的频率电压波动,而在22 s 时各MESS 退出系统对系统所造成的冲击几乎为0,实现了平滑退出。 图4 应急控制全过程仿真结果Fig.4 Simulation results of whole process of emergency control 上述仿真算例表明,MESS 接入后立即协同DG 出力,使失电负载迅速恢复供电,且在应急控制的全过程,系统频率/电压仅出现较小波动,始终稳定在额定值,证明了所提控制方法的有效性。 另外,为突出本文所采用控制策略在收敛速度上的优势,分别将其与基于常规一致性算法的控制策略以及文献[20]策略进行对比。仿真工况沿用工 况1)~4),仿 真 时 间 共20 s。如 附 录B 图B1 所示,采用常规一致性算法时,各MESS 最终在19.5 s左右才实现SOC 均衡,对应的DG3 和各MESS 的有功功率实现精确均分。附录B 图B2 展示了采用文献[20]策略的收敛性能。考虑到其收敛速度和暂态性能的权衡性,算法控制参数p和q分别取4/5和5/4,最终各MESS 的SOC 以及各电源有功功率在15.5 s 左右达到均分。同样地,附录B 图B3 展示了相同仿真场景下本文所采用动态收敛算法的性能,仅在13 s 左右便实现了SOC 均衡和有功功率均分,收敛时间相较于常规一致性算法和文献[20]方法分别缩短了6.5 s 和2.5 s。 仿真设置同4.1 节工况1)~4),考虑到应急接入故障微电网的MESS 间以及MESS 与DG 间通信链路为临时搭建,通信环境较差,本节验证通信延时下的控制策略性能。附录B 图B4、图B5 和图B6 分别展示了在100 ms 通信延迟下,常规一致性控制策略、文献[20]控制策略以及本文所提控制策略的仿真结果。对比3 种策略可知,由于常规一致性控制策略和文献[20]控制策略本质上依赖于节点间信息交互的同步性和准确获取,在系统存在较大通信延时环境中会失去稳定。而本文所提策略在较大通信延迟下具有较好的容错性和鲁棒性,系统始终保持稳定且不影响控制器实现相应控制目标,这是由于本文所提控制策略对信息传递的同步性没有严格要求,且策略执行过程中避免了冗余数据,降低了因信息传输延迟或不同步所造成的控制精度下降或系统不稳定的风险。同时,只要通信网络含有生成树,无论拓扑如何,控制策略均是有效的,这对于系统故障后常出现的非理想通信工况展现出更好的适用性。 为了突显本文所设计事件触发机制在经济性方面的优势,在动态收敛算法基础上,分别应用周期触发机制和事件触发机制进行仿真对比测试,仿真工况设置同4.1 节。在周期触发中设置触发间隔为0.01 s,最终仿真得到的有功和无功功率输出及通信间隔如附录B 图B7 所示。而在本文所设计的事件触发机制中,设置系数φ1=φ2=1,所产生的通信间隔如图5 所示。 图5 事件触发机制下的通信触发间隔Fig.5 Communication triggering interval under event-triggered mechanism 对比图4、图5 与附录B 图B7、表B1 可知,本文所提控制策略在两种通信机制下所取得的控制效果几乎一致,达到收敛所需时间在误差允许范围内可认为几乎相同,但相较于周期触发机制,采用事件触发机制时各控制器所发生的触发次数大幅降低,通信间隔显著增大,且不再是等间隔发生通信交互行为,充分体现了本文提出的事件触发机制能够显著降低控制器通信成本。 本文以系统频率/关键母线电压恢复、功率均分以及移动式储能SOC 均衡为目标,提出了一种基于动态收敛算法的微电网群分布式协同控制策略。与传统控制方法相比,具有兼顾收敛性能与通信成本的优势,提高了系统在故障情形下的灵活性与弹性。此外,针对应急电源接入/退出系统易造成的暂态冲击问题,分别在移动式储能接入和退出时引入预同步及供需功率转移策略,以实现其平滑无缝投切。为降低分布式控制器通信成本和通信压力,进一步在动态收敛算法的基础上设计事件触发机制,并给出了以优化触发阈值参数为导向的稳定性分析。通过对含有3 个移动式储能的微电网群系统进行仿真分析,验证了所提控制策略的有效性与优越性。后续可针对控制器时钟偏差导致信息交互不同步的问题展开进一步研究。 本文在撰写过程中受到东南大学“至善青年学者”基金资助,特此感谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。2 故障下微电网群应急协同控制策略
2.1 动态收敛算法
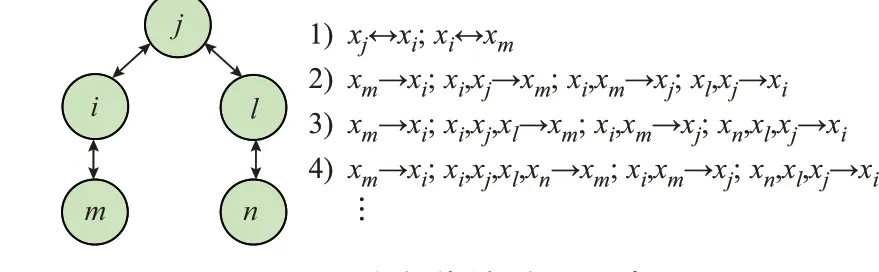
2.2 分布式协同控制器设计
2.3 系统频率/关键母线电压恢复
2.4 移动式储能无缝投切策略
3 事件触发通信机制
3.1 事件触发机理及触发条件


3.2 稳定性分析


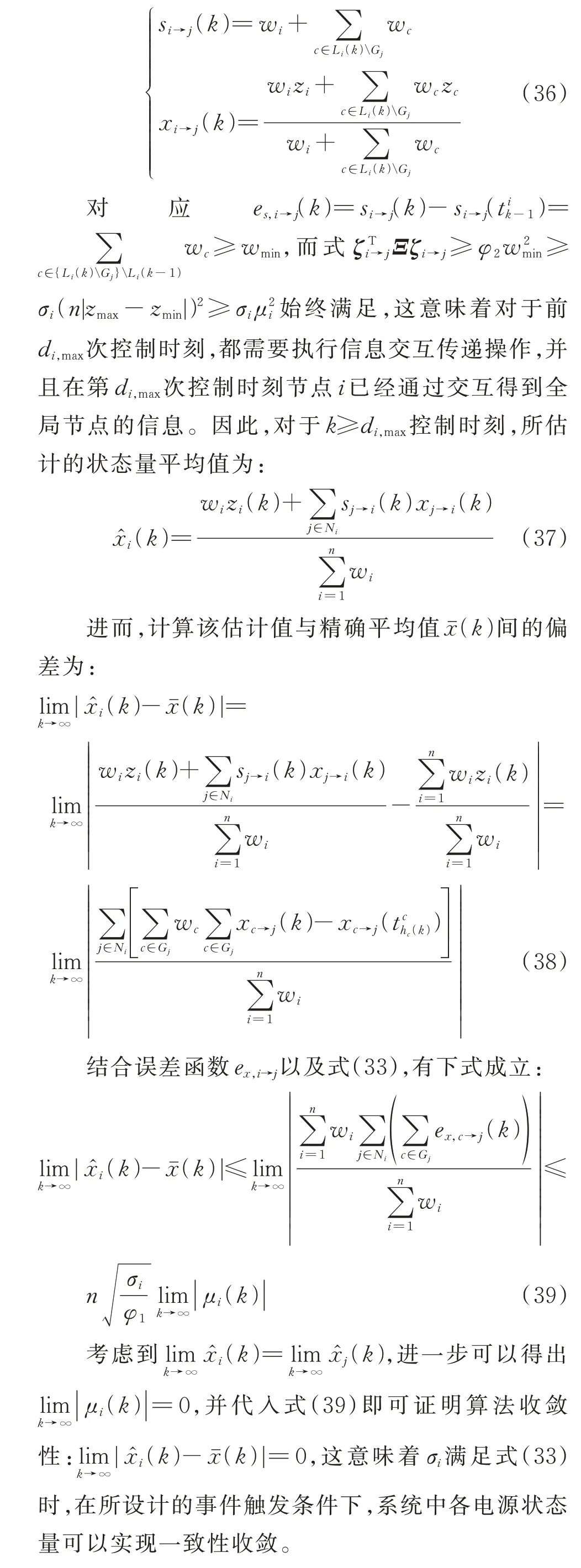
4 仿真验证
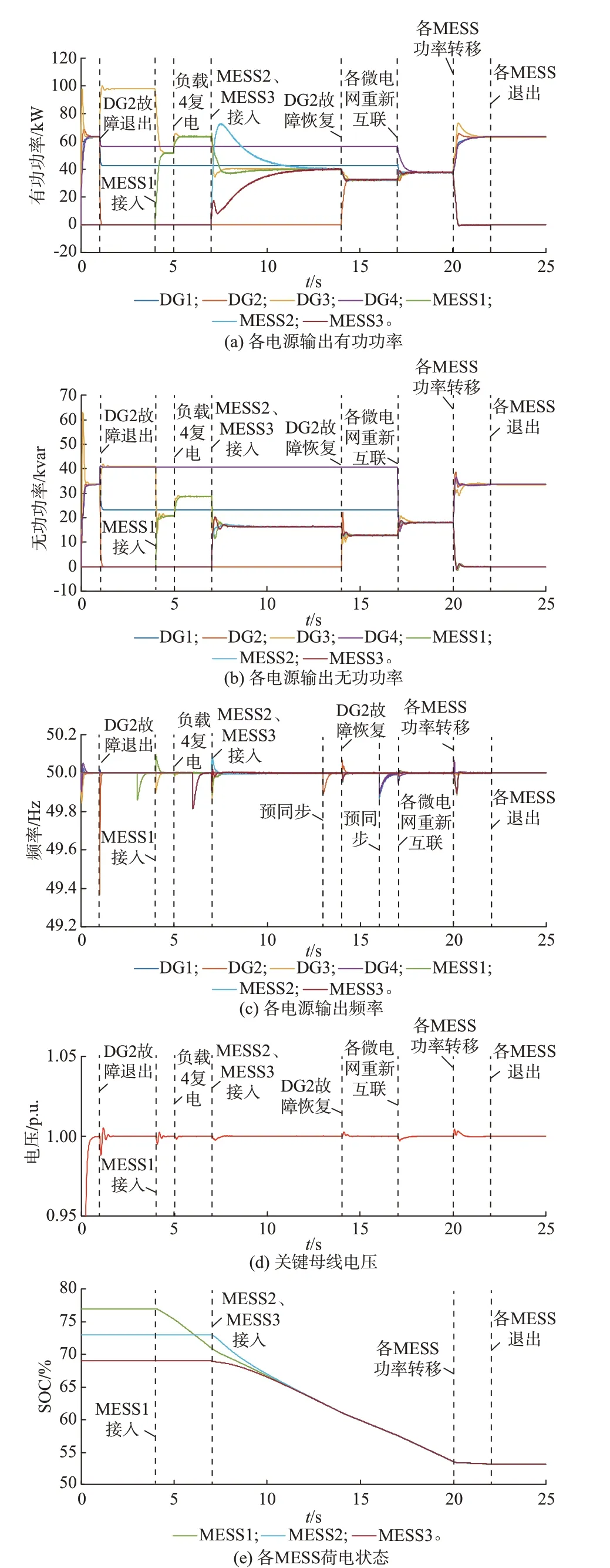
4.1 应急控制有效性验证
4.2 通信延时下的控制性能验证
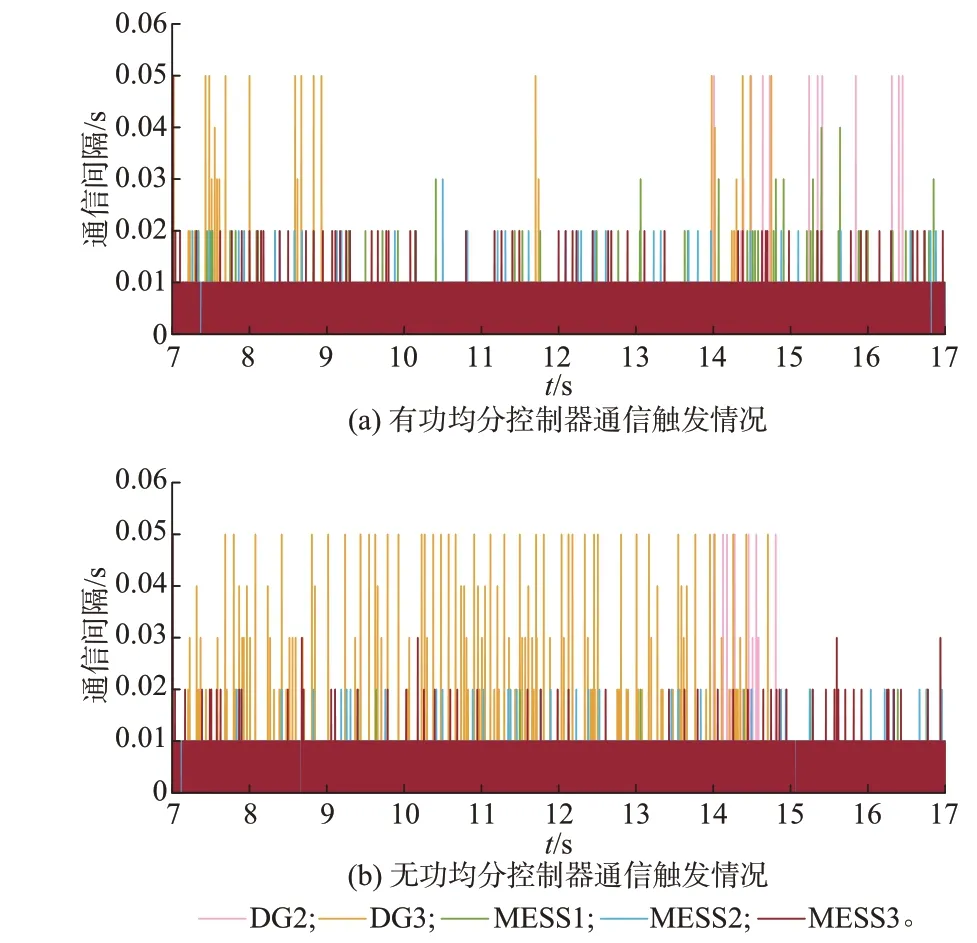
4.3 通信成本对比
5 结语

