计及变压器短期急救负载的城市高压配电网负荷优化分配

王强钢，郭莹霏，莫复雪，周念成，雷 超

（1.输配电装备及系统安全与新技术国家重点实验室（重庆大学）,重庆市 400044；2.国网重庆市电力公司市北供电分公司,重庆市 401147；3.香港理工大学电机电子工程系,香港 999077）

0 引言

城市电网迎峰度夏期间,负荷长时间高位运行,变压器运行风险增加,易导致N-1 故障过载［1］；相邻变压器因短时过载而跳闸退运,进而引发连锁跳闸和系统安全事故。调度中心基于“N-1 安全准则”,削减变压器负荷（一般减至额定容量的40%～60%［2］）以预留安全裕度［3］,导致设备利用率和经济性降低；且紧急故障（如N-1 故障）下,变压器安全与系统安全之间缺乏科学的协同策略［4］。因此,如何挖掘N-1 故障工况下变压器的紧急供电潜力,并结合城市高压配电网负荷转供策略,利用变压器的短时耐受能力支撑系统调控,保障供电可靠性及系统安全稳定运行,在实际工程中具有重要意义。

现有研究利用变电元件热惯性效应探索其短时增容能力［5-10］。文献［11］提出针对风电集群线路N-1 故障为主的输变电元件允许过负荷计算公式,文献［12-13］基于变压器“电-热”耦合关系,延伸变压器热点温度安全极限；文献［14-15］利用有限元法、热电类比法建立变压器温度模型,文献［16］提出一种考虑热点温度与故障率对应的变压器短期增容法。但上述研究均未明确变压器N-1 故障时过载能力边界与环境温度、负载系数变化的准确关系。

城市电网负荷转供有利于提高变压器利用率［17］。目前,中国大中型城市电网涵盖了220 kV/110 kV 高压配电网、35 kV/10 kV 中压配电网和380 V 低压配电网［18］。其中,高压配电网源荷关系、拓扑结构灵活多变,可实现负荷在较大空间尺度上转供；中低压配电网馈线容量小,转供半径较短,难以实现大范围的潮流转移［6］。文献［19］提出变电单元组拓扑表示法,实现高压配电网分组重构。文献［20-22］从线路温升、不同降温措施下主变压器上层油温及多电压等级拓扑三方面更新负荷转供模型的约束。文献［23］提出计及负荷等值阻抗的合环转供分析模型。上述研究仅提高单台变压器运行负载裕度,着眼负荷分配不均/增加引起的自然过载,未考虑多台变压器的协调功率支撑能力及故障过载转供方案。

目前,南瑞集团有限公司在智能电网项目支持下已开展对变压器紧急过载耐受能力的应用研究。本文考虑《电力变压器 第7 部分:油浸式电力变压器负载导则》［24］（以下简称导则）中的短期急救负载,提出一种计及变压器短期急救负载的城市高压配电网负荷优化分配模型,针对主变压器N-1 故障过载工况,构建220 kV 站变压器短期急救负载安全约束下的负荷转供方案。本文核心贡献包括:构建并凸化变压器短期急救负载能力约束,明确变压器故障过载能力边界与负载系数、耐受时间的关系；考虑变压器短期急救负载能力差异,构建站间负荷转供方案,协调利用各220 kV 变压器的短期急救负载裕度。

1 变压器短期急救负载能力约束

当两台变压器并列运行出现N-1 故障时,系统的正常负载分配被干扰,其余正常运行的变压器可能出现严重过载,故障风险增加。由于热惯性效应,在一定耐受时间内,变压器允许出现短时过载［10］。因此,为保证系统安全稳定运行,考虑利用变压器短期急救负载能力重新进行负荷分配,均衡各变压器承载负荷。由导则［24］可知,变压器短期急救负载下的安全运行约束应考虑使用变压器负载量、绕组热点温度和顶层油温不超过其允许值共同表示。同时,本文增加了短期急救负载耐受时间约束,共同构成变压器短期急救负载能力约束。

1.1 变压器平均绕组温度的稳态热平衡方程

根据文献［25］,运用热电类比法,变压器的热传导全过程可简化为等效热路模型［26-27］,如附录A图A1 所示,相关参数解释及变压器各特征点温度之间关系见附录A 第A1 节。

根据文献［28］,变压器的热源为与空载损耗、短路损耗和负荷系数相关的函数,即qt=[P0+(Kt)2Pk]m,其中,qt为变压器绕组热源；P0为空载损耗,Kt为 时 段t的 负 载 系 数；Pk为 短 路 损 耗；m与 变压器绕组层数、油循环速度等因素有关,本文近似取m=1.0［28］。由 附 录A 图A1 可 得 时 段t下 变 压 器 绕组平均温度θtw的状态方程如下:

式中:Cth为变压器内部绝缘油、绕组和油箱等组成的等值热容；Roth为绝缘油侧等值电阻；Rath为散热器向周围空气传热的等效热阻；θta为周围环境温度。

变压器时段t下的绕组热点温度θthst可由变压器绕组平均温度θtw、变压器油箱底层油温θtbo和变压器油箱顶层油温θtto构成的近似公式表示为:

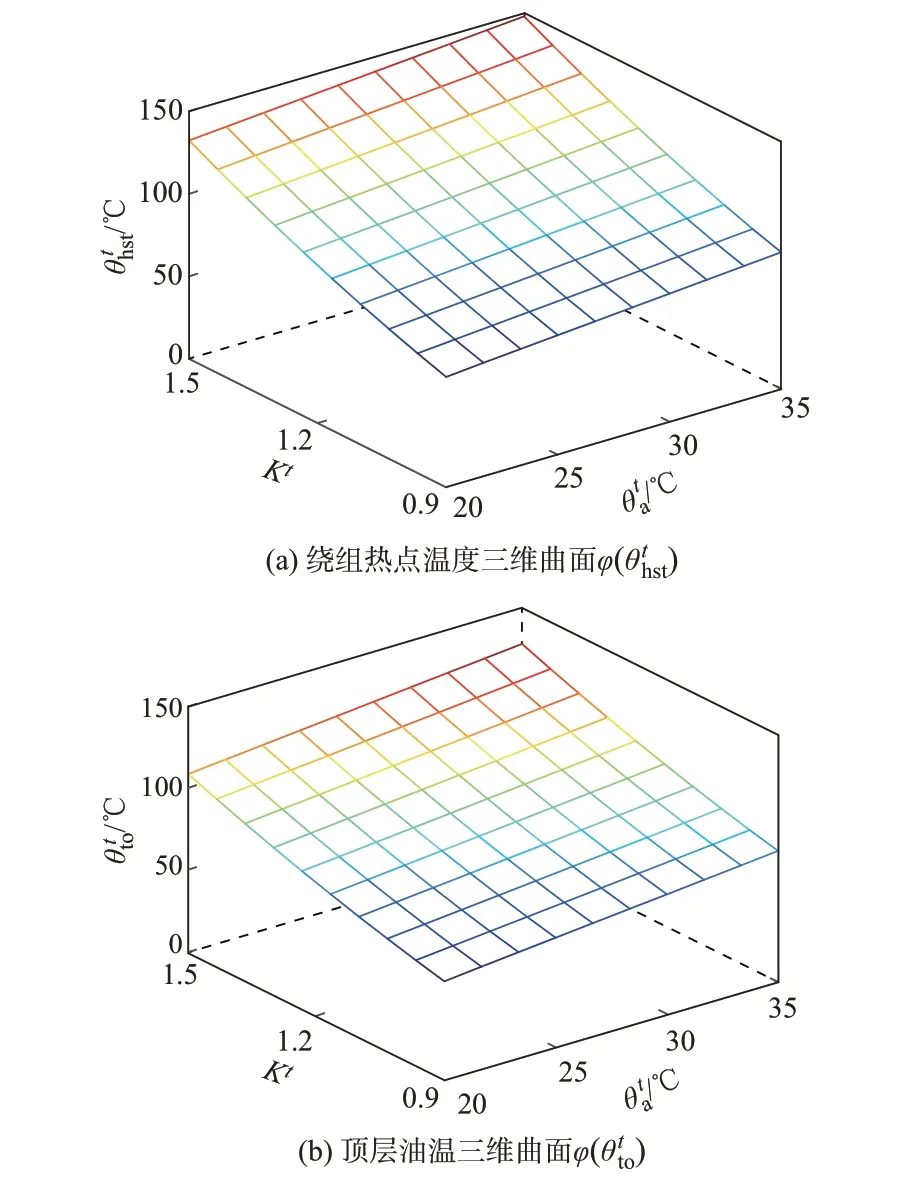
图1 变压器温度与负载系数、环境温度相关的三维曲面Fig.1 Three-dimensional surface of transformer temperature, load factor， and ambient temperature

1.2 变压器短期急救负载能力约束

1.2.1 负载系数、绕组热点温度及顶层油温约束

根据导则［24］,变压器短期急救负载下的安全运行约束包含变压器负载系数约束、绕组热点温度约束和顶层油温约束,如式（3）所示。

1.2.2 耐受时间约束

Δtd、τth与采样周期Δτ之间的关系见附录B 图B1,其为三者取值提供了参考。

1.2.3 变压器短期急救负载能力约束

结合变压器负载系数、绕组热点温度和顶层油温约束式（3）及耐受时间约束式（4）,构成时段t以变压器负载系数Kt及耐受时间Δttts为决策变量的变压器短期急救负载能力约束,如式（5）所示。

1.3 变压器短期急救负载能力约束的凸包转换

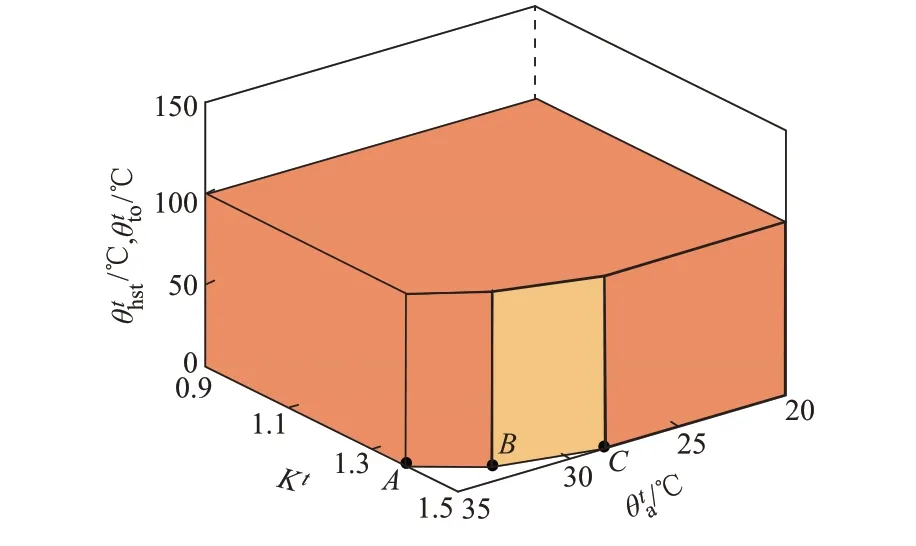
图2 绕组热点温度及顶层油温约束下的等效可行域Fig.2 Equivalent feasible region under constraints of winding hot spot temperature and top oil temperature

为将式（4）对应的非凸可行空间转化为凸约束,本文构造了以三维空间点D′、E′、F′（即D、E、F点在三维图中的对应点）形成的三维平面方程作为其凸包约束,凸包约束平面Θ见附录B 图B4。其中,绿色水平平面为Δttts,max可取的最小值,即一个调度周期时间。结合图3 可知,D′、E′、F′点分别为凸包约束平面Θ可行域范围内的3 个边界点,则该凸包约束平面Θ的方程为:

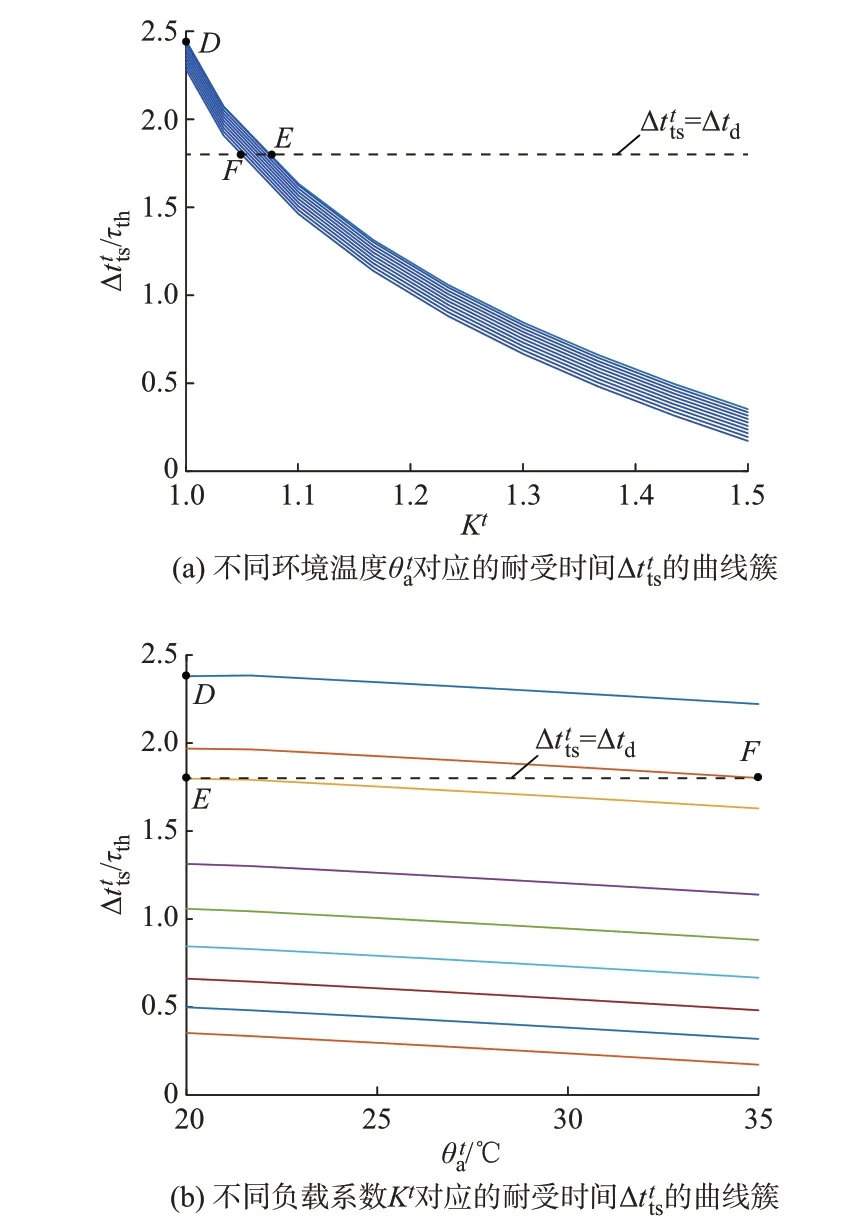
图3 不同变量因子下Δtt ts 的曲线簇Fig.3 Curve clusters of Δtt ts with different variable factors

2 计及变压器短期急救负载的城市高压配电网负荷优化分配模型

当时段t城市电网出现220 kV 变电站N-1 故障紧急工况时,若110 kV 高压配电网内变压器已无剩余负载能力,则只能通过相邻220 kV 变压器过载来分摊转移负荷总量,这可能会导致相邻正常运行的变压器出现轻微过载。过载负荷越大、过载运行时间越长,变压器发生故障的风险将指数级增加。因此,需首先选择不会发生过载的220 kV 变压器来分摊N-1 故障造成的转移负荷总量,同时,避免转供中频繁的开关动作与过多切负荷量。若仍无法解决故障过载问题,则进一步选择过载能力强的220 kV 变压器承担负荷转移任务。由1.2 节可知,Δttts,max较大的变压器在发生过载时,其绕组热点温度和顶层油温上升较慢,具有较强的过载能力,对自身寿命影响较小,在保障设备安全的情况下,可有效提高变压器容量利用率。基于此,需要建立计及变压器短期急救负载的城市高压配电网负荷优化分配模型。

2.1 目标函数

本文以城市电网内运行的220 kV 变压器短期急救负载耐受时间和最长、110 kV 线路开关的操作次数最小［21］、220 kV 变压器过载切负荷量最小［31-32］为优化目标,考虑到实际配电网通常就地平衡无功功率,不涉及网络内输变电设备的传输,本文仅考虑220 kV 变压器有功切负荷量。

消除220 kV 变压器短期急救负载耐受时间和、110 kV 线路开关操作次数与220 kV 变压器有功切负荷量量纲,以标幺值形式表示,将多目标优化问题转为单目标优化问题,目标函数F可表示如下:

2.2 约束条件

基于110 kV 高压配电网典型拓扑结构及负荷转供理论,转供后需满足高压配电网有功平衡［22］、高压配电网典型拓扑［22］、变压器负载系数、开关次数［33］及有功切负荷量约束［34-36］,表示为:

3 求解流程

该模型为混合整数线性规划问题,采用Cplex工具箱进行求解,具体求解步骤如下:

步骤1:获取当前电网各220 kV 变电站可用容量及负荷。

步骤2:获取110 kV 高压配电网拓扑关系,生成各接线方式对应的开关拓扑约束。

4 算例分析

4.1 算例基础数据

在MATLAB R2019b 中,对 附 录C 图C1、图C2 所示的2 个不同规模220 kV/110 kV 实际城市电 网［22］进 行 模 型 验 证。220 kV 变 压 器N-1 故 障当日的环境温度、220 kV 变电站TKJ、XEC、SY、WH、JN、ASQ 站的24 h 负载系数曲线见附录C 图C3。220 kV 变电站TKJ、XEC、SY、WH、JN、ASQ站的变压器热阻参数见附录C 表C1 至表C3。其中,各220 kV 变压器平均绕组温度θtw的初始温度为60 ℃。220 kV 变电站主变压器容量见附录C 表C4。含6 个220 kV 变电站的局部实际城市电网（对应 附 录C 图C1）中Zmax取12［33］,含17 个220 kV 变电站的相对完整实际城市电网（对应附录C 图C2）中Zmax取20［37］。

4.2 单个220 kV 站N-1 过载的转供优化结果分析

4.2.1 TKJ 站N-1 故障后转供优化方案及结果

H社区的资金受到区政府限制，并且资金的审批过程复杂，时间长，效率低，导致许多老旧小区的消防安全设施无法得到有效完善，存在一定的安全隐患，对居民的人身安全具有潜在的威胁。

为验证本文所提转供优化计算完备性,SY 站、XEC 站发生N-1 故障时的转供优化方案见附录D表D1 和表D2,本节仅分析TKJ 站N-1 故障后的转供优化方案及结果。由附录C 图C3 可知,11:30时θta=31.6 ℃,220 kV 的TKJ 站出现变压器N-1故障的紧急工况,其负载系数瞬间达到1.4,此时启动本文所提计及220 kV 变压器短期急救负载的转供优化计算,得到开关动作方案如附录D 图D1所示。

表1 给出TKJ 站N-1 故障工况下负荷转供前后各相关220 kV 站负载系数变化以及过载耐受时间。由表1 可知,通过执行附录D 图D1 的转供优化开关动作方案,将220 kV 的TKJ 站过载负荷转移至其他220 kV 变电站,其负载系数从1.400 下降至0.984。其中,WH 站、ASQ 站、XEC 站、TKJ 站均没有出现过载,而JN 站轻微过载。JN 站变压器短期急救负载耐受时间为109.44 min,远远大于转供优化的调度周期15 min 及转供前TKJ 站的短期急救负载耐受时间24.85 min。这表明本文所提计及220 kV 变压器短期急救负载的转供优化工具能够选择当前状态下短期急救负载能力更强的变电站分担已过载变电站的过负荷,进一步挖掘JN 站变压器的短时过载能力来缓解TKJ 站变压器N-1 故障后的故障过载紧急工况。

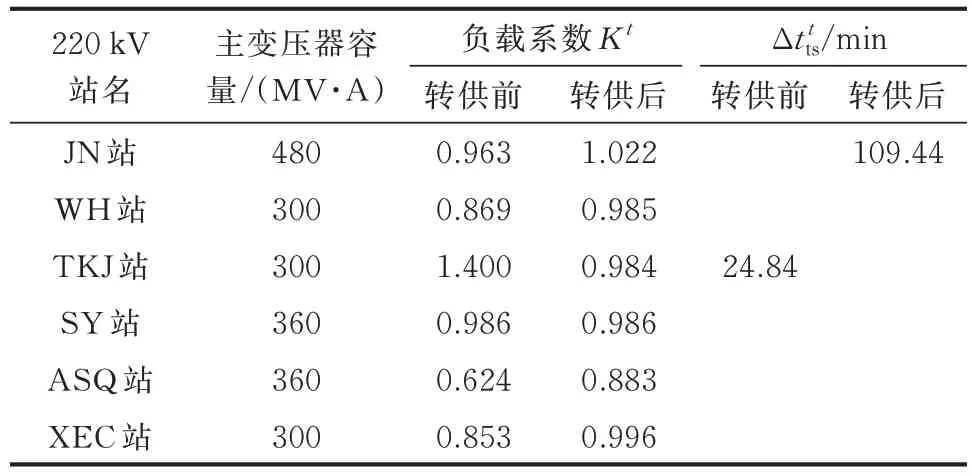
表1 TKJ 站N-1 故障工况下转供前后220 kV 站负载系数及过载耐受时间Table 1 Load coefficient and overload tolerance time of 220 kV station before and after power supply transfer under N-1 fault condition of TKJ station

4.2.2 单站N-1 过载转供前后的电网允许过载变电容量对比

为衡量城市电网当前状态下的整体短时过载耐受能力,本节在忽略电网拓扑变化的前提下,建立电网允许过载变电容量（permissible overload variable capacity of power grid,POVCOPG）指标SP:

式（12）以变压器有功负荷对相应时段短期急救负载耐受时间积分,并在220 kV/110 kV 城市电网内对所有220 kV 变压器求和的形式计算电网允许过载变电容量指标。SP值越大,电网允许过载变电容量越大,电网的整体短时过载耐受能力越强。

针对220 kV 变电站TKJ、SY、XEC 站主变压器发生N-1 故障工况的3 种场景,对比转供前后电网允许过载变电容量SP变化,如图4 所示。

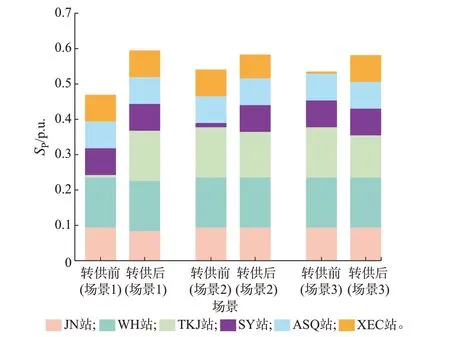
图4 各变电站N-1 故障时转供前后SP 对比Fig.4 Comparison of SP before and after power supply transfer when N-1 fault occurs in each substation

由图4 可知,TKJ、SY、XEC 站变压器N-1 故障场景下（即场景1～3）,负荷转供后该220 kV/110 kV 城市电网的电网允许过载变电容量均大于负荷转供前的电网允许过载变电容量,验证了本文模型可有效扩增电网允许过载变电容量并提升220 kV/110 kV 电网整体短时过载耐受能力。

另外,本文探究了所提模型在多个220 kV 站过载场景下的有效性,算例结果及分析见附录D。

4.3 不同转供模型对比及凸包转化精确度分析

为测试本文所提变压器短期急救负载下的约束及所用凸包方法对转供优化方案的影响,对3 种模型在相对完整的实际城市电网中,220 kV 的TKJ站及XEC 站过载工况下的转供优化结果进行对比分析,如表2 所示。

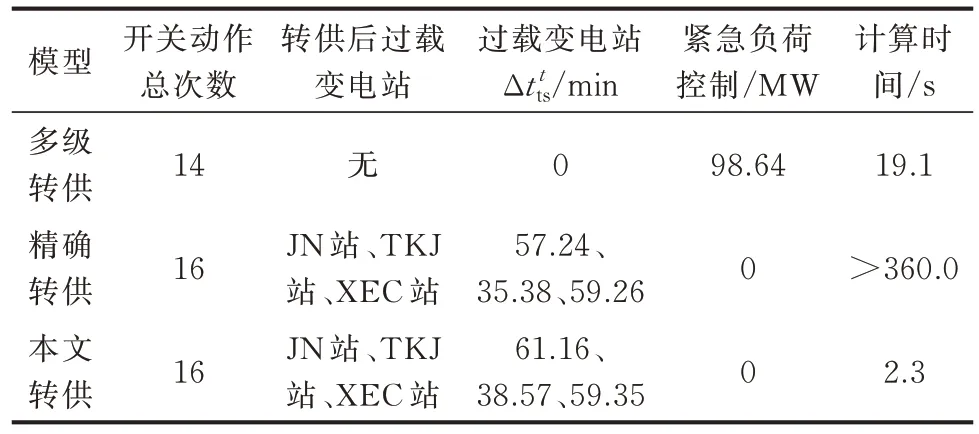
表2 多站过载时不同模型的转供结果对比Table 2 Comparison of power supply transfer results of different models under multi-station overload

表2 中,多级转供模型［22］为不考虑变压器短期急救负载耐受时间的多级电压协调转供模型,采用Cplex 进行求解；精确转供模型基于变压器短时过载耐受时间非线性的特性（对应式（5））,为考虑变压器短期急救负载耐受时间的非线性优化转供模型,采用遗传算法进行求解；本文转供模型为在精确转供模型基础上对非线性约束集进行凸包转化（对应式（8））的考虑变压器短期急救负载耐受时间的线性转供模型。

由表2 可知,多级转供模型因配电容量约束,在转供优化结束后所有变电站均不过载,但需进行切负荷。精确转供模型及本文转供模型由于不进行紧急负荷控制,需要将全部过载负荷分散至不同变电站内变压器。因此,开关动作总次数更多。这表明,本文模型在确保设备安全的同时能不拉限负荷,保障了用户持续供电需求,转供负荷范围更广。

对比精确转供模型与本文转供模型可知,在过载变电站选择及开关动作总次数上二者相同,过载变电站短时过载耐受时间由于凸包转换呈现一定误差,但仍在可接受范围内,验证了本文所提转供优化模型的合理性及有效性。另外,本文转供模型由于在精确转供模型基础上进行凸包转化,其计算时间为2.3 s,小于多级转供模型计算时间（19.1 s）,远小于精确转供模型计算时间（>360 s）。由此可见,将约束凸包转化以数量级为单位提升了模型计算效率,为城市电网中实时转供优化计算奠定了基础。

此外,由于凸包约束对原约束进行了转化,以下详细对11:30 时TKJ 站变压器的Δttts凸包方程进行转供优化求解时的精确度进行分析。图5 给出了TKJ 站变压器按照N-1 故障计算形成过载Kt曲线后,非凸方程Δttts,max的凸包平面方程Θ及其与非凸曲面φ(Δttts,max)之间的三维误差分布。

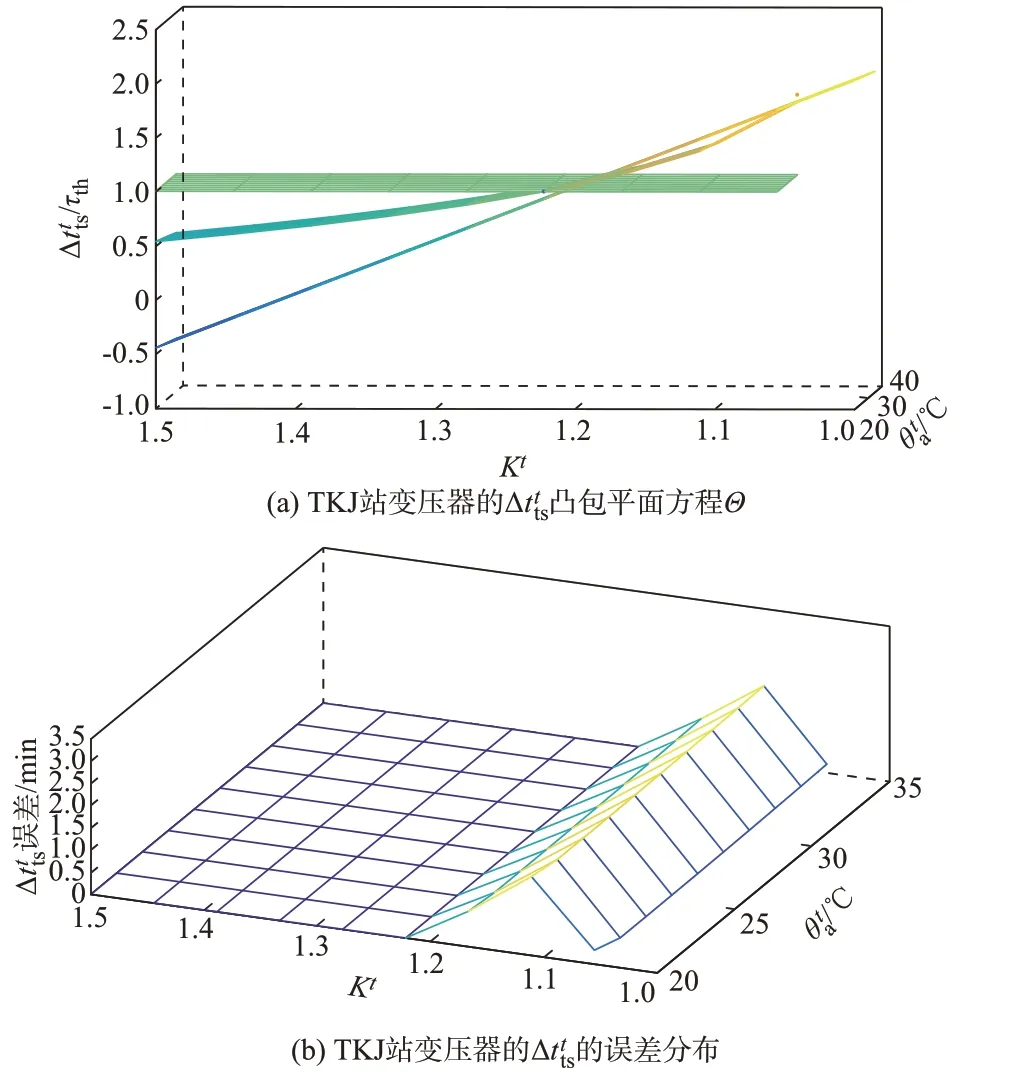
图5 TKJ 站变压器的Δtt ts 凸包平面方程Θ 及误差分布Fig.5 Δtt ts convex hull plane equation Θ and error distribution of transformer in TKJ station

综上所述,充分利用负荷转供优化策略及220 kV 变压器N-1 故障过载紧急工况下的短期急救负载能力,能够有效提升变压器N-1 故障工况时的电网负荷转移响应能力,提高电网运行限额,为解决“网-荷”协调不同步问题提供解决方案；有效替代传统的负荷拉限方式,尽可能保障用户的持续可靠供电,提高电网运行的安全可靠性。通过运用110 kV 高压配电网的负荷转供与220 kV 变压器短期急救负载能力相结合的方法,将进一步挖掘出220 kV 变压器的潜在剩余供电容量,提升220 kV 变压器安全运行的载流量边界,有效提升城市电网在变压器N-1 故障过载工况下的供电能力。

5 结语

在城市电网变压器容量利用率低、预留安全裕度大、易退运导致系统供电可靠性低的背景下,本文针对变压器N-1 故障过载,提出一种计及变压器短期急救负载的城市高压配电网转供优化策略,具有以下特点:

1）考虑变压器短期急救负载耐受时间对其短期急救负载能力的影响,构建变压器短期急救负载能力非凸约束并进行凸化,明确变压器短时过载能力边界与负载系数、耐受时间的关系；

2）负荷转供中选择短期急救负载能力强的变压器分摊过负荷,保障有功切负荷量、开关操作次数最小,提升电网整体短时过载耐受能力,均衡城市电网各220 kV 站负载水平；

3）使用凸包算法,在保证精度的前提下提升计算效率,为实时转供计算奠定基础。

所提策略为220 kV 变压器故障过载以致设备损坏、用户大面积停电等问题提供了解决思路,保障城市电网持续可靠运行,也对缓解输配电阻塞、提高电网运行限额具有参考价值。

随着高比例分布式能源并网运行,其出力的间歇性、波动性势必对配电网拓扑结构、潮流水平产生影响。本文策略仅考虑高压配电网的负荷转供策略,未考虑其他输配电设备故障对负荷转供的影响,具有一定局限性。后续将研究高比例分布式电源并网后对中低压配电网负荷优化分配方法的影响,并考虑多种分布式电源出力及配电网负荷转供路径优化,研究计及分布式电源和多电压等级配电网的精细化负荷优化分配方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。