考虑配电网电压约束的光伏功率升维仿射控制
施路炜,徐潇源,严 正,陆建宇
(1.电力传输与功率变换控制教育部重点实验室(上海交通大学),上海市 200240;2.上海非碳基能源转换与利用研究院,上海市 200240;3.国家电网有限公司华东分部,上海市 200120)
0 引言
近年来,对于可再生能源的研究利用得到了广泛关注。在政策的大力支持下,配电网中光伏电源数量日益增长,提升了清洁能源在配电网中的占比,有助于减少碳排放,实现“双碳”目标。但光伏发电出力的随机波动特性对系统运行带来了不确定性,并引发节点电压越限等问题[1-4],造成了光伏消纳难题。其中,环境因素的改变导致光伏出力短期预测难度增大,给配电网运行控制带来不确定性,亟需可靠的应对策略。
光伏可通过逆变器对输出的有功功率进行削减或调节无功功率来参与电网调压[5]。配电网中光伏控制方式分为集中式、分布式以及就地式等[6]。集中式控制需要全局通信且控制周期长,对功率、电压波动响应速度慢;分布式控制中各控制节点与相邻节点通信以实现预设控制目标,相比于集中控制降低了通信与计算负担,但是可能存在算法收敛性问题;就地控制仅收集本地量测信息,能快速响应功率、电压波动,但是传统就地控制缺乏系统层面的协调。本文研究范畴为光伏就地控制。
光伏就地控制策略包含有功功率-电压(P-V)下垂控制[7-8]、无功功率-电压(Q-V)下垂控制[9-12]以及无功功率-有功功率(Q-P)控制[13-14]等。文献[15]在最优潮流中加入P-V下垂控制模型进行优化,在抑制过电压的同时减少光伏的出力削减。文献[16]基于电压-有功灵敏度系数矩阵计算P-V下垂控制斜率,在抑制过电压的同时实现有功削减量在不同光伏之间的合理分配。文献[17]的Q-V就地下垂控制在抑制过电压的同时,能兼顾网损减小、无功消耗降低、光伏间无功功率合理分配等目的。文献[18]提出了考虑平抑电压波动的Q-V控制曲线斜率计算方法。文献[19]基于电压-无功灵敏度系数矩阵和电压越限边界点确定Q-V下垂控制斜率范围,并以网损最小为目标优化控制曲线。文献[20]结合P-V与Q-V下垂控制以抑制过电压。P-V与Q-V下垂控制能够有效解决光伏接入引发的电压波动和越限问题,但是难以考虑电压安全约束以明确所容许的有功与无功功率范围。
针对Q-P控制,文献[21]基于历史数据生成分段式的就地Q-P控制曲线以实现更精确的电压控制。文献[22]采用不确定性集合刻画光伏有功功率波动范围,引入仿射控制策略将光伏无功功率作为依赖于有功功率的函数进行调节,通过求解以系统网损、电压偏差最小为目标的集中优化问题,获得Q-P就地控制策略。文献[23-24]将电压控制问题解耦为若干子问题,利用交替方向乘子法进行分布式求解,得到光伏Q-P仿射控制策略。文献[25]提出了光伏功率的准许区间(admissible range)概念,在传统Q-P控制策略基础上实现有功削减的功能:当光伏有功功率在准许区间内时进行Q-P控制,当光伏有功功率在准许区间外时则进行弃光,以满足配电网电压安全约束;通过优化Q-P控制策略来扩大准确区间范围、降低有功削减。但是上述研究没有考虑配电网的三相模型,并且Q-P控制策略为线性函数,限制了光伏功率的安全波动范围。
本文针对含光伏的三相配电网,构建了电压约束下适用于光伏就地控制的功率安全波动区间,提出了光伏功率升维仿射控制方法,灵活协调光伏逆变器的有功-无功功率控制,能够在保证电压安全约束的前提下提升配电网的光伏消纳能力。首先,对于三相配电网LinDistFlow 中的节点电压计算公式,提出了考虑电压调节器(voltage regulator,VR)的修正模型。其次,基于修正后的电压计算公式与仿射控制策略,构建最大化光伏功率安全波动区间的优化问题。然后,引入空间升维的分段线性化仿射控制方法,以避免传统分段线性化中引入的整数变量,并基于二进制展开(binary expansion,BE)、对偶理论等构建了优化问题的求解方法。通过求解上述模型得到配电网中各光伏的功率安全波动区间以及对应的分段线性控制策略。最后,采用IEEE 123节点三相配电网进行仿真分析,并通过与线性仿射控制策略进行对比,验证所提方法在提高配电网光伏消纳能力、保证节点电压安全方面的作用。
1 三相配电网电压计算公式
1.1 基于三相配电网LinDistFlow 的电压公式
三相配电网中常用的线性潮流模型LinDistFlow[26-30]考虑了三相对称情况下线路相间阻抗的耦合,可表示如下:
式 中:i→j表 示 潮 流 由 节 点i流 向 节 点j;Sij,ϕ为 节 点i流 向 节 点j的ϕ相 功 率;Sij为 节 点i流 向 节 点j的 三相功率构成的列向量;sj,ϕ为节点j的ϕ相注入功率;N为节点集合;N+为加上馈线首端节点的节点集合;上标“*”表示矩阵或向量中的元素取共轭;Zij为节 点i至 节 点j的 线 路 三 相 阻 抗 矩 阵;Z͂ij为 节 点i至节点j的线路三相等效阻抗矩阵;η=[1,η,η2]T,其中,η=e-j(2π/3);Uref0为馈线首端节点三相电压列向量;V0为馈线首端节点三相电压模值平方列向量;Ui为节点i的三相电压列向量;Vi为节点i的三相电压模值平方列向量;上标“H”表示转置共轭。式(1)为配电网节点功率平衡方程;式(2)表示线路潮流导致的电压降落;式(3)为三相电压平衡假设下的线路等效阻抗矩阵计算公式。

式中:p和q分别为节点注入有功、无功功率的列向量;R和X为电压灵敏度矩阵;|N|为集合N中元素总数;blkdiag(∙)表示求分块对角矩阵;Z͂i为流向节点i的线路三相阻抗矩阵经η作用后的结果,计算方式同式(3);F=-A-1bus,其中,Abus为降阶的支路母线关联矩阵;ei为单位矩阵I|N|的第i列;⊗为Kronecker 张量积运算符。
1.2 计及电压调节器的修正公式
当系统中有电压调节器时,需要对上述电压灵敏度矩阵R、X进行修正。设配电网中电压调节器的变比为kr,ϕ,可得:
式中:Vπr为节点r上游节点的三相电压模值平方向量;Vr为节点r三相电压模值平方向量;Sr为流向节点r线路的三相功率构成的列向量。
由此可知,变比会影响下游节点的电压和电压灵敏度矩阵。可利用矩阵F=-A-1bus识别下游线路:矩阵F的第r列记录了节点r(按照生成支路母线关联矩阵的命名规则,线路r总是流入节点r)的下游线路的信息,第r列中第j行元素为1 表示线路j是节点r的下游线路。
因此,考虑电压调节器的修正公式为:

式中:CrV为列向量,满足CrV⊙CV=[1,1,…,1]T;R͂和X͂为修正后的电压灵敏度矩阵;V͂0为修正后馈线首端节点电压列向量,其规模为3|N|×1;Vref、pref、qref分别为节点电压和注入有功、无功功率的基准值;ΔV、Δp、Δq分别为节点电压和注入有功、无功功率的变化量。
2 光伏功率安全波动区间优化
2.1 光伏功率安全波动区间定义
采用区间型不确定性集合表示光伏的不确定性如下:

为满足就地控制时光伏间相互解耦的特性,不确定性建模无法考虑变量间的相关性,存在结果过于保守的问题,但本文采用集中优化求解就地控制策略,具有全局优化效果,一定程度上缓解了保守性。由于精确预测、刻画光伏出力在短时间尺度上的不确定性难度较高,参考新能源调度波动限额(do-not-exceed,DNE)概念[31-32],在区间型不确定性集合基础上定义配电网安全运行约束下光伏出力最大波动范围如下:
定义1:光伏功率安全波动区间指对于配电网中的每个光伏而言,存在有功出力的安全区间,使得该光伏的有功出力在该区间内任意波动时能保证配电网任意节点电压都不越限。该区间包含于光伏功率不确定性范围之内,为光伏就地控制提供有功功率的安全边界。
安全波动区间上、下界满足:

在应用中,配电网每经过时间间隔Δt(根据实际情况选择,一般为15 min~1 h),采用预测的光伏出力及系统负荷重新计算并更新光伏功率安全波动区间,并将之发送到每个光伏节点作为就地控制的边界约束。
2.2 优化问题建模
2.2.1 目标函数
为在电压安全约束下提高光伏消纳范围,设置优化问题目标函数为光伏功率安全波动区间范围之和最大:
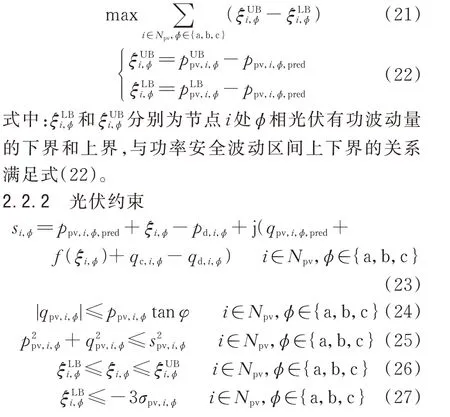
式 中:pd,i,ϕ为 节 点i处ϕ相 负 荷 的 有 功 功 率;qpv,i,ϕ,pred为节点i处ϕ相光伏的无功功率固定值;f(ξi,ϕ)为节点i处ϕ相光伏的无功功率波动量,是关于ξi,ϕ的仿射 函 数;qc,i,ϕ为 节 点i处ϕ相 的 并 联 电 容 容 量;qd,i,ϕ为节点i处ϕ相的负荷无功功率;ppv,i,ϕ=ppv,i,ϕ,pred+ξi,ϕ为 节 点i处ϕ相 光 伏 的 实 际 有 功 功 率;qpv,i,ϕ=qpv,i,ϕ,pred+f(ξi,ϕ)为节点i处ϕ相光伏的实际无功功率;φ为功率因数角上限;spv,i,ϕ为节点i处ϕ相光伏容量;σpv,i,ϕ为节点i处ϕ相光伏有功功率的标准差。式(23)为节点注入功率;式(24)为光伏功率因数约束;式(25)为光伏逆变器容量约束;式(26)为光伏有功功率随机波动量的安全波动区间约束;式(27)保证光伏的有功功率安全波动区间下界ξLBi,ϕ小于 光伏的实际有功出力,防止光伏出力小于安全波动区间下界而导致切负荷。本文采用3σ原则限定安全波动区间下界的最大值。若采用概率预测技术获得预测区间下界,则可以更准确地设定安全波动区间。
2.2.3 电压约束
节点电压的约束为:

3 基于升维分段线性仿射控制的优化模型

3.1 变范围约束的转换

3.2 光伏有功-无功升维分段线性仿射控制策略
对于光伏的Q-P控制,建立升维分段线性仿射控制关系[33-34]。考虑到光伏有功出力增加或减少时,逆变器Q-P平面中可行域有较大区别,因此,将控制曲线分为两段,分别实行不同斜率的仿射控制策略。
对于0 ≤γi,ϕ≤1,设分段点为zi,ϕ=0.5,则可将变量从一维空间升至二维空间:
式 中:Y′1和Y′2分 别 为Y′i,ϕ,1和Y′i,ϕ,2作 为 对 角 元 构 成的对角矩阵。
式(34)所定义的变量定义域如图1 中红色折线所示,该定义域非凸。为方便控制问题求解,将定义域扩展为其凸包,即其所有顶点为极点构成的凸集,如式(39)所示。凸包的几何表示如图1 中三角形区域所示[34]。
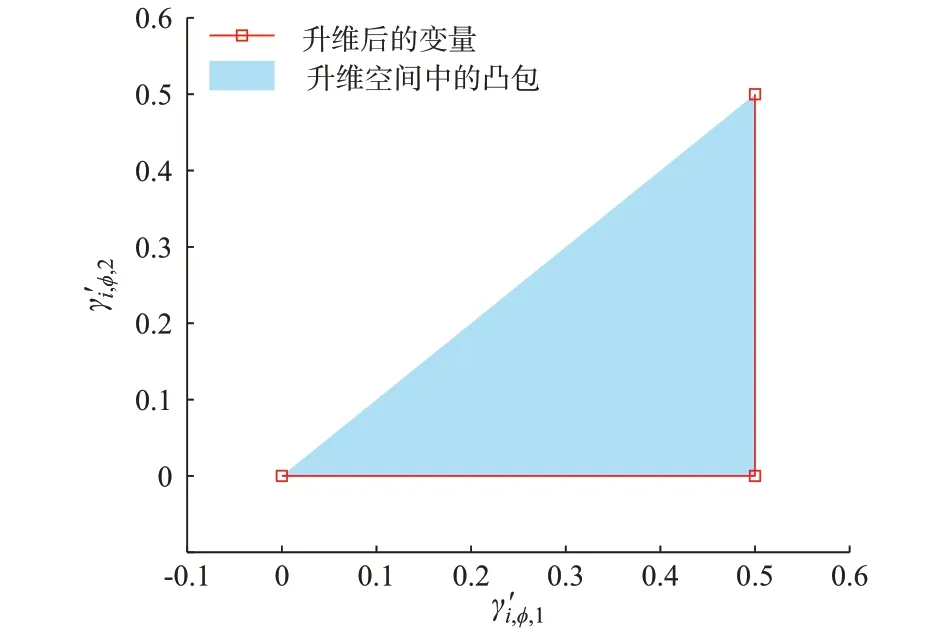
图1 升维后的变量及其凸包示意图Fig.1 Schematic diagram of dimension-lifting variable and its convex hull
其中,
通过空间升维,能够避免传统分段线性方法引入的整数变量及相关约束,以更小的计算代价实现分段线性控制策略,同时,可以对鲁棒约束进行等价转化。具体说明见附录A。
3.3 鲁棒约束转换
将式(36)和式(38)代入式(29),可得:


对于此类存在0-1 变量与连续变量相乘的混合整数优化问题,可以采用大M法进行转化,也可以采用求解器直接求解,此处不再赘述。
4 算例分析
4.1 IEEE 123 节点三相配电网模型
IEEE 123 节点三相配电网的拓扑如图2 所示。由于IEEE 123 节点系统的节点编号方式不利于降阶支路母线关联矩阵的计算以及后续建模,对其进行节点重命名,重命名前后的节点对照表见附录C表C1。光伏信息如表1 所示,光伏接入节点编号为原始节点编号。
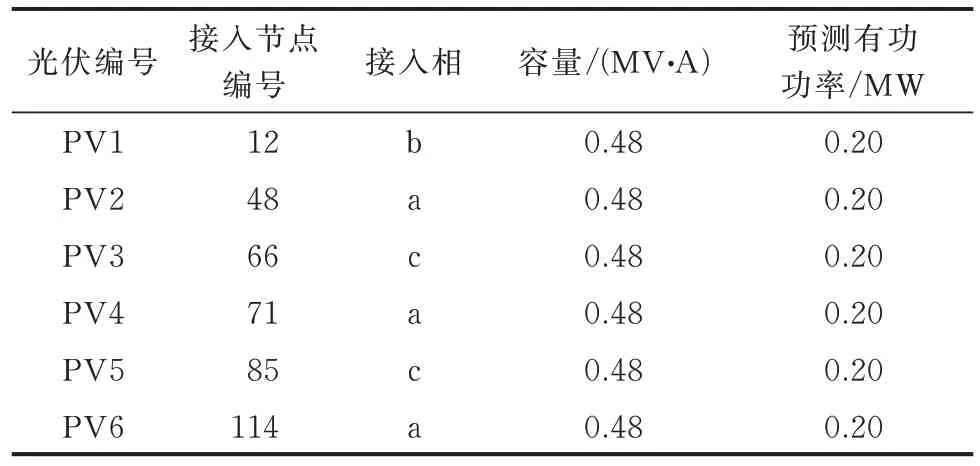
表1 光伏详细信息Table 1 Detailed information of photovoltaic
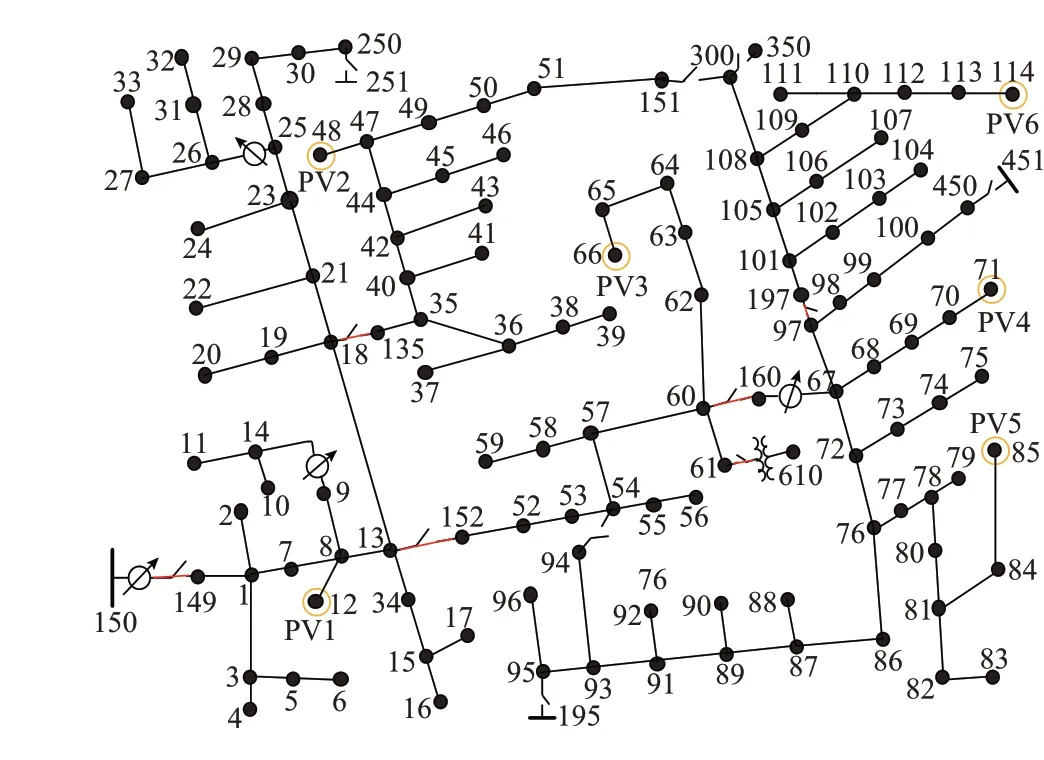
图2 带光伏的IEEE 123 节点配电网拓扑Fig.2 Topology of IEEE 123-bus distribution network with photovoltaic
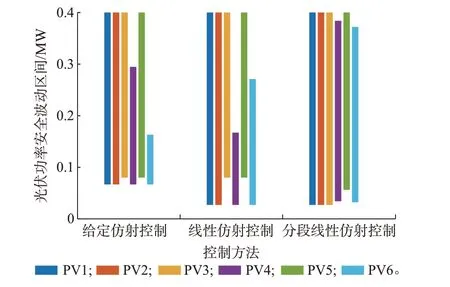
图3 光伏功率安全波动区间Fig.3 Safe fluctuation interval of photovoltaic power
IEEE 123 节点三相配电网的负荷情况如下:有功功率为3.62 MW,无功功率为1.32 Mvar,视在功率为3.86 MV∙A。系统中接入的光伏总容量为2.88 MV∙A,约占系统总负荷的74.6%,为具有高光伏渗透率的配电网。在光伏接入节点选择上,保证了首末端(距离馈线首端节点远近)均有光伏接入;在接入相的选择上,三相均有光伏接入,且相与相间存在一定的不平衡。
4.2 电压修正公式准确性验证
为验证电压修正式(17)的计算准确性,对IEEE 123 节点三相配电网分别利用电压计算修正前的式(6)和修正后的式(17)进行电压求解,将计及电压调节器变比的三相线性配电网潮流模型作为比较基准,修正前后电压计算结果对比如附录D 图D1所示。未修正的电压计算结果相对误差较大,表明非标准变比电压调节器对配电网电压有较大影响;修正后的电压计算结果与基准基本一致,验证了考虑电压调节器的修正公式的计算准确性。
4.3 光伏功率安全波动区间
将所提出的升维分段线性仿射控制与给定仿射控制、线性仿射控制等方法进行比较。给定仿射控制模型较为简单,不再单独给出推导;线性仿射控制优化模型推导过程见附录E。
1)给定仿射控制:仿射控制系数设置为Yi,ϕ=-0.1。

从PV1 到PV6,距离线路首端越来越远。处于线路末端的光伏,其功率波动对电压的影响相对处于线路首端的光伏更大,因而,处于线路首端的光伏易于获得更大的安全波动区间,处于线路末端的光伏功率安全波动区间较小,首末端光伏的波动区间分配存在一定的不公平性。
4.4 光伏功率控制策略
1)给定仿射控制
附录D 图D2 为给定仿射控制示意图,仿射规则曲线的左右边界为光伏有功出力物理极限,分别为0 MW 和0.4 MW。给定仿射控制曲线及下文两种方法的控制曲线均能够满足光伏的容量约束(绿色虚线)以及功率因数约束(蓝色虚线)。
2)线性仿射控制
附录D 图D3 展示了光伏线性控制曲线及其安全波动区间、预测出力、逆变器容量、功率因数约束。光伏就地控制依据安全波动区间中的线性控制曲线,对光伏出力超过区间上界的部分进行“弃光”;而本文按照3σ原则设定安全区间下界。因此,光伏出力小于区间下界的概率极小,其影响可以忽略。仿射系数通过求解优化问题得到,而非给定数值。因此,线性仿射控制下光伏功率安全波动区间不会小于给定仿射控制所得区间。
3)升维分段线性仿射控制
升维分段线性仿射控制曲线以及对应的安全波动区间1 和2、预测出力点、逆变器容量约束、功率因数约束如图4 所示。光伏就地控制依据安全波动区间1 和2 中的分段线性控制曲线,有功功率超出上下界的处理方式与线性仿射控制相同。各段仿射系数范围包含了线性仿射控制的情况。因此,升维分段线性仿射控制下的安全波动区间不会小于线性仿射控制所得区间,进一步减少了弃光场景。
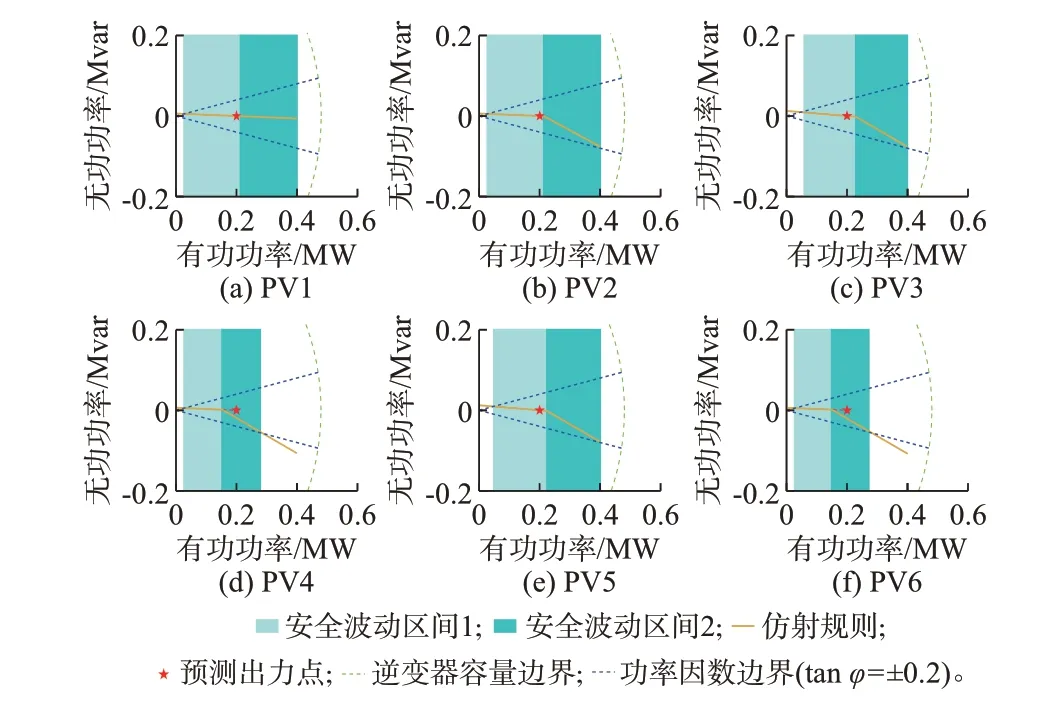
图4 升维分段线性仿射控制曲线Fig.4 Curves of dimension-lifting segmetation linear affine control
值得注意的是,仿射控制曲线并不总是经过预测出力点,按照第3 章中建立的分段线性仿射规则式(38),仅当预测出力点在光伏安全波动区间1 时,曲线经过预测出力点;当预测出力点在光伏安全波动区间2 时,预测出力点位于仿射控制曲线第1 段的延长线上。
4.5 光伏消纳量分析
为验证所提出的仿射控制策略对提高配电网光伏消纳的作用,对光伏消纳量进行50 次蒙特卡洛模拟。模拟方式为:光伏的有功功率是以光伏预测有功 功 率ppv,i,ϕ,pred为 期 望、σpv,i,ϕ为 标 准 差 的 正 态 分 布,并满足5σpv,i,ϕ=ppv,i,ϕ,pred。图5 表明,采用升维分段线性仿射控制时光伏消纳总量均优于其余两种情况,模拟场景中至多提升22.28%,有效减少弃光现象的发生。
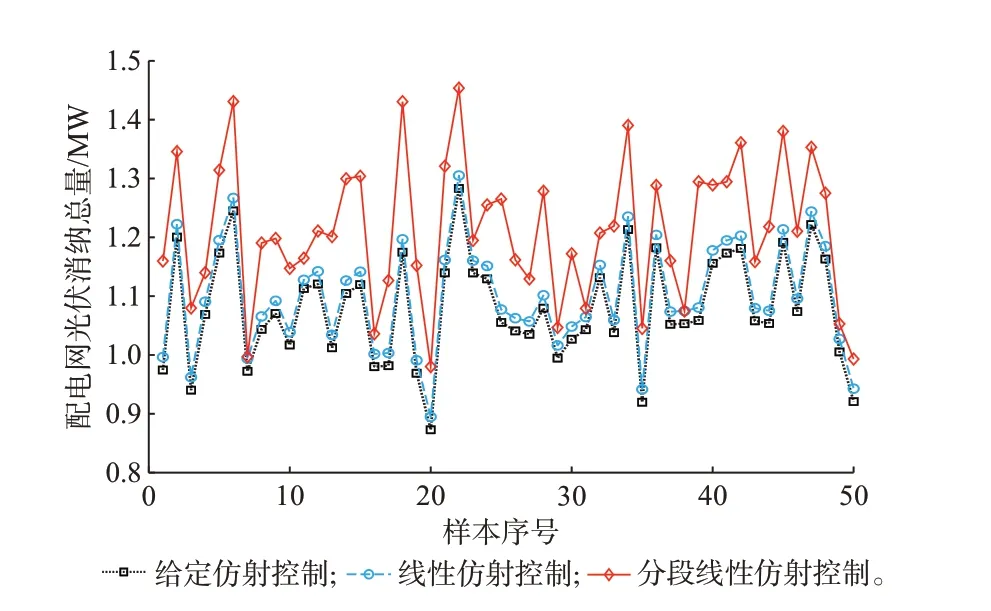
图5 光伏消纳量对比Fig.5 Comparison of photovoltaic accommodation
4.6 三相电压安全约束验证
为验证本文所提方法对电压安全约束的有效性,对未使用和使用升维分段线性仿射控制的IEEE 123 节点配电网三相电压分别进行蒙特卡洛模拟。其中,前者光伏出力波动范围为0~0.4 MW,后者光伏出力波动范围受到功率安全波动区间约束。由于在三相系统中,并非所有节点的三相均可用,为了保证曲线的连贯性,直接省略该相中不存在的节点。
附录D 图D4 至图D6 表示100 次蒙特卡洛模拟中各相电压分布情况,颜色越深则概率越高。其中,未使用本文方法时,a 相、c 相均出现电压越限情况;使用本文方法后,电压越限得到有效抑制。因此,所提方法能够保证在光伏功率安全波动区间内,全网电压在安全约束范围之内。
4.7 求解时间
以下数据均为采用MATLAB+Yalmip+Gurobi求解得到,所用计算机的CPU 为AMD Ryzen 7 4800H,集成了Radeon 显示处理器(2.90 GHz)。
表2 列出了各方法求解IEEE 123 节点配电网优化问题的时间,其中,光伏数量为20 的算例的具体接入信息见附录F 表F1。对于给定仿射控制,优化模型为简单的线性规划问题,求解速度很快;相较于原本优化模型的规模,光伏数量增加所引入的额外约束数量可忽略,因而光伏数量增加对于求解时间基本无影响。对于线性仿射控制以及升维分段线性仿射控制,优化模型是混合整数规划问题,光伏数量增加会使得混合整数的约束数量增加,导致求解时间增加。在装有上百台光伏的真实配电网中,光伏多为部分可控,而对于数十台可控光伏的情况,本文所提模型的求解时间是可接受的,对于15 min~1 h的控制时间间隔仍具有工程实用性。此外,对具有大量光伏的配电网,可采用算力更强的硬件设备加速计算过程,进一步保证工程实用性。
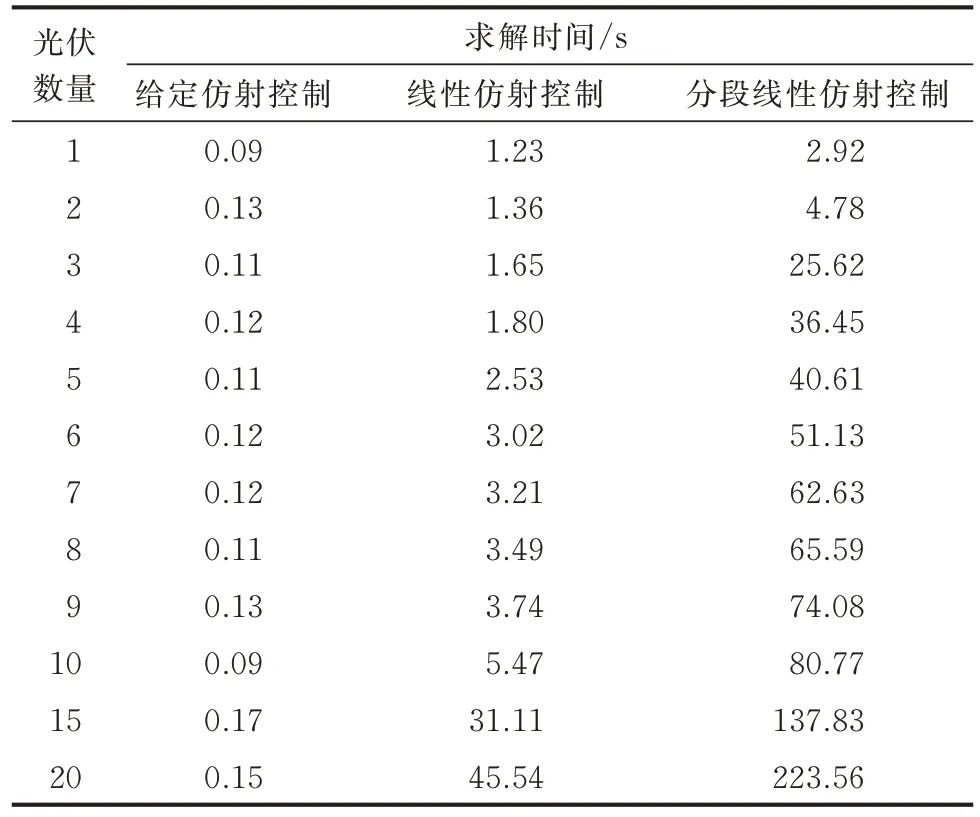
表2 优化模型求解时间Table 2 Solving time of optimization models
5 结语
本文提出了考虑配电网电压约束的光伏功率升维仿射控制方法,构建并优化了光伏就地控制的功率安全区间,以明确电压约束对光伏功率的波动限制,提升配电网光伏消纳能力。采用IEEE 123 节点三相配电网进行仿真分析,所提升维分段线性仿射控制策略在光伏功率安全波动区间内能够保证电压不越限。通过与给定仿射控制、线性仿射控制的结果进行对比,证明其能够扩大配电网光伏功率安全波动区间,区间范围增加38.41%;可提升光伏消纳量达22.28%;升维分段线性仿射控制的优化模型求解时间在可接受范围内,证明其具有工程实用性。
本文所提光伏控制策略能从整体上提高配电网功率安全波动区间范围,但并未考虑处于首末端节点光伏功率安全波动区间设置的公平性。后续研究将考虑不同位置光伏功率波动对节点电压的差异化影响,研究更为公平的安全波动区间构建方法。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

