基于电压时空聚合曲线的乡镇配电台区户变关系识别方法

唐冬来，李 强，陈永东，张 捷，刘友波，宋卫平

（1.四川中电启明星信息技术有限公司,四川省成都市 610074；2.国网信息通信产业集团有限公司,北京市 102211；3.四川大学电气工程学院,四川省成都市 610065）

0 引言

户变关系是指用户电表（residential electricity meter,REM） 与 配 电 变 压 器（distribution transformer,DT）之间的连接关系,是计算配电台区（distribution station area,DA）线损、故障定位等研究的基础［1-2］。低压线路是REM 的接入节点,具有网络结构复杂、变动频繁等特点［3-4］。供电公司在办理REM 新装、迁址、更名等业扩报装时,现场人员因低压线路变动频繁,易将REM 挂接在错误的低压线路下,从而造成户变关系不一致［5-6］。因此,须开展有效的户变关系识别研究。

2018 年以来,国家电网有限公司开展了以高速电力线载波（high-speed power line carrier,HPLC）技术为基础的智能电表建设工作,通过HPLC 技术实现了REM 日96 点频次的电气量数据采集,为户变关系识别提供了数据基础［7-8］。目前,基于智能电表HPLC 技术的户变关系识别包括特征脉冲信号识别和电气量相似性识别两类［9-10］。特征脉冲信号识别方法基于HPLC 不能跨DT 通信的原理,通过配电台区融合终端（fusion terminal of distribution station area,FTDA）向REM 发送HPLC 特征脉冲信号的方式进行识别［11］,但存在信号传输衰减大、共用零线DA 信号串扰等问题,造成户变关系识别准确率低［12］。电气量相似性识别方法基于REM 和DT 低压出线电气量变化相似的原理,采用皮尔逊相关系数、离散Frechet 距离、离群点等算法比较REM 和DT 低压出线电压曲线变化的相似度,从而判断户变关系［13-15］。但随着屋顶光伏、储能等分布式能源大规模接入DA,造成DA 潮流多向,REM 的电压变化规律将与DA 内多个电源点的发电出力、电源点到REM 的低压线路距离相关［16］。其中,电源点发电出力越大,对REM 电压波动曲线影响越大,反之则影响越小；电源点到REM 的低压线路越长,其线路阻抗越大,电压波动衰减越大,对REM 电压波动曲线影响越小,反之则影响越大。因此,分布式能源接入DA 后,REM 和DT 电压曲线相关性变弱,电气量相似性识别方法不能有效识别户变关系。

为解决含分布式能源DA 中存在的DT 低压出线与REM 电压曲线相关性变弱、户变关系识别准确率低的问题,提出了一种基于电压时空聚合曲线的户变关系识别方法。通过行波特征信号测距,实现REM 到FTDA、分布式能源的低压线路距离测量,并将其作为电压波动曲线压降损耗的计算基础。在此基础上,综合考虑DA 内多个分布式能源电压波动及REM 到FTDA、分布式能源的低压线路距离,采用时空聚合方式获得REM 位置的理论电压波动曲线,并与REM 实际电压波动曲线比较相似度,从而识别户变关系。

1 户变关系识别流程

本文所提基于电压时空聚合曲线的户变关系识别方法分为DA 设备拓扑测距、户变关系识别两部分,其流程图如图1 所示。

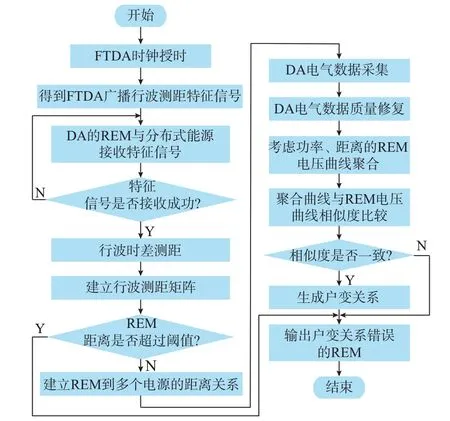
图1 户变关系识别流程图Fig.1 Flow chart of user-transformer relationship identification

1）DA 设备拓扑测距

DA 设备拓扑测距的目的是测量REM、光伏、储能等设备到DT 之间的低压线路长度,为DA 电压时空曲线聚合提供电压压降损耗的数据基础。该方法通过计算DT 到DA 设备的行波测距特征时间差来测量其长度。

2）户变关系识别

首先,对采集的DA 设备电气数据质量进行修复；然后,考虑DA 电源功率、电源到户表线路长度,采用时空聚合方式获得用户电表位置的理论电压波动曲线；最后,将该曲线与REM 的实际电压波动曲线进行相似度比较,从而识别户变关系。

2 户变关系识别建模

2.1 DA 设备拓扑测距

2.1.1 FTDA 时钟授时

行波测距方法需测距的两端设备都具备高精度的时钟对时功能。全球定位系统（global positioning system,GPS）向REM 时钟授时的精度为1 μs,而在电力线中信号的传播速度为300 m/μs,即行波测距误差为300 m［17-18］。按照中国DA 供电半径为500 m计算,该误差将严重影响户变关系识别精度。北斗卫星在亚太地区的单向时钟授时精度为100 ns,即行波测距误差为30 m［19-20］。2020 年,国家电网有限公司启动了符合国际标准的新一代智能电表建设工作,在FTDA、分布式能源和REM 中均配置了北斗对时模块［21］,为本文研究提供了规模化应用基础。因此,本文采用北斗卫星授时,以提高授时精度,降低测距误差。

FTDA 是安装在DT 侧的物联管理设备,可实现对DT、REM、分布式能源、漏电保护器等设备的数据采集、边缘分析等功能［22］。本文采用FTDA 向分布式能源、REM 进行授时。

FTDA 接收主站时间同步装置的对时命令后,向REM 等 设 备 广 播 带 时 间 戳ta的 对 时 信 号［23］。REM 等设备记录FTDA 对时信号到达的时间戳tb,并增加向FTDA 反馈发送时间戳tc的时对信号,FTDA 接收REM 对时反馈信号的时间戳td,则REM 的时钟对时误差th为:

式中:na为DA 分布式能源的个数,FTDA 按分布式能源的数量发送相同数量的对时指令；tbp为对时组p的REM 记录对时信息到达的时间；tcp为对时组p的REM 向FTDA 反馈对时信号的时间戳；tdp为FTDA接收对时组p的REM 反馈指令的时间戳。

在获得REM 对时误差后,将每个电表的时钟增加时钟对时误差,则REM 时钟时间Te可表示为:

式中:tf为FTDA 对时的时间。

2.1.2 REM 线路长度测距

电力线行波测距是一种测量电力线设备之间长度的方法,该方法通过行波脉冲信号在电力线的传输时间来估算距离［24-25］。行波测距是指在DT 的FTDA 和电表HPLC 模块增加行波测距功能,当FTDA 发射行波测距特征信号时,信号以光速沿低压线路传播,当REM 接收到行波测距特征信号后,根据发射、接收的时间差可计算出FTDA 与REM之间的距离。本文方法在FTDA 和分布式光伏、储能等电源点均安装行波测距模块,通过计算电源点到REM 之间的低压线路长度,为DA 电压时空曲线聚合的电压压降损耗影响因子提供基础数据。

DA 分为乡镇DA 和城市DA 两类。乡镇DA 为辐射型台区,供电半径较大,REM 之间较为分散。因此,采用行波测距特征信号计算FTDA 与REM之间距离的相对误差小。城市DA 供电半径小,一个DA 对应一栋或多栋楼房,且REM 表箱多为集中安装,采用行波测距特征信号计算FTDA 与REM之间的相对误差大。同时,部分DA 低压线路共用零线,造成行波测距特征信号跨DA 串扰。因此,行波测距特征信号不能直接用于户变关系识别。另外,DA 供电半径通常在500 m 内,行波测距30 m 的误差会造成DA 部分户变关系识别错误,针对此类REM,本文DA 设备拓扑测距仅用于电压时空曲线聚合中的压降损耗计算,不作为户变关系识别的直接依据。需增加电压时空聚合曲线相似度比较来进行户变关系识别。

本文结合行波测距特征信号不能跨变压器传输和零线耦合的特点,引入低压线路长度阈值和电压时空聚合曲线结合的方式进行户变关系识别。FTDA 分别在低压线路三相上发射行波测距特征信号,该信号先沿同相传播到低压线路末端,并通过零线耦合到其他两相。单相REM 接收同相的行波测距特征信号时间最短,接收其他两相的行波测距特征信号时间较长。因此,可通过REM 接收最短行波测距特征信号时间来进行单相REM 线路长度测距和相位识别。三相REM 接收三相的行波测距特征信号时间相等,可通过三相REM 接收行波测距特征信号的平均时间计算三相REM 与FTDA 或分布式能源的低压线路长度。

单相REM 到FTDA 的距离da为:

式中:tk,min为单相REM 接收FTDA 的最短行波测距特征信号时间；tl为FTDA 的行波测距特征信号发射时间；va为行波测距特征信号在不同介质线路中的传播速度。

三相REM 到FTDA 的距离db为:

式中:nb为0.4 kV 的三相REM 数量；toj为不同相位下三相REM 接收到FTDA 行波测距特征信号的时间；tpj为不同相位下FTDA 的行波测距特征信号发射时间；vb为行波测距特征信号在不同介质线路中的传播速度。

分布式能源测距与REM 相同,本文不再赘述。

2.1.3 建立REM 到多个电源的距离矩阵

建立REM 到多个电源的距离矩阵是为了分析线路长度对REM 电压曲线波动影响的重要程度。在分布式能源输出电流相同的情况下,线路长度越短,阻抗越小,REM 电压曲线波动影响越大,反之则影响越小。

REM 到FTDA、分布式能源的距离矩阵Ld为:

式中:dal为REM 到FTDA 的线路长度；dm为REM到DA 第m个分布式能源的线路长度。

在DA 中,REM 到FTDA、分布式能源的低压线路距离小于供电半径。因此,可将DA 供电半径作为户变关系识别的初步筛查条件。若REM 到FTDA、分布式能源的低压线路距离大于DA 供电半径,则该REM 不属于此DA。因此,当REM 到FTDA 的线路长度小于阈值Δf1时,说明该REM 属于此DA。若REM 到FTDA、分布式能源的低压线路距离小于DA 供电半径,则存在REM 属于此DA或临近DA 的REM 接收到串扰信号。该情况下,需结合REM 的电压时空聚合曲线做进一步识别。

2.2 户变关系识别

2.2.1 DA 电气数据修复

REM 按15 min/次的频率采集电气量测数据,在数据采集和传输的过程中,易受到噪声影响,造成错误、缺失等异常情况。因此,在户变关系识别前,需对采集数据进行修复。

沙维斯基-格雷（Savitzky-Golay,SG）滤波器是一种噪声数据处理方法,该方法采用卷积实现噪声数据的处理,通过线性最小二乘法将噪声相邻数据点的连续数据进行多项式拟合,从而实现平衡数据去噪的目的［26-27］。该滤波器能在不改变REM 电气量测数据变化趋势的情况下提高数据精度。因此,采用SG 滤波器对DA 量测数据进行数据修复。

REM 测量窗口数据为fj,数据幅值的取值范围为[-z,z]。通过构造ka阶多项式来拟合上述数据,拟合后的REM 测量窗口数据ha为:

式中:cs为第s阶的REM 测量窗口数据；tka为REM测量时间的ka次方。

拟合后的REM 数据与原值的残差平方和hd为:

式中:har为拟合后的幅值r的REM 测量窗口数据；fjr为幅值r的REM 测量窗口原始数据。

采用最小二乘法计算REM 测量窗口数据的目的是求解最优的拟合效果,使残差平方和最小,即残差对多项式系数的偏导为0。当REM 测量数据拟合的单边数、阶数及待拟合的数据明确后,通过估计窗口内中心点值并不断移动窗口完成数据修复。该过程相当于对输入SG 滤波器的REM 单位冲击响应数据进行卷积,得到滤波后的数据he为:

式中:ec为最小二乘法多项拟合次数；fjk为输入SG滤波器的幅值k的原始数据；gk为幅值k的REM 测量数据拟合平滑系数。

2.2.2 DA 电压曲线聚合

分布式能源高比例接入DA 后,DA 的潮流由单向流动变为多向流动。REM 电压曲线的变化与DA 多个电源出力、电流流向、低压线路长度等因素相关。因此,DA 电压曲线聚合的目的是考虑DA 电源的多种影响因素,计算REM 当前位置的理论电压波动曲线,并将其作为户变拓扑识别关系的基础。在此基础上,将REM 当前位置的理论电压波动曲线与REM 实际的电压波动曲线进行相似度比较,从而识别户变关系。

本文方法计算REM 理论电压波动曲线时,采用式（5）中REM 到FTDA、分布式能源的低压线路长度计算电压时空曲线聚合中的电压压降损耗,而非直接采用完整的DA 户变关系。因此,在计算REM 理论电压波动曲线时,无须输入DA 户变关系。REM 理论电压波动曲线的计算变量包括REM到FTDA、分布式能源的低压线路长度,低压线路单位电阻值,DA 低压线路出线首端,分布式能源,REM 的电压、有功功率、无功功率。

针对含分布式能源的辐射型DA 进行电压曲线聚合分析,其典型结构如图2 所示。图中:DA 有m个分布式能源、n个REM；FTDA 测量的DA 低压线路出线首端电压为u0；第m个分布式能源的电压为uam,电源功率出力为pam；第n个REM 的电压为un,用电功率为pn。在分布式能源中,分布式光伏只有发电出力,其电压波动曲线会使REM 电压有不同程度的上升。分布式储能在充电时等同于用户负载,会使REM 电压降低,分布式储能电压波动曲线与DA 的0.4 kV 出线首端电压相似；在分布式储能放电时,会使REM 电压上升,其对REM 电压影响等同于分布式光伏。第n个REM 到DT、分布式能源的线路长度由式（5）得出。

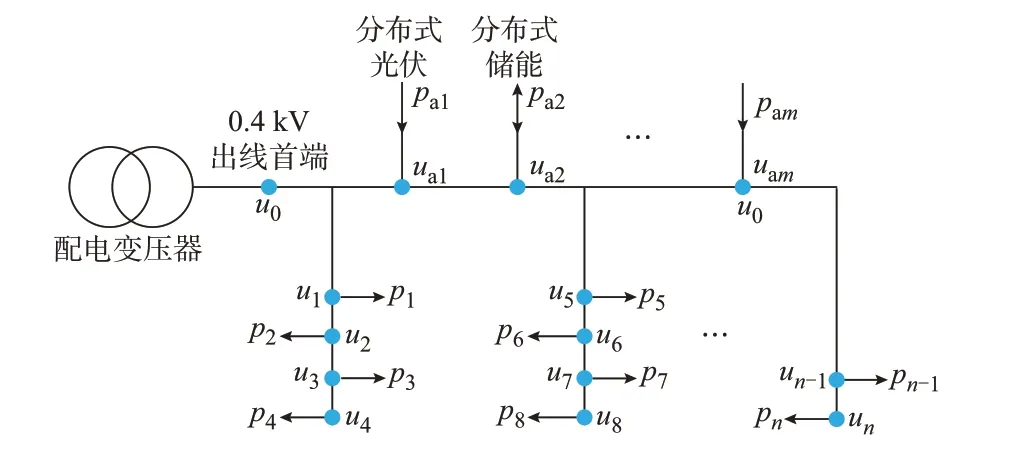
图2 辐射型DA 结构Fig.2 Structure of radiant-type DA

在DA 分布式能源并网前,REM 的电压压降与低压线路长度成正比,即REM 电压波动曲线与DA的0.4 kV 出线首端电压u0相似,低压线路越长,则低压线路阻抗越大,电压波动曲线衰减越大,REM的电压压降也越大；反之,低压线路越短,则低压线路阻抗越小,电压波动曲线衰减越小,REM 的电压压降也越小。在分布式能源并网后,假定分布式能源的光伏与储能并网只有有功功率,REM 的电压将升高,其电压与DA 多个分布式能源的功率、REM离多个电源点的低压线路长度等相关。因此,REM的电压波动曲线与DA 内的多个电源功率、离电源点的低压线路长度、低压线路单位电阻值有关。

DA 供电半径为500 m,不同线径、材质的导线电阻值差异较小。假定不同材质的导线电阻值相同,低压线路每米电阻值为ra,电源点到第n个REM的低压线路长度为oan,则分布式能源并网前,从电源点到第n个REM 线路的线损Lln为:

式中:qn为第n个REM 的无功功率。

在分布式能源并网后,从m个电源点到第n个REM 线路的线损Ls为:

式中:pan为电网提供给第n个REM 的有功功率；pfw为DA 的分布式能源w提供给第n个REM 的有功功率；qan为电网提供给第n个REM 的无功功率；uan为第n个REM 的电压；oanw为DA 的分布式能源w到第n个REM 的低压线路长度。DA 分布式能源并网容量越大,DA 负荷消纳分布式能源越多,线损越小。当分布式能源并网容量大于DA 负荷时,将出现DT 功率倒送的情况。

在DA 分布式能源并网前,REM 电压压降Δuz为正,且和低压线路长度成正比。第n个REM 的初始理论电压uzn为:

式 中:un-1为 第n-1 个REM 电 压,若 为DA 第1 个REM,则为DA 低压线路出线首端电压u0。按REM距DA 低压线路出线首端的距离依次进行计算,可获得DA 内所有REM 的初始理论电压。

分布式能源并网后,假定分布式能源只提供有功功率,第n个REM 的初始理论电压ugn为:

由式（12）可见,当DA 分布式能源并网后,REM 的电压将提升,提升的电压与DA 内的多个电源功率、离电源点的线路长度相关。

假定分布式能源并网前后,REM 的功率不变,第m个分布式能源对第n个REM 电压波动曲线影响包括从第m个电源点到第n个REM 线路的线损和REM 影响两部分,其对REM 电压曲线波动影响的权重wm为:

式中:pbw为DA 的分布式能源w提供给第n个REM的有功功率。

电压时空聚合是一种考虑多种因素的REM 电压曲线拟合方法,该方法将REM 的电压时空维度数据聚合成平滑的电压波动曲线。其中,在时间维度上,REM 的电压波动曲线与DA 内DT 低压出线、多个分布式能源发电、储能放电的电压波动曲线相关；在分布式能源并网前的时间段,REM 电压波动曲线仅与DT 低压出线电压波动曲线相关；在分布式能源并网后的时间段,REM 电压波动曲线与DA内DT 低压出线、多个分布式能源发电、储能放电的电压波动曲线和权重相关。因此,时间维度聚合即将DA 内多个电源对REM 影响的电压波动曲线进行聚合。在空间维度上,REM 的电压波动曲线与低压线路长度的压降相关；在分布式能源并网前,REM 电压波动曲线仅与REM 到DT 低压出线的长度电压压降损耗相关；在分布式能源并网后,REM电压波动曲线与DA 内DT 低压出线、多个分布式能源发电、储能放电到REM 低压线路长度的电压压降损耗相关。因此,在空间维度上将DA 内多个电源到REM 的线路长度进行聚合。电压时空聚合方法可计算DA 多电源、低压线路长度对REM 电压波动影响的理论值,以便观测电压时空数据的内在关联,掌握DA 数据变化关系。

最小二乘渐进迭代逼近（least square progressive and iterative approximation,LSPIA）方法是一种曲线拟合方法,该方法采用调整迭代控制点构建逼近真实值的曲线,并将其收敛到最小二乘法的拟合结果［28-29］。LSPIA 方法计算效率高,用于处理大规模的配电台区REM 数据集,但本文DA 内多个电源的电压波动、距离REM 的低压线路长度对REM 电压波动影响不同。因此,本文在LSPIA 的基础上,增加不同DA 电源拟合数据的权重,从而计算出REM 的理论电压波动曲线。

式中:Al(t)为控制次数l的REM 理论电压曲线基函数。

在加权LSPIA 首次迭代中,计算第i点电压数据点对应的差γ:

式中:Ui（t）为初始REM 理论电压曲线第i点电压值。

加权LSPIA 迭代的调整量Δuf为:

式中:no为DA 电源点的数量；wo为式（13）中DA 电源点o对REM 影响的权重；Ao(t)为DA 电源点o的REM 理 论 电 压 曲 线 基 函 数；γo为DA 电 源 点o电 压曲线与REM 理论电压曲线的向量差；λ为加权LSPIA 的常数。

在此基础上,定义REM 理论电压曲线的控制顶点集合sb:

在首次迭代后,REM 理论电压曲线控制点由初始控制点和调整量Δuf计算而得,第2 次的迭代控制点通过式（18）计算而得,加权LSPIA 不断迭代,直至拟合的REM 理论电压波动曲线满足精度Δf2。

2.2.3 REM 电压曲线相似度比较

在DA 内,REM 的电压变化关系与多个电源点的变化关系相关。因此,可将REM 理论电压波动曲线与实际的电压波动曲线进行比较,若两者的变化关系相似,则该REM 属于此DA；反之,则不属于该DA。

多线位置距离（locality in-between polylines,LIP）是一种曲线相似性度量方法,该方法通过计算两条REM 电压波动曲线之间的面积来判断其相似度:若面积为0,则表明两条REM 电压波动区域完全一致；面积越大,则表明两条REM 电压波动曲线相似度差异越大,LIP 方法抗干扰能力强［30］。因此,采用LIP 计算REM 理论电压波动曲线与实际的电压波动曲线之间的相似度。

REM 理论电压波动曲线与实际的电压波动曲线之间的相似度Ba为:

式中:np为REM 理论电压波动曲线与实际的电压波动曲线之间构成的多边形个数；Eab为REM 两条电压曲线构成的多边形b的面积；wab为多边形b的权重。

权重由REM 两条电压曲线构成区域周长占比总曲线总长度决定,则权重wa可表示为:

式中:dx和dy分别为REM 理论和实际电压波动曲线的长度；dxa和dya分别为REM 理论和实际电压波动曲线交叉区域部分的电压波动曲线的长度。

当REM 理论电压波动曲线与实际的电压波动曲线之间的相似度大于Δf3时,则说明该REM 属于此DA。

3 算例分析

以中国某地区乡镇示范DA 验证本文方法。该DA 配置一台DT,容量为800 kV∙A；8 户光伏发电用户,额定发电功率为42 kW；1 户储能用户,额定功率为10 kW,容量为20 kW∙h；327 个REM,其中,单相REM 为314 个,三相REM 为13 个,DA 供电半径为800 m。为模拟HPLC 信号DA 串扰的情况,将该DT 与临近的DT 出线零线连接在一起,连接零线长度为710 m。为模拟电压时空聚合曲线识别,在档案中分别设置DA 的276 个单相REM 和26 个三相REM,其数据来源于共用零线的配电台区REM。用于户变关系识别的数据来源于2023 年3 月。

本文算例仿真服务器采用Intel Xeon Gold 6143处理器,频率为2.8 GHz,核心数量为16 个,内存为32 GB,硬盘容量为20 TB。软件操作系统为Windows Server 2019,采用Python 开发本文算法。DA 线路长度阈值Δf1设置为800 m；拟合的REM 理论电压波动曲线精度Δf2、DA 电流差异阈值Δf4、电量差异阈值Δf5均按0.2 级电表精度设置为0.2%。REM 理论与实际的电压波动曲线之间的相似度阈值Δf3设置为DA 末端线路实测值95%。行波测距信号在低压线路中的传播速度设定为300 m/μs,所提方法与自适应分段聚合近似（adaptive piecewise aggregate approximation,APAA）［31］、关 联 卷 积［32］、密度拓扑聚类［33］等主流户变关系识别方法进行比较。

3.1 模型基础数据分析

3.1.1 DA 设备时钟授时精度分析

DA 的分布式能源、REM 时钟授时精度是本文方法的基础,其计算方法为:采用具有双模卫星接收功能的FTDA 接收北斗卫星、GPS 时钟信号,并向REM、分布式能源分别进行授时。采用电能表现场校验FTDA、REM、分布式能源的时钟与北斗或GPS 时间误差。

采用FTDA 接收北斗和GPS 卫星信号,并向DA 的327 个REM、8 个分布式屋顶光伏、1 个储能进行时钟授时,并比较两者的时钟授时精度,DA 设备时钟授时精度分析如附录A 图A1 所示。

由附录A 图A1 可见,FTDA 接收北斗信号时采用了星基增强技术进行校验,从而获得标准时间,在DA 广播对时中增加了分布式能源的对时校准,DA 时钟授时精度平均约90 ns,且散布较小。而GPS 授时中,FTDA 接收GPS 信号和广播对时指令时均无对时校准,DA 时钟授时精度平均约800 ns,且散布较大。因此,北斗卫星的授时精度更高。

3.1.2 REM 线路长度测距精度分析

REM 线路长度测距分析是估算REM 归属DA的核心数据之一。若REM 线路长度超过DA 供电半径,则存在户变关系错误的问题。本文方法中,FTDA 通过发射行波测距信号进行REM 线路长度测距；密度拓扑聚类算法的GPS 测距中,通过计算配电台区REM 到DT 的地理坐标差来估算REM 线路长度距离。将上述距离和DA 施工图中的REM线路长度距离进行比较。

采用FTDA 发送行波测距信号和GPS 测距方法,分别向DA 的327 个REM、8 个分布式屋顶光伏、1 个储能进行测距,并比较两者的测距精度,REM 线路长度测距精度误差如附录A 图A2 所示。

由附录A 图A2 可见,本文方法在REM 线路长度测距时,通过两个终端的时间差乘以行波测距信号的传播速度计算,其计算精度与DA 设备时钟授时精度相关,所提方法的REM 线路长度测距精度平均为18 m,而GPS 测距时,通过GPS 卫星定位了REM 和DT 之间的地理坐标位置,但低压线路并非沿直线架设,架设长度大于地理坐标位置之差,同时GPS 定位也存在50 m 的位置误差,其REM 线路长度测距精度平均为60 m。因此,本文方法的REM线路测距精度高于GPS 方法。

3.1.3 REM 到多个电源的距离矩阵

REM 到多个电源的距离矩阵是计算REM 时空聚合曲线的基础,通过REM 线路长度测距形成了REM 到DA 多个电源的距离矩阵。本文以第1 个REM（x1）为例进行说明,REM 到多个电源的距离矩阵如附录A 表A1 所示。

由附录A 表A1 可见,本文方法建立了REM 到DT、屋顶光伏、储能的低压线路长度距离表。由附录A 图A2 可知,所提方法线路测距精度优于GPS方法,所以,所提方法REM 到多个电源的距离表较GPS 更准确。

3.1.4 DA 电气数据修复分析

DA 电气数据修复是为了减少REM 缺失和噪声数据对户变关系识别的影响。SG 滤波器的窗口数据和多项式阶数的参数选择上,若取值越大,修复REM 数据越接近真实数据；但在窗口数据固定的情况下,多项式阶数较大时,会出现将REM 曲线拟合成直线的情况。因此,在满足窗口数据长度的情况下,以拟合残差最小为目标,进行参数选择,设定窗口数据为7,多项式阶数为3。

以单相REM（x1）的2 天电压数据为例,人为模拟第1 天01:15—02:00、08:15—09:00 和 第2 天12:15—13:00、22:15—23:00 的缺失数据,采用SG滤波器进行REM 电压数据修复,REM 电压数据修复结果如附录A 图A3 所示。

由附录A 图A3 可见,原始REM 电压曲线中存在4 h 的缺失数据。通过SG 滤波器进行数据修复后,有效地补正了缺失数据,并保留了REM 电压曲线的基础形态。

3.2 户变关系识别分析

3.2.1 REM 电压波动曲线影响权重分析

REM 电压波动曲线影响权重分析的目的是评估DA 内各电源对电压波动曲线影响占比。计算方法为:以24 h 为例,在计算DA 电源对REM 电压曲线波动影响权重计算中,DT 上级线路提供的电源时间段为24 h,8 户屋顶光伏发电的时间段为07:00—18:00,储能充电的时间段为00:00—06:00,储能放电的时间段为19:00—21:00。DA 设备功率如图3 所示。

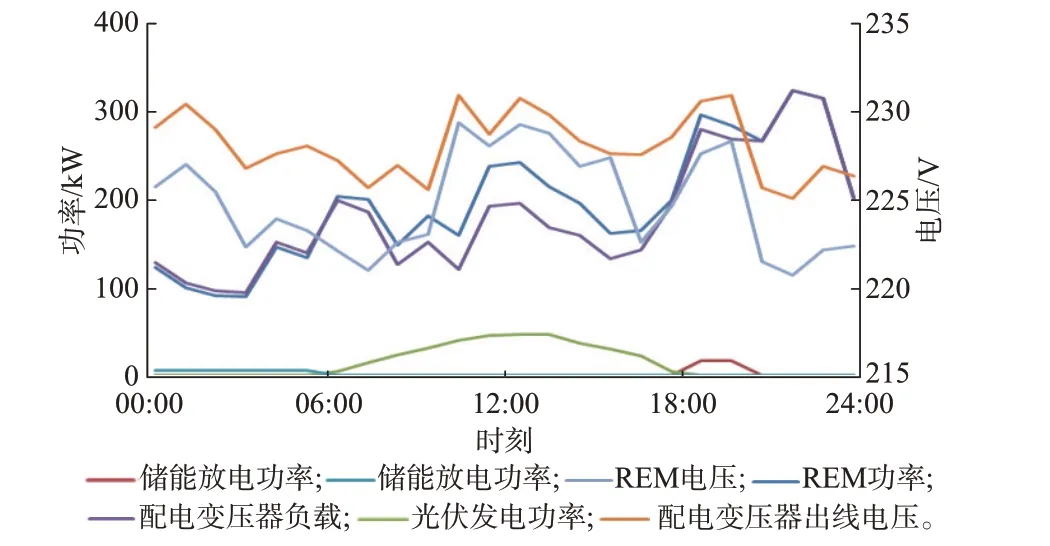
图3 DA 设备功率Fig.3 Power of DA equipment

由图3 可见,DA 在00:00—06:00 时段屋顶光伏未发电、储能未放电,该时间段内DA 对储能进行充电,储能在充电时等同于用户负载,会使REM 电压降低,储能、REM 电压与DT 低压出线电压相关；在07:00—18:00 时段,屋顶光伏发电,此时间段内REM 电压与DT、屋顶光伏不同时段发电功率相关；在19:00—20:00 时段,储能放电,REM 电压与DT 负载、储能的放电功率相关；在21:00—24:00时段,REM 电压与DT 低压出线电压相关。

根据DT 负载功率、屋顶光伏发电出力、储能放电功率计算不同时间段的影响权重。DA 电源影响REM 电压权重如附录A 表A2 所示。

由附录A 表A2 可见,DA 内8 个屋顶光伏在07:00—18:00 时段发电,不同的屋顶光伏发电功率均有差异。因此,对REM 电压波动曲线影响权重不同。储能在19:00—20:00 时段放电,根据储能放电功率计算出对REM 电压波动曲线影响权重。

3.2.2 DA 电压曲线聚合分析

DA 电压曲线聚合分析的目的是验证加权LSPIA 计算REM 理论电压波动曲线过程。其计算方法为:将DA 出线、光伏发电、储能放电的电压波动曲线输入模型,计算REM 的理论电压波动曲线,并将该曲线与REM 实际电压测量值进行比较,两者形状越接近,则REM 电压曲线聚合越准确。

以单相REM 的24 h 电压波动情况为例,输入附录A 表A1 中的REM 到多个电源的距离、附录A表A2 中DA 电源影响REM 电压权重、图3 中DA 设备功率数据,采用本文方法计算REM 理论电压波动曲线,初始迭代拟合REM 电压波动曲线如附录A图A4 所示。迭代误差如附录A 图A5 所示。

由附录A 图A4 可见,日电压曲线中,日96 点曲线的第1 和第96 点不进行控制,即控制顶点数为94。如附录A 图A5 可见,须迭代22 次才能满足误差率0.2%的要求。经过迭代后的REM 电压曲线聚合结果如图4 所示。

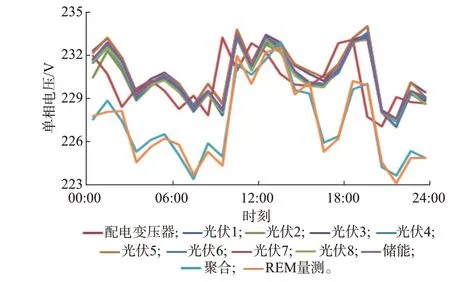
图4 REM 电压曲线聚合结果Fig.4 Voltage curve aggregation results of REM

由图4 可见,通过电压时空聚合,REM 理论电压波动曲线接近REM 的真实电压波动曲线,且误差率小于0.2%。由此可见,通过电压时空聚合曲线可获得准确的REM 电压波动值。

3.2.3 REM 电压曲线相似度比较分析

REM 电压曲线相识度比较是户变关系识别的核心,本文LIP 方法采用两条曲线相交面积比较REM 理论与真实电压波动曲线相似度；APAA、关联卷积、密度拓扑聚类方法采用两条曲线形态相似度比较REM 理论与真实电压波动曲线相似度；REM 电压曲线相似度比较如附录A 图A6 和表A3所示。

由附录A 图A6 和表A3 可见,LIP 方法计算出REM 理论与真实电压波动曲线相交的y1和y12共12 个曲线面积来判断其相似程度,两条曲线的相似度为99.8%；APAA、关联卷积、密度拓扑聚类方法比较REM 理论与真实电压波动曲线相似度时,在分布式能源并网前的00:00—06:00、21:00—24:00时段,电压波动曲线相似度分别为99.3%、99.1%、99.2%,REM 理论与真实电压波动曲线相似度较高；在分布式能源并网后的07:00—20:00 时段,电压波动曲线相似度分别为94.4%、94.1%、94.1%,REM 理论与真实电压波动曲线相似度较低。因此,在分布式能源并网后,LIP 方法较APAA、关联卷积、密度拓扑聚类方法的REM 理论与真实电压波动曲线相似度更高。

3.2.4 户变关系识别准确率分析

户变关系识别准确率是本文方法的核心指标,其计算方法为:将示范DA 的零线与临近的DT 出线零线相连,在示范DA 的327 个REM 的数据中分别增加DA 的276 个单相REM 和26 个三相REM,DA 的REM 总数为629 个,然后采用算法识别户变关系,算法识别结果与真实的户变关系一致则为准确,算法识别准确的户变关系和识别总数的比值即为户变关系识别准确率。

分别采用本文方法与APAA、关联卷积、密度拓扑聚类方法比较户变关系识别准确率,结果如表1 所示。

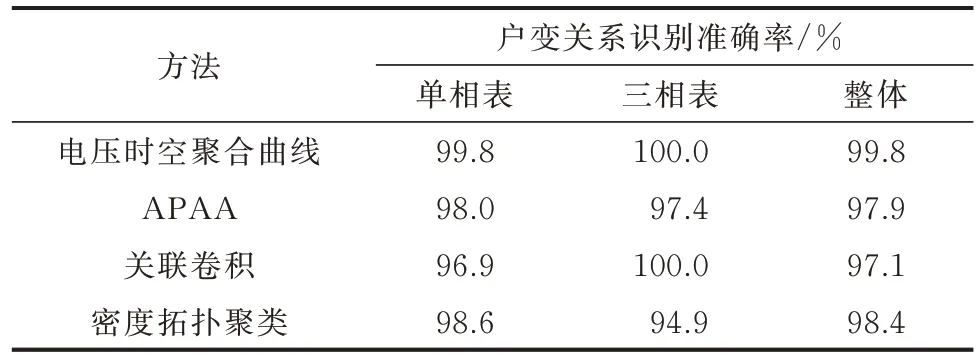
表1 户变关系识别准确率Table 1 Accuracy rate of user-transformer relationship identification

由表1 可见,本文方法采用REM 电压曲线计算户变关系时,考虑了DA 分布式能源对电压的影响,户变关系识别准确率为99.8%,而APAA、关联卷积、密度拓扑聚类方法直接采用DT 低压出线的电压波动曲线与REM 电压波动曲线进行比较,在此过程中分布式能源对REM 电压波动曲线造成影响,导致户变关系识别分别为97.9%、97.1% 和98.4%。由此可见,本文方法识别更准确。

4 结语

为解决含分布式能源DA 中存在的DT 低压出线与REM 电压曲线相关性弱、户变关系识别准确率低的问题,提出了一种基于电压时空聚合曲线的户变关系识别方法。该方法具有以下特点:

1）采用行波测距方法计算了REM 到DT、分布式能源的线路长度,并将其与DA 供电半径进行比较,识别异常线路长度的REM。

2）分析了分布式能源并网、REM 线路长度对REM 电压造成的影响,通过电压时空曲线聚合获得REM 理论电压波动曲线,该曲线具有误差小的特点。

3）采用REM 理论与REM 真实电压波动曲线进行比较的方式识别户变关系准确率,其准确率达99.8%。

所提方法能有效地提高含分布式能源DA 户变关系识别成功率。但本文研究需24 h 的REM 电压波动曲线,不适用频繁切换REM 相位关系的换相开关型DA。下一步,将提高REM 采集频次,在换相开关型DA 切换周期内实现DA 户变关系识别。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。