基于脉冲观测器的多智能体系统的领导跟随一致性

胡 然，彭世国

（广东工业大学 自动化学院, 广东 广州 510006）

多智能体系统的协同控制因其在无人机作战、机器人编队等方面的广泛应用而得到关注。作为其中一个重要的研究分支，领导跟随一致性问题在近几年取得了大量的研究成果[1-6]。

多智能体系统中大多数一致性控制算法是根据各智能体状态信息设计的，当这些信息不可用时，此类控制器的设计将会受到限制。为解决上述问题，基于状态观测器的控制方法被提出，如文献[7]根据滑模观测器估计的状态信息构建了分布式控制协议。类似地，如果在领导跟随多智能体系统中领导者状态信息不可用时，需要设计相应的观测器来观测[8]。值得注意的是，上述观测器的设计依赖于输出向量的连续测量，这样会造成信道的拥堵和较高的控制成本。

输出向量是否能够只在某些离散时刻获取，同时设计出相应的观测器？答案是肯定的。脉冲观测器于2007年首次被Raff[9]提出，它只需要观测器状态在离散时刻进行更新。相比连续测量的观测器，这大大减少了观测器与系统之间的信息交互，节省了通信带宽。近年来，脉冲观测器逐步得到重视。例如，为实现时滞系统的稳定，文献[10]设计了一类基于脉冲观测器的脉冲控制器；文献[11]对不确定线性系统给出了基于脉冲观测器的镇定方法；文献[12]研究了不确定交换信息的带有脉冲观测器的神经网络的同步；文献[13]研究了基于脉冲观测器的时滞多智能体系统的一致性问题。虽然脉冲观测器的前景较好，但是基于此的多智能体系统一致性控制的相关研究成果仍然较少。

本文旨在设计合适的多智能体脉冲观测器以估计领导者的信息，再根据估计的信息设计相应的控制方法，实现系统的领导跟随一致性。通过构造合适的Lyapunov函数和线性矩阵不等式理论，给出了系统实现领导跟随一致性的充分条件。

1 预备知识及问题描述

1.1 图论

多智能体系统可用有向图M(A)=(V,E,A)表示，其中V={s1,s2,···,sN}表示多智能体系统节点的集合，E={ei j=(si,sj)}⊂V×V描述智能体之间的连接关系。L=[lij]N×N表示多智能体的邻接矩阵。如果(si,sj)∈E， 则lij>0， 否则lij=0。对具有领导者的多智能体系统，令H=L+D， 其中D=diag(d1,d2,···,dN)∈RN×N表示领导者和跟随者之间的连接矩阵，di(i=1,2,···,N)表示领导者与跟随者之间边的权值，跟随者接收领导者发送的状态信息时di>0， 否则di=0。在有向图M中，若某个节点到其他任何节点都存在路径连接，则称图M具有一棵以该节点为根节点的有向生成树。

1.2 模型

考虑具有一个领导者和N个跟随者的领导跟随多智能体系统，该领导者的动态方程描述为

式中：x0(t)∈Rn为领导者的状态信息；y0(t)∈Rp和u0(t)∈Rm分别为领导者的输出和输入信息。此外，跟随者i=1,2,···,N的动态方程为

式中：xi(t)∈Rn为跟随者i的状态；yi(t)∈Rp和ui(t)∈Rm分别为跟随者i的输出和输入信息。

令序列 {tk} 为本文的采样序列，该序列满足0 ≤跟随者都能估计得到领导者的状态信息，设计脉冲为了让所有全维观测器为

式中：K∈Rm×n为系统(2) 的控制增益矩阵。

定义 εi(t)=xi(t)-x0(t)为 跟随者i对领导者的追踪误差；ei(t)=xˆi(t)-x0(t) 为 跟随者i对领导者状态的观测误差。结合(1) ～(4) ，可得到误差动力学模型为

此外，基于引理3，上述误差动力学模型可改写为

式中：ε (t) 和e(t)定义分别为

以下是本文所需要用到的定义、引理和假设。

定义1如果对系统(1) ～(2)的任意初始条件，有下式成立：

则称领导跟随多智能体系统(1) ～(2)实现了领导跟随一致。

引理1[14]给定对称矩阵X∈Rn×n，

若X11∈Rr×r，则下列3个条件等价：

(1)X<0；

引理2[15]若矩阵A∈Mn，Mn是n阶实矩阵的集合，那么A的所有特征值满足：

λmin=λ1≤λ2≤···≤λn-1≤λn=λmax

则对任意x∈Rn，有λ1xTx≤xTAx≤λnxTx。

引理3[16]符号“ ⊗”表示kronecker积。对任意a∈R 和矩阵A、B、C、D，有下列运算性质：

(1) (aA)⊗B=A⊗(aB);

(2) (A+B)⊗C=A⊗C+B⊗C;

(3) (A⊗B)(C⊗D)=(AC)⊗(BD);

(4) (A⊗B)T=AT⊗BT。

假设1(A,B,C)是可镇定和可观测的。

假设2领导跟随多智能体系统的通信拓扑具有一棵以领导者为根节点的有向生成树。

2 主要结果

本节定义了一个分段连续函数ϕ (t)，并在此基础上构造了分段Lyapunov函数，利用LMI技术给出了误差动力系统(6)实现指数稳定的充分条件，即系统(1) ～(2)实现了领导跟随一致性。

定义函数：

和分段连续函数

则对任意t∈[tk,tk+1),有

式中：h≤infk∈N{tk+1-tk}，c>0， µ ≥1，k∈N。

定理1在假设1和2成立的情况下，如果存在c>0 ，µ ≥1，δ0<0 ，h≤infk∈N{tk+1-tk} 和 正定 矩 阵P1，P2，W1，W2，使下述不等式成立。

则多智能体系统(1) ～(2)在脉冲观测器(3)和控制器(4)的作用下实现了领导跟随一致。

证明选取Lyapunov函数：

即对任意t=tk,∀k∈N，有

另一方面，当t∈(tk,tk+1)时,

即有式(17)成立。由式(14) ～(17) ，通过数学归纳法可得，对任意t∈[tk,tk+1)， 有V(t)≤λ2||η(t0)||2eδ0t成立。由于δ0<0 ， 故当t→∞时 ，有V(t)→0，即误差动力学系统(6)在脉冲观测器(3)和控制器(4)的作用下可实现指数稳定，证毕。

注解1与文献[10]中单个系统的分析不同，本文为基于网络交流的智能体系统的协同控制提供了一种有效的方案。

注解2在多智能体系统的实际应用中，基于连续测量的观测器会造成较高的资源负载[6-7]。为了克服这一缺点，脉冲技术被采纳到观测器的设计中。脉冲观测器有效地减少了智能体间的通信负担，因为该观测器只需要智能体在t=tk时刻与其相邻智能体交换信息并更新相应的一致性协议。而在脉冲时刻之间，即任意t∈(tk,tk+1),∀k∈N，脉冲观测器将仅仅依赖自身的动力学运行。在此u0=0过程中，其通信资源的占用率几乎为零。

定理1是在假设矩阵K和G已知的情况下得到的。如果这些矩阵事先不可得知，则难以应用该定理。对此，本文给出定理2。该定理可设计合适的矩阵K和G，并基于脉冲观测器(3)与控制器(4)，实现多智能体系统(1) ～(2)领导跟随一致。

定理2在假设1和2成立的情况下，如果存在µ≥1,c>0,δ0<0，h≤infk∈N{tk+1-tk} ，正定矩阵X，P2，W1，W¯1，W2，以及矩阵Y，Z，使得下述不等式成立：

则多智能体系统(1) ～(2) 在脉冲观测器(3) 和控制器(4) 的作用下可实现领导跟随一致。

另外，令Z=GTP2，则由式(18)可得式(10)。因此，通过定理1可知，多智能体系统(1) ～(2)在脉冲观测器的作用下可实现领导跟随一致。证毕。

3 数值算例

考虑3个跟随者和1个领导者组成的线性多智能体系统，其拓扑图如图1所示。

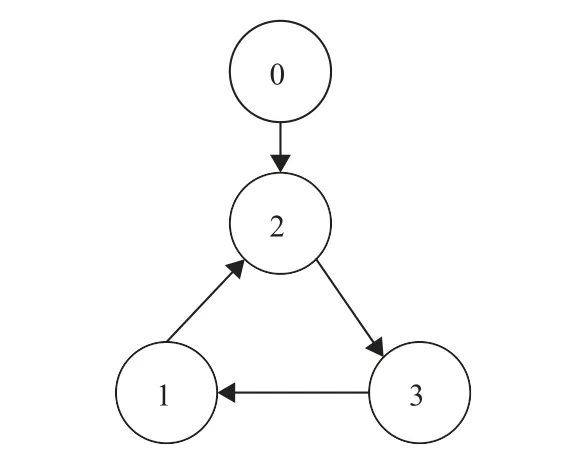
图1 线性多智能体系统拓扑图Fig.1 Topology of the linear multi-agent system

由图1可知，Laplacian矩阵L及连接矩阵D为

则有

各智能体状态初值在[-5,5]内随机选取，系统参数为

选择c=10, µ=1.05,h=1，用MATLAB中LMI工具箱求解式(18) ～(19)的可行解，得到

另外，由K=YX-1和G=P2-1ZT分别可知

假设脉冲观测器的观测频率是周期的，tk+1-tk≡1，得到的仿真图如图2～5所示。

图2 观测误差e i1=xi1-x01 (t k+1-tk ≡1)Fig.2 The observaion error e i1=xi1-x01 (t k+1-tk ≡1)

图3 观测误差e i2=xi2-x02 (t k+1-tk ≡1)Fig.3 The observaion error e i2=xi2-x02 (t k+1-tk ≡1)

图4 追踪误差 ε 1=x1-x0 (t k+1-tk ≡1)Fig.4 The tracking error ε 1=x1-x0 (t k+1-tk ≡1)

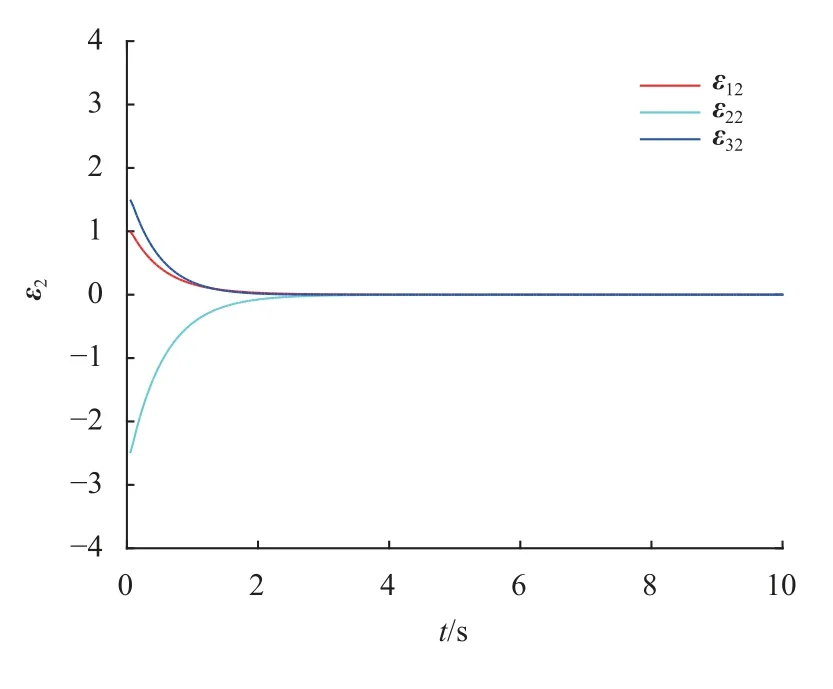
图5 追踪误差ε 2=x2-x0(t k+1-tk ≡1)Fig.5 The tracking error ε 2=x2-x0(t k+1-tk ≡1)

当tk+1-tk≡1 (此 时h=infk∈N{tk+1-tk}) 时，由图2～5可知，观测误差收敛，所设计的脉冲观测器可以准确观测领导者信息，多智能体系统可以实现领导跟随一致。

4 结论

本文设计了可估计领导者状态的脉冲全维观测器，并在此基础上解决了领导跟随一致性问题，利用分段Lyapunov函数和线性矩阵不等式理论，给出了跟随者准确估计领导者状态且系统实现领导跟随一致性的条件。未来，将对事件触发脉冲观测器进行深入研究。