基于互补集合经验模态分解与样本熵算法的接地系统故障选线研究
马 超,林 希,刘振祥
(1.广东电网有限责任公司 江门供电局, 广东 江门 529000;2.广州思泰信息技术有限公司, 广东 广州 510006)
从现场运行情况来看,配电网中发生的单相接地故障数量占总故障类型的80%以上[1],而我国配电网系统中广泛采用中性点经消弧线圈接地的接地系统,在发生单相接地故障时消弧线圈的补偿作用会使故障电流减小,特征信息减弱,使得故障线路识别困难,准确率不高[2-8]。
鉴于故障零序电流瞬时响应所持续的时间相对短且含有电流幅值大、频率范围广等丰富的故障信息,因此常被作为故障选线的主要分析对象[9]。专家学者针对故障的零序暂态电流含有大量高频分量的特点,提出许多故障选线新方法。文献[10]通过研究正常与故障线路的5、7次谐波分量的波形差异,采用Hausdroff距离得到相对系数,再与阈值比较实现故障选线;但该算法需采集一个周期的电流信号后才能进行算法的分析,识别速度较慢。文献[11] 通过MEEMD分解算法提取并重构信号高频分量的能量、方向等特征量作为GA-AP神经网络的输入向量,进行算法的训练与识别;虽然该算法准确率较高,但由于暂态过程短暂,而神经网络算法所需的算力与时间成本较大,难以应用于工程实际中。文献[12]采用VMD算法分解得到暂态非工频分量,计算分量的整体趋势相关系数矩阵,并应用相关性聚类算法实现故障选线,所提算法具有较好的抗噪性能;但是当消弧线圈的补偿度发生变化时,会影响零序电流暂态特征,可能造成误判。文献[13]采用小波分解对暂态零序电流进行分解得到多个频带信号,再求得各频带的行波能量,通过判断线路的积分比值与阈值的大小实现故障选线,该判据不受系统接地方式和运行状态的影响,具有较高的选线灵敏度;但在实际工程中阈值的设置需要考虑多种参数,整定过程困难。其他采用暂态高频分量作为特征提取的方法,诸如波形比较法[14]、投票法[15]、小波变换法[16-18]等,存在阈值整定困难、小波基函数选取不合适等问题难以应用于工程实际中。因此,亟需一种考虑暂态电流的高频分量特性,实现快速选出故障线路,易于复杂工程场景下可靠应用的故障选线新方法。
针对现有故障选线方法在分析信号长度较长、阈值整定困难、选线准确率低、多场景下快速可靠选线的问题,分析接地故障的零序电流暂态特性,鉴于零序电流高频分量具有震荡和衰减特征等丰富的故障信息,本文提出一种无阈值的基于互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 与样本熵的接地系统单相接地故障选线方法。首先采用CEEMD算法分解得到本征模态函数(Intrinsic Mode Function, IMF) 集合,提取IMF1作为零序暂态故障电流的高频分量,再引入表征序列复杂程度的样本熵原理,选定线路的高频分量样本熵值作为故障选线判据,仿真验证在不同线路故障位置、故障合闸角、接地电阻和消弧线圈补偿度等多场景工况下的应用可行性。
1 零序电流暂态特性分析与表征
1.1 接地故障的零序电流暂态特性分析
中性点经消弧线圈接地系统发生单相接地故障的等效电路如图1所示,其中R0、L0为线路零序等值电阻和线路零序等值电感,RL、L分别为消弧线圈的有功损耗电阻和电感,ud0为故障的零序电动势,Cg为系统等效对地零序电容。
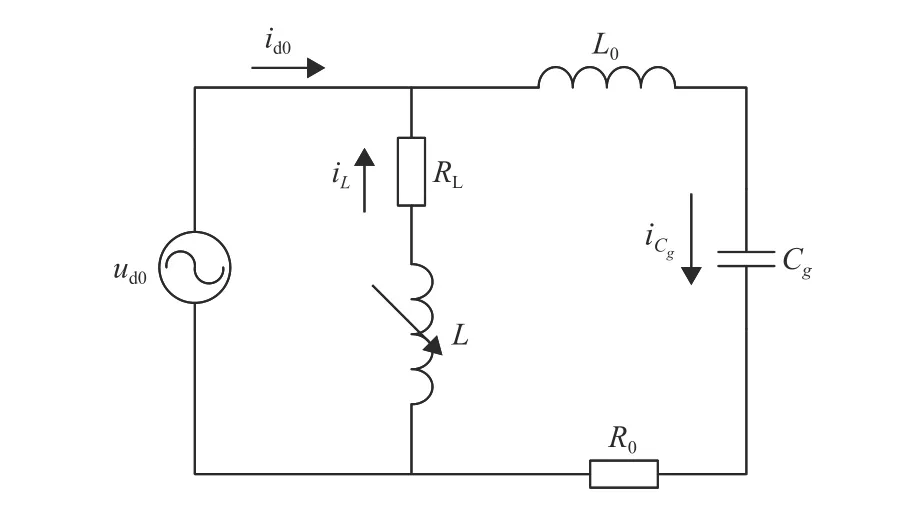
图1 中性点经消弧线圈接地系统单相接地等效零序电路Fig.1 Neutral point through arc suppression coil grounding system single-phase equivalent zero sequence circuit
根据不同回路得到下列微分方程:
式中:Um为接地故障相零序电压幅值,θ 为故障合闸角;iCg、iL分别为暂态电容和电感电流,则接地零序电流id0为
式中:ICM、ILM分别为电容电感电流分量;ωf=为暂态震荡分量的角频率,与系统等效电容、等效电感成反比; µ =1/τC=1/R0Cg为自由震荡的衰减系数, τC为电容电流的衰减时间常数,τL=L/RL为电感支路衰减系数,其中电感支路、电容支路的衰减系数均与系统等效电阻成反比,电感支路的衰减系数与消弧线圈电感成正比,电容支路的衰减系数与等效电容成反比。
由式(2) 可知,零序电流由工频分量与高频分量构成,工频分量是电容与电感电流幅值的稳态分量信号,高频分量由电容电流的暂态震荡分量与电感电流的暂态衰减分量信号组成,其持续时间短,电流幅值大,还具有振荡和衰减的波形特征等特点。如图2所示,当θ=0°时,高频暂态分量最小,工频稳态分量最大;当θ=90°时,高频暂态分量最大,工频稳态分量最小。
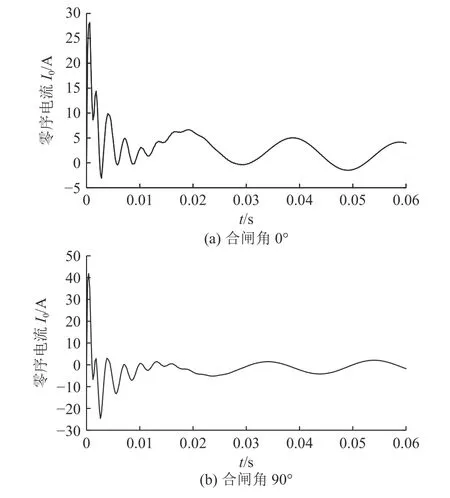
图2 单相接地故障的零序电流Fig.2 Zero-sequence current of single-phase ground fault
1.2 高频分量的提取与表征策略
由于高频暂态分量含有丰富的故障特征信息,本文将高频分量作为主要分析对象。通过对零序电流采用CEEMD算法分解得到IMF集合,然后分析集合内各模态的频域特征;文献[19-20]叙述了零序电流的主要频率范围是300~3 000 Hz。而分解后的IMF1频率区间主要为500~2 500 Hz,如图3所示,在主要频率范围内。因此,提取线路IMF1作为零序电流的高频分量;鉴于高频分量的波形特征复杂,变化趋势不断震荡与衰减,本文采用表征序列复杂程度的样本熵测度方法来表示高频分量的特征信息,通过分析高频分量的复杂特征来实现故障选线,具体选线策略如图4所示。
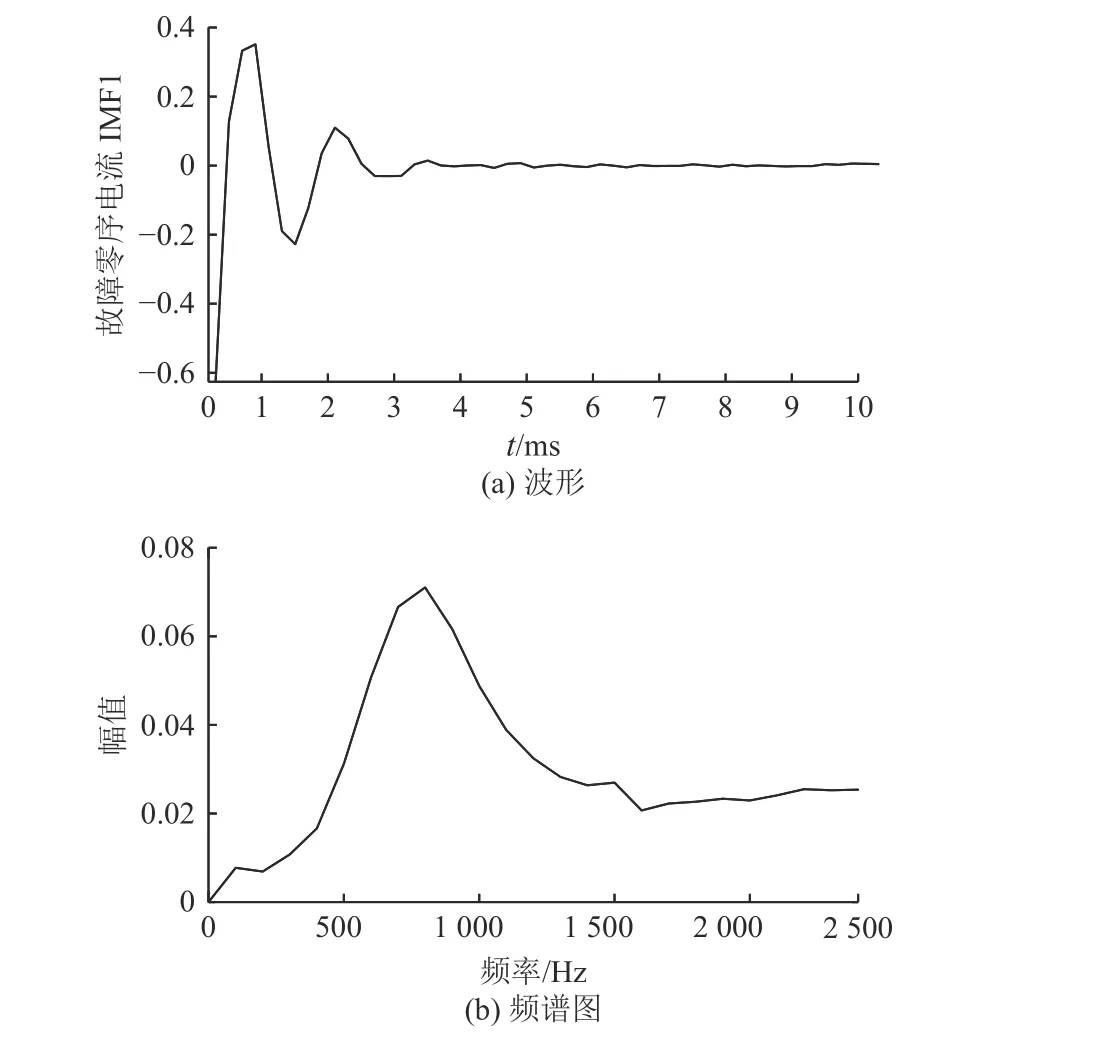
图3 故障零序电流的IMF1波形与频谱图Fig.3 IMF1 waveform and spectrum of fault zero-sequence current
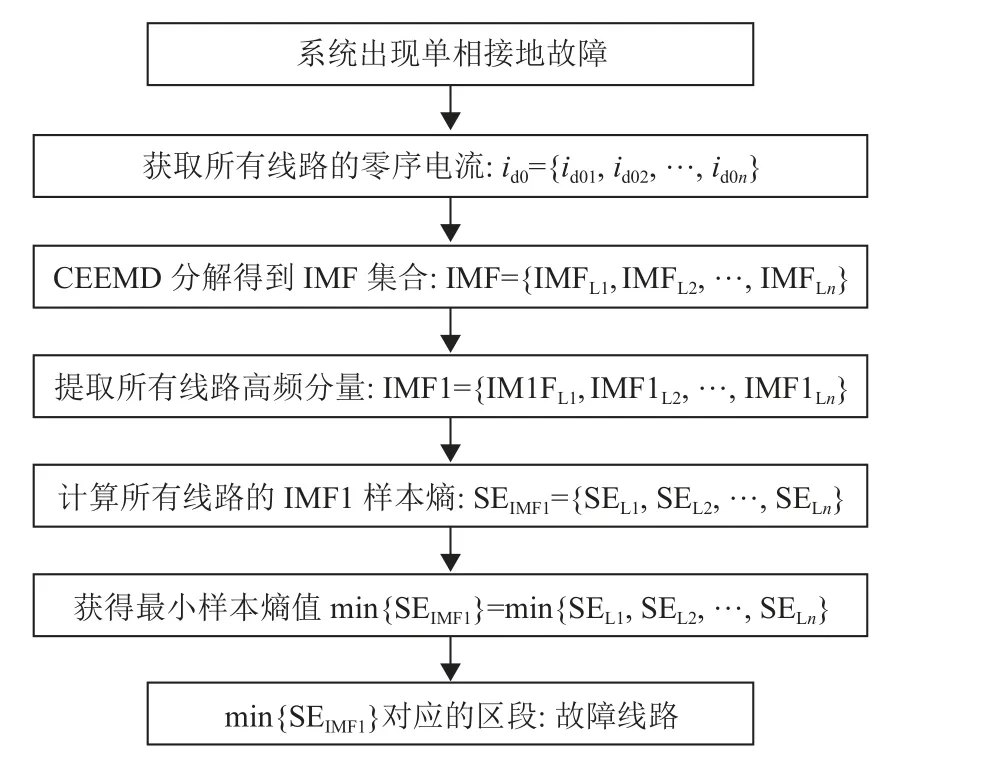
图4 高频分量的提取与表征策略Fig.4 Extraction and characterization strategy of high frequency components
2 故障选线原理及判据分析
为实现对零序电流高频分量的提取,本文采用对非线性平稳信号分解效果更好,模态混叠效应更少的互补集合经验模态分解算法,通过提取分解后的IMF1分量作为高频分量进行特征分析;采用样本熵值来表征高频分量的复杂特征,最后通过比较正常线路与故障线路的IMF1样本熵值的大小,实现快速可靠的故障选线。
2.1 经验模态分解
经验模态分解[21](Empirical Mode Decomposition,EMD) 具有经验、直观和自适应的优点。在处理时间序列问题上,特别适用于对非线性、非平稳数据进行平稳化处理。
EMD能够分解处理任意一种时间序列或信号,但其分解的IMF分量必须满足以下约束条件:(1) 在序列内部,极值点的数量和零点数量保持相同或至多相差一个;(2) 在序列上任意一点,其极大值和极小值确定的上下包络线均值为零。EMD分解步骤如下。
(1) 先根据原始序列x(t)所有极大值点和极小值点求出其上下包络线vup(t)和vlow(t)的 均值m(t)。
(2) 计算原始序列x(t)和m(t)的 差值h(t)。
(3) 若h(t)不符合IMF的条件,重复步骤(1)~(2)直至满足约束条件。若符合,则c1(t)=h(t), 则剩余分量r1(t)为 从原始序列x(t)分 离出c1(t)的结果。
(4) 建立新的序列x(t)=r1(t), 重复以上处理步骤,得到其余的IMF分量和一个剩余分量,EMD的最终分解结果为
式中:n为IMF总数,ci(t) 为 第i个IMF量,rn(t)为余量。
实际情况中,原始信号存在噪声、脉冲干扰等异常情况,造成EMD分解存在模态混叠现象,即一个IMF分量存在多个其他尺度的分量。
2.2 互补集合经验模态分解
针对EMD分解存在模态混叠现象,集合经验模态分解 (Ensemble Empirical Mode Decomposition,EEMD)[22]在整个时频空间多次添加高斯白噪声,然后进行EMD分解,得到多个IMF分量的平均值作为最终的结果。但是EEMD分解结果很难完全消除添加的白噪声,而互补集合经验模态分解(CEEMD)[23-24]通过向时间序列中加入一对正负相反的高斯白噪声可以克服EEMD的缺点。CEEMD的主要原理如下。
(1) 向时间序列加入一对正负相反的随机高斯白噪声。
式中:ni+(t)和ni-(t) 为符号相反的噪声,xi+(t)为时间序列和正噪声总和,xi-(t)为时间序列和负噪声总和。
(2) 通过EMD将xi+(t)和xi-(t)分别分解,得到1组n个子序列分量cij+(t)和cij-(t),则
式中:j为分解后的序号,j=1,···,n。
(3) 重复 (1) ~(2) 步骤k次,得到最终的IMF分量。
经过添加正负白噪声后的CEEMD算法能够有效解决模态混叠效应,降低分解后序列中的残留噪声,从而减少EEMD算法加入噪声对分解结果的影响。
2.3 样本熵
样本熵是一种表征序列复杂程度的测度方法[25],不存在对自身数据的比较而产生计算偏差。序列的自我相似性越高则样本熵值越小,时间序列越复杂则样本熵值越大。具体原理如下。
(1) 序列G={g(1),g(2),···,g(N)},构造m维矢量:
(2)定义G(i)与G(j)间对应元素的距离最大值为d[G(i),G(j)](i不等于j) ,即
(3) 给定阈值r,r= 0.2std,std为序列标准差;统计d[G(i),G(j)] (4) 对上式结果求平均,即 (5) 将维数m加1,重复(1)~(4) 。 (6) 由于实际上N为有限值,则样本熵估计值为 结合CEEMD算法与样本熵原理,得到正常线路与故障线路的高频分量IMF1样本熵值,无需阈值整定,仅比较正常与故障的熵值大小,即可实现故障选线。表1是部分场景下的线路零序电流IMF1样本熵值,设置线路L6发生单相接地故障,其中,θ是故障合闸角,d表示线路发生单相接地故障位置线长占线路全长的百分比,R是接地过渡电阻,单位为Ω,ε为消弧线圈补偿度。 表1 部分场景下的线路零序电流IMF1样本熵值Table 1 Sample entropy value of line zero-sequence current IMF1 under some scenarios 可以看出,不论何种工况下,正常线路的IMF1样本熵皆大于故障线路,因此,仅需寻找IMF1的样本熵最小值,即可确认故障线路。 通过对线路零序电流进行CEEMD分解,提取出零序电流高频暂态分量IMF1作为分析信号,再对各线路的IMF1采用样本熵原理,实现对高频分量的复杂特征表征,最后采用无阈值的选线方法,判断各线路IMF1的样本熵值,最小熵值所对应的线路即为故障线路。具体选线流程如图5所示。 图5 基于CEEMD与样本熵的故障选线方法Fig.5 Fault line selection method based on CEEMD and sample entropy 为验证本文所提故障选线方法的快速性与可靠性,基于simulink仿真平台模拟搭建图6所示的配电网中性点经消弧线圈接地系统模型,共设置6条线路作为分析线路。线路类型为架空线路、电缆线路、架空与电缆混合线路3种类型,各线路长度如图6所示。架空与电缆线路的线路参数如表2所示。架空线路等效零序电感为LJ0=4.6l, 等效零序电阻为RJ0=0.275l;电缆线路等效零序电感为LL0=1.019l,等效零序电阻为RL0=2.7l; 其中l是对应短路线路长度。当线路发生单相接地故障时,可看作在故障位置接入零序电动势ud0,在零序电动势的驱使下,一部分零序电流iL经消弧线圈支路L、RL流入大地,令一部分零序电流iCg经架空线路、电缆线路以及对地电容Cg进行放电,其中线路零序等值电阻、线路零序等值电感为R0、L0。消弧线圈补偿度ε=7%,则电感L的计算公式为 表2 线路参数Table 2 Line parameters 图6 10 kV中性点经消弧线圈接地系统模型Fig.6 Model of 10 kV neutral grounding system through arc suppression coil 式中:CgΣ为系统对地电容总和值,ω为工频角频率,计算得L=0.297 8 H;一般来说,消弧线圈阻抗约为感抗的2.5%~5%,此处取3%,即R=0.03ωL=2.807 Ω。采样频率为5 kHz,分析信号取线路零序电流的半个周期信号。 由零序电流表达式(2) 可知,零序电流与故障发生的位置、故障合闸角、接地电阻和消弧线圈电抗值有重要关联。因此,本文通过模拟发生不同故障距离d、故障合闸角θ、接地过渡电阻R、消弧线圈补偿度ε场景下的单相接地故障,得出多场景工况下的零序电流,并对每条线路应用此选线方法,获得该场景下的高频分量样本熵值,取熵最小值对应的线路进行分析。 由于线路发生单相接地故障的位置变化,会引起零序回路等效电阻的改变,因此,设线路L6发生单相接地故障,其中,R=1 Ω,ε=7%,θ=0°、90°,故障位置线长占线路全长的百分比d为20%,40%,60%,80%。取半个周波的线路零序电流作为分析信号,采用本文所提故障选线方法,算得线路的IMF1样本熵值,整理结果于表3。 表3 不同故障位置的线路零序电流IMF1样本熵值Table 3 Sample entropy values of line zero-sequence current IMF1 at different fault locations 由表3可知,不论单相接地故障发生在线路的哪一位置,本文所提算法皆能在采集半个周期零序电流下完成故障线路的选取。 由零序电流表达式(2) 可知,故障合闸角的大小会影响高频震荡和衰减分量的幅值,因此,设线路L6发生故障,其中,R=1 Ω,ε=7%,故障位置d=20%或60%,合闸相角θ=(0°, 45°,90°,120°) 。取半个周波的线路零序电流作为分析信号,采用本文所提故障选线方法,算得线路的IMF1样本熵值,整理结果于表4。 表4 不同合闸角的线路零序电流IMF1样本熵值Table 4 Sample entropy values of line zero-sequence current IMF1 with different closing angles 由表4可知,在不同故障合闸角情况下,故障线路的高频分量样本熵值都是最小值,因此,本文所提选线方法对不同合闸角具有适应性和可靠性。 实际线路中发生接地会出现多种不同接地电阻场景,继而产生不同幅值与特征的零序电流。因此,假设线路L6发生故障,且θ=90°,d=40%、60%, 接地电阻R=(0.1,1,10,100,1 000) Ω,取半个周波的线路零序电流作为分析信号,采用本文所提故障选线方法,算得线路的IMF1样本熵值,整理结果于表5。 表5 不同接地电阻的线路零序电流IMF1样本熵值Table 5 Sample entropy values of line zero-sequence current IMF1 with different grounding resistances 由表5可知,不论高阻接地还是低阻接地,本文所提选线方法都能通过判断高频分量的样本熵值选出故障线路,其可靠性得到验证。 由第1节可知,消弧线圈的补偿作用可以减小故障电流的稳态幅值,其补偿作用的强弱与补偿度相关。因此,通过设置不同补偿度来验证选线方法的可靠性。将根据式(15) 计算得到补偿度ε取5%和10%情况下的线圈电感与电阻值,以及θ=120°,d=40%参数应用于仿真模型中,对所得数据采用本文选线方法并整理结果于表6。 表6 不同补偿度的线路零序电流IMF1样本熵值Table 6 Sample entropy values of line zero-sequence current IMF1 with different compensation degrees 由表6可知,在不同线圈补偿度场景下,所提选线方法皆能在半个周波电流采集下准确识别出故障线路,其快速性和可靠性得到验证。 针对配电网中性点经消弧线圈接地系统发生单相接地故障概率较高,故障线路的选取存在分析信号时间长、阈值整定困难、选线准确率低等问题,本文分析了单相接地故障条件下的故障零序电流特征,提出基于高频分量波形特征的故障选线模型,得到如下结论。 (1) 提出一种基于CEEMD与样本熵的单相接地故障选线方法,可实现半个周波电流采集下的快速故障选线,且无需阈值整定,易于工程实践应用。 (2) 所提选线方法,能够满足在不同故障位置、合闸角、接地电阻及线圈补偿度等多场景环境下的故障线路选取,模型应用的可靠性较高。 (3) 本文所提出的故障选线方法,能够较好地应用于单相接地故障下的快速选线策略应用;算法的工程应用,需结合具体工况以探究零序故障电流获取的优化,如不对称工况下零序电流的获取及修正。
2.4 基于CEEMD与样本熵的故障选线方法

3 仿真验证


3.1 线路故障位置

3.2 故障合闸角
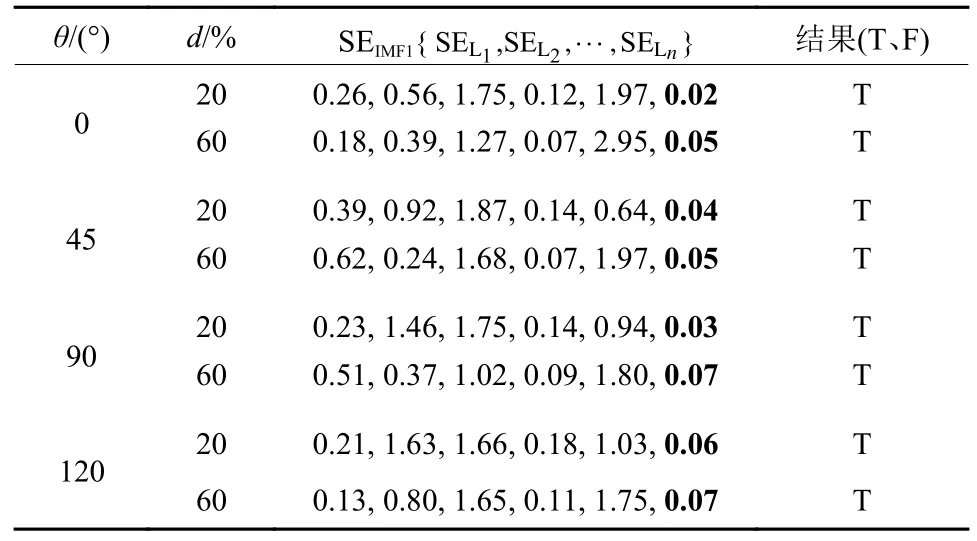
3.3 接地电阻
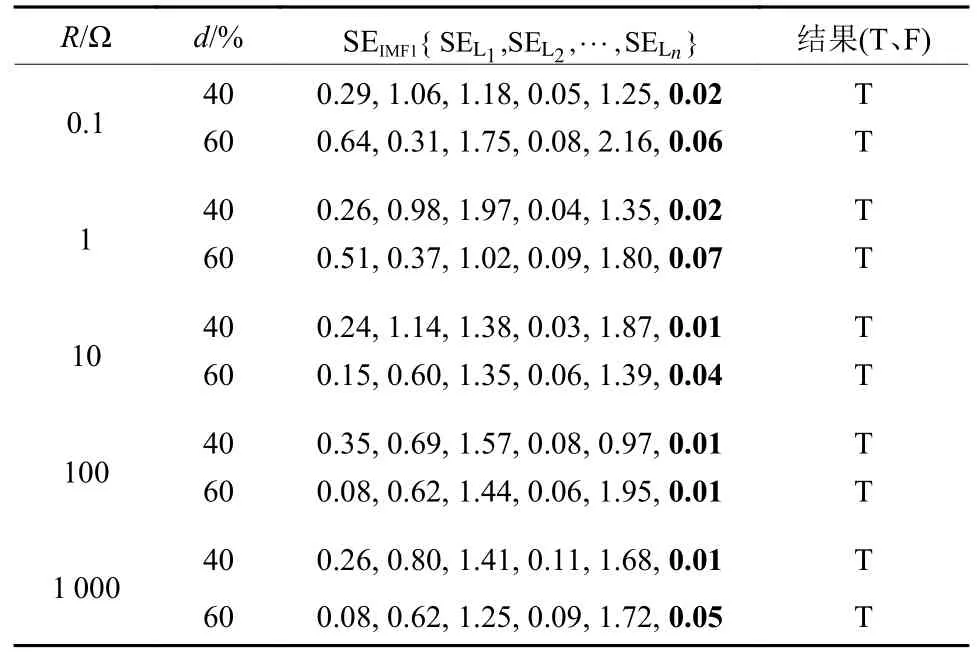
3.4 消弧线圈补偿度
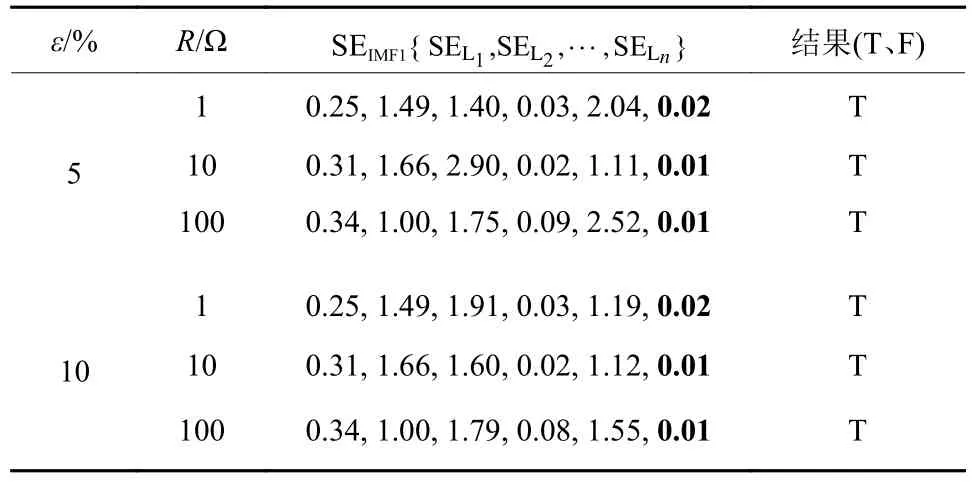
4 结论

