基于SPH 统一框架的流体细节仿真模拟方法∗

华 磊 曾兰玲 杨 洋 赵 岩

（江苏大学计算机科学与通信工程学院 镇江 212000）

1 引言

流体模拟在计算机游戏、电影特效和军事训练等领域有广泛的需求和应用。经过相关学者和专家的不断努力，流体模拟已经取得了很多研究成果，并应用在不同的领域。但是现阶段研究方向都是针对单一流体的仿真模拟，因此如何通过统一框架模拟不同流体的运动状态非常具体挑战性。此外，在具体细节真实感方面，如火焰、烟雾的边缘细节优化还有待进一步提高。

基于粒子的方法［1~3］和基于网格的方法［4］是目前流体模拟最流行的离散化不同层次的典型方案。基于网格的方法假设在无发散条件下具有不可压缩性，在拓扑转换上更有效率，但是无法精确有效的处理场的流动，容易丢失能量和几何合效果。SPH（Smoothed Particle Hydrodynamics）光滑颗粒的流体动力学［5］算法就是典型的拉格朗日粒子法，其基本原理是通过粒子模拟流体的运动规律，然后转换成网格进行流体渲染。如何在计算成本和真实细节之间做出的合理的选择是目前流体模拟的研究热点［6~10］，但该方面的工作基于的都是单一的流体性能方面的模拟。其中文献［11~14］的研究工作是采用预先存储的数据，通过不同状态的组合生成最后的效果，文献［15］是通过加快邻域粒子的搜索速度来提高计算机模拟性能。针对多样化流体模拟研究方面的工作较少，因此，实现多样化流体模拟的统一框架具有实际应用意义。

由于SPH 可以有效地表示小的液体特性与低内存成本等特点，本文研究如何利用SPH来实行多样化的流体效果，并通过SPH中的光滑核函数的优化，实现一个控制流体多样化的统一框架。细节模拟方面，由于SPH 对粒子分布很敏感，在实现水波纹和烟雾波动等细节效果，可以选择在边界层粒子的位置进行细节化处理。目前的相关研究工作主要采用毛细管波和重力波模拟流体中的波纹细节效果，但毛细管波速度快、高频率难以模拟，而重力波在细节处理方粗糙，因此，文献［16~17］研究在虚拟环境中模拟声波的传播。由于声波速度快，可以在流体的表面模拟声波，且不存在数值化问题等优点，本文采用声波，即压缩波对流体边界层细节进行优化处理。该工作背后的基本思想是基于SPH结合声波的方法，实现丰富多样化的3D 流体细节效果。

2 相关工作

流体模拟一直以来都是大规模图形模拟的重点研究方向，到目前为止，已经提出了许多流体模拟方法，并取得比较真实的结果。

SPH 是一种流体模拟算法，相对于其它的模拟算法，其特点就是简单快速，是典型的拉格朗日视角，它的基本原理就是通过粒子模拟流体的运动规律，可以有效地模拟小尺度的流体运动。

现阶段在SPH 上的主要研究工作是实现实时SPH 流体模拟，主要采用并行加速计算方法。SPH在模拟各种流体效果的应用方面也取得了很多成果，如水体［18］、多相流体［19］和固液耦合［20］。Amada，et al［21］首次提出了基于图形处理器的SPH 流体模拟，该方法在中央处理器上执行最近邻域搜索（Nearest Neighbor Search），并在图形处理器上求解N-S方程，以加速流体模拟。之后，Harada，et al［22］、Zhang，et al［23］将除渲染场景之外的所有步骤都放在GPU上，进一步提高了流体模拟的效率。

现实生活中的很多流体边界层现象不能用单相流体来模拟，多流体模拟是解决这一现象的关键。Müller，et al［24］首先引入体积分数的概念来表示不相同的空间分布，实现混合流体的多流体模拟系统。Kim［25］、Misztal，et al［26］采用网格的方法，并假设混合流体不可压缩且不发散情况下，该方法在拓扑转换上获得较好的结果。面对混合现象由浓度差引起的扩散效应，Liu，et al［27］引入了一种新的多流体模拟方法，该方法能够真实地捕捉由于多种流体之间的相对运动、湍流相互作用和力变化分布而导致的复杂混合现象。湍流相互作用和力变化分布而导致的复杂混合现象。

目前，主流方法是基于SPH的表面张力来优化流体的边界层模拟效果。早期工作大多集中在连续体表面力CSF（Continuum Surface Force）方法上。CSF 的主要缺点是在自由表面情况下严重依赖粒子样本。如果没有足够的粒子，会导致模拟结果数值不稳定性和不准确性的问题。此外，He等［28］提出在微水平上将表面张力模拟为粒子之间的分子力方法，实现流体边界模拟。最近，何小伟等［29］提出一种新的表面张力模型，该模型是基于扩散界面方法处理稀疏采样的自由表面。与其它表面张力相比，毛细管波尤其难以模拟，因为该方法需要一致和准确的表面张力估计。

综上，本文提出基于SPH 算法，并结合压缩波进行边界层细节优化的方法实现多流体细节模拟。

3 算法实现

论文算法方案结构如图1 所示。算法流程如下。

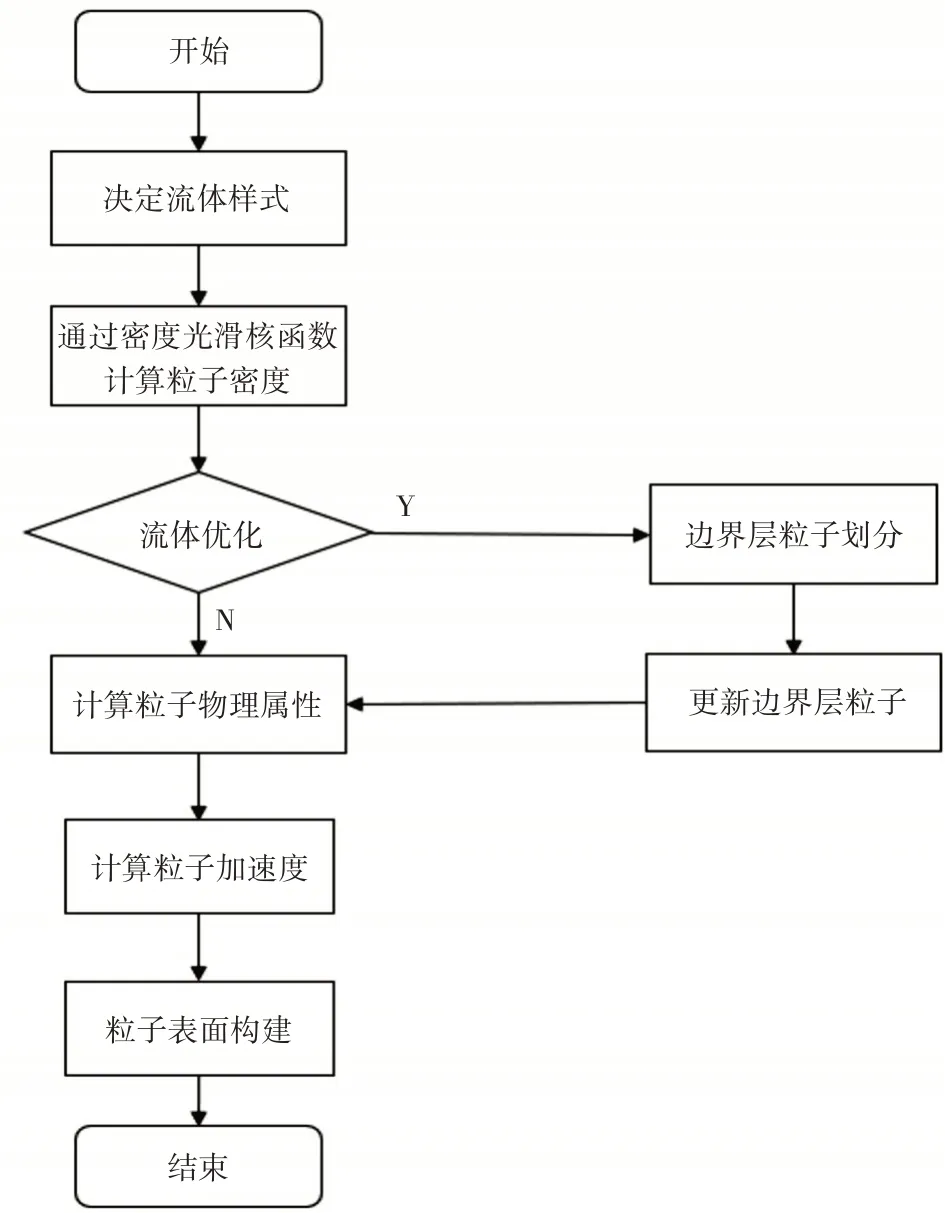
图1 整体算法结构

第一步：确定所要模拟的流体属性，选择本文优化的密度光滑核函数对应的属性因子m；

第二步：光滑核函数代入到SPH 算法，求得粒子的密度；

第三步：是否选择优化流体效果，如果选择Y进入到第四步；否则直接进入到第六步；

第四步：通过流体的边界层进行边界层粒子划分；第五步：通过声波公式求出代更新的边界层密度；第六步：进行粒子的初始化求粒子的物理属性（例如重力、粘滞力等），得出粒子的加速度；

第七步：通过MC 算法进行流体表面构建得到想要的流体模拟效果。

3.1 SPH等式

SPH 是最流行的拉格朗日方法。它能有效地模拟小尺度自由表面流体。不可压缩牛顿流体的运动由N-S 方程描述，而SPH 方法中选取简易的N-S 方程，分析得出作用在一个微粒上的作用力由三部分组成，如式（1）所示：

其中称为外部力，一般就是重力，如式（2）所示：

是由流体内部的压力差产生的作用力，如式（3）所示：

是由粒子间的速度差引起的，跟流体的黏度系数以及速度差有关，如式（4）所示：

根据式（2）~式（4）带入到式（1），并带入公式，可以得到：

加速度则为

以上就是粒子运动学的计算方法，其中u 表示速度，ρ表示密度，p 表示压力，g 为重力表示外力，μ表示粘度系数。

SPH 算法与其他的流体力学中的数学方法类似，同样涉及到“光滑核”的概念，因为流体中每个位置参与运算的值都是由周围一组粒子累加起来的，则该处某项属性Attribute 的累加公式，如式（7）所示：

其中Attributej是要累加的某种属性，mj和ρj是周围粒子j的质量和密度，和是粒子i 和j的位置，h是光滑核半径，而W就是光滑函数。

求解N-S 方程需要满足动量守恒和质量守恒。由于SPH粒子的数量在产生后不会发生变化，所以SPH中的粒子i在其运动过程中可以满足质量守恒。SPH粒子i的加速度可以由式（5）计算得出：

其中Fi是等式（1）外力之和。ai为本文更新粒子i的位置的加速度，推算得到的加速度公式如式（6）所示。

3.2 基于SPH的优化

由于基于SPH 的原始方法以及扩展方法都无法实现一个统一的流体控制框架，针对这个问题，本文对SPH的光滑核函数进行优化，计算粒子密度的光滑核函数可以改写成式（9）所示：

接下来根据式（7），用ρ代替Attribute 可以得到式（10）：

计算密度中将不再使用之前光滑核函数称为Poly6 的光滑核函数，而是使用式（9）。现将其带入到式（10）中，则处的密度计算公式最终为式（11）：

根据式（7），压力计算中使用的光滑核函数称为Spiky 函数，因此在ri处由压力产生的加速度部分为式（12）所示：

根据式（7），粘滞力计算中使用的光滑核函数称为Wviscosity，在ri处由粘滞力产生的加速度部分为式（13）所示：

将式（12）、式（13）代入到公式中得到式（14）所示：

通过修改本文采用的密度光滑核函数参数，对基本的流体仿真模型进行复杂形变，包括流体（火、烟）抖动形变和流体溅落形变。对基本流体仿真模型进行的复杂形变通过修改密度光滑核函数中的属性因子m、分母系数k 实现，在可控区域内，m=1、0.5、h（核半径）是最接近现实流体的仿真构建，粒子显示结果如图2所示。

图2 统一框架呈现的粒子效果雏形

3.3 基于声波的细节处理

本文在流体仿真细节优化处理中，使用声波的波动方程来更新密度变化，如式（15）所示：

其中c为波速，ρouter表示流体表面边界层中的粒子关于位置x和时间t的波强度的一个测量。

式（16）所示，其中γ是表面张力，k 是波数，ρ0的流体密度。对于水，论文使用ρ0=1.0*103kg/m3，对于气体相对应的可以直接使用空气的密度ρ0=1.293 kg/m3。

尽管声波和水体的毛细管波虽然很多的行为相似，但是还有一定的区别：液体毛细管波只在表面传播，声波可以在液体的体积内传播。如果只是简单地求解式（16），模拟流体会得到不一样的模拟效果，尤其在模拟流体的粒子数目过多的情况下。为了实现更加逼真效果，针对上述问题，论文采用的解决方案是检测流体表面边界层的粒子，并对粒子进行范围的划分，让声波在不同边界层范围内进行传播，该方法可以实现较好的流体细节效果。因此，本文引入了流体的边界层划分算法，如式（17）所示：

其中式（17）表示布拉修斯对平板层流边界层求得的精确解，其中v 表示运动粘度，v∞表示的是主体流速，δ表示的是边界层厚度，边界层厚度指的就是壁面到流速与主体流速v∞相差不到1%的流体层厚度，如式（18）所示：

其中μ表示流体的动力粘度（粘性的度量，也称粘性系数），ρ表示液体密度。

根据式（14），可以求得每个粒子的加速度情况，因为速度是矢量，那么主流体的速度，如式（19）所示：

其中公式t表示时间，n表示粒子数。

如图3 所示，接下来就是将式（19）中得到的主流体流速代入到式（17）中，得到了流体的边界层，将式（16）带入到式（15）可以得到ρouter，更新边界层中粒子的密度为ρouter。就可以将声波形成的细节效果带入到流体的表面。以水流为例，实现效果与没有声波丰富细节明显的区别如图4 所示，对比效果，图（a）细节化程度明显弱于图（b）采用的本文方法。且图（a）中文献［30］的实现方法需要构造一个密集的点集的拓扑变化，添加了算法的复杂度，因此本文中的方法更加容易实现。

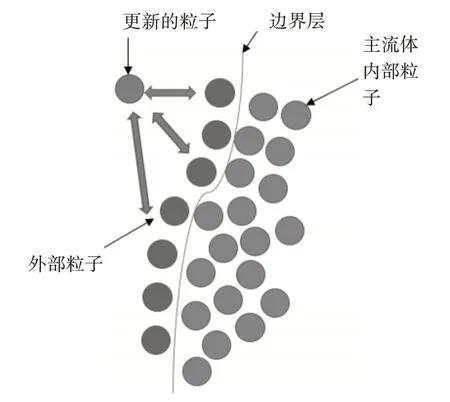
图3 边界层粒子划分

图4 （a）（b）表面波纹对比

为了进一步验证本文细节优化处理的有效性，通过粒子实验来进行验证，计算参数有：流体初始密度为ρ=1000kg/m3，流体模拟粒子数为2200 个，边界粒子数为120 个，粒子影响半径r=0.02m。从图5 中可以看出，在其他条件相同的情况下，图（a）相对图（b）的流体表面均匀，图（b）的凹凸效果更加明显，因此本文方法可以提高流体表面细节仿真效果。

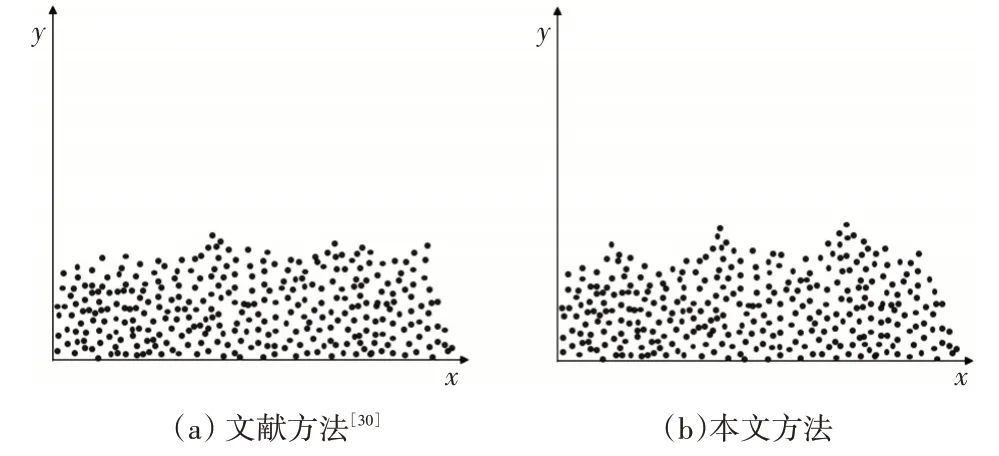
图5 粒子方法对比

4 实验结果

本文实验是在一台配备英特尔酷睿i7-8700K 3.70GHz、英伟达GTX1080 显卡、16G 内存，操作系统为Windows 10 的电脑上测试文中的算法。整个实现基于OpenGL，使用的是MC 算法（Marching Cube Algorithm）进行流体液面绘制。这里给出了一些实验结果，这些结果显示了本文所提出的方法的有效性。经过实验不仅完成了整个基于物理的流体方程的推导，同时也将计算的结果实时绘制出来。

实验结果验证了本文算法所对产生丰富的细节多样化流体效果，论文中的实验例子包括多样化的流体雏形效果（如图2），图2 的实验得到了一个基于SPH 不局限单一流体的框架。在图2 多样化的流体雏形的框架基础上，添加粒子数，为粒子添加对应流体的颜色，结合MC 的流体表面绘制，呈现小型流体波纹效果（如图3），火焰燃烧（图6）的流体效果，以及烟雾吹动的效果（图7）。这些例子说明了本文算法的正确性，以及类似现实世界中的流体的波动效果。在图5 中，文中方法（图（b）、（c））比较Müller's（图（a））的方法在火焰上实现的对比，可以看出文中的方法优化流体细节方向这一块，使得流体显示的效果更加鳞次栉比。经过图7的实验，图（a）是将何晓伟等［30］实现毛细管波的方法来丰富烟雾的细节化，效果是近似现实效果，但计算时间长，图（b）、（c）实验展示本文的方法应用到烟雾模拟中的，图（b）中粒子细节效果更加丰富，再进行表面绘制得到的图（c）的结果，经过实现得到近似现实世界烟雾效果，在烟雾刚开始的起始阶段基于文中算法得到的细节效果好于文献［30］的方法。

图6 丰富的细节化火焰

图7 丰富的细节化烟雾

由表1~2 中的数据结合图5 和图7 的模拟效果可以得出在相同的条件下，随着时间的增加，本文的最高速度与最低速度差明显大于Müller's的方法和文献［30］的方法，进一步得出本文方法速度波动大，流体模拟细节越显著。

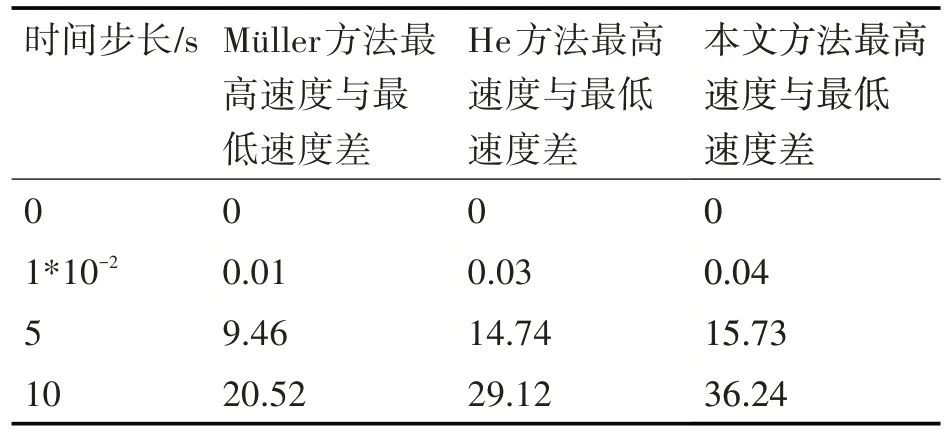
表1 N=45000数据

表2 N=70000数据

本文采用的算法实现多样化的流体效果，是局限小型流体，大型流体的效果会出现过度偏差细节化优化也会出现失真的效果，并且流体运动过长，细节方面也会出现精度问题。算法在细节优化步骤上是基于压缩波的，相对于液体的毛细管波等现实波纹细节方面，并不意味着物理上的精确。文中算法不指定流体的具体密度，是根据单一的密度来实现多样化的流体细节优化的效果。最后，基于文中算法的基础得到的结果在某种程度上是取决于表面的粒子颗粒上的。

5 结语

论文提出了一种框架，基于SPH实现丰富细节的多样化的流体模拟。基于SPH 的基础下优化光滑核函数实现了多样化的流体框架不再局限于单一的流体模拟，并且结合声波实现细节优化的方法。经过实验，表明了这是一个合理的假设。经过实验研究进一步表明了，在SPH框架声波更新的表面粒子可以为优化流体的细节提供很好的方向。

本文中的方法可以实现多样化的流体模拟，但是将该方法应用于大型流体模拟是我进一步研究的工作。另外，在未来，希望基于以上算法的基础，进行理论的研究，实现多种多样流体控制。并且想进一步研究气液耦合方面的压强问题，以获得更精确的细节优化效果。更进一步的话，将通过机器学习来提高文中算法的性能，提高整体算法的模拟速度。