三角函数最值问题的求解策略

孙 婷

(山东省枣庄市第三中学)

三角函数的最值是三角函数的重要性质之一,也是高考命题的热点.随着新课标理念的不断深入,相关试题也在发生变化,但万变不离其宗,只要熟练掌握解题方法,我们定能“驰骋”考场.

1 利用合一变换求最值

所谓合一变换,就是利用三角恒等变换公式将题目给出的表达式变形成y＝Asin(ωx＋φ)(A＞0,ω＞0),然后再求该函数在给定区间上的最值.这种题型是高考关于三角函数最值的主要题型,重点考查三角函数恒等变换的技巧和三角函数的性质.

本题考查二倍角公式和辅助角公式的应用,利用合一变换将函数化成y＝Asin(ωx＋φ)(A＞0,ω＞0)的形式,再利用三角函数的性质求解.

2 利用换元法转化为二次函数求最值

当给出的三角函数解析式中既含有sinx,又含有cosx,且它们的次数既有一次型,又有二次型时,我们一般采用换元法,结合同角三角函数的平方关系将原函数转化为有限区间上的二次函数的值域问题.

例2 求函数f(θ)＝|sinθ－a|－cos2θ(a∈R)的最小值.

本例将三角函数的最值问题与含参二次函数的最值问题交会,考查考生的知识应用能力和分类讨论思想,具有一定的难度.

3 利用导数工具求最值

当题目中出现的三角函数名不统一,次幂也不统一时,一般可考虑利用导数工具来求解.利用导数工具求三角函数最值问题难度不大,体现了三角函数命题的新方向.

例3 如图1所示,有一景区的平面图是一半圆形,其中直径AB长为2km,C和D两点在半圆弧上,满足BC＝CD,设

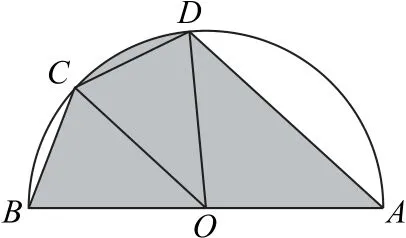
图1

(1)现要在景区内铺设一条观光道路,由线段AB,BC,CD和DA组成,则当θ为何值时,观光道路的总长l最长,并求l的最大值;

(2)若要在景区内种植鲜花,其中在△AOD和△BOC内种满鲜花,在扇形COD内种一半面积的鲜花,则当θ为何值时,鲜花种植面积S最大?

(1)如图2 所示,取BC的中点M,AD的中点N,连接OM,ON,由垂径定理可得OM⊥BC,ON⊥AD,又,所以

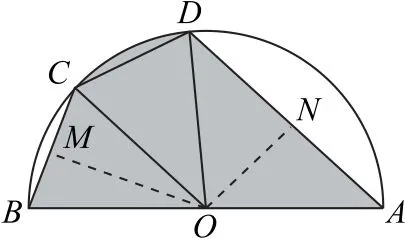
图2

本例第(1)问采用了配方法求三角函数的最值;本例第(2)问采用导数法求三角函数的最值.利用导数法求最值常出现在最优化问题中,实际上是考查三角函数与导数的综合应用,考查考生的数学建模素养和数学运算素养.

当然,求解三角函数最值问题有时会用到基本不等式或通过构造几何图形来处理,但上述几种方法比较常见,同学们应牢固掌握.

(完)