与三角形相关的实际应用问题

王化生

(山东省济南市章丘区第五中学)

处理与三角形有关的实际应用问题,往往需要灵活运用解三角形、三角函数、导数、基本不等式等知识进行综合分析.此类问题考查了学生对相关数学知识、方法的综合运用能力,同时也充分体现了数学的应用价值,有利于培养学生的直观想象、数学运算以及数学建模核心素养.

1 借助三角函数或基本不等式巧解应用题

例1 如图1 所示,某市拟建立一文化休闲公园,该公园为五边形区域ABCDE,其中三角形区域ABE为红色文化游览区,四边形区域BCDE为健身休闲区,AB,BC,CD,DE,EA,BE为文化休闲公园的主要道路(宽度忽略不计),∠BCD＝∠CDE＝120°,∠BAE＝60°,DE＝3BC＝3CD＝3km.

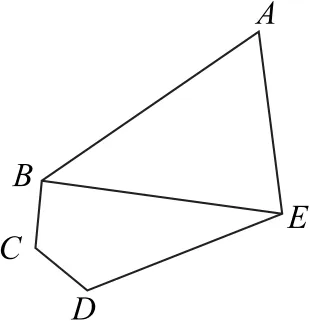
图1

(1)求BE的长度;

(2)求AB＋AE的最大值.

(1)连接BD,在△BCD中,由余弦定理得

因为BC＝CD,∠BCD＝120°,所以

又∠CDE＝120°,所以∠BDE＝90°,故

(2)方法1 设∠ABE＝α,因为∠BAE＝60°,所以∠AEB＝120°－α.在△ABE中,由正弦定理得

所以AB＝4sin(120°－α),AE＝4sinα,从而可得

易知0°＜α＜120°,所以30°＜α＋30°＜150°,则当α＋30°＝90°,即α＝60°时,等号成立,故AB＋AE的最大值为.

方法2 在△ABE中,由余弦定理得BE2＝AB2＋AE2－2AB•AEcos∠BAE,又BE＝2 3,∠BAE＝60°,所以

本题第(1)问较简单,第(2)问具有一定的难度,方法1运用了正弦定理与三角函数知识进行求解,解题过程较为烦琐;方法2综合运用余弦定理与基本不等式的变形结论加以求解,过程较为简洁.

2 借助导数巧解应用题

例2 如图2所示,某城市有一块边长为2km的菱形状绿化区ABCD,其中BMN是半径为1km的扇形,.管理部门欲在该地从M➝P➝Q➝D修建小路:在上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ.问:点P选择在何处时,才能使得修建的小路?,PQ与QD的总长最小?并说明理由.

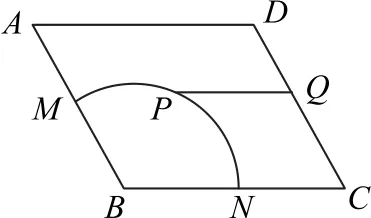
图2

连接BP,过P作PP1⊥BC于点P1,过Q作QQ1⊥BC于点Q1.

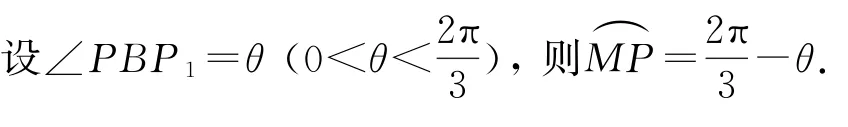
本题具有较强的综合性,解题的关键步骤如下:一是在“设元”(即引入辅助角)的基础上,结合图形得到修建的小路总长的函数表达式;二是灵活运用导数与三角函数知识求解函数的最小值点.从整体上看,本题设计较好,充分体现了函数、导数以及三角函数等知识在解决实际问题中的综合运用.

3 借助基本不等式和导数巧解应用题

例3 如图3 所示,太湖一个角形湖湾AOB,∠AOB＝2θ(常数θ为锐角).拟用长度为l(l为常数)的围网围成一个养殖区,有以下两种方案可供选择:

图3

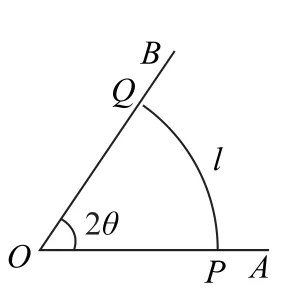
图4

方案二:如图5 所示,围成三角形养殖区,其中CD的长度为l.

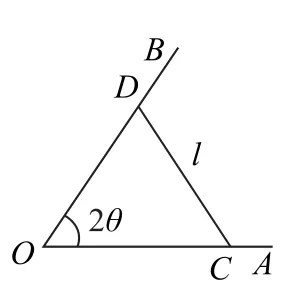
图5

(1)求方案一中养殖区的面积S1;

(2)求方案二中养殖区的最大面积S2;

(3)为使养殖区的面积最大,应选择何种方案?并说明理由.

解题难点:一是综合运用解三角形与基本不等式知识巧求方案二中养殖区的最大面积;二是在“作差”的基础上,灵活构造函数,借助导数知识巧妙地比较S1与S2的大小.由于第(3)问可以看作是北师大版教材«数学必修4»第40页习题B 组习题结论“若x为锐角,则sinx＜x＜tanx”在解题中的灵活运用,所以该题源于教材,故应引起我们的重视.

(完)