松散润叶筒三维传热传质过程数值模拟

沈凯,潘凡达,李旭,樊虎,徐超,韩玉峰,詹望成,金浩

1.浙江中烟工业有限责任公司 技术中心,浙江 杭州 310024;2.华东理工大学 化学工程系,上海 200237

0 引言

松散润叶筒是制丝生产过程中的关键设备之一,通过对运输、储存后的干燥烟叶进行加温、加湿、松散,提高其韧性和耐加工性,对最终卷烟成品的品质具有重要影响[1-2]。

目前烟草行业内对润叶工序的研究主要集中在其对烟叶常规化学、致香成分和感官品质的影响[3-5],对于松散润叶机的研究主要集中于设备改进、工艺精准控制及筒内烟叶的运动轨迹等。靳毅等[6]建立了PID反馈控制模型,根据目标偏差值调节烟叶流量,实现了对出口含水率的反馈控制,提高了各批次松散回潮的均匀性;周群华等[7]在循环热风旁通管路上安装角行程执行器,使热风温度过程控制CPK值达到更高标准;张天驿等[8]提出了一种基于红外图像边缘检测对润叶过程中烟叶运动轨迹的分析方法,拍摄了烟叶瞬态和轨迹图像;刘栋等[9]以CO2膨胀烟丝为示踪物,运用负阶跃示踪法研究滚筒内烟丝停留时间分布情况;周凯敏等[10]提出一种滚筒烘丝机内烟丝滞留时间数学模型,并利用离散元数值仿真模拟研究各工艺参数对滞留时间的影响,得出不同工艺条件对烟丝滞留时间的影响大小依次为倾角>半径>转速>长度>风速。

目前,涉及松散润叶筒内热量和质量传递的数值模拟研究鲜有报道。鉴于此,本文拟采用Euler/Euler/Lagrange模型[11]模拟气液固多相湍流流动,在Euler坐标系中考查气固两相运动,在Lagrange坐标系中考查喷雾液滴运动[12],研究筒体倾角和喷雾喷射角对松散润叶筒内部温度和烟叶含水率分布的影响,以期为松散润叶设备改进和优化操作提供理论参考。

1 数学模型的建立

1.1 几何模型

松散润叶筒主要由进料口、筒体、抄板、喷雾、出料罩等部分组成,数值模拟过程中所用的松散润叶筒几何模型如图1所示。由图1可知,松散润叶筒的筒体直径为1750 mm,长度为7000 mm,水平向下倾斜角为3°,筒体内设置短钉和抄板。烟叶通过输送带从左侧烟叶进料口进入润叶筒,依靠润叶筒倾角、旋转及自身重力的作用,向右侧X轴正方向运动,从出料罩底部输出[11]。

在生产现场的松散润叶筒中设置7个温度检测点(见图2),其中A、B、C、D、E截面处(距入口距离X分别为2 m、3 m、4 m、5 m和6 m)设置热电偶(热电偶型号HMR1010,杭州佐格通信设备有限公司,温度测量精度±0.1 K),检测该截面气相温度。F为循环气相出口处温度,G为烟叶出口处温度。

1.2 数值模拟

1.2.1 控制方程1)守恒方程[13-14]

质量守恒方程为

式中:ρ为流体密度/(kg·m-3);ui为i方向上的速度分量(i=1,2,3)/(m·s-1);t为时间/s;xi为坐标分量。

动量守恒方程为

式中:p为流体作用于微元体上的压力/Pa;uj为j方向上的速度分量(j=1,2,3)/(m·s-1);μ为流体黏性系数/(Pa·s-1);xi为坐标分量。

能量守恒方程为

式中:cp为比热容/(J·(kg·K)-1);λ为流体的传热系数/(W·(m·K)-1);T为温度/K。

2)Realizablek-ε湍流模型的湍动能和耗散率方程

由于Realizablek-ε湍流模型考虑了旋转和曲率[15],相比其他湍流模型更精确,故本文采用Realizablek-ε湍流模型,方程如下:

湍流动能方程(k方程)

Gk+Gb-ρε-YM+Sk

耗散方程(ε方程)

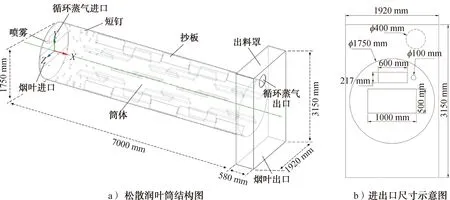
图1 松散润叶筒几何模型Fig.1 Model of moistening cylinder

1.2.2 网格划分网格划分对仿真的准确性至关重要。使用ICEM CFD软件对物理模型计算域进行松散润叶筒网格划分(如图3所示),采用四面体非结构化网格,抄板和短钉局部加密。为验证网格无关性,将网格数分为994 505、1 812 437和3 379 639,网格正交质量大于0.35。当工况一定时,对网格进行无关性验证,得到松散润叶筒轴线处气相的温度分布,结果如图4所示。由图4可知,当网格数为1 812 437和3 379 639时,沿轴线的气相温度分布基本相同,因此网格数选用1 812 437即可符合要求。

图2 检测点位置分布Fig.2 Location distribution of inspection points

图3 松散润叶筒网格划分Fig.3 Meshing of tobacco leaf moistening cylinder

1.2.3 边界条件和数值计算方法根据某厂松散润叶筒的实际工况运行参数,设定计算模型的边界条件及参数设置(见表1)。设置模拟烟叶密度为1100 kg/m3,烟叶比热容为1680 J/(kg·K),烟叶初始温度为298.2 K,烟叶初始含水率为12.00%[16]。喷雾采用压力旋流喷嘴雾化模型,喷雾喷射角为45°;松散润叶筒进行逆时针旋转,速度为10 r/min,筒体倾角为3°。

为简化计算量,对模型作如下假设:1)松散润叶筒内部各气体均为不可压缩的理想流体;2)松散润叶筒壁面均为绝热壁面,忽略其热损失;3)松散润叶筒内部温度不高,因此忽略辐射传热。

在ANSYS Fluent19.2中进行数值求解,计算采用稳态全隐式求解器,瞬态项格式为二阶精度迎风式,压力-速度耦合采用 SIMPLE 算法,收敛性和速度残差均为 10-3,能量残差为10-6,迭代步长为 0.01 s,每个时间步长迭代次数为20次[15]。

2 结果与讨论

2.1 稳态下的温度场特征

2.1.1 模拟结果验证由于计算出的温度云图剖面上有温度分布,本文直接选取垂直剖面中间9个点,取平均值求得该区域的气相(烟叶与液态水的混合物)温度;同时,在烟叶相中取6个点取平均数得烟叶温度。取样点位置如图5所示。

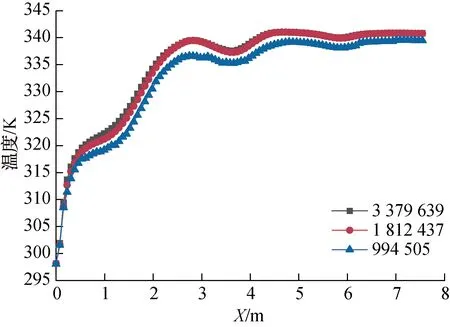
图4 网格无关性验证Fig.4 Grid independence verification

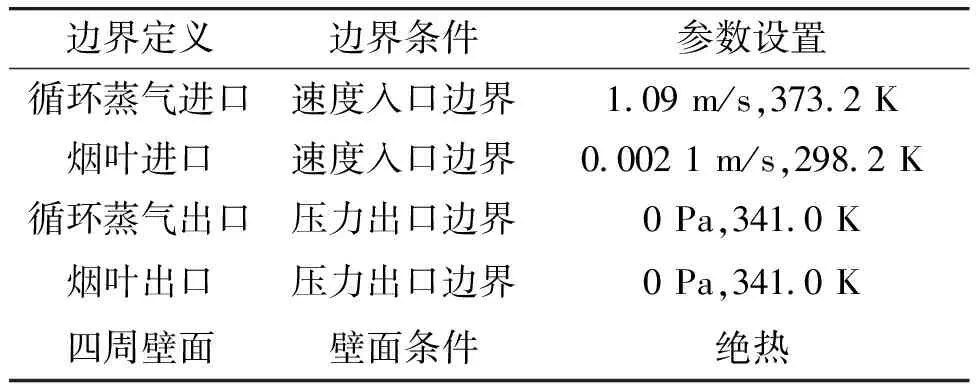
表1 边界条件及参数设置Table 1 Boundary conditions and parameter settings

根据模拟计算松散润叶筒温度分布,提取并计算各截面温度及两处出口处温度(出口F、G温度亦取管道平均值)。计算结果与实际生产过程中对应位置处热电偶所测得数值进行对比,以进行可靠性验证,结果如图6所示。由图6可知,总体上温度的绝对误差小于4.0 K,各检测点相对误差小于1%,平均绝对误差为2.0 K,平均相对误差为0.6%,模拟值与检测值吻合。因此,本文所建立的CFD模型可以用于松散润叶筒内部的温度场模拟。

2.1.2 松散润叶筒内部温度场特征温度分布云图如图7所示。由图7可知,进口处水蒸气和雾化水温度为373.2 K,进料口烟叶温度为298.2 K,在松散润叶筒进口处垂直方向上有较大的温差,上部温度高于下部。

图5 数值模拟中温度测量取样点Fig.5 Temperature measurement sampling points in numerical simulation

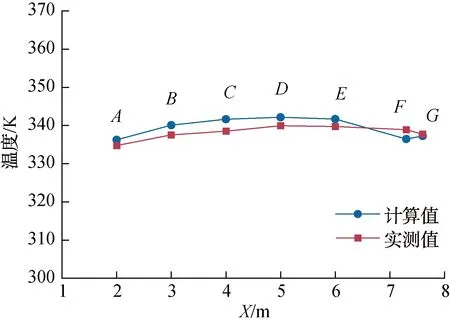
图6 可靠性验证Fig.6 Reliability verification

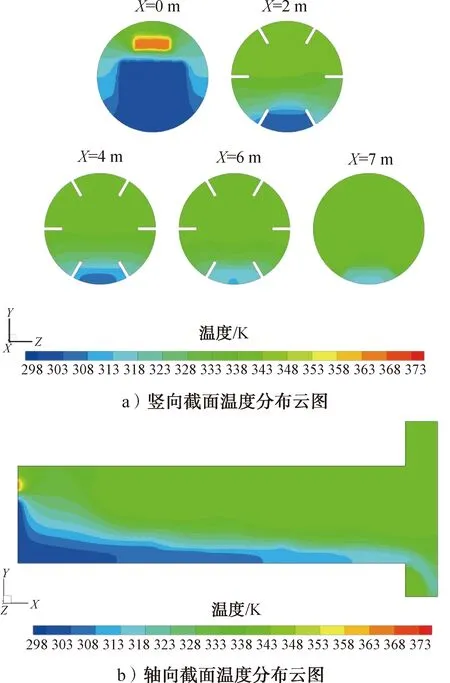
图7 温度分布云图Fig.7 Temperature distribution nephogram

在松散润叶筒内部,上部气相温度较高且分布均匀;在烟叶向出口方向运动的过程中,烟叶与气相发生对流传热,温度逐步升高,在松散润叶筒中后部烟叶温度趋近于气相温度,垂直方向上温度分布趋于均匀。烟叶相在计算中先简化成位于润叶筒底部。由于内部发生热传导的速率较慢,垂直方向上也存在一定的温度梯度。

气相和烟叶温度曲线如图8所示。由图8a)可知,气相温度随着轴向位置呈现分段变化,在X为0～4 m段气相温度迅速升高,且升高的速率越来越慢,最终温度达到341.0 K左右;在X为4～7 m段,气相温度基本保持不变,约为341.0 K。烟叶的初始温度为298.2 K,X轴方向上烟叶温度稳步上升,最终出料口烟叶温度达326.3 K,与实测值(333.2 K)相比,其相对误差在2.1%以内。

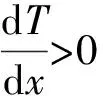
图8 气相和烟叶温度曲线图Fig.8 Gas phase and tobacco leaf temperature curve

因此,松散润叶筒不采用换热器的冷热流体逆流操作加大温差和传热速率,而用并流操作维持向烟叶相对稳定的传热、传质。

2.1.3 气相与烟叶相之间的对流传热气-固两相之间的热流密度计算公式如下:

q=h×(tf-tw)

式中,q为单位面积上两相之间在单位时间内交换的热量,称作热流密度/(W·m-2);h为表面对流传热系数(W·(m2·K)-1);tf、tw分别为流体和烟叶相表面的温度/K。

本文模拟得到气相与烟叶之间平均对流换热系数为29.25 W/(m2·K)[17],松散润叶筒轴向热流密度变化曲线如图9所示。由图9可知,热流密度随着轴向位置呈先升高后降低的阶段式变化,在x=2.5 m处,热流密度最高,达884.81 W/m2。由于松散润叶筒中部两相之间温差最大,可达30.3 K,因此,松散润叶筒中部位置在较大的传热推动力下热流密度最高,传热效果最好。

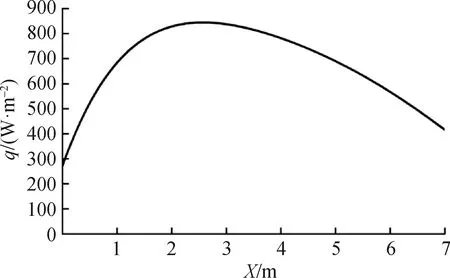
图9 松散润叶筒轴向热流密度变化曲线Fig.9 Variation curve of axial heat flow density of moistening cylinder

2.2 松散润叶筒内部烟叶分布云图分析

烟叶分布云图如图10所示。由图10可知,烟叶相进入筒体后主要集中在筒体下半部,在筒体倾角的作用下,向X轴正方向运动,最终从出料罩底部排出。

进料口烟叶的质量分数为0.88,烟叶含水率12.00%。随着烟叶相运动,水蒸气和雾化水持续向烟叶相传质,烟叶含水率逐渐升高。由于喷头指向右边,故右侧烟叶含水率较高,如X=4处截面。在烟叶相向X正方向运动过程中,混合物逐渐趋向均匀分布。

轴向烟叶含水率变化曲线如图11所示,松散润叶筒内部轴向烟叶含水率由图5中的6个点计算平均值得到。由图11可知,在进料口处,烟叶含水率为12.00%,轴向烟叶含水率呈递增趋势,最后出料口烟叶平均含水率达到17.21%,接近实际生产中用烘箱法测得的18.20%,相对误差小于5.8%。

2.3 筒体倾角对温度分布和烟叶含水率的影响

选定喷雾喷射角为45°,探究筒体倾角分别为3°、5°、8°的不同工况下,松散润叶筒内部两相温度和含水率的变化。

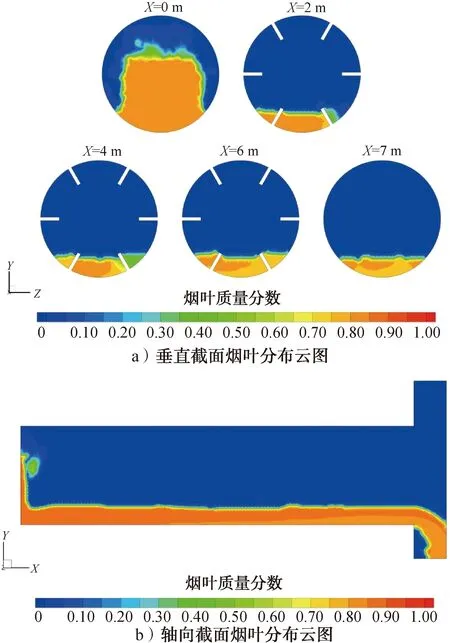
图10 烟叶分布云图Fig.10 Cloud chart of tobacco leaf concentration distribution

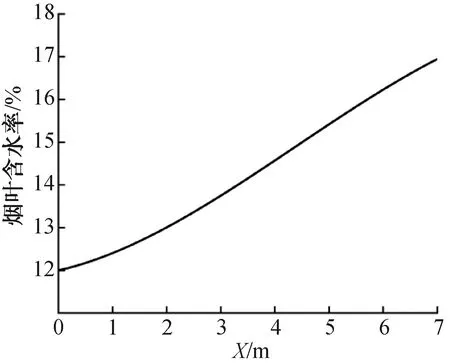
图11 轴向上烟叶含水率变化曲线Fig.11 Change curve of moisture content of tobacco leaves in axial direction

筒体倾角与温度、含水率关系如图12所示。由图12a)可知,不同筒体倾角工况下,筒内气相温度在同一位置的波动差异很小;随着倾角的减小,烟叶温度升高速率加快,当倾角为3°时,终端烟叶温度最高可达326.3 K。说明在倾角较小的情况下,物料停留时间相对较长,使烟叶与气相间的换热更为充分。由图12b)可知,烟叶含水率呈分段式变化, 在X为0～1 m段,不同倾角下烟叶含水率基本维持不变,说明在这一阶段加湿效果不明显;在X为1～7 m段,筒体倾角越小,烟叶含水率越大,说明倾角较小时,停留时间相对更长,烟叶能从气相中获得更多的水分。

烟叶进出口温差和含水率差如图13所示。由图13可知,倾角越小,其温差和含水率差越大。其原因是,随着筒体倾角变大,烟叶在滚筒内的滞留时间缩短,传热和传质不充分,使烟叶温度和含水量偏低。综合考虑,筒体倾角选为3°。

图12 筒体倾角与温度、含水率关系Fig.12 Relation between barrel inclination and temperature, water content

图13 烟叶进出口温差和含水率差Fig.13 Temperature and water content difference between tobacco leaf imports and exports

2.4 喷雾喷射角对温度分布和烟叶含水率的影响

选定筒体倾角为3°,探究喷雾喷射角(分别为15°、30°、45°、60°、75°时)对出料口烟叶含水率的影响。喷射角的定义如图14所示。烟叶进出口温差和含水率差如图15所示。由图15可知,喷雾喷射角对滚筒内部温度分布没有明显影响,进出口温差均约为28.0 K,变化在1.0 K左右,相对误差在5.3%以内。在不同喷雾喷射角的条件下,烟叶进出口含水率差均约为5%,出口含水率均为17%左右,变化幅度较小,相对误差在5.7%以内。由此可知,喷雾喷射角与烟叶温度和含水率变化之间没有明显相关性,综合考虑,喷淋装置喷射角选为45°。

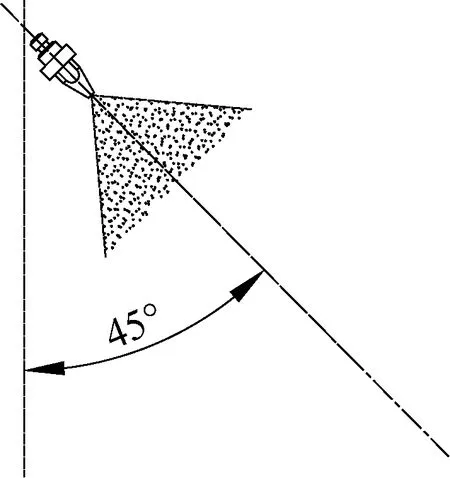
图14 喷射角定义示意图Fig.14 Schematic diagram of spray angle definition

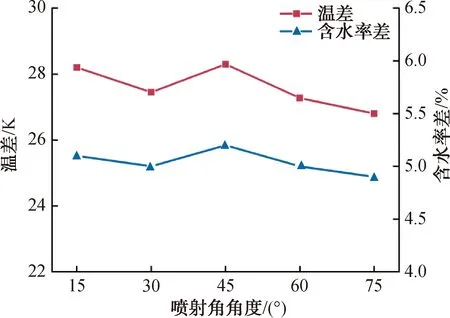
图15 烟叶进出口温差和含水率差Fig.15 Temperature and water content difference between tobacco leaf imports and exports

3 结论

以实际松散润叶筒为原型,采用 Fluent 仿真软件对烟叶加湿过程进行模拟,对温度分布、烟叶含水率分布等进行系统性分析,得到以下结论:

1)松散润叶筒内气相温度数值模拟结果与实验数据较为吻合,各检测点温度相对误差小于1%,平均绝对误差为2.0 K,平均相对误差为0.6%,所建立的模型真实有效。

2)通过计算得到松散润叶筒内的温度场分布,轴向气相温度在X=0～4 m段迅速升高,后半段稳定在341.0 K左右,平均相对误差小于0.6%;烟叶温度稳步上升,最终出料口烟叶温度达到326.3 K,相对误差在2.1%以内;气相和烟叶间的热流密度沿轴向先升高后降低,在X=2.5 m处,热流密度最高,达884.81 W/m2。

3)松散润叶筒内初始烟叶含水率为12.00%,随着烟叶向出口移动,雾化水和气相中水蒸气向烟叶传质,含水率逐步升高,最终出料口烟叶含水率达17.21%,相对误差在5.8%以内。

4)依据有效的模型选取松散润叶筒最优操作工况,当筒体倾角为3°、喷雾喷射角为45°时,烟叶加湿加热效果最佳,出口烟叶含水率达17.21%,温度达到326.3 K。

本文对松散润叶筒内部温度场和烟叶含水率分布进行了模拟和分析,为使松散润叶筒内烟叶升温加湿效果更好,除了优化调整筒体倾角和喷雾喷射角之外,未来可改变抄板安装角度、转筒转速等方法来改善烟叶运动轨迹,也可以通过对烟叶运动轨迹的可视化计算,利用ANSYS软件包中的ROCKY软件对滚筒内部烟叶颗粒的运动规律和特点进行深入研究。