高速铁路埋入式桩板结构分界路基填高研究

徐玉龙 孙红林 曾长贤

中铁第四勘察设计院集团有限公司， 武汉 430063

桩板结构因其优越的刚性特征在高速铁路路基软土、岩溶、交叉工程、过渡段中［1-3］广泛应用，近年来逐渐被公路领域借鉴采用［4-5］。非埋式桩板结构是将轨道结构直接置于承载板上，其计算理论与连续钢构桥相同，比较成熟。而埋入式桩板结构的承载板与轨道结构之间存在柔性路基填料，构成了柔性路基-刚性桩板结构的刚柔互耦复杂结构体系，导致整个结构体系的荷载传递、结构计算都趋于复杂，计算理论未得到详细研究，结构计算与设计存在不安全因素。

埋入式桩板结构分为浅埋式和深埋式桩板结构，两者结构形式和结构设计荷载有所不同。结构形式主要表现为承载板上路基填高不同（图1），TB 10106—2010《铁路工程地基处理技术规程》定义浅埋式桩板结构中承载板通过基床表层与轨道结构连接，即浅埋式桩板结构与轨道结构之间仅有基床表层。高速铁路路基的基床表层多为0.4 m 厚级配碎石，即路基填高0.4 m 为浅埋式桩板结构与深埋式桩板结构的分界填高。结构计算上，浅埋式和深埋式桩板结构的区别在于设计荷载的不同（表1），TB 10106—2010 规定深埋式桩板结构计算仅考虑列车、轨道及路基填料构成的恒载，浅埋式桩板结构除考虑恒载外，还需要考虑列车竖向动力作用、列车水平力及温度变化作用。

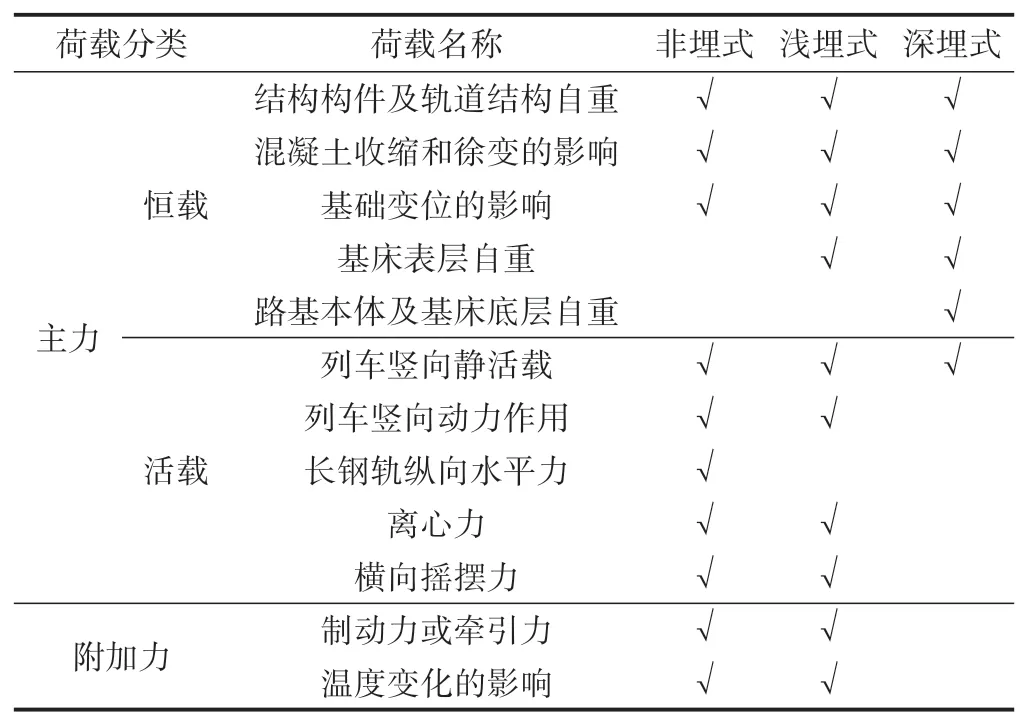
表1 桩板结构设计荷载

在目前设计荷载框架下，埋入式桩板结构的分界路基填高设置为厚度仅0.4 m 基床表层的合理性未见文献详细论证，结构计算可靠性存疑。实际工程设计中普遍认为基床表层厚度作为浅埋式与深埋式桩板结构的分界高度不可靠，因而人为放大分界路基填高，埋入式桩板结构计算较为混乱，结构设计存在不安全或过于保守的问题。故有必要对列车动力作用、列车水平力、温度变化作用在柔性路基结构中的传递作用进行论证，确定与设计荷载相匹配的埋入式桩板结构分界路基填高，提高桩板结构设计合理性与安全性。本文主要借助既有监测数据，采取理论分析的方法，对列车动力作用、列车水平力、日照温差作用在路基中的影响深度进行研究，确定合理的埋入式桩板结构分界路基填高，为桩板结构的准确计算提供依据。

1 列车竖向动力作用影响深度

1.1 基于有砟轨道监测数据的动应力影响深度

在国内高速铁路修建之初，多家研究机构对国内外铁路动荷载在路基基床结构的衰减情况进行了总结，动荷载在路基结构内竖向动应力衰减情况见图2。监测数据主要针对有砟轨道铁路，包括国内木枕、混凝土枕路基及德国、波兰的既有线实测数据［6-8］。

由图2 可知：列车动应力主要集中在1 m 范围内，埋深1 m 左右的动应力基本衰减为初始值的30%左右。3 m 深度动应力衰减系数基本小于0.2［6］。铁路设计中，一般列车荷载产生的动应力与路基自重应力之比小于0.2时，就不再考虑动应力影响。按此标准，可认为有砟轨道动应力影响深度控制在3 m以内。

1.2 基于无砟轨道实测的动应力影响深度

近年来，随着高速铁路的大量建设，越来越多的高速铁路动应力实测数据不断出现，中国铁道科学研究院集团有限公司对武广、郑万、京沈等高速铁路的实测研究显示，路基面动应力幅值普遍位于9.6 ～18.77 kPa，沿线路纵向分布距离8.0 ～ 10.1 m［8］。根据路基表面的动应力实测数据，再结合Boussinesq 理论，可计算动应力在路基结构内的衰减情况，即

式中：σz为竖向动力；P0为荷载强度；m为a0与b0的比值，n为z与b的比值，a0，b0为长方形荷载边长的一半，z为深度。

荷载宽度a0缺少实测数据支撑，按保守考虑，取支承层宽度3 m；荷载长度b0按最大10.1 m 计算；路基面动荷载P0取最大幅值18.77 kPa。

Boussinesq 理论是基于半无限空间均匀弹性体假设的，而路基为填土层弹性模量不同层状结构体，需采用基于Odemark 模量与厚度当量假定的等效厚度法，将不同弹性模量的路基土层折算成与标准层同模量的等效层厚。等效厚度，其中E为需折算结构层的弹性模量，E0为标准层弹性模量，这里取研究范围内实际厚度最大的基床底层，h为需折算结构厚度。各层等效厚度见表2。可知，路基面以下实际厚度3 m的等效厚度为3.01 m，两者接近。

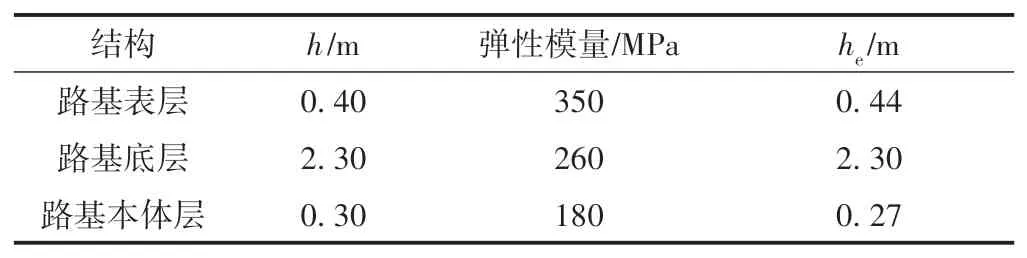
表2 路基结构等效厚度

根据Boussinesq 理论计算得到的路基表面下3 m的动应力随深度变化情况见图3。可知：路基面以下深度3 m 的动应力衰减为9.9 kPa。该计算按照保守考虑，将路基面动载视为均布荷载、路基面动荷载和加载长度均取最大值时，结果也相应偏大。

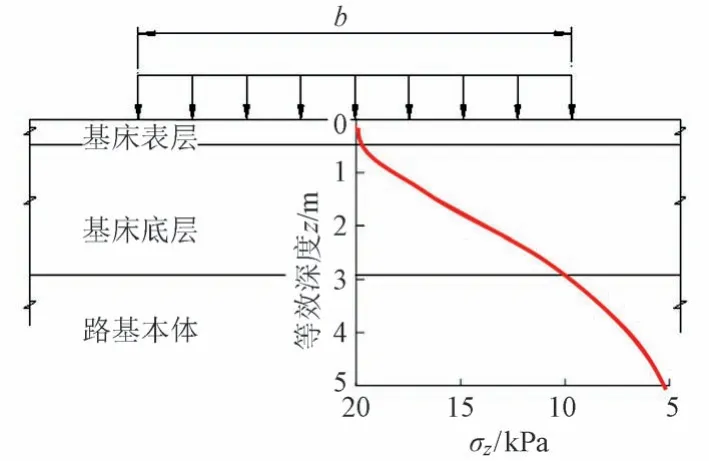
图3 路基结构内动应力衰减

1.3 基于无砟轨道路基动荷载分配简化模型的动应力影响深度

高速列车通过路基结构时，路基、轨道、车辆间形成复杂的振动系统，车轮对轨道的冲击，加之轨道的不平顺性会产生周期性激振荷载。中国铁道科学研究院集团有限公司根据大量实测数据和数值计算，提出无砟轨道路基动荷载分配简化模型［8］，明确轨道结构的支承层上动荷载形式与大小，继而采用Boussinesq 理论计算动应力在支承层与路基结构的衰减情况。该模型假设单个轴载在支承层或底座板顶面形成的动荷载沿纵向呈三角形分布，最大值为σdmax，计算式为

式中：Pd为动轴重；2e'为单轴荷载作用下支承层或底座板顶面动荷载横向分布宽度，e'=（bg-d）/2，bg为沿横向分布长度，为轨道板宽度，两边平均分布，中间不受力，d为支承层或底座板中部动荷载为0 的区域宽度；l为单轴荷载作用下支承层或底座板顶面动应力纵向分布长度，实测3.5 m；Ps为静轴重，高速铁路取值为200 kN；α为动力系数，实测值1.20～1.35，取1.35。

以CRTSⅢ型板为例，轨道板bg= 2.5 m，d= 0.85 m，获得横向分布宽度e'= 0.825 m，单个轴载动荷载在支承层动荷载最大值（σdmax）为93.5 kPa，与TB 10621—2014《高速铁路设计规范》推荐100 kPa 基本接近。支承层、基床表层等均采用Odemark 的模量与厚度当量假定确定，各层等效厚度见表3。

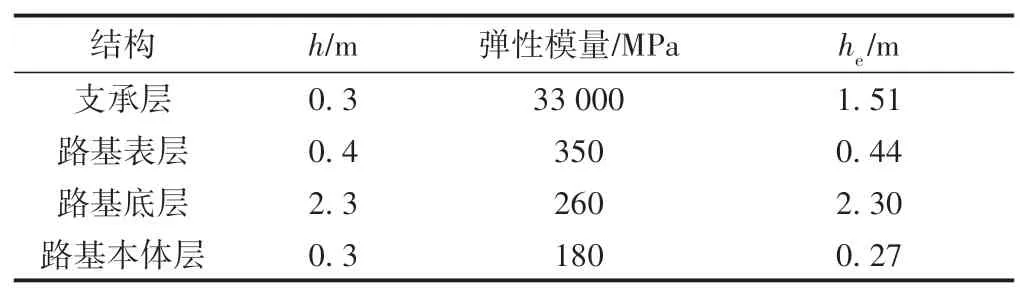
表3 轨道与路基结构等效厚度

考虑1 个转向架的2 个轴载叠加效应，荷载分布如图4所示，图中l0为轴距。以CRH380型动车组为例，其l0为2.5 m。由于轴载形成的荷载分布较为复杂，在采用Boussinesq 理论计算时，可采用多个矩形与三角形角点附加应力计算方法获得，但由于分布形式过于复杂，计算不便。因此，计算某点动应力形式时，在该点表面处建立笛卡尔坐标系，根据布氏理论任一点（x，y）在坐标原点O的竖向应力（dσz）随深度（z）的变化为

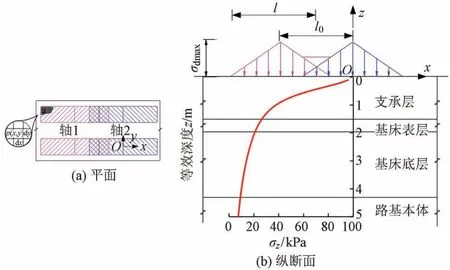
图4 半幅轴载荷载中心的垂直应力随等效深度的变化

式中：σz为坐标原点处随深度变化的动应力；x、y、z为坐标轴向；p（x，y）为坐标（x，y）处的分布力；r=为整个荷载作用域。

计算得到三角形荷载最大值处的动应力沿着支承层、路基基床结构及本体的扩散见图4（b）。可知，采用该模型在路基表面处动荷载接近26.5 kPa（等效深度1.51 m 处），与实测数据基本相符；在路基面以下实际深度3 m（对应图中等效深度约4.6 m 处）动应力最大值为8.4 kPa，与矩形荷载下路基面以下深度3 m的动应力衰减计算值9.9 kPa 较为接近。3 m 处动应力小于路基自重应力20%，说明无砟轨道铁路动应力影响深度基本在3 m范围。

从早期有砟轨道实测数据、近年来的高速铁路无砟轨道实测数据、高速铁路动应力修正理论等方面计算论证显示，列车动应力在深度3 m 左右基本衰减到10 kPa以内，此时动应力小于路基自重应力的20%，工程上可不再考虑动应力影响。此外，涵洞结构与路基结构、轨道结构构成刚柔互耦体，结构形式接近于桩板结构与路基、轨道结构。TB 10621—2014 明确规定，涵洞结构的填土厚度大于3 m时，可不计列车动力作用。针对日本无砟轨道的众多实测案例中也多显示动应力影响深度约3 m［9-10］，经类比可认为，高速铁路列车动应力影响深度在3 m以内。

2 水平力影响深度

桩板结构设计荷载中的水平力主要有列车横向的离心力、摇摆力及纵向的制动力与牵引力。埋入式桩板结构中，水平力需要经由柔性基床结构传递到承载板上。基床结构中的基床表层一般为级配碎石，基床底层砾石土、砂类土的A、B 组填料。这些材料本质为散体材料。对于竖向荷载在散体材料的传递问题，目前有地基加固的换填垫层实测数据支撑及成熟的荷载扩散模型，而散体材料能否传递水平力，缺少完备的理论和试验支撑。

关于无砟轨道下框架涵洞的一般经验是，覆盖层厚度大于1 m 时，交通荷载的水平荷载可忽略不计［8］，但未见详细的论证。基床结构作为散体材料，水平力传递时通过颗粒间的弹性流动、颗粒的变形产生能量耗散，而这种弹性流动又与连续介质的应变类似，即力在散体介质中的耗散，类似于连续介质中产生的应变能耗散。据此，考虑进一步采用连续介质力学来分析水平力的传递。

文献［11］指出Holl 曾获得半无限空间弹性体矩形水平均布荷载作用到矩形上的应力解析解（图5）。列车水平力通过轨道结构传递到路基面宽度（b）为支承层宽度3 m，加载长度（L）为单块轨道板长度5 m，在路基表面形成均布水平荷载。按照Holl 解析解，在荷载边界中点B处竖向应力和水平应力达到最大，得到B点不同深度的水平荷载衰减系数，见图6。由于Holl水平矩形荷载应力解析解与Boussinesq 理论都基于半无限空间弹性体假设，所以Odemark 模量等效厚度在此仍成立，各层等效厚度参见表2。

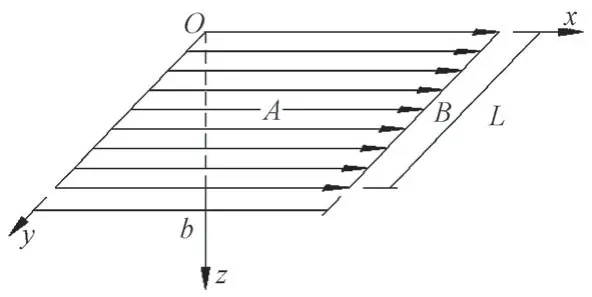
图5 水平荷载作用

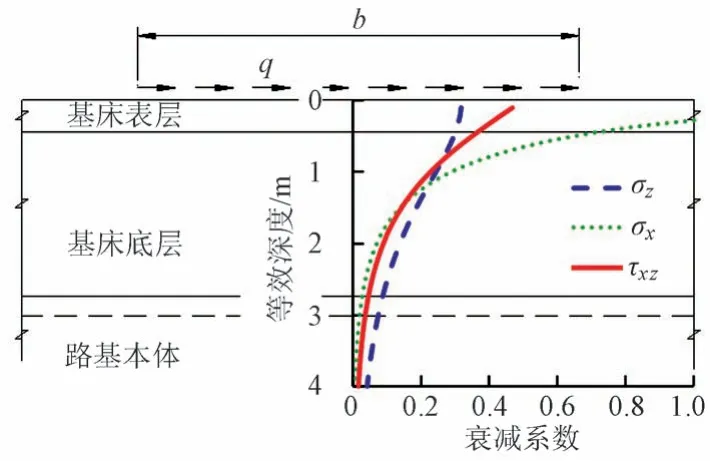
图6 水平荷载产生的应力随深度衰减情况

σz、σx、τxz分别为z方向竖向正应力、x方向水平正应力和剪应力，计算式为

其中

式中：q为水平荷载。

由图5、图6可知：水平荷载在半无限弹性体内，在深度1.0 m 范围内衰减最快；当深度达到1.5 m 时，水平荷载产生的应力基本衰减到作用在路基面水平荷载的20%。而深度达到3.0 m 时，σz、σx及τxz衰减系数分别为0.075、0.021、0.036。

以CRTSⅢ型板为例，列车横向的离心力（曲线半径6 000 m，设计时速350 km）、摇摆力及纵向的制动力与牵引力作用到单块轨道板上形成的矩形水平荷载强度分别为3.64、6.00、2.80 kPa，在3.0 m 深度竖向正应力σz分别衰减为0.27、0.45、0.21 kPa，水平正应力σx分别衰减为0.08、0.13、0.06 kPa，剪应力τxz分别衰减为0.13、0.22、0.10 kPa。需要关注的是竖向正应力和剪应力，当桩板结构置于3.0 m 处，竖向正应力σz会形成竖向荷载，剪应力τxz则会形成水平方向摩擦力，但两者在3.0 m 处衰减值非常小，对结构影响微弱。

3 温度影响深度

TB 10106—2023《铁路工程地基处理技术规程》中深埋式桩板结构设计荷载不含温度变化影响，即认为深埋式桩板结构上覆路基填料足够厚，会阻隔温度传递，无须考虑温度变化影响。温度变化主要为日照温差对结构的影响，日照温差对路基结构温度影响深度研究甚少。在针对京张铁路沥青混凝土的保温效果监测研究中，认为温度在路堤结构影响深度约0.3 m［12］；在针对季节性冻土区环境温度变化对加筋土挡墙内部温度场的影响研究中，发现挡墙内温度变化区域主要位于距面板和路面结构层底部3 m 内，距面板背部和路面层0 ～ 1 m 和1 ～ 3 m 可进一步细化为温度变化敏感区和缓和区［13］。

鉴于相关实测研究较少，采用理论计算的方法研究温度变化的影响深度。建立半无限大空间的非稳态一维热传导偏微分方程，对温度传递规律进行研究。热传导偏微分方程为

式中：T为温度，是时间t与距离x的函数；a为热扩散率。

假定整个半无限体的初始温度为0，初始条件为

路基结构接受的日照温差存在周期性变化，使x= 0 边界形成周期变化的温度，采用周期为2π/ω的弦函数来描述这种周期性温度变化；当距离无穷大时，温度趋近于0，偏微分方程的边界条件为

不同土岩体的热扩散率见表4［14-15］。路基基床及路基本体一般为A、B 组填料，采用土壤的热扩散率进行计算，即a取25.2 × 10-4m2/h。对于温度边界条件T=Asin（ωt），温度振幅（A）取15 ℃，相当于昼夜温差30 ℃；温度变化周期取24 h，即ω= 2π/24。

表4 不同物质的热扩散率

当边界条件x= 0，T为常数时，非稳定态热传导偏微分方程可采用分离变量法求解。但由于日照温差呈现周期性变化特征，x= 0 处T表现为随时间变化的函数，导致偏微分方程难以采用分离变量法求解，采用拉普拉斯变换求解该方程时，会出现不存在拉普拉斯逆变换的情况。而考虑到边界条件为周期型函数，且作用范围在正半无限空间，采用傅里叶正弦变换求解该微分方程，将T（x，t）进行正弦变换后得到

代入式（8）得到

式（13）为t的非齐次一阶线性微分方程，采用常数变易法进行求解，获得非齐次方程的通解为

式中：C为常量。

将初始条件代入式（14），可以获得C的表达式，即

由此得到正弦空间的解为

需要将该函数进行正弦逆变换才能得到T（x，t），正弦逆变换的形式为

式（16）在进行正弦逆变换时，kωe-ak2t/（a2k4+ω4）项只能获得积分形式的解。

因此整个通解为

其中

将A、a、ω等参数代入式（18），可获取T随时间和距离的变化图，积分部分可采用区间分割的数值积分算法获得。计算结果见图7。

由图7可知，温度变化影响深度较为有限，温度变化几乎波及不到深度1 m 处。由图7（c）可知，温度变化影响主要集中在0.5 m深度内。

不同地表深度时温度随时间变化曲线见图8。可知：不仅弦函数的振幅随着深度的增加急剧下降，相位也随着深度发生变化，表明温度传递具有滞后效应。

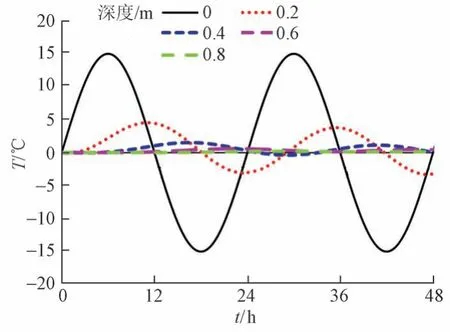
图8 不同地表深度下温度（T）随时间（t）的变化曲线

此外，从季节性冻土角度考虑温度影响，国内以及国外的季节性冻土冻结深度普遍不超过3.0 m，如中国东北地区和俄罗斯乌苏里江以东地区冻结深度1.5 ～ 2.4 m［16］，青藏高原邦达草原冻结深度2.2 m，毛垭坝草原冻结深度1.0 m，哈大铁路沿线最大冻结深度2.05 m［17］，甚至俄罗斯乌苏里江铁路高纬度冻结深度也不到3.00 m，为2.75 m。即使是环境温差较大的区域，冻结深度也一般局限在3.0 m 范围内。这从侧面反映出，环境温度变化在地下的影响深度有限，且集中在3.0 m深度以内。

综上，温度变化影响深度有限，一般不出超出3.0 m 范围。当承载板上柔性路基填料厚度不小于3.0 m时，可不考虑温度变化作用。

4 桩板结构分界路基填高

埋入式桩板结构中的浅埋式桩板结构设计荷载包括列车、轨道及路基填料构成的恒载以及列车竖向动力作用、列车水平力、温度变化作用等活载或附加力，而深埋式桩板结构设计荷载仅包括恒载。在保持当前设计荷载不变情况下，可根据列车竖向动力作用、列车水平力及温度变化作用三类荷载的影响深度最大值，确定埋入式桩板结构分界厚度。

控制埋入式桩板结构分界厚度的因素有：列车竖向动力作用、列车水平力、日照温差影响深度。列车竖向动力作用在3.0 m左右衰减系数约0.2，此时应力幅值衰减到10 kPa 以内，为路基自重应力的20%以下，工程上可不计其影响；而列车水平力在1.5 m 衰减系数就会达到0.2，且由于水平荷载较小，对桩板结构影响微小；日照温差影响深度更浅，主要集中在路基面以下0.5 m 范围内。综上所述，列车竖向动力作用影响深度最大，控制埋入式桩板结构分界厚度的关键因素为列车竖向动力作用。因此，以3.0 m 路基填高为界限，作为浅埋式桩板结构和深埋式桩板结构分界路基填高，可与当前的设计荷载匹配。

5 结论

1）路基结构内动应力在3.0 m 深度左右基本衰减为路基自重的20%以下，应力幅值衰减到10 kPa以内。

2）采用弹性理论分析列车水平荷载作用的影响深度，列车水平力在路基结构内1.5 m 深度范围内衰减最快，深度达到3.0 m 时，竖向正应力、水平正应力及剪应力衰减系数分别为0.075、0.021、0.036，对桩板结构影响微弱。

3）建立日照温差在路基结构传导的非稳定态热传导偏微分方程，并采用傅里叶正弦变换进行求解，获得日照温差影响主要集中在路基面以下0.5 m 范围内。

4）浅埋式桩板结构与深埋式桩板结构的分界路基填高主要受列车竖向动力作用控制，建议分界路基填高按3.0 m控制。