弹条折痕对DI弹条大圆弧断裂的影响

王敏 段玉振 陈应东 张宏亮

1.北京铁科首钢轨道技术股份有限公司， 北京 102206； 2.北京城建设计发展集团股份有限公司， 北京 100037；3.中铁城市发展投资集团有限公司， 成都 610213

DTⅥ2型扣件是针对于城市轨道交通地下线工程特点而研发的扣件，具有零部件少、施工便捷等特点。该扣件静刚度为（30 ± 5） kN/mm，单根弹条扣压力为8.25 kN，单根弹条弹程（中间弹条）为10.5 mm。

城市轨道交通扣件采用的e型弹条主要包含国铁Ⅲ型弹条和DI弹条。e型弹条应力最大位置为小圆弧内侧及跟端下侧［1-2］，如图1 所示。正常设计情况下，最大应力小于屈服强度。使用过程中两种弹条均有断裂情况发生。陈宪麦等［1］通过有限元计算研究表明，弹条弹程较大时弹条应力超过弹条材料屈服极限会引发弹条塑性变形，在列车荷载作用下导致弹条断裂，并且在现场波磨引起的钢轨振动引发弹条共振，也会促使弹条发生断裂。余鸿［3］研究发现弹条安装不规范会增加弹条内部应力，导致弹条受力不均，从而引起断裂。赵阳磊等［4］从材料金相组织角度研究认为弹条热处理工艺不佳时，在列车荷载作用下，弹条高应力位置表层材料会发生疲劳损伤，引发断裂。张松琦等［5］对非正常断裂弹条研究并提出DI 弹条生产模具和安装工艺的优化建议，指导e型弹条设计、安装及后期维护。

图1 正常状态下e型弹条应力分布（单位：MPa）

目前对于e型弹条断裂的原因分析及改进建议主要集中在常规小圆弧位置发生断裂现象的情况，但个别城市地铁中发生e 型弹条大圆弧位置发生断裂现象。吴浩等［6］针对于这一现象采用非线性有限元和模态分析方法研究，得出在e 型弹条2 阶固有频率共振时弹条最大应力出现在大圆弧位置，且轨距挡块与弹条之间的相对微动、摩擦将导致弹条2 阶固有频率减低，引起弹条在大圆弧位置发生振动断裂。该项研究对于e型弹条发生大圆弧断裂的原因探究具有一定的指导意义。

在某地铁线路中发生DI弹条大圆弧断裂地段，现场查看发现钢轨并无波磨，因此该断裂非共振引发。经踏勘发现，现场安装同批次DI弹条在大圆弧位置存在明显折痕迹，属弹条生产加工产生的初始缺陷，如图2 所示。本文通过非线性接触有限元法对DI 弹条的上述异常情况进行分析，以期解释在无波磨共振影响地段DI弹条大圆弧断裂原因。

1 有限元模型

在有限元分析软件中进行扣件精细化建模，采用实体单元对DTⅥ2 型扣件各部件按照实际尺寸建模。部件包括锚固螺栓、钢轨、弹条、铁垫板、轨距挡板、平垫圈以及轨枕。建立车辆-轨道多体动力学模型，通过模拟真实地铁车辆和线路，提取列车行驶过程中的轮轨垂向、横向力，作为有限元分析软件中扣件精细化模型的荷载输入。在钢轨对应位置施加荷载，并设置幅值使荷载随时间变化，模拟列车通过。

1.1 弹条材料参数

弹条采用60Si2Mn 弹簧钢，弹条材料本构关系采用理想线性强化弹塑性模型。根据GB/ T 1222—2016《弹簧钢》，弹条材料抗拉强度不小于1 570 MPa，屈服强度不小于1 375 MPa，伸长率不小于5%，断面收缩率不小于20%。模型中弹条材料屈服强度取1 375 MPa，抗拉强度取1 570 MPa，强化模量E1= 0.1E，其中E为弹性模量。扣件各零部件材料特性见表1。

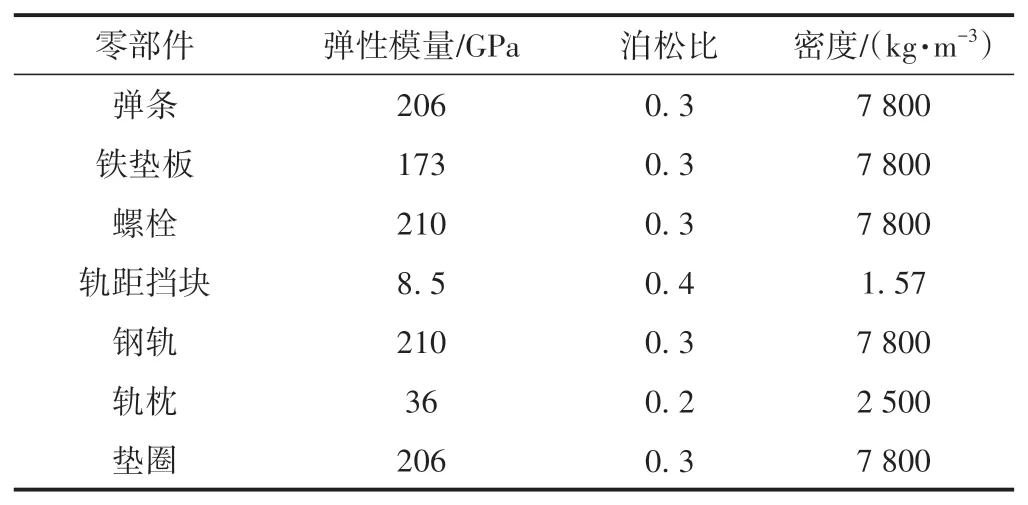
表1 扣件各零部件材料特性

1.2 有限元模型

用Soild实体单元进行离散处理，建立扣件各部分有限元模型并进行装配，见图3。

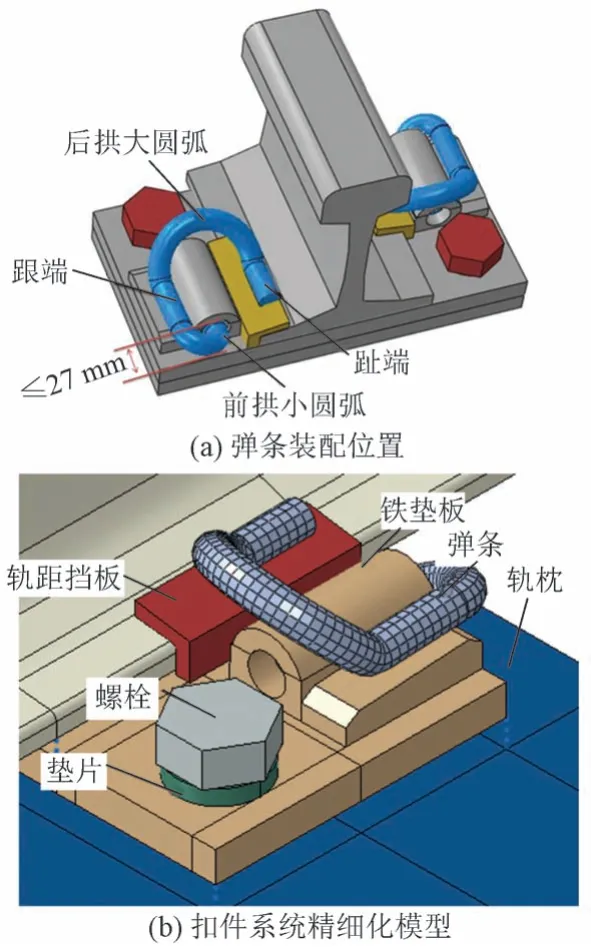
图3 有限元模型

为研究大圆弧存在折痕对弹条受力的影响，分别建立无折痕、有折痕的弹条模型进行有限元分析。有折痕的模型中，折痕采用生死单元法模拟，通过在扣件的对应位置删除部分单元来模拟弹条折痕造成的损伤，折痕深度按照1 mm 考虑。为了精确表示折痕，对弹条的网格进行细化，并将弹条大圆弧处网格单元类型由六面体单元更换为四面体单元，见图4。

图4 有折痕的弹条模型

1.3 接触关系设置

为研究弹条的断裂机理，清晰反映弹条的受力特征，同时为了保证计算精确度，真实模拟弹条的受力状态，采用非线性接触理论处理弹条与铁垫板之间的面-面接触关系，见图5。设置边界条件时，钢轨两端采用对称约束模拟钢轨在纵向无限长，螺栓螺纹处、轨枕底面采用绑定约束。

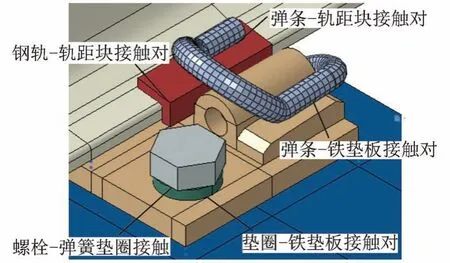
图5 各部件接触关系

1.4 弹条模型验证

为分析弹条在规范安装工况下的静力性能并验证模型的正确性，模型中将弹条后拱小圆弧内侧与铁垫板支座之间距离设置为6 mm，加载弹程设置为10.5 mm，得到弹条变形云图，见图6。可知，弹条趾端变形最大，中肢部位变形最小，弹条前拱大圆弧中点垂向变形为7 mm。根据计算结果，此时弹条扣压力为8.46 kN，与弹条设计值相差2.5%，此模型可以用来进行静力分析。

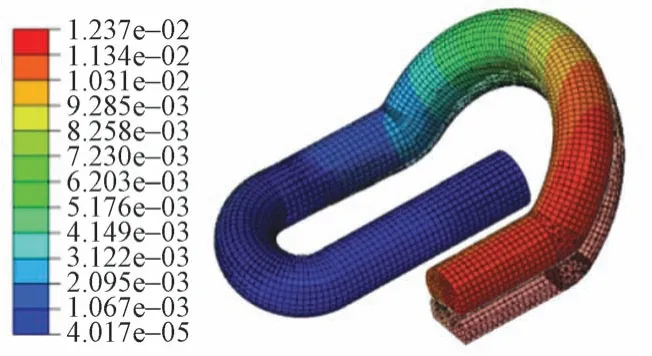
图6 弹条变形云图（单位：m）

2 轮轨力仿真计算

2.1 车辆及线路参数

根据GB 50157—2013《地铁设计规范》表4.1.5，地铁车辆取A 型车，车辆轴重取极端值，即最大轴重17 t，最小轴重14 t；车辆定距为15.7 m，固定轴距为2.5 m。

根据真实线路情况，模型中线路设定为100 m 直线 + 100 m 缓和曲线 + 100 m 曲线 + 100 m 缓和曲线 +100 m 直线，共500 m。轨道不平顺采用美国五级谱。根据文献［7］确定相关参数，并导入分析软件，不平顺激励的长度为0 ～ 500 m，即全线存在不平顺激励。

2.2 工况设置

为对比各参数对扣件弹条受力状态的影响，设置12种计算工况，见表2。

2.3 仿真计算

对地铁车辆在施加不平顺激励的线路行驶时的轮轨垂向、横向力展开仿真计算。以工况1为例，列车行驶时的轮轨力时程曲线见图7。可知，由于施加了不平顺激励，在初始运行阶段车身出现抖动，使得轮轨垂向力和横向力有异常峰值，导致计算结果失真。因此，后期处理中将异常峰值剔除后，作为荷载输入，代入扣件有限元模型进行计算。

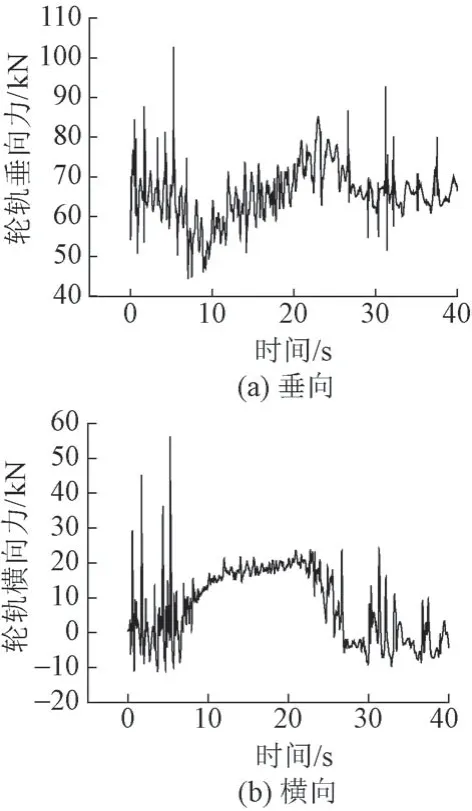
图7 轮轨力时程曲线

3 弹条动力学计算

3.1 评价指标

弹条为金属塑性材料，在安装过程和列车振动荷载作用下承受应力，产生变形。过大的变形使弹条达到屈服极限，是造成其伤损劣化的重要原因。因此，分析弹条受力时应选取合理的评价指标，即材料的强度准则。DI 弹条60Si2Mn 材料定义为塑性材料，弹条在列车荷载作用下发生振动，承受拉压、扭转、剪切力等。第四强度理论考虑了三个主应力的共同作用，能更好地描述实际受力状态。因此，采用第四强度理论（Mises准则）作为控制评价指标。

3.2 无折痕DI弹条动力学计算结果及分析

对12 种工况下无折痕状态的DTⅥ2 型扣件DI 弹条进行动力学计算。工况1—工况12下计算得到的最大Mises 应力依次为1 131、1 172、1 150、1 161、1 183、1 198、1 169、1 202、1 177、1 187、1 199、1 207 MPa，最大应力均发生在前拱小圆弧处。

以工况1 为例，提取无折痕的DI 弹条Mises 应力分布，见图8。可知，弹条前拱和跟端应力较大，Mises应力最大值出现在前拱小圆弧内侧，达到了1 131 MPa，尚未达到弹条材料的屈服强度，弹条整体为安全状态，没有发生断裂的风险。12种工况下无折痕DI弹条最大Mises应力均符合这一特征。

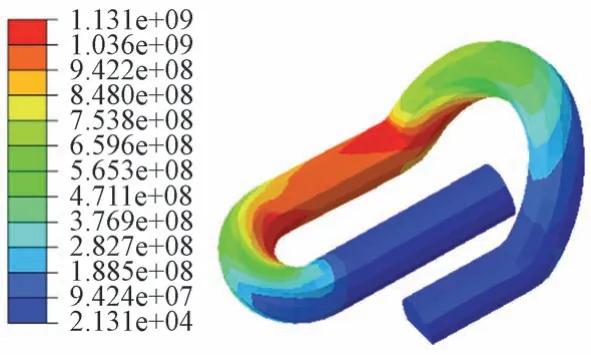
图8 工况1下弹条Mises应力分布（单位：Pa）

3.3 有折痕DI弹条动力学计算结果及分析

对12 种工况下有折痕状态的DTⅥ2 型扣件DI 弹条进行动力学计算，计算结果见表3。可知：最大应力均发生在折痕处。

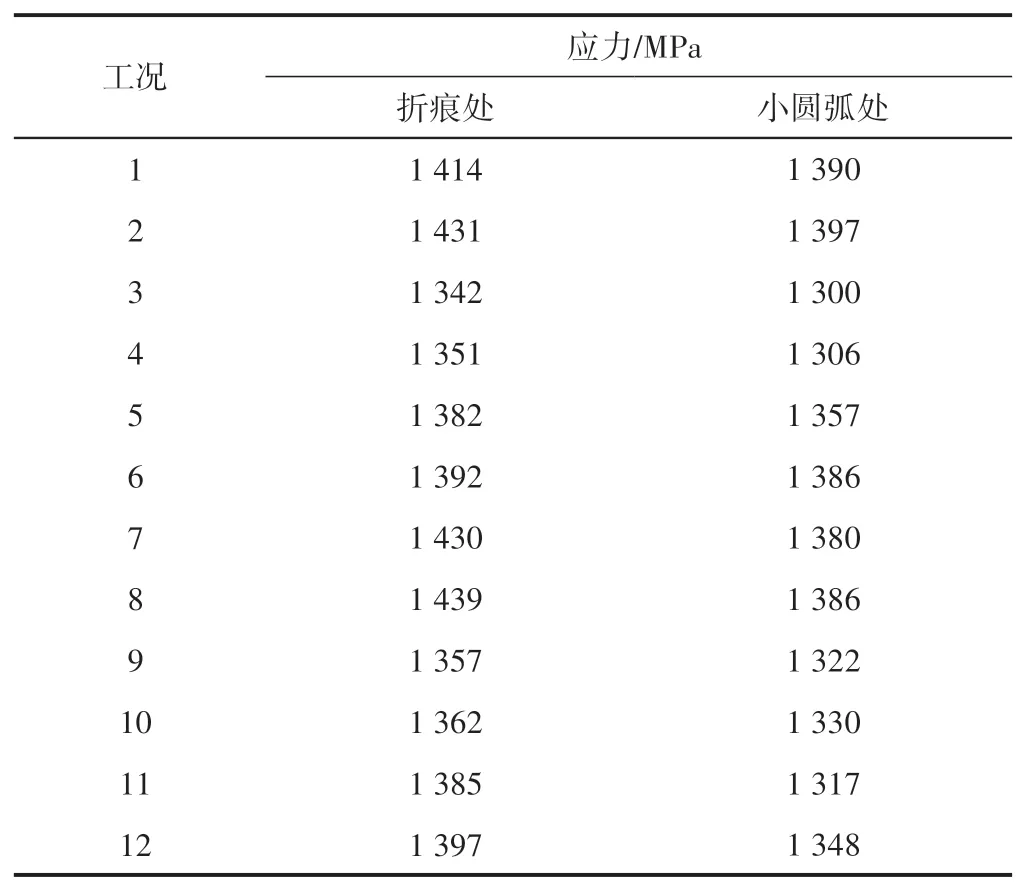
表3 有折痕的DI弹条Mises应力

以工况1 为例，提取有折痕的DI 弹条Mises 应力分布及折痕处的Mises应力，见图9、图10。可知，添加折痕以后，在相同的工况下，弹条后拱小圆弧和折痕处的应力较大；弹条最大应力出现在折痕处，最大值为1 414 MPa，已经超过了屈服强度。说明在有折痕的情况下，弹条在折痕处出现应力集中，折痕处最大应力已超过小圆弧位置并发生了塑性变形。虽然材料有屈服强化的特性，折痕所在截面强度弱于其他截面，成为弹条受力的薄弱点。在列车长期往复荷载的作用下，折痕位置存在发生疲劳破坏断裂的风险。

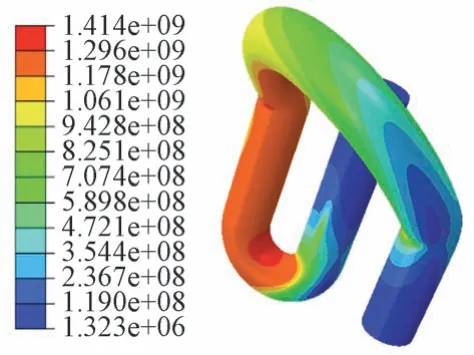
图9 弹条Mises应力分布（单位：Pa）

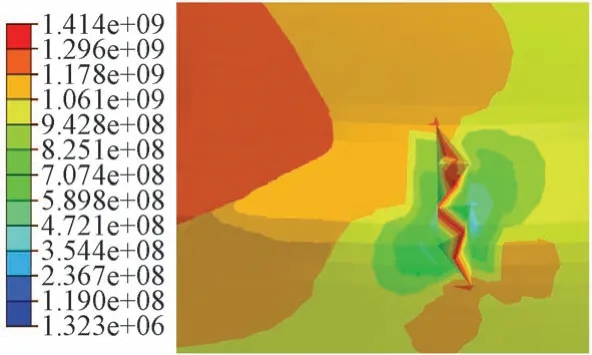
图10 折痕处Mises应力（单位：Pa）

综上，线路线形对有折痕的DI 弹条受力影响更大。由工况1、工况2、工况7、工况8 的计算结果可知，弹条在小半径曲线地段服役时，折痕处应力均超过屈服强度，弹条在列车荷载下断裂风险更大。同种线路情况下，列车运行速度越快，弹条受力越大，当列车运行速度在100 km/h 以下时，弹条虽有折痕但也没有疲劳断裂风险；当列车运行速度大于等于120 km/h 时，有折痕的弹条有一定断裂风险。

4 结论及建议

本文在建立DTⅥ2 型扣件有限元模型的基础上，分别建立了无折痕、有折痕情况下的弹条模型，代入扣件有限元模型并进行动力学仿真计算。得出以下结论：

1）DI弹条无折痕时，12种工况下，最大Mises应力均出现在前拱小圆弧内侧，未达到弹条材料的屈服强度，弹条整体为安全状态，没有发生断裂的风险。

2）弹条存在初始缺陷折痕时，12 种工况下，折痕位置均出现应力集中，小半径曲线地段以及列车运行速度大于等于120 km/h 地段服役的弹条，在折痕处最大Mises 应力优先超过屈服强度，存在断裂风险，这与实际情况相吻合。

3）弹条生产厂家应调整生产工艺，消除弹条出厂的初始缺陷，确保弹条形状平滑，可以有效避免弹条发生异常断裂的情况发生，对于提高弹条的使用寿命是有利的。