基于主动吸气控制的双幅钢箱梁涡激振动数值模拟研究
董国朝, 曾梦竹, 韩 艳, 许育升, 吴肖波, 罗楚钰
(1.长沙理工大学 土木工程学院,长沙 410114;2.桥梁结构健康与安全国家重点实验室,武汉 430034;3.长沙理工大学 国际工学院,长沙 410114)
作为连续梁桥常用的一种断面形式,钢箱梁具有典型的钝体气动外形,易引起主梁的涡激振动现象。此外,为提高桥梁的通行能力,国内外越来越多的平行双幅桥已投入建设运营。不同于单幅桥梁,双幅桥梁的上、下游幅之间存在一定的“气动干扰效应”,致使涡激振动响应被放大[1-2]。因此,有必要开展双幅钢箱梁桥涡激振动机理及控制研究。
针对大跨度桥梁的风致振动问题,在已有的研究中提出了机械控制措施和流动控制措施。机械控制措施包括主动控制和被动控制两种。被动控制无需外部能量,常用的被动控制方法有调谐质量阻尼器(tuned mass damper,TMD)和电涡流阻尼器等。Larsen等[3]设计了调谐质量阻尼器来控制丹麦大带东桥(Great Belt East Bridge)的风致振动,取得了较好的控制效果。随后,TMD又被用于控制特罗伊大桥的涡激振动[4-5],结果表明,主动控制下的TMD在减小和控制涡激振动响应方面具有较好的效果。但目前TMD往往只能控制单一模态,无法适应多阶涡激振动问题。
流动控制措施是指通过改善结构绕流场特性从而抑制涡激振动的方法[6]。按照是否需要外部供能可分为被动方式与主动方式两种。被动方式是目前控制涡激振动广泛使用的抗风措施,通常通过对原始断面外形或其附属设施(如护栏、检修轨道、风障等)的位置、样式等进行调整[7-9],以找到合适的组合形式,或者通过附加某些气动措施,如稳定板、导流板、抑流板、风嘴等[10-12],提高断面的涡激振动性能。Chen等[13-15]通过节段模型风洞试验研究了被动吸/吹气对桥梁涡激振动的控制效果,发现被动吸/吹气产生的流向涡能够减小展向涡强度,竖向涡激振动基本被完全抑制,对扭转涡激振动也有很强的抑制效果。由于桥梁断面绕流复杂性,各类气动外形优化措施均难以具备涡激振动控制的普适性。另外,被动流动控制是事先给定的,不能根据流动环境的改变进行相应的调整。
主动流动控制方法通过在流场中注入合适的扰动,使之与流动的内在模式相互耦合达到控制涡激振动的目的。主动流动控制的气动措施包括结构表面运动、吸/吹气流动控制等,其目标是具有良好的自适应能力,可以根据工况的变化改变自身的结构外形或流动参数,从而达到最优的控制效果。Kim等[16]在静止的圆柱的展向施加了同相和反相两种正弦形式的主动定常吸气控制措施,有效地减小了圆柱的气动阻力和脉动升力。Chen等[17]在圆柱的主动吸气控制研究中发现,稳定吸气流量控制能够有效地减小圆柱表面压力和非定常的气动力,从而有效地控制了涡激振动。
以上有关涡激振动的主动流动控制措施中,对并列钝体断面的研究较少。本文选取了具有典型特征的双幅钢箱梁断面,运用计算流体动力学(computational fluid dynamics,CFD)方法并结合编写的结构振动程序求解双幅主梁的涡激振动响应,对比风洞试验的结果验证数值模拟方法的可靠性。通过CFD数值模拟技术对双幅钢箱梁的涡激振动进行主动吸气流动控制,并探明主动吸气控制措施的抑振机理。
1 风洞试验
以某三跨钢箱连续梁桥(123 m+178 m+123 m)为背景[18],研究了-3°、0°、+3°风攻角下主梁的涡激振动响应。主梁的跨中横断面如图1所示,上、下游幅主梁间距D为0.5 m,与单幅主梁宽度B之比D/B约为0.038。原断面主梁节段模型风洞试验在长沙理工大学风工程试验研究中心完成,如图2所示。利用有限元分析软件建模计算并获取该桥主梁的模态及振型,动力特性参数如表1所示。风洞试验节段模型的缩尺比为1∶40,试验风速比为1∶3.62。
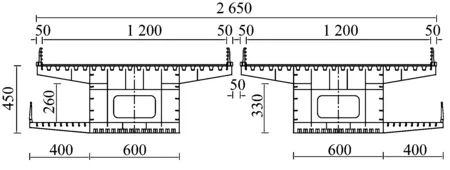
图1 主梁横断面图(cm)Fig.1 Cross section of main beam (cm)

图2 风洞试验节段模型图Fig.2 Segmental model of wind tunnel test
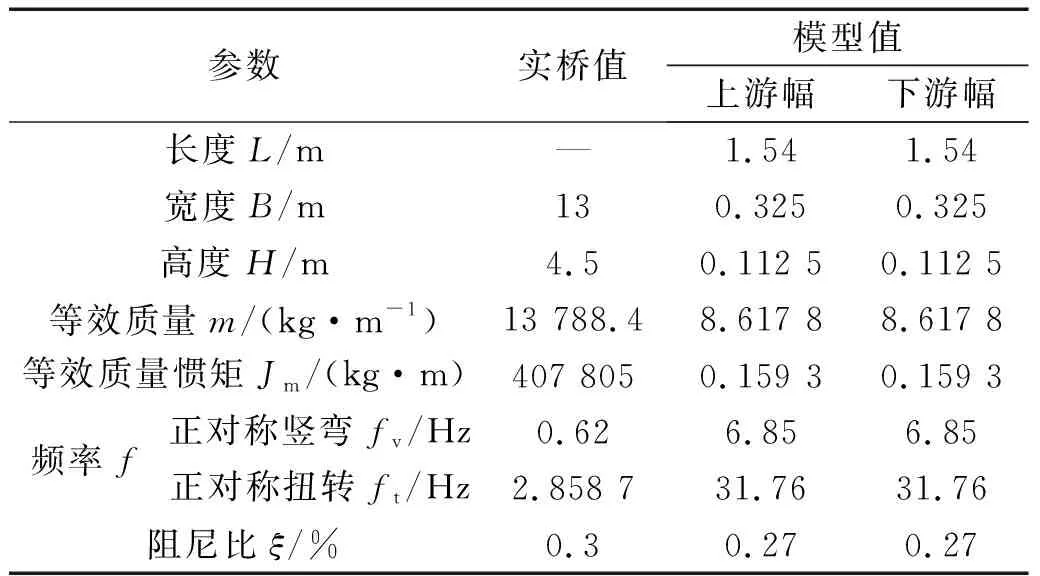
表1 节段模型动力特性参数表Tab.1 Dynamic characteristic parameters of segmental model
原断面主梁无量纲振幅随折减风速的变化,如图3所示。其中,RMS(y)为计算稳定后竖向位移时程曲线的均方根值,H为主梁的高度;折减风速Ur=U/fyH,U为来流风速,fy为正对称竖弯频率,不同的折减风速Ur由改变来流风速U来实现。原断面主梁节段模型风洞试验结果表明:在各风攻角下,上、下游幅主梁均发生了明显的竖向涡激振动现象,且由于上、下游幅主梁的“气动干扰效应”,导致下游幅主梁的涡激振动位移明显大于上游幅主梁的涡激振动位移;试验中未观察到扭转涡激振动现象。
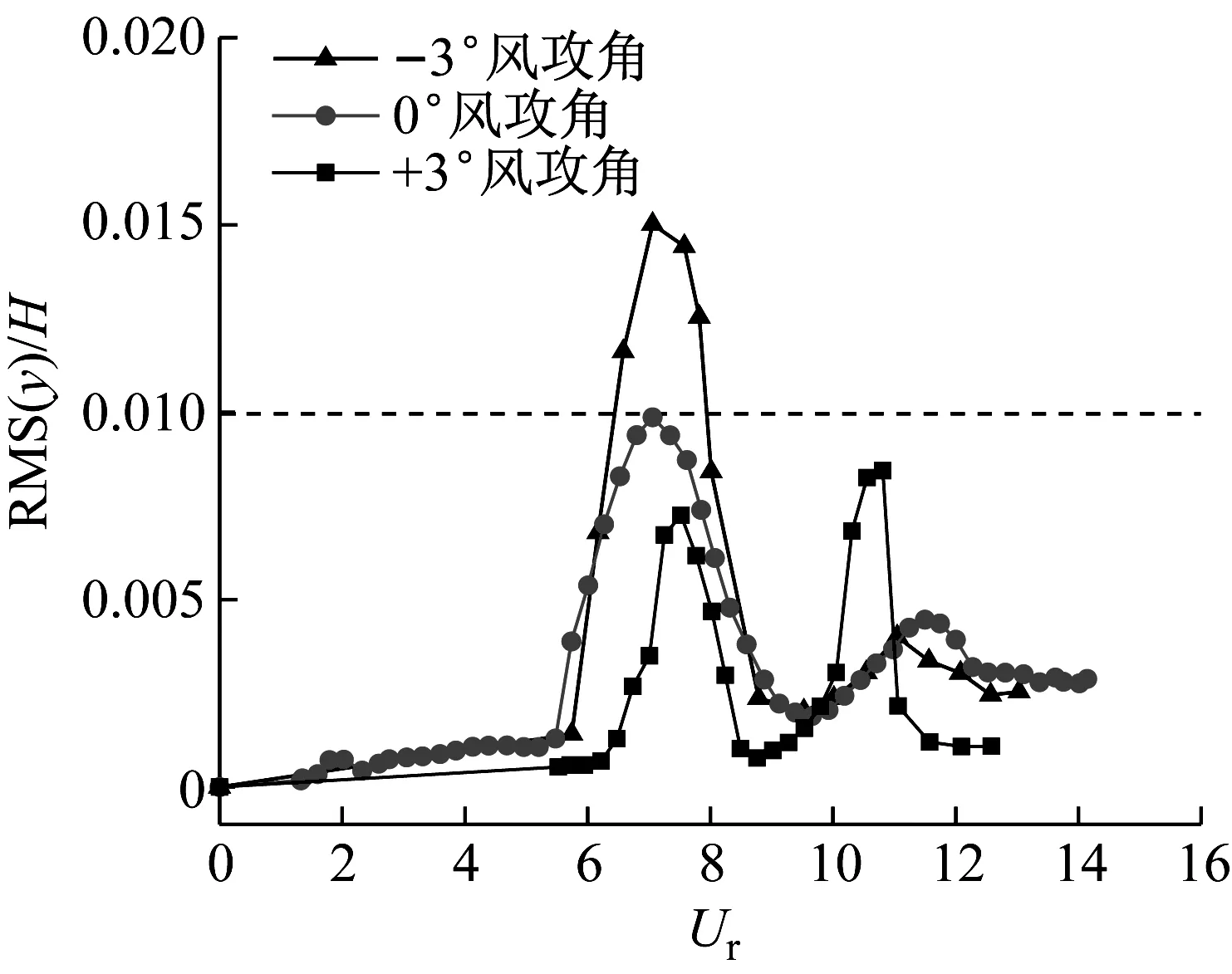
(a) 上游幅
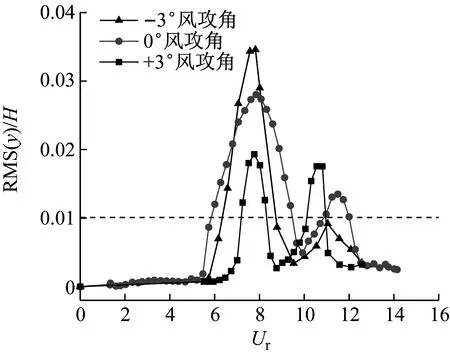
(b) 下游幅图3 无量纲振幅随折减风速的变化Fig.3 Dimensionless amplitude of variation versus reduced wind speed
在各风攻角下,上、下游幅主梁均存在两个涡激振动区间,且同一风攻角下,上、下游幅主梁的两个涡激振动区间值近似。-3°风攻角时,上、下游幅主梁的最大涡激振动位移明显大于+3°和0°风攻角的结果。根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》,-3°风攻角时上、下游幅主梁的涡激振动位移均超过了规范限值。因此,-3°为该双幅钢箱梁最不利风攻角。
2 数值模拟
2.1 数值计算模型及参数
实际双幅钢箱梁桥的主梁为三维结构,且由于桥梁的栏杆、U肋等附属设施与主梁断面的特征尺寸差异较大,采用三维数值模型的网格数量将达到108量级以上。而本文计算还涉及自编程的“动网格”涡激振动流固耦合计算,采用三维模型的数值模拟将耗费巨大的计算资源。在已有研究中,刘小兵[19]采用风洞试验与二维数值模拟计算方法,研究了大跨度双幅桥面桥梁的气动干扰效应。刘志文等[20]采用二维数值模拟方法对宽高比为4的矩形断面的涡激振动进行了数值模拟,计算结果与风洞试验吻合良好。上述研究表明,当前二维数值计算已经具备较好的计算精度,能为科学研究和工程试验提供指导建议。因此,综合考虑计算精度和计算资源,本文采用二维数值模型对双幅钢箱梁断面的涡激振动进行主动吸气控制措施的研究,数值模型比例与风洞试验模型一致,截面几何信息,如图4所示。
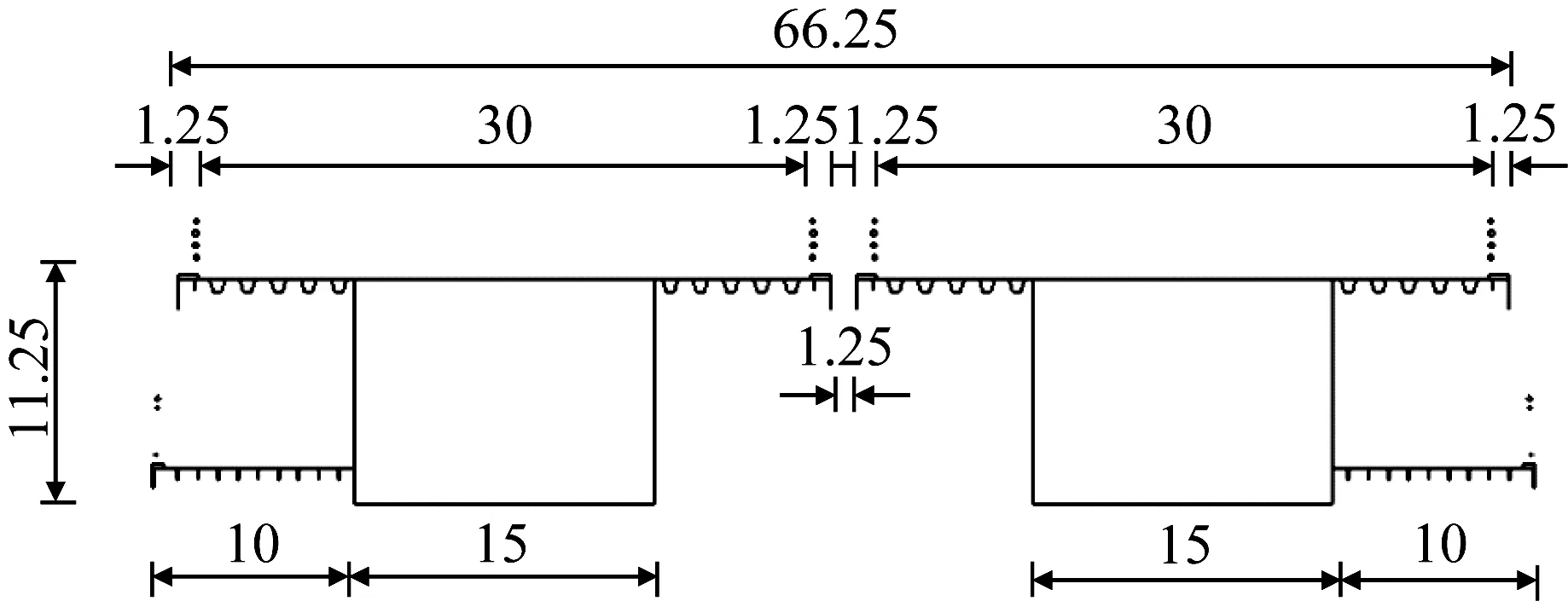
图4 截面几何信息(cm)Fig.4 Sectional geometry information (cm)
假设吸气装置沿桥跨展向通长设置,基于CFD数值方法取长度单位的模型用于研究断面的受力特性[21]。通过观察原主梁断面发生涡激振动时的绕流场特征,初步选定吸气源的布置位置,如图5所示。SLU为上游幅上表面迎风侧栏杆基石处吸气源,SLL-L为上游幅箱梁底部左侧吸气源,SLL-R为上游幅箱梁底部右侧吸气源;SRU为下游幅上表面背风侧栏杆基石处吸气源,SRL-L为下游幅箱梁底部左侧吸气源,SRL-R为下游幅箱梁底部右侧吸气源。实际桥梁上安装的除湿风机管道直径一般不大于0.2 m,对应模型的气孔直径为0.005 m。因此,吸气源宽度D取为0.005 m,D与主梁高度H之比约为0.044,定义D/H为吸气源面积比。对于实际桥梁工程中吸气孔道布置的实施,可以在单位主梁跨度内采用具有相同吸气源面积比的非通长设置方法来实现。
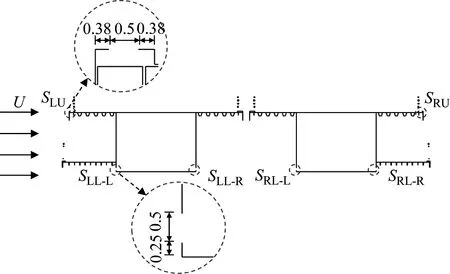
图5 吸气源位置示意及基本参数(cm)Fig.5 Position of the suction slits and its parameters (cm)
网格方案和边界条件示意图,如图6所示。计算区域满足5%以下的阻塞比要求。计算域边界条件为:双幅主梁断面表面为无滑移壁面边界条件;入口边界条件为:UX=Ucosα,UY=Usinα,其中U为来流风速,α为风攻角;下游边界条件为压力出口边界条件,参考压力为1个大气压。吸气源位置采用速度入口边界条件,改变正/负值即可设定吹/吸气[22]。
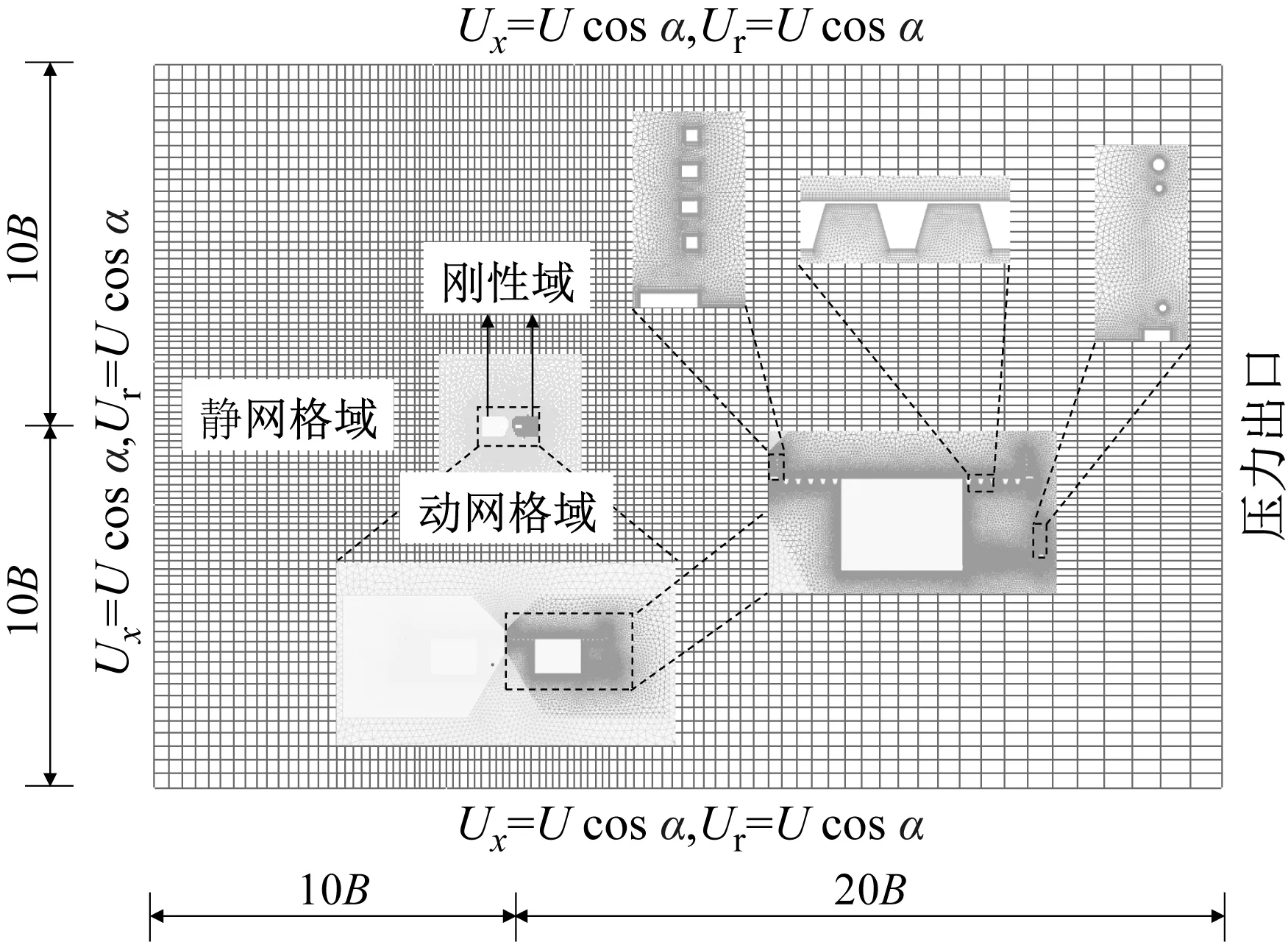
图6 网格方案和边界条件示意图Fig.6 Grid schemes and boundary conditions
本文采用“刚性域+动网格域+静网格域”对计算域网格进行分块处理。在进行网格划分时,首先对主梁断面附近绘制边界层网格,近壁面采用10层结化网格来模拟边界层,第一层网格高度为δ=0.000 2B,增长率为1.08,保证壁面附近网格的精度;在刚性域中采用三角形网格对结构周围区域的网格进行加密,此部分网格伴随结构一起运动;动网格域采用全三角形网格进行划分且按1.08的增长率向外增长,主梁在动网格域内运动;静网格域采用静止的结构化网格进行划分,以提高计算效率。在结构振动过程中,动网格域网格采用网格弹簧光顺(Smoothing)和网格重构(Remeshing)的方法进行重新划分。经网格无关性验证后,选用网格总数约为25万的网格模型,主梁近壁面网格Yplus值控制在1左右。经时间无关性验证后,计算时间步设置为0.001 s,计算残差控制在1×10-6。
2.2 计算方法
二维桥梁断面周围流场采用Fluent求得。湍流模型采用SSTk-ω进行计算,对流项采用二阶迎风格式,瞬态求解格式为二阶隐式。将二维桥梁断面简化为竖弯振动和扭转振动的两自由度弹簧-质量-阻尼系统[23],动力学方程为
(1)
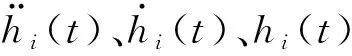
利用“动网格”技术实现主梁断面与流场之间的流固耦合作用。对于某一给定风速,双幅断面的动力响应求解流程图,如图7所示。首先对静止断面进行静态绕流计算,待绕流计算充分后,将断面释放,转化为瞬态求解。在第一个计算时间步之前,静态绕流的初始条件赋值为0。对每一个时间步,先求解流体控制方程(N-S方程),得到速度场及压力场。通过嵌入Fluent中的UDF宏命令Compute_Force_And_Moment提取作用于双幅断面上的升力和扭矩,并将其带入到式(1)右端。采用Newmark-β法求解双幅断面的振动方程,得到断面的振动响应。通过宏命令DEFINE_CG_MOTION将计算得到的竖向速度和角速度赋予上、下游幅主梁断面及对应刚性域网格,动网格域的网格更新后再进行下一时间步的迭代计算。响应稳定后,则停止计算,转入下一个给定风速的数值模拟计算。

图7 动力响应求解流程图Fig.7 Solution flow of dynamic response
2.3 数值计算结果检验
原主梁断面节段模型风洞试验结果中,双幅钝体钢箱梁在-3°风攻角下竖向涡激振动现象最为明显,且未观察到扭转涡激振动现象。为了检验数值模拟计算结果的可靠性,首先计算了-3°风攻角下双幅主梁的竖向涡激振动响应,如图8所示。风洞试验和数值模拟计算结果均表明:上、下游幅主梁均存在两个涡激振动区间,且上、下游幅主梁的两个涡激振动区间值近似。下游幅主梁涡激振动位移大于上游幅主梁涡激振动位移。数值模拟中典型工况(Ur=8.96时,即下游幅主梁振幅最大时)上、下游幅主梁振动稳定后的位移时程曲线如图9所示。两幅桥面的位移时程曲线类似于正弦波,并且下游幅主梁的振动幅值要大于上游幅主梁。
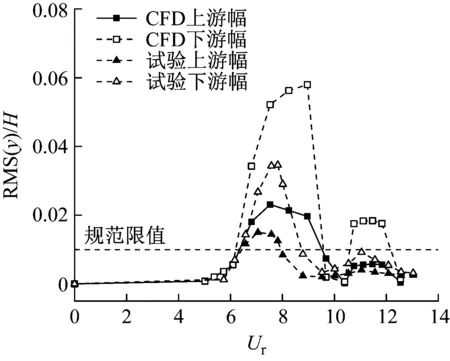
图8 无量纲振幅随折减风速的变化Fig.8 Dimensionless amplitude of variation versus reduced wind speed
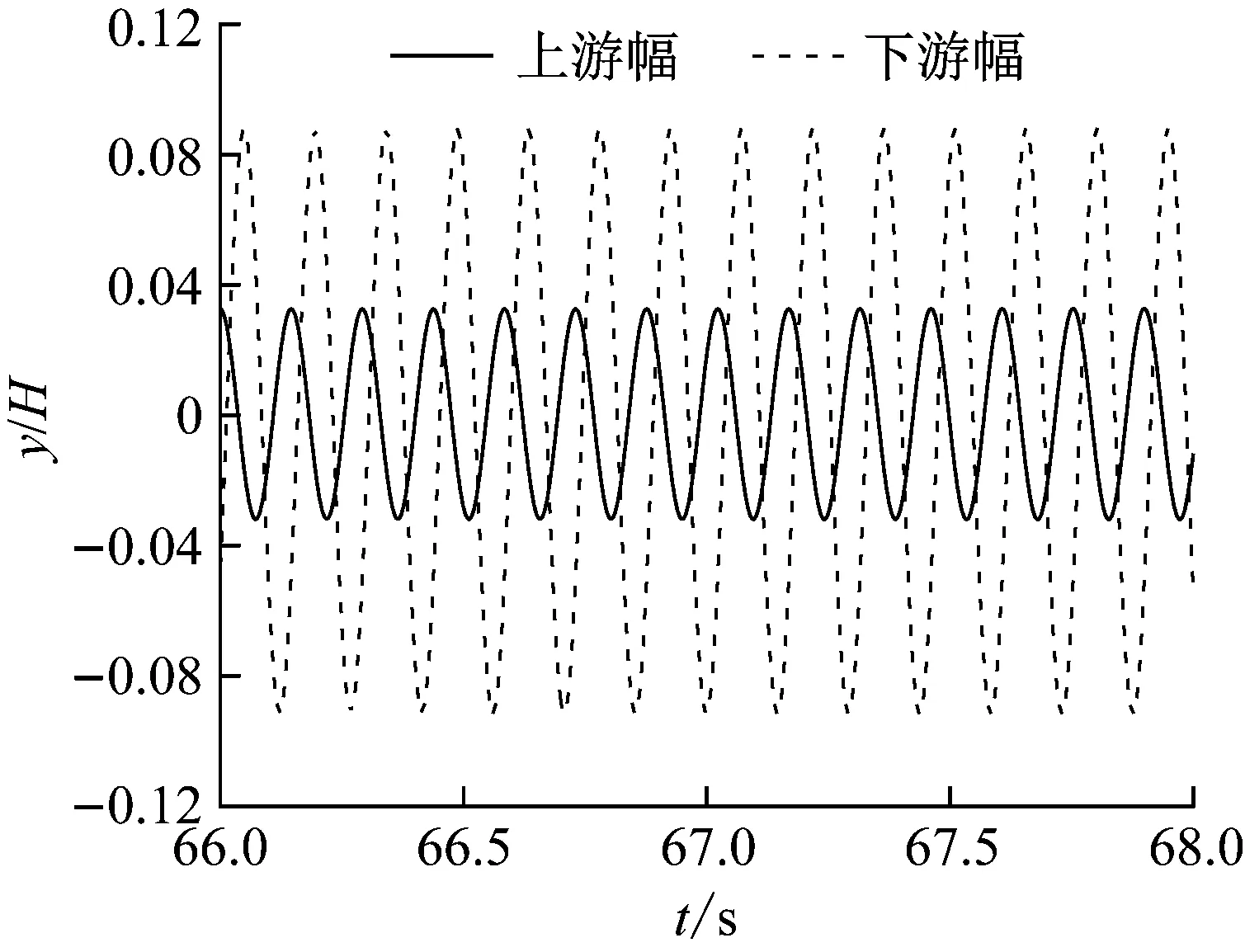
图9 无量纲位移时程曲线(Ur=8.96)Fig.9 Time history curves of dimensionless displacement (Ur=8.96)
对比风洞试验和数值模拟计算结果发现:数值模拟方法能较为准确地捕捉到双幅主梁的涡激振动区间,而通过数值模拟计算得到的涡激振动位移较风洞试验的结果偏大。造成这一差异的主要原因是,本文计算的数值模型为简化后的二维模型,忽略了“三维效应”。杜远征[24]通过对比二维模型与三维模型圆柱绕流的数值模拟结果,探讨了涡激振动中流场的“三维效应”问题,发现尾流的三维效应限制了流体力的增长,减小了圆柱涡激振动的振幅。王林凯等[25]基于OpenFOAM软件采用了三种不同的二维雷诺平均湍流模型(SSTk-ω,k-ε和k-ω模型)对宽高比为5的二维矩形断面进行了静态绕流及涡激振动模拟,对比结果发现SSTk-ω湍流模型的数值计算结果与试验结果最为吻合,但其计算的涡激振动位移相比试验结果依旧偏大。结合数值模拟涡激振动响应的计算结果较风洞试验结果偏大的特点,采用二维数值模拟方法计算主动吸气控制措施对涡激振动的抑制效果是可靠的,且计算结果更为保守。此外,数值模拟的涡激振动折减风速区间及位移随折减风速的变化趋势与风洞试验结果较为吻合。因此,通过对比数值模拟结果和风洞试验结果,验证了采用二维数值模拟方法检验抑振措施的效果具有有效性。
3 计算结果及分析
3.1 主动吸气措施
按照吸气源的布置位置及吸气气流速率的大小,控制工况信息,如表2所示。其中,Us/U为吸气气流速率与来流风速大小的比值。caseI为原主梁断面无控制措施时的工况;caseII、caseIII、caseIV工况Us/U=1.0~2.0(增量为0.5);caseV、caseVI、caseVII工况Us/U=2.0~3.0(增量为0.5)。
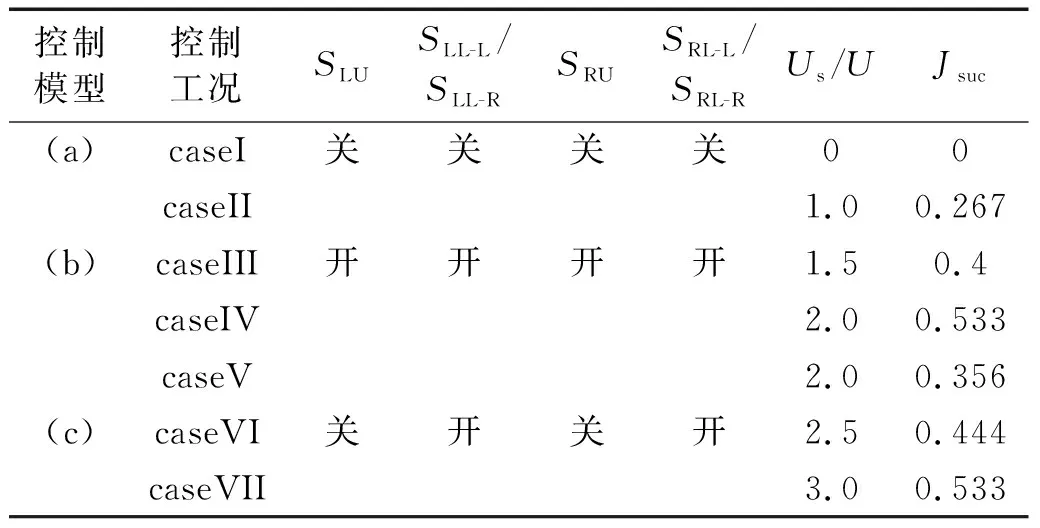
表2 控制工况信息Tab.2 Control condition information
为评估不同控制工况的抑振效果,本文定义了无量纲吸气动量系数Jsuc。无量纲吸气动量系数越小,表明所需注入的外部能量越低。无量纲吸气动量系数Jsuc定义为
(2)
式中:i为吸气源数量;D为吸气源宽度;H为主梁高度。
3.2 数值计算结果对比
采用数值模拟方法对-3°风攻角下主梁的竖向涡激振动进行了主动吸气控制,研究该控制措施对涡激振动的抑制效果并进行相关机理分析。无控工况与各控制工况下主梁无量纲振幅随折减风速的变化曲线,如图10所示。各控制工况典型来流风速下(下游幅主梁振幅最大时)的位移时程,如图11所示。与caseI工况类似,两幅桥面的位移时程曲线类似于正弦波,且下游幅主梁的振动幅值要大于上游幅主梁。
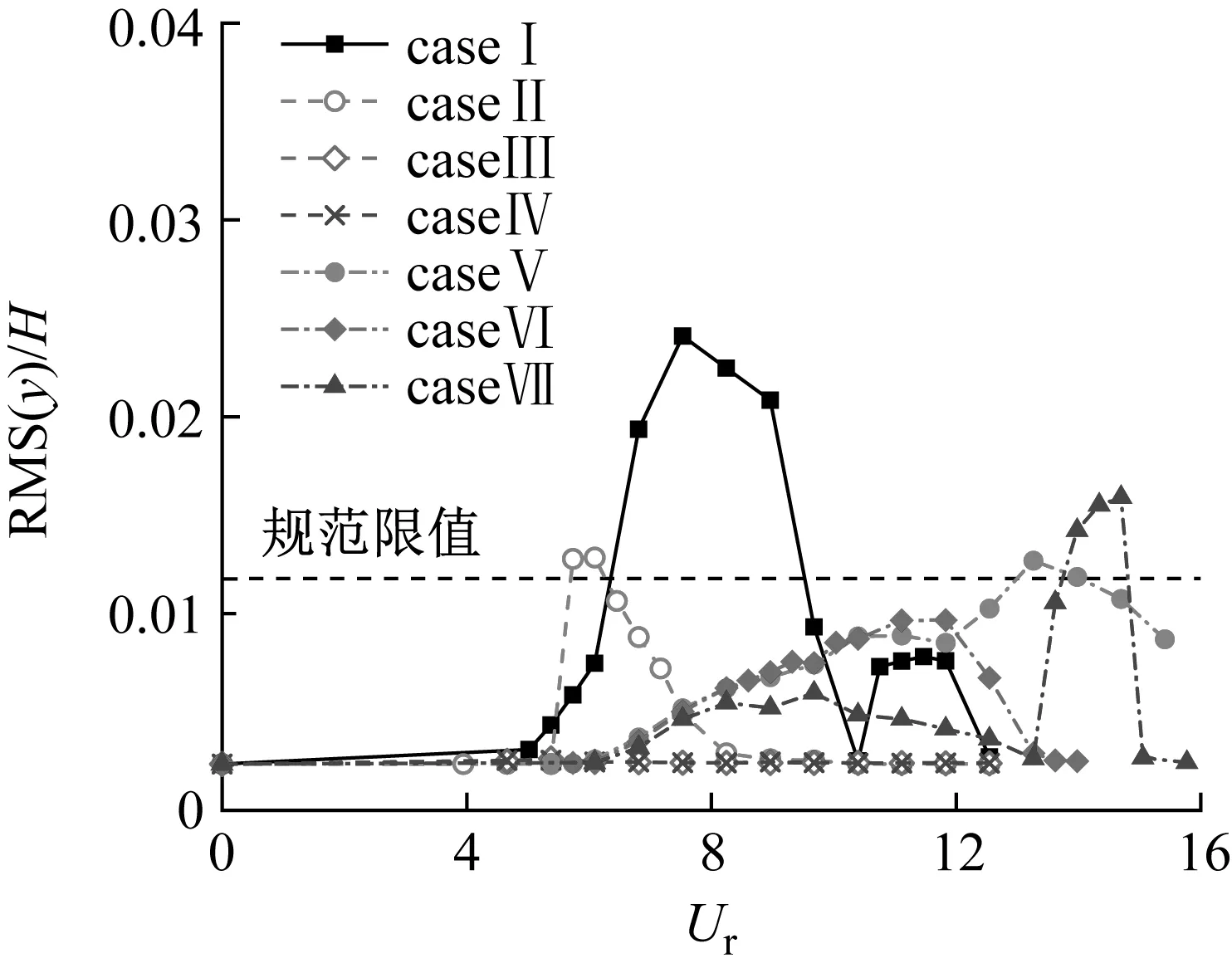
(a) 上游幅
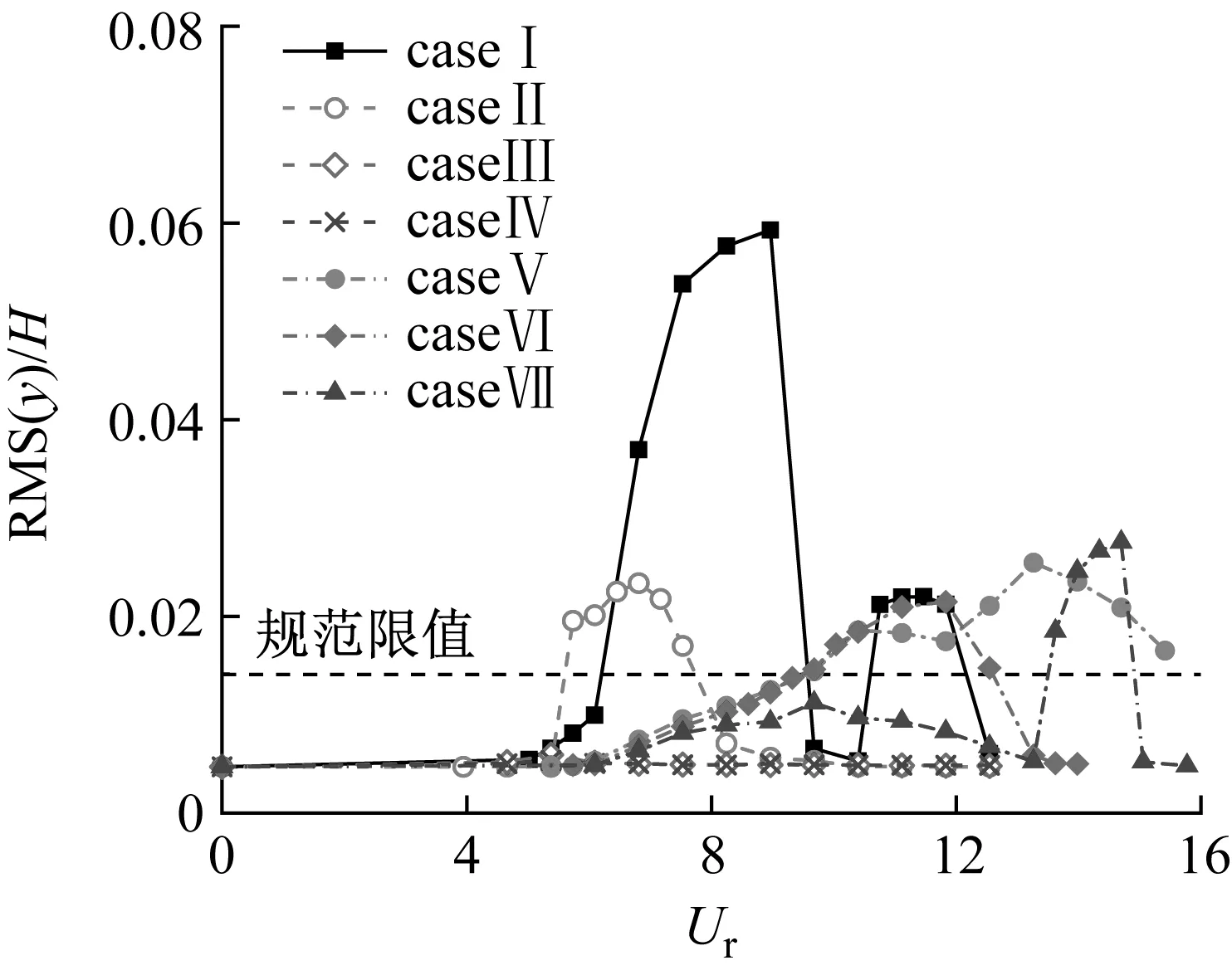
(b) 下游幅图10 无量纲振幅随折减风速的变化Fig.10 Dimensionless amplitude of variation versus reduced wind speed
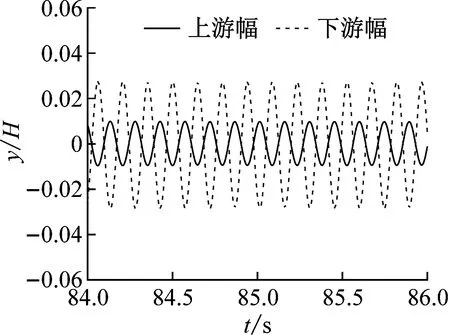
(a) caseII (Ur=6.81)
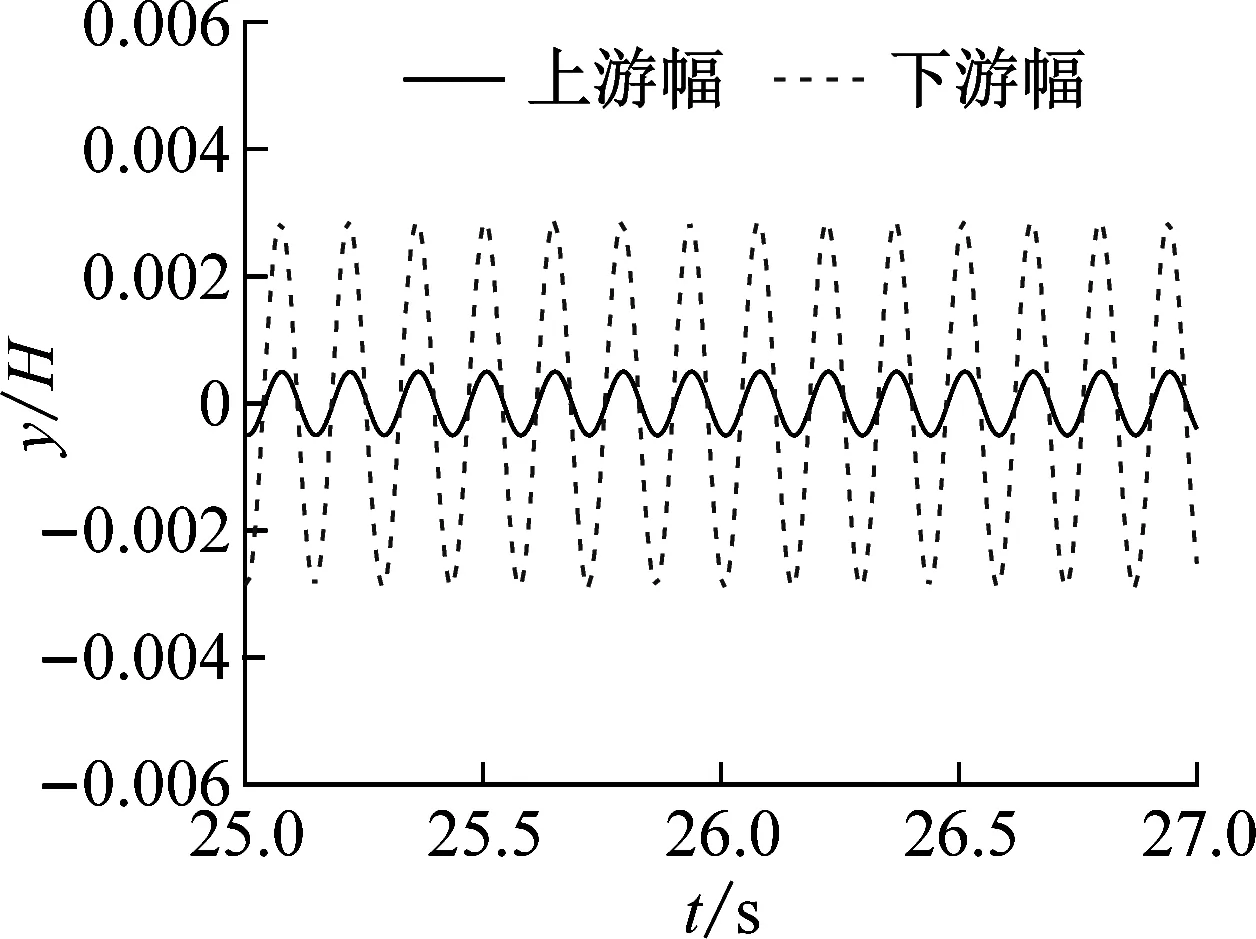
(b) caseIII (Ur=5.38)
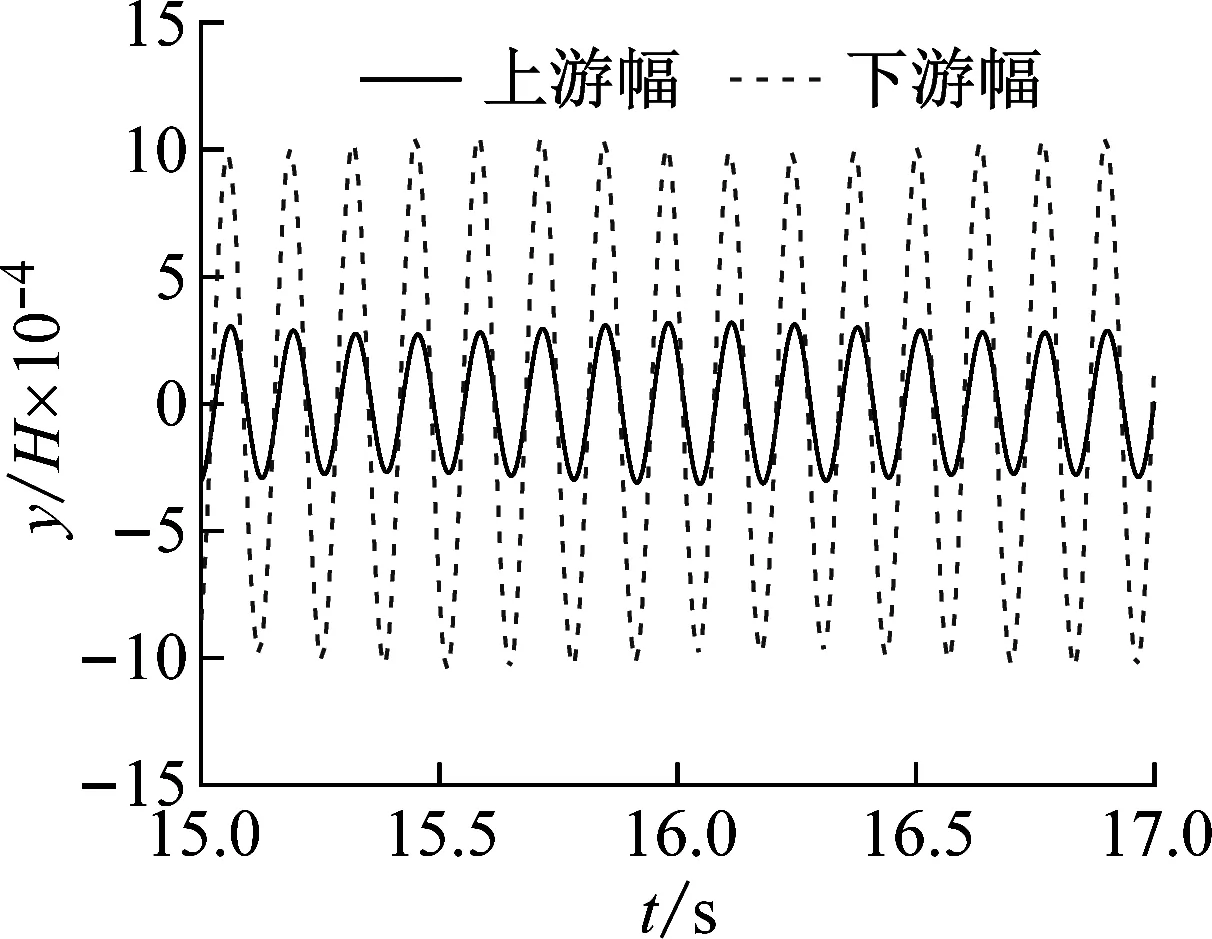
(c) caseIV (Ur=5.38)
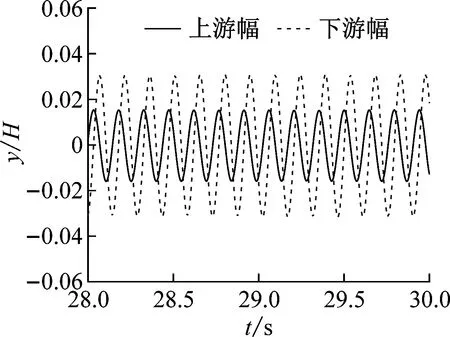
(d) caseV (Ur=13.26)
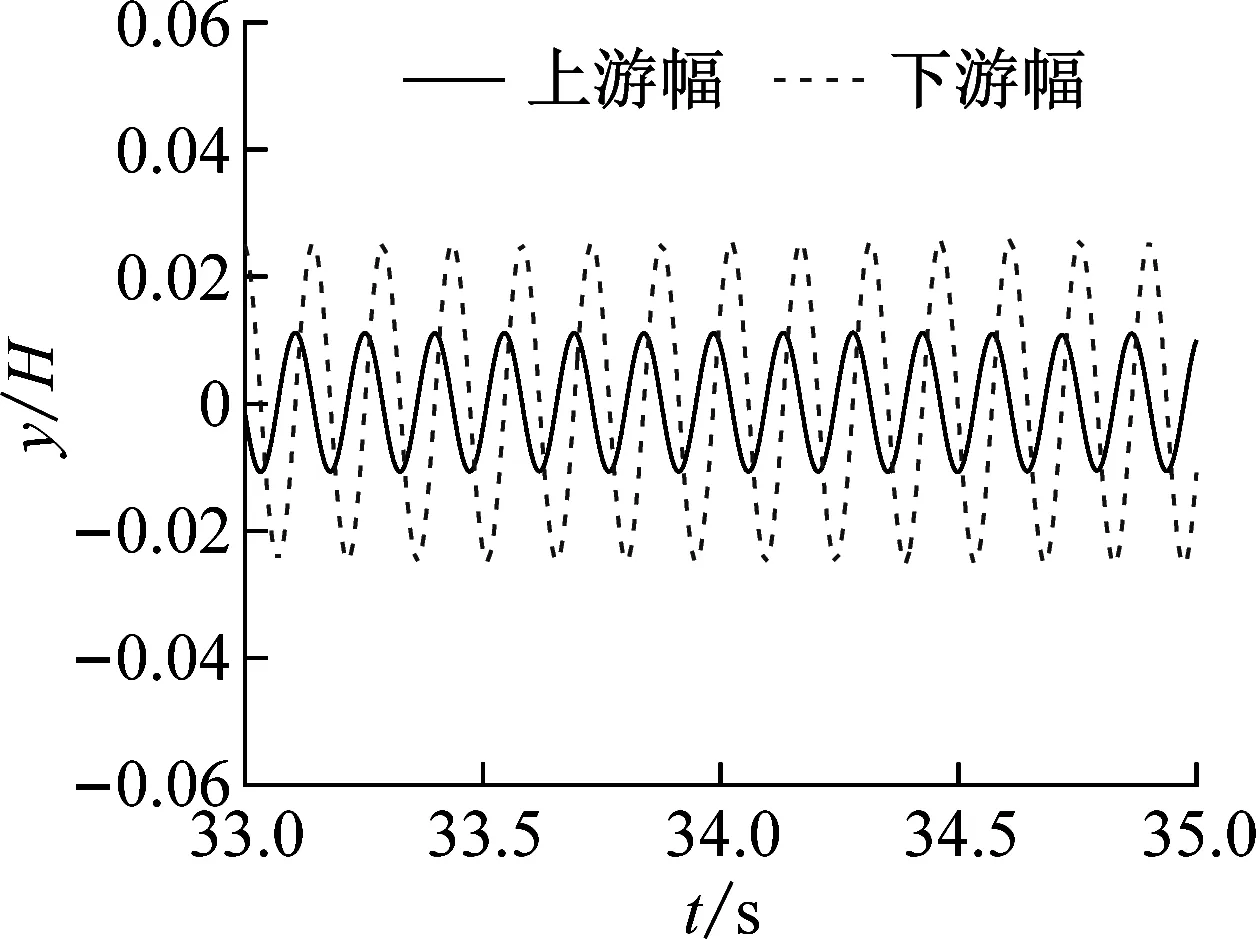
(e) caseVI (Ur=11.83)
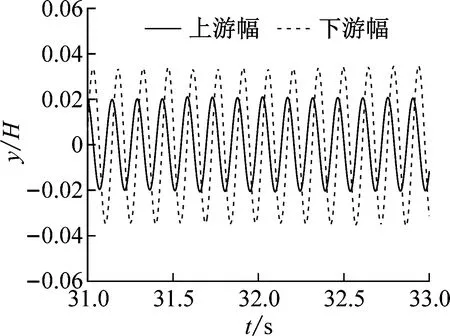
(f) caseVII (Ur=14.69)图11 无量纲位移时程曲线Fig.11 Time history curves of dimensionless displacement
数值模拟控制工况以数值模拟无控工况作为对照组,定义控制工况对主梁断面涡激振动振幅的抑制效果为
α=(Hy-Hi)/Hy×100%
(3)
式中:Hy取原断面涡激振动无量纲振幅最大值;Hi取各控制工况涡激振动无量纲振幅最大值。
由图10,caseI工况上、下幅游主梁的第一个涡激振动区间对应的折减风速为5.73~10.40,第二个涡激振动区间对应的折减风速为10.40~12.55。上游幅主梁在折减风速为Ur=7.53时振幅达到最大,下游幅主梁在折减风速为8.96时振幅达到最大。因此,对于上、下游幅主梁,Hy分别取caseI工况折减风速Ur=7.53、8.96时的涡激振动无量纲振幅。
为了探究表2中控制模型(b)对双幅主梁涡激振动的控制效果,首先计算了吸气气流速率与来流风速大小相同(即Us/U=1.0)时,控制模型(b)的涡激振动响应,即caseII工况的涡激振动响应。caseII工况上、下游幅主梁在折减风速区间5.74~7.53内发生了小幅振动,没有出现第二个涡激振动区间。caseII工况上、下游幅主梁分别在折减风速Ur=6.09、6.81时振幅达到最大值,因此Hi取Ur=6.09、6.81时的涡激振动无量纲振幅。由公式(3)计算可得,caseII工况对上、下游幅主梁涡激振动振幅的抑制效果分别为51.73%、65.80%。caseII工况涡激振动振幅较caseI工况显著减小,但最大涡激振动振幅仍超过了规范限值,不符合规范要求。
考虑到caseII工况对涡激振动的控制有一定效果,进一步增大吸气速率,研究了caseIII、caseIV工况双幅主梁的涡激振动响应。由图10,caseIII、caseIV工况均没有观察到明显的竖向涡激振动现象。对于上、下游幅主梁,caseIII、caseIV工况Hi均取折减风速Ur=5.38时的涡激振动无量纲振幅。caseIII工况对上、下游幅主梁涡激振动的抑制效果分别为98.67%、97.76%,caseIV工况对上、下游幅主梁涡激振动的抑制效果分别为99.18%、98.77%。
对比caseII、caseIII、caseIV工况的涡激振动响应计算结果,随着Us/U增大,主动吸气控制措施对涡激振动的抑制效果越来越好。因此,当Us/U取值合适时,控制模型(b)可有效地抑制双幅主梁的涡激振动。
当减少吸气源的数量而不影响抑振效果时,则能优化主动吸气控制措施。为比较两种控制模型的抑振效果,应保证无量纲吸气动量系数相当。本文计算了控制模型(c)在Us/U=2.0~3.0(增量为0.5)时主梁的涡激振动响应。
caseV工况对原主梁断面第一个涡激振动区间有一定的抑制效果,但对抑制第二个涡激振动区间内的振动效果不佳。由图10可知,caseV工况观察不到两个明显的涡激振动区间,上、下游幅主梁在折减风速区间7.53~15.41内发生了涡激振动。相比于caseI工况,caseV工况上、下游幅主梁发生最大振幅的折减风速后移,在折减风速Ur=13.26时振幅均达到最大值。对于上、下游幅主梁,Hi均取Ur=13.26时的涡激振动无量纲振幅。caseV工况对上、下游幅主梁的抑振效果分别为69.98%、61.96%,且上、下游幅主梁最大涡激振动振幅均不符合规范要求。
与caseV工况类似,caseVI工况也不存在两个明显的涡激振动区间,上、下游幅主梁在折减风速区间7.53~12.55内发生了涡激振动。相比于caseI工况,caseVI上、下游幅主梁发生最大振幅的折减风速后移,在折减风速Ur=11.83时振幅均达到最大值。对于上、下游幅主梁,Hi均取Ur=11.83时的涡激振动无量纲振幅。caseVI工况对上、下游幅主梁涡激振动振幅的控制效果为66.34%、69.28%,仅下游幅主梁最大涡激振动振幅不符合规范要求。
caseVII工况对抑制原主梁断面第一个涡激振动区间内的振动效果较好,仅在折减风速为8.24~13.26发生了小振幅振动,且振幅限值符合规范要求。第二个涡激振动区间对应的折减风速为13.26~15.06,较caseI工况的第二个涡激振动折减风速区间后移,上、下游幅主梁在折减风速Ur=14.69时涡激振动振幅均达到最大值。对于上、下游幅主梁,Hi均取Ur=14.69时的涡激振动无量纲振幅。caseVII工况对上、下游幅主梁涡激振动的控制效果分别为37.66%、58.16%,第二个涡激振动区间的振动响应不符合规范要求。
对比caseV、caseVI、caseVII工况的涡激振动响应计算结果,控制模型(c)提高吸气速率对控制双幅主梁的第一个涡激振动区间的涡激振动具有有利的影响,但对改善第二个涡激振动区间的涡激振动响应效果不佳。
参考表2中无量纲吸气动量系数Jsuc的大小,对比控制模型(b)与控制模型(c)对双幅主梁涡激振动的抑制效果,可知:当无量纲吸气动量系数Jsuc相当时,控制模型(b)的抑振效果更好。此外,吸气气流的速率也会影响对涡激振动的控制效果。在理想的控制模型下,吸气速率越高,对涡激振动的抑制效果越好。若控制模型的选取不合理,提高吸气速率对控制涡激振动有一定的积极作用,但效果不够理想。
4 抑振机理分析
结构发生涡激振动的位移大小与振动系统的能量大小有关。本节将选取-3°风攻角下,无控工况(caseI)和控制工况(caseIV)的双幅主梁,从能量输入机制、流场等角度进行分析,探明主动吸气控制措施对双幅主梁涡激振动的抑制机理。
4.1 能量输入机制
当升力和位移相位差整体呈同相位时,升力的方向与主梁的运动方向相同,振动系统的能量增加,从而导致振动位移逐渐增大。当升力和位移相位差整体呈反相位时,振动位移会减小。caseI、caseIV工况的升力与竖向位移的相位差(φ)随折减风速Ur的变化,如图12所示。可见,随着Ur的增大,caseI工况的上、下游幅主梁均发生了两次“相位切换”,即实现了升力和位移的相位差从“同向”到“反向”的切换。而caseIV工况的上、下游幅主梁升力与位移的相位差φ在各折减风速下均约为180°,升力与位移始终呈反相位。
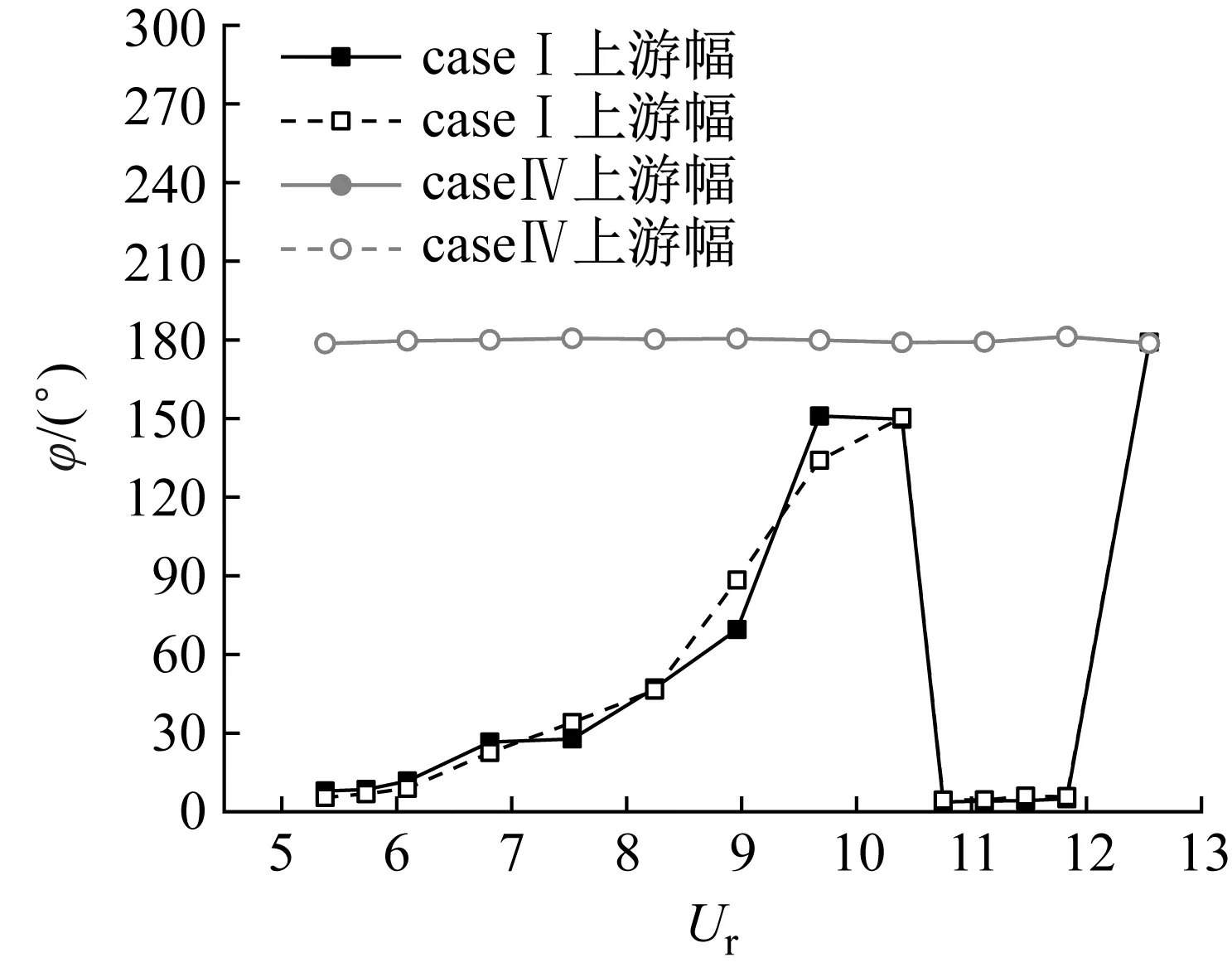
图12 升力与竖向位移的相位差随折减风速的变化Fig.12 Variations of the phase difference between lift force and verticle displacement versus reduced wind speed
主梁振动稳定后单个振动周期中升力对结构做功,振动系统输入的能量值大小为
(4)
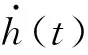
双幅主梁单个周期做功随折减风速Ur变化曲线,如图13所示,涡激力对双幅主梁单个周期做功的变化趋势与双幅主梁无量纲振幅随折减风速Ur的变化相似。caseI工况在涡激振动区间内,涡激力对结构做正功,在涡激振动区间外,涡激力对结构做功近似为零。而caseIV工况在各折减风速下,双幅主梁模型单个周期内升力做功均近似为零。结果表明:主动吸气控制措施使得双幅主梁受到的升力对结构做功显著减小甚至做负功,从而有效地抑制了结构的涡激振动。

图13 单个周期做功随折减风速变化曲线Fig.13 Variation curve of work in a single cycle versus reduced wind speed
4.2 流场分析
以-3°风攻角下,折减风速Ur为8.24时caseI与caseIV工况双幅主梁断面一个振动周期为研究对象,从流场的角度对比分析主动吸气控制措施的抑振机理。双幅主梁断面在一个振动周期内的位移时程曲线,如图14所示。
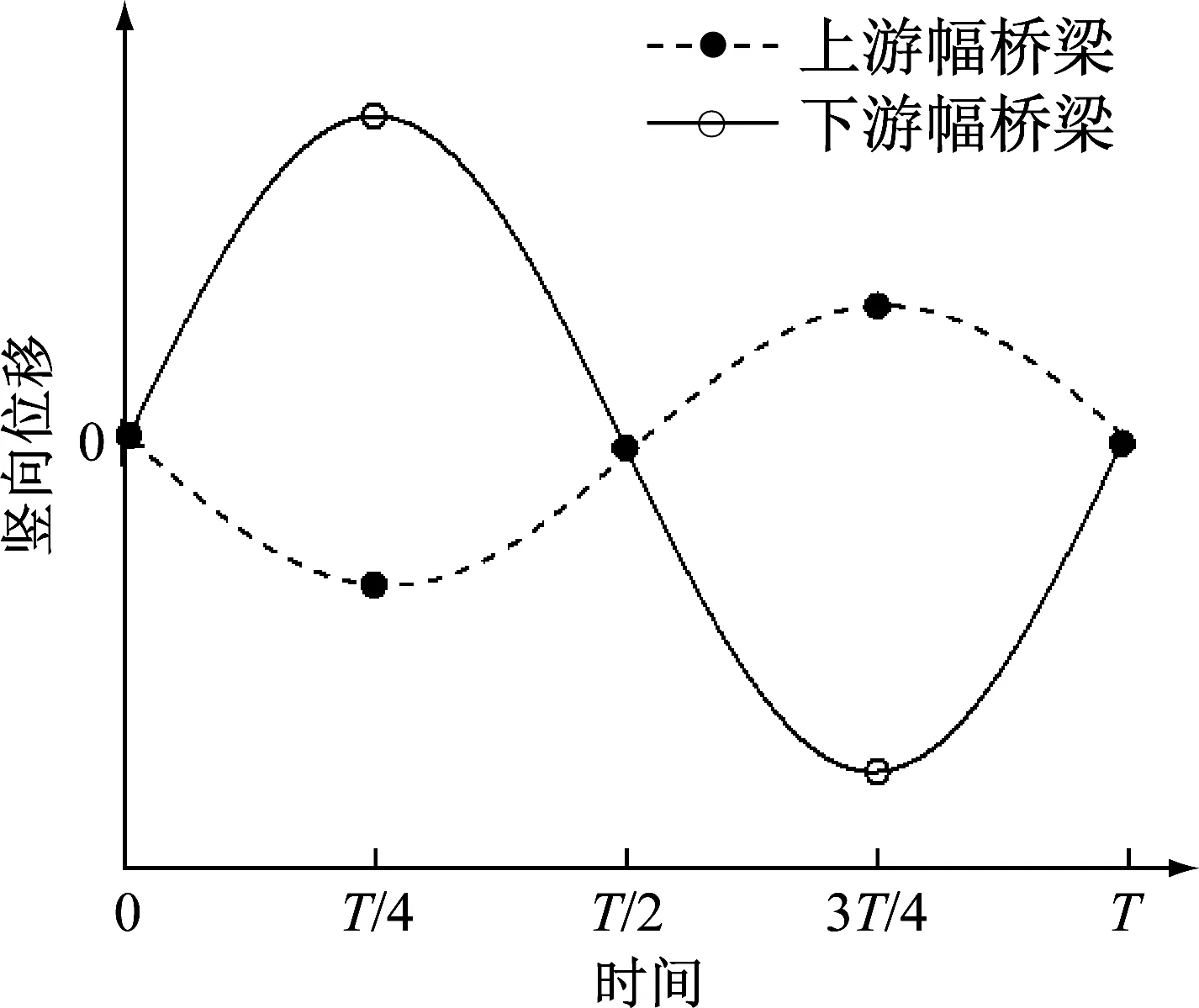
图14 一个振动周期内双幅主梁的位移时程(Ur=8.24)Fig.14 Displacement time-history of double girder in a vibration period(Ur=8.24)
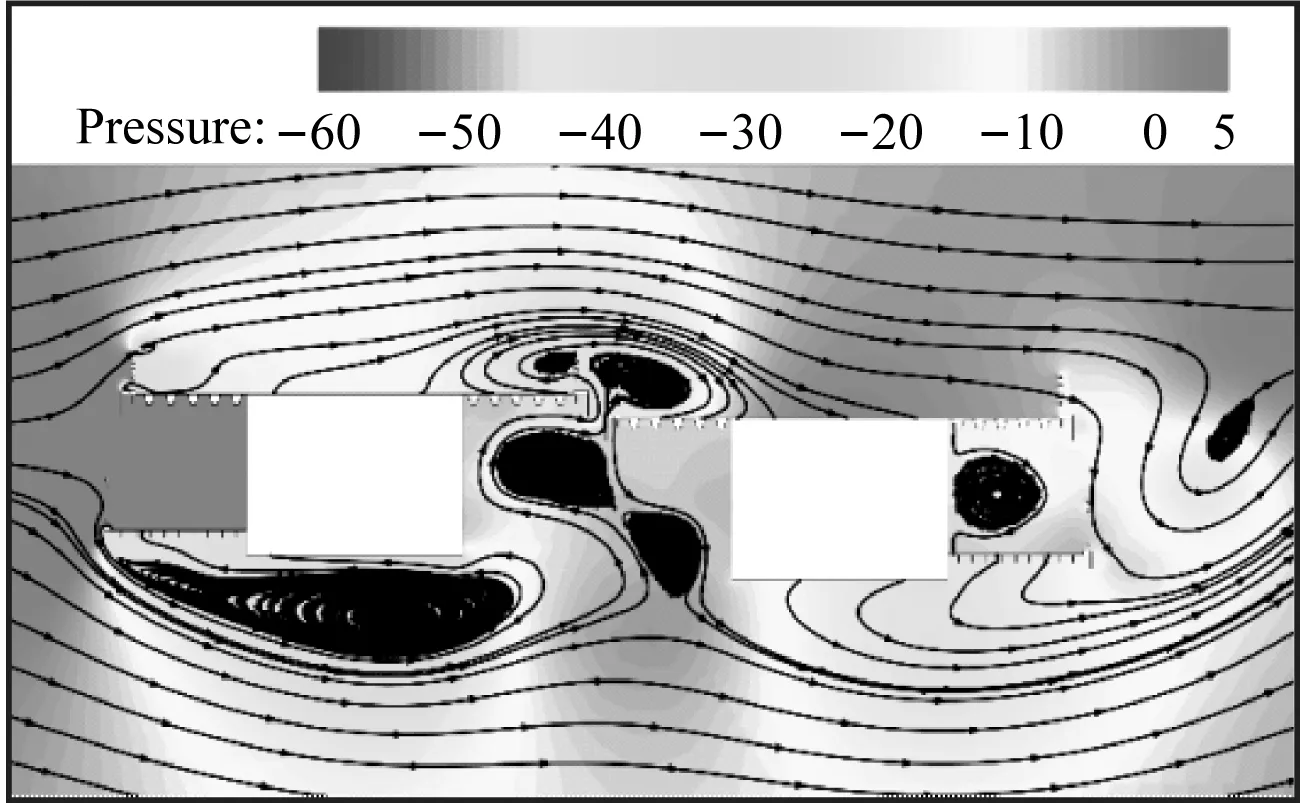
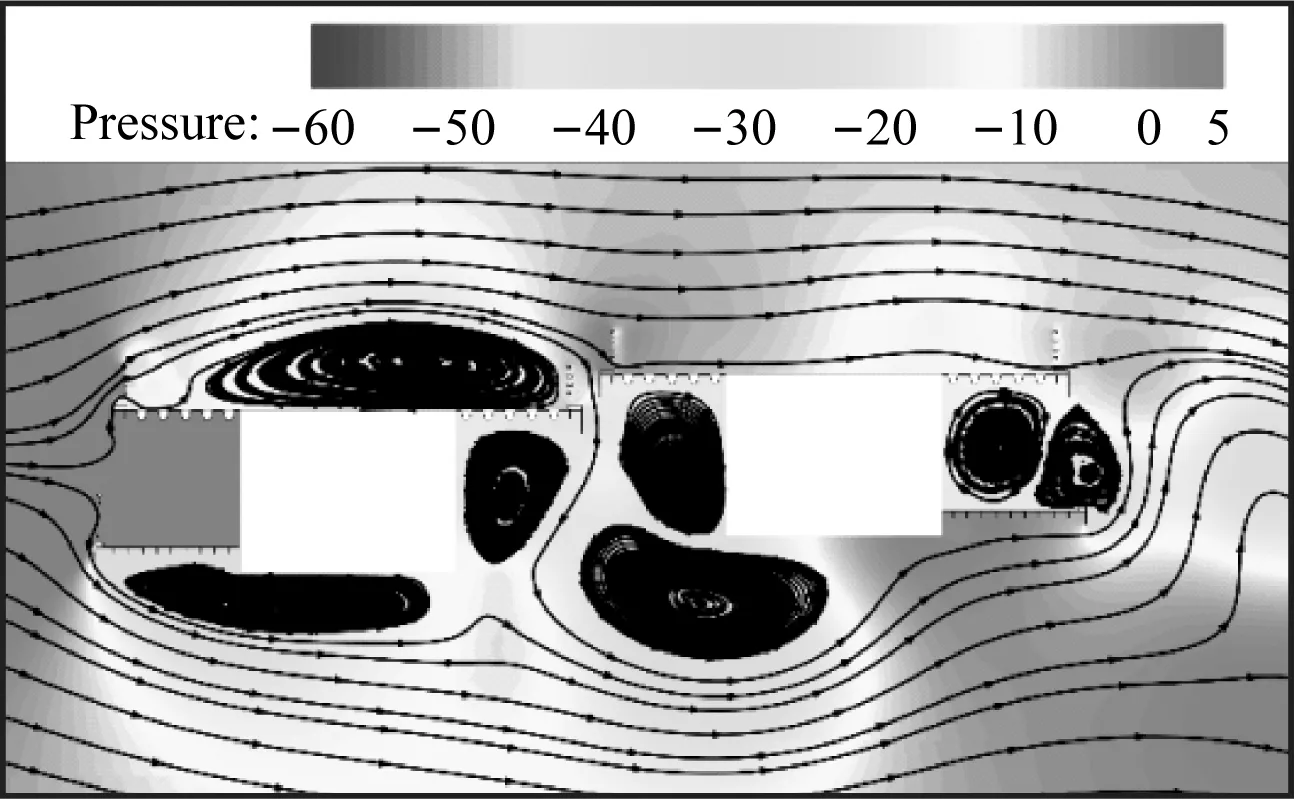
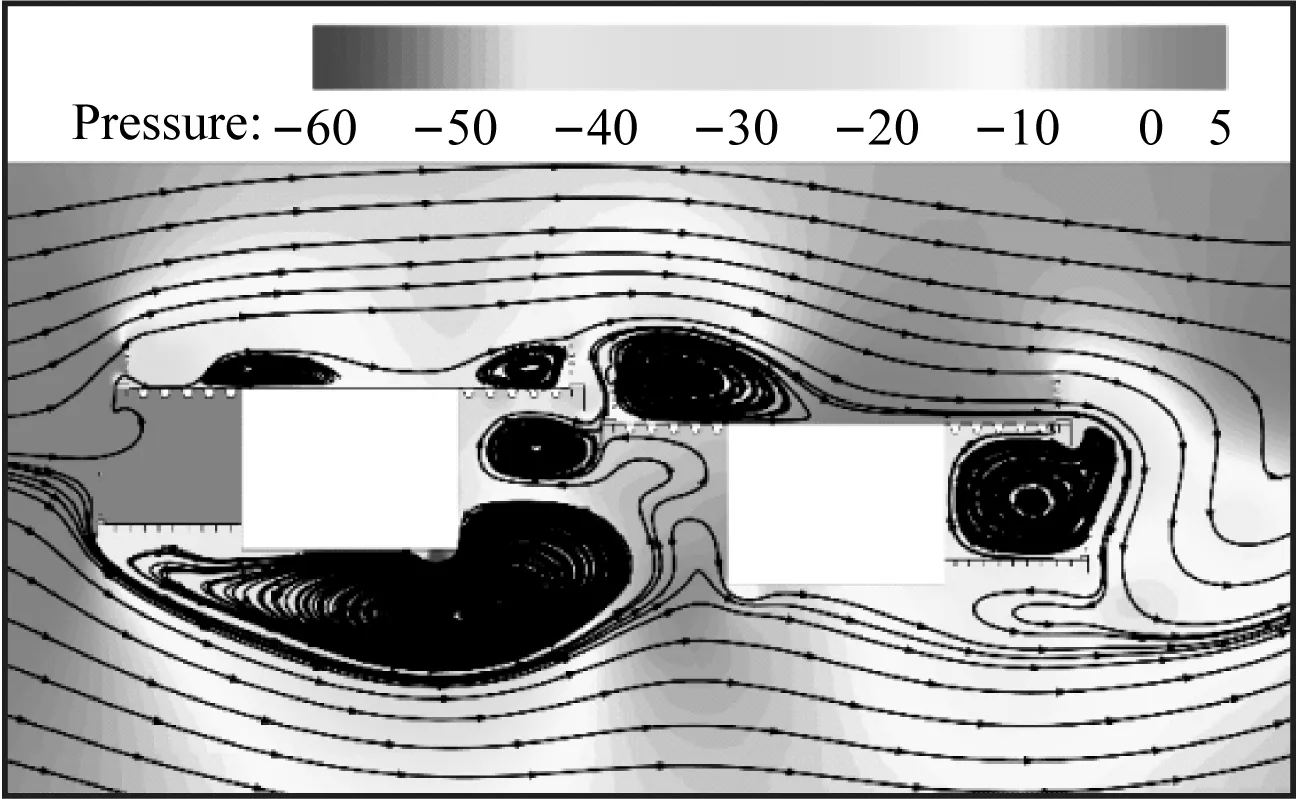
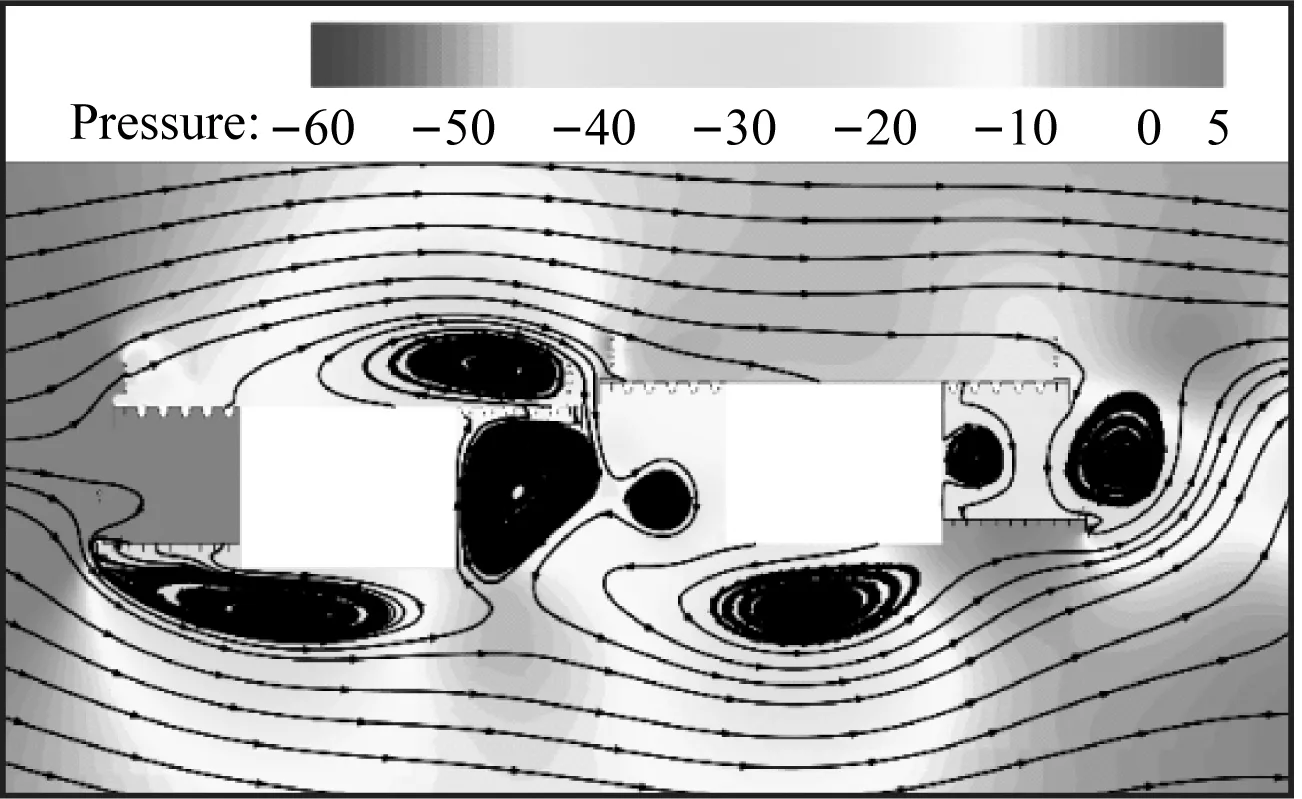
caseI工况双幅主梁断面在一个运动周期内的压力变化如图15所示,双幅主梁上、下表面均形成了尺度较大的涡结构,且由于主梁间间距较小,气流流经两主梁间的通道后在上游幅主梁背风侧及下游幅主梁迎风侧各形成了一个涡结构。旋涡在主梁上、下表面的脱落会导致结构周围的表面压力发生明显的变化。在远端均匀来流风作用下,主梁底面处于负压区,顶面部分处于正压区。来流风在上游幅主梁桥面栏杆及人行道下缘处发生分离,形成旋涡并向下游发展。上游幅主梁人行道下表面前缘形成旋涡并继续向下游发展,主导着上游幅主梁竖直向下运动。随后,旋涡逐渐远离上游幅主梁,此时,背风侧的正压区增强且作用面积增大,推动着上游幅主梁竖直向上运动。上游幅主梁受到旋涡脱落与正压区的交替作用后,诱发了其竖向涡激振动。上游幅主梁上表面栏杆处脱落的旋涡继续向下游发展,受到栏杆的“阻挡效应”后,旋涡的能量增强。下游幅主梁在上表面迎风侧栏杆处脱落的旋涡增强了上表面的主涡。在下表面,上游幅箱梁尾部脱落的旋涡和下游幅主梁迎风侧产生的旋涡相互作用,进一步增强了下游幅主梁下表面的主涡。下游幅主梁受到上、下表面周期性脱落的旋涡交替作用后,诱发了其竖向涡激振动。上游幅主梁发展下来的旋涡对下游幅主梁的气动特性有干扰作用,因此导致了下游幅主梁的涡激振动位移大于上游幅主梁的涡激振动位移。
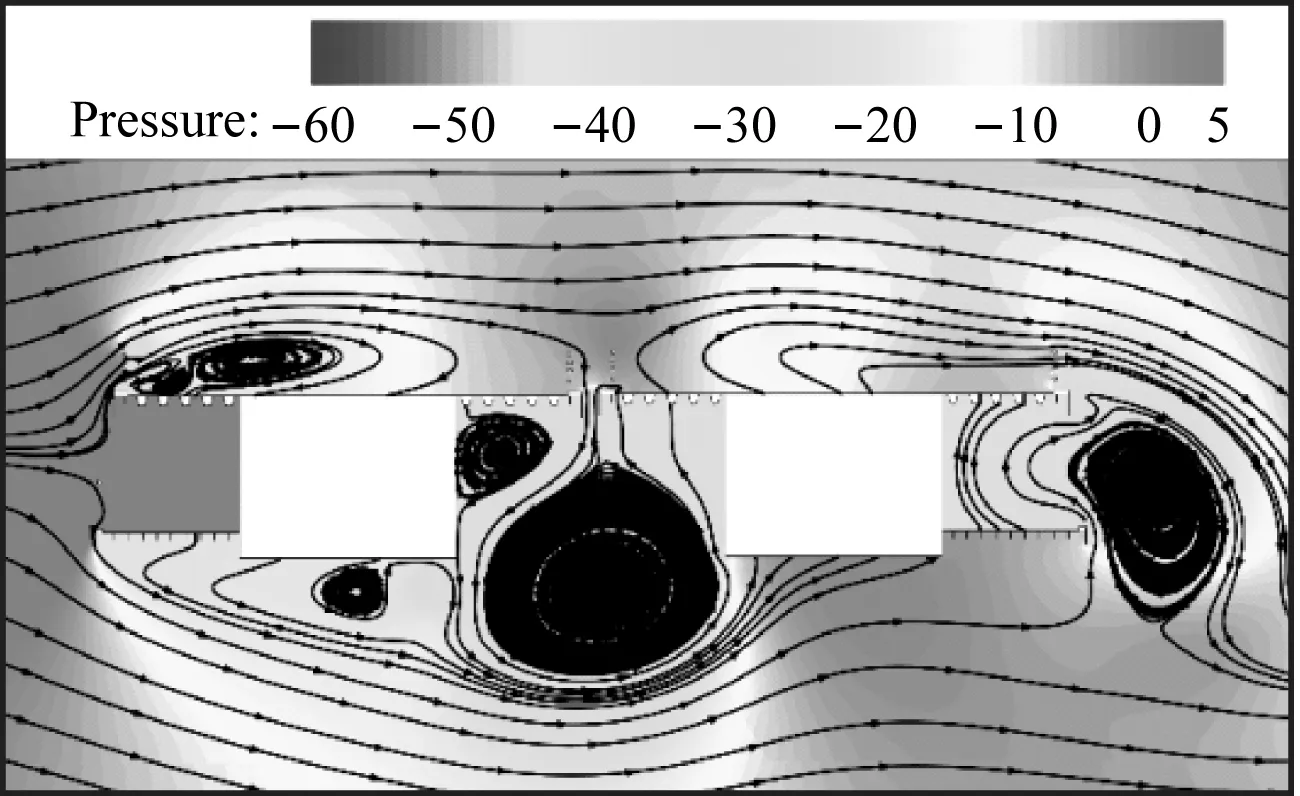
(a) T
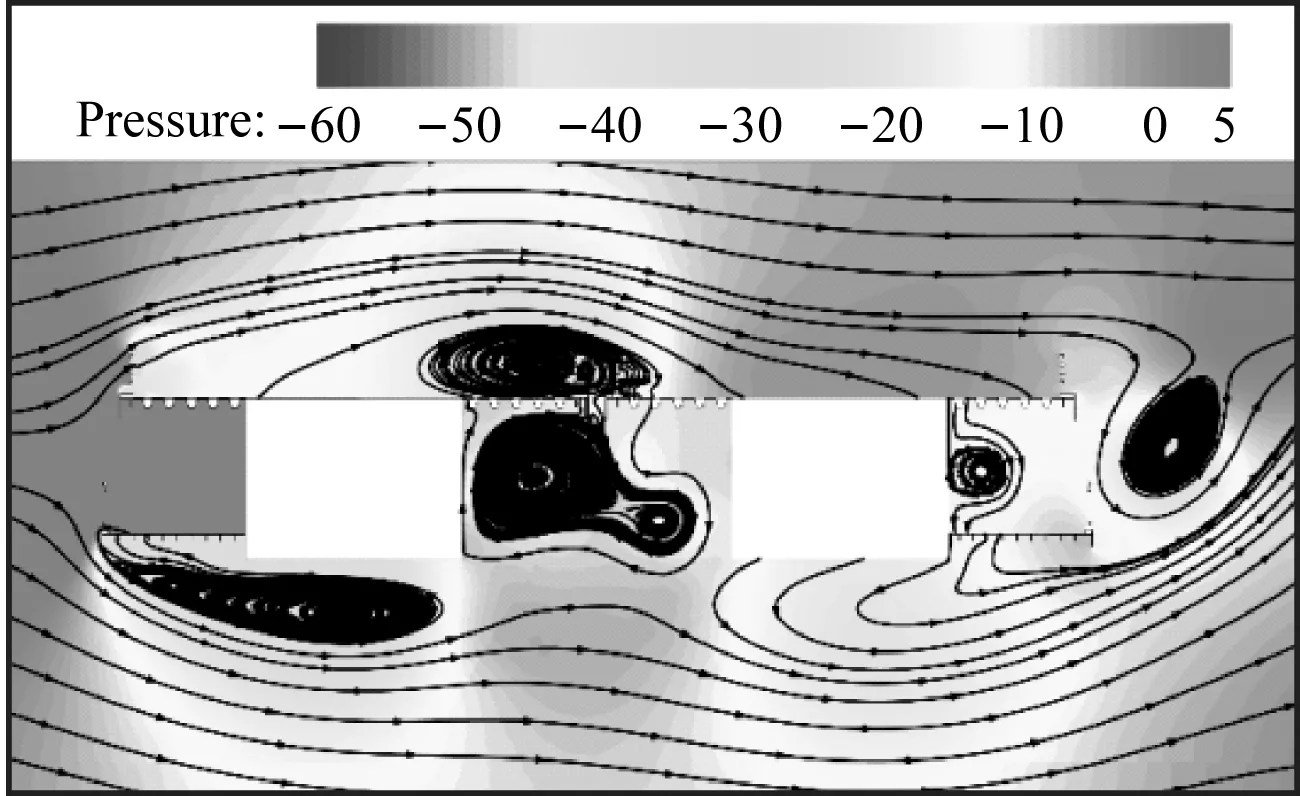
(b) T+T/8
(d) T+3T/8
(e) T+4T/8
(f) T+5T/8
(g) T+6T/8
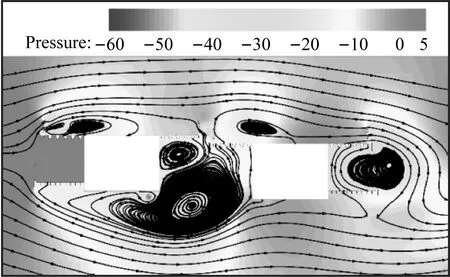
(h) T+7T/8图15 一个运动周期内的压力变化(Pa,caseI, Ur=8.24)Fig.15 Static pressure in a movement period (Pa, caseI, Ur=8.24)
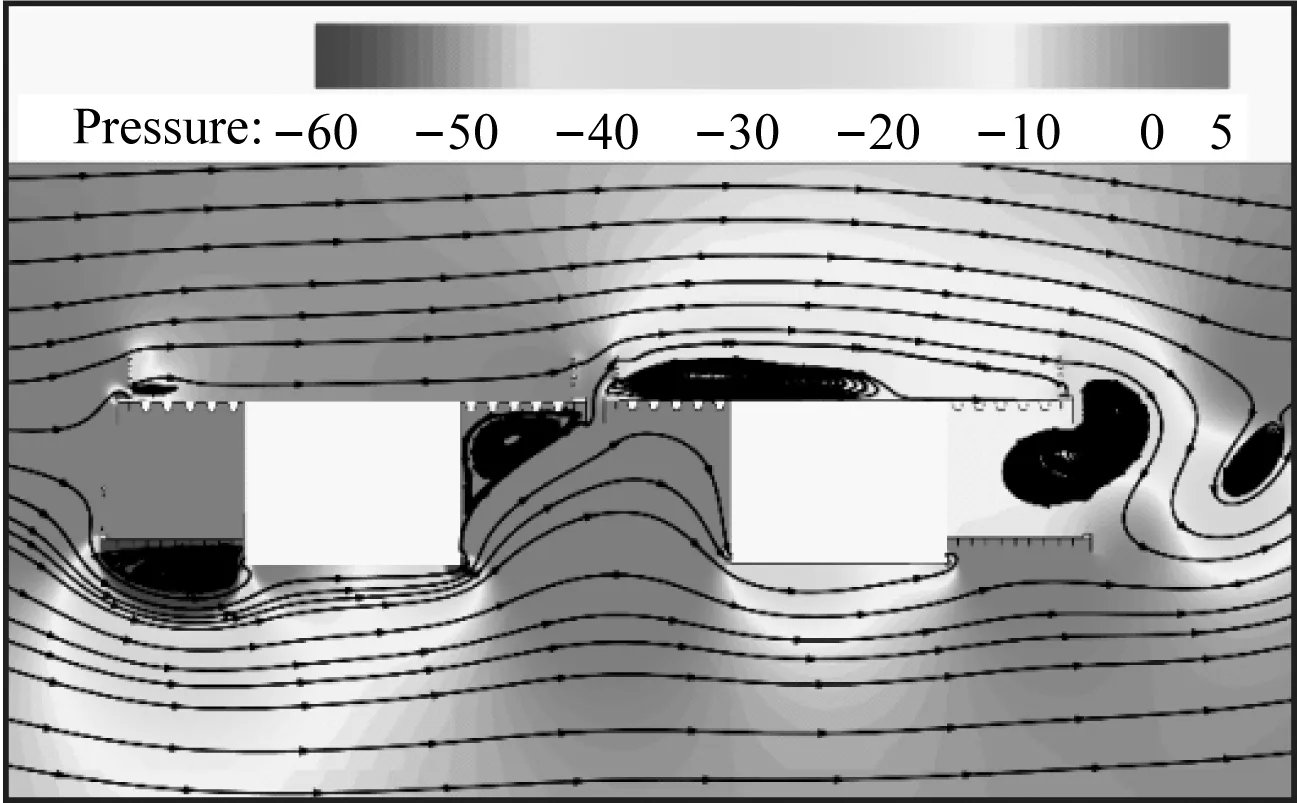
为方便流场可视化,caseIV工况与caseI工况云图中压力梯度保持一致。caseIV工况一个振动周期内的绕流场如图16所示,吸气口附近局部流场呈现为较强的负压状态。在吸气气流作用下,上游幅主梁上表面迎风侧栏杆处基本不会形成旋涡脱落。上游幅主梁下表面在迎风侧形成的旋涡被上游幅箱梁底部左侧吸气源吸收了大部分能量,被削弱后的旋涡向下游发展后被上游幅箱梁底部右侧的吸气源吸收。由图16可知,吸气气流使得上游幅主梁下表面绕流场负压区的压强增大,主梁上、下表面的压强差减小。上游幅主梁受到吸气气流的作用后,不再受到脱落的旋涡和正压区的交替作用,进一步减弱了对系统能量的输入,从而达到了显著抑制上游幅主梁涡激振动的效果。下游幅主梁上表面迎风侧栏杆处脱落的旋涡能量较低,旋涡继续向下游发展后被上表面背风侧栏杆基石处的吸气气流吸收,旋涡大部分能量被消耗。在下表面,上游幅主梁的涡激振动得到有效控制后,基本不会对下游幅主梁的气动特性产生干扰作用。下游幅箱梁底部左侧吸气源吸收了部分能量,余下能量较小的旋涡继续向下游发展,后被右侧吸气源吸收。吸气气流使得下游幅主梁不再受到周期性脱落的旋涡作用,从而有效控制了下游幅主梁的涡激振动。

(a) T

(b) T+T/8

(c) T+2T/8
(d) T+3T/8

(e) T+4T/8

(f) T+5T/8

(h) T+7T/8图16 一个运动周期内的压力变化(Pa, caseIV, Ur=8.24)Fig.16 Static pressure in a movement period (Pa, caseIV, Ur=8.24)
5 结 论
针对气动特性较差的双幅钢箱梁断面,本文提出了两种主动吸气控制模型用来抑制双幅主梁的涡激振动。利用“动网格”技术实现数值模拟中主梁断面与流场之间的流固耦合作用,从能量输入机制、流场等角度分析了主动吸气控制措施的抑振机理。主要结论如下:
(1) 数值模拟结果与风洞试验结果均表明,-3°风攻角下双幅主梁发生了明显的竖向涡激振动。数值模拟的涡激振动区间及位移随折减风速的变化趋势与风洞试验的变化趋势吻合较好,验证了数值模拟方法的可靠性。
(2) 吸气源的布置及吸气气流速率的大小均会影响对涡激振动的抑制效果。当吸气气流速率取值恰当时,采用上游幅上表面迎风侧栏杆基石处、下游幅上表面背风侧栏杆基石处、上游幅和下游福箱梁底部左右两侧开孔的控制措施能较好地抑制双幅主梁的涡激振动。
(3) 主动吸气控制措施使得双幅主梁受到的升力对结构做功显著减小甚至做负功,从而有效地抑制了主梁的涡激振动响应。
(4) 主动吸气控制措施通过对流场注入外部能量,抑制了涡的发展和运动,使绕流场得到修正。吸气气流与回流相互作用,从而抑制了主梁的涡激振动。

