喷管非轴对称性对超声速欠膨胀射流激波啸叫影响实验研究

张俊龙, 梁 勇, 覃 晨

(中国空气动力研究与发展中心 低速空气动力研究所,四川 绵阳 621000)

超声速射流在高压管路排气、军用飞行器推进系统、火箭推进系统中广泛存在。非理想膨胀的超声速射流,会产生非常强烈的激波啸叫噪声(screech tone),严重时会引起喷管疲劳,引发安全风险。早在20世纪50年代,Powell[1]针对超声速射流的激波啸叫噪声开展了系列研究。实验发现轴对称射流激波啸叫噪声的频率随射流马赫数的变化并非是单调的,而是存在阶跃现象(distinct jumps)。他根据频率特性的不同将轴对称超声速射流的激波啸叫噪声分为4个不同的啸叫级(screech stage),分别以A、B、C、D命名。对于较低完全膨胀马赫数(Mj<1.4),圆形超声速射流通常仅处于A模态和B模态。A模态又可分为A1模态和A2模态。Davies等[2-3]在射流两边布置传声器,并对测得的噪声信号进行相关分析,发现不同啸叫级对应不同的模态(mode),其中A为轴对称模态(axisymmetric),B为弯曲模态(sinuous),C为螺旋模态(helical),D较为少见。因此业界也将超声速射流的啸叫级称为啸叫模态(screech modes)。此后很多研究人员针对轴对称超声速射流的激波啸叫模态开展了大量研究,如发展了频率预测公式[4-6],确定了模态的稳定性特征[7],对模态的噪声机理进行深入研究[8-9]等。但是目前为止,大多研究都是针对激波啸叫频率及模态特性进行的。由于激波啸叫噪声声压级对来流条件、唇口厚度等具有较强的敏感性,不同的试验条件测量的结果一致性较差,因而,对于激波啸叫噪声声压级的研究较少。此外,对于不同啸叫模态下,噪声辐射特性的差异以及对模态阶跃的合理解释目前研究仍较缺乏。

喷口外形是影响超声速射流激波啸叫模态特性的重要因素之一[10]。研究不同喷口外形的激波啸叫噪声特性能为激波啸叫噪声模态及模态阶跃机理研究提供新的支撑。目前国际上非轴对称超声速射流激波啸叫的研究大多针对矩形射流展开。Raman等[11]研究发现,随射流马赫数的增加,矩形射流不存在模态切换,在马赫数范围1.1～1.6,激波啸叫基频和矩形射流流场均表现为反对称模态,即沿着短轴上下摆动模态(flapping)。激波啸叫二阶频率表现为对称模态。而Gutmark等[12]发现,在较低马赫数时,矩形射流也存在轴对称模态。Kaji等[13-15]表明,矩形较低马赫数时,矩形超声速射流同时存在轴对称和反对称模态。显然,矩形超声速射流表现出的摆动模态与矩形喷口结构相关,矩形喷口的非轴对称性抑制了弯曲和螺旋模态的运动。如果喷口外形为其它形状时,如三角形喷口,其独特的喷口外形是否会对矩形喷口的摆动模态产生抑制,进而抑制整个超声速射流的激波啸叫噪声辐射?遗憾的是对于圆形和矩形喷口以为的其它外形的喷口研究很少有文献提及。

本文将着重研究对比圆形、正方形以及正三角形收缩喷管的超声速射流噪声激波啸叫的辐射特性及模态特征,为激波啸叫噪声的抑制提供另一种思路。为确保不同喷口外形实验结果的可对比性,本研究加工的圆形、正方形和正三角形的收缩喷管具有相同的出口面积、唇口厚度和收缩比(收缩比12.57)以及相似的收缩曲线。实验研究在校准级消声室内的射流模拟装置上展开。通过实验研究发现,超声速射流激波啸叫噪声的辐射特征和模态特性确实与喷口外形密切相关,不同外形的喷口表现出完全不同的模态特性,而不同模态特性对应的激波啸叫噪声声压级分布也存在较大差异。

1 装置及测量方法

1.1 射流模拟装置和实验喷口

本研究所采用的消声室内的射流模拟装置照片如图1所示。该射流模拟装置建立在全消声室内。消声室净空间尺寸为10.8 m(长)×8.4 m(宽)×7.0 m(高),消声室截止频率100 Hz。消声室满足ISO-3745标准,本底噪声仅7 dB(A)。射流模拟的动力来源于CARDC的2 MPa、20 000立方中压气源,通过两级调压控制系统对目标压力进行控制。系统压力控制精度0.1%,最大供气质量流量为2 kg/s,核心区射流速度最大可达1.7 Ma[16]。

图1 CARDC射流模拟装置噪声实验照片Fig.1 Photo of jet simulator noise test at CARDC

为进行不同喷口出口截面形状的射流激波啸叫噪声研究,加工了由圆形过渡到目标外形的收缩段和喷口。实验喷口出口截面形状分别为圆形、正方形和正三角形。所有喷口的出口截面积均为25 cm2,唇口厚度0.8 cm。收缩段上游通过内径20 cm圆形法兰与射流模拟装置稳定段连接。三种喷口的收缩段长均为20 cm,收缩比为12.57。收缩段下游为5 cm的等直段喷口。

1.2 实验测量及数据处理方法

为测量超声速射流激波啸叫噪声远场辐射特性,本实验在与射流轴线同高的平面,以射流喷口出口中心为原点,半径4m处布置三个远场传声器测点,极角(射流出口截面中心与传声器的连线与射流轴线下游方向的夹角)分别为30°、90°和120°,分别测量射流激波啸叫向上游、侧边和下游方向的噪声辐射。为获得超声速射流激波啸叫噪声的模态特性,在喷口出口截面上周向等间隔布置了12个传声器。该传声器阵列通过安装座连接在收缩段上游法兰上,如图1所示。周向阵列测量的平面位于喷口出口平面下游10.8 cm(2倍喷口水力直径),相邻传声器周向角度间隔30°,传声器头部距离喷口轴线15 cm。

所用传声器型号为G.R.A.S.公司的1/4英寸自由场传声器46BE,前置放大器为G.R.A.S. 26CB。传声器及放大器的分析频率范围为:4 Hz～100 kHz;动态范围:35 dB(A)～160 dB;灵敏度:4 mV/Pa。数据采集系统采用BBM-PAK噪声振动测试分析系统。实验采样时间设为30 s,采样频率204.8 kHz。数据频谱分析采用Welch求功率谱的方法进行,每个数据块长度为16 834个数据/块,分析的窄带信号频率间隔为12.5 Hz。

2 实验结果的机理分析

2.1 超声速射流远场噪声频谱

图2为射流完全膨胀马赫数Mj=1.34,极角分别为120°(上游方向)、90°(侧边方向)和30°(下游方向)时,相同状态不同次实验测得的超声速射流噪声重复性结果。由结果可知,由于研制的射流模拟装置具有较高的压力控制精度,不同次实验获得的噪声测量结果重复性很好,测得的啸叫峰值声压级波动在1 dB以内。

(a) 极角120°

(b) 极角90°

(c) 极角30°图2 典型工况下超声速射流噪声频谱重复性结果,Mj=1.34Fig.2 Repeatablity results of supersonic jet noise spectral under typical condition,Mj=1.34

由图2可知,下游方向低频的湍流混合噪声要明显大于侧边方向和上游方向。激波啸叫噪声的基频(2 225 Hz)声压峰值随极角的变化不大,声压级差量在5 dB以内。倍频(4 450 Hz)声压峰值在极角90°方向要明显大于上游方向和下游方向,不同极角位置之间声压级的差量超过10 dB。

图3给出了圆形、正方形、正三角形喷口在射流完全膨胀马赫数Mj=1.34,极角分别为120°、90°和30°时的频谱结果。由结果可知,圆形喷口与正方形喷口的激波啸叫频率和幅值均较为接近,而三角形喷口激波啸叫噪声差异较大。圆形喷口激波啸叫基频频率(2 225 Hz)附近,三角形喷口的激波啸叫噪声声压较低,但三角形喷口存在额外的啸叫频率(3 062 Hz)。该现象还将在后文中作进一步分析。

(a) 极角120°

(b) 极角90°

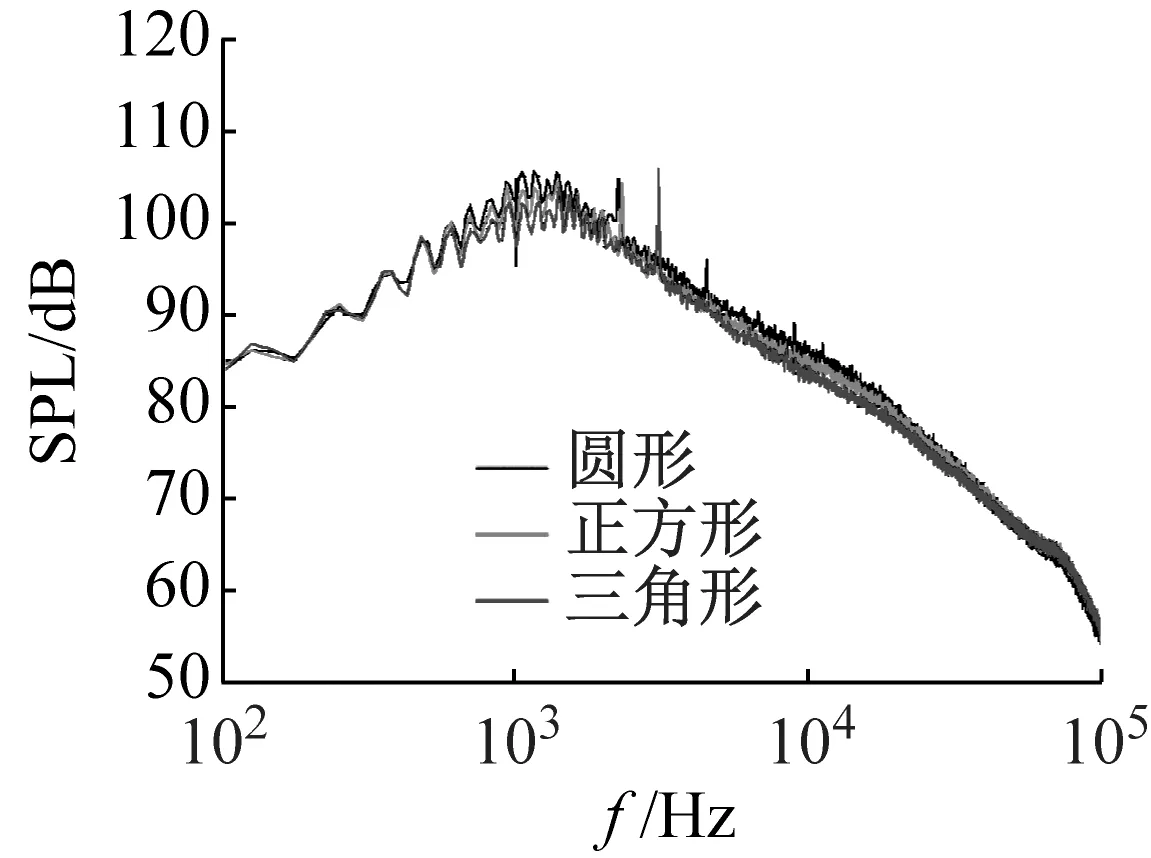
(c) 极角30°图3 不同喷口外形超声速射流噪声频谱对比,Mj=1.34Fig.3 Spectral comparison of supersonic jet noise with different nozzle shapes,Mj=1.34

2.2 超声速射流激波啸叫频率和幅值特性

图4给出了不同外形喷口超声速射流激波啸叫频率随射流完全膨胀马赫数Mj的变化结果。由结果可知,随射流完全膨胀马赫数的增加,圆形喷口和正方形喷口激波啸叫频率逐渐由A1模态过渡到A2模态,然后过渡到B模态。正三角形喷口在完全膨胀马赫数较低时没有出现激波啸叫噪声,不存在A1模态;在完全膨胀马赫数较高时,激波啸叫为B模态,还出现了额外的频率较高的模态,本文将其命名为E模态。该啸叫频率也可从图3的频谱结果中观察到。

图4 不同外形喷口激波啸叫频率随射流完全膨胀马赫数的变化Fig.4 Frequency of screech tone versus fully expanded jet Mach number for jets with different nozzle shapes

由图4可知,对于圆形喷口,A2模态出现的马赫数范围较窄,Mj不到1.20时便过渡到了B模态,而正方形喷口直到Mj=1.26才过渡到B模态。三角形喷口Mj在1.20～1.23之间都存在A2模态和B模态共存的现象,在Mj=1.32～1.37范围内存在B模态和E模态共存的现象。

不同的超声速射流的激波啸叫模态,除对应的频率特性不同外,其幅值特性也存在较大差异。由于激波啸叫声压级对来流条件、唇口厚度等具有较强的敏感性,不同试验条件测量的结果一致性较差,因而,较难获得可信的规律性结果。本期实验为获得喷口外形对超声速射流激波啸叫声压级的影响规律,实验工况除喷口外形外,尽量保持其它参数,如面积、唇口厚度、来流条件等的高度一致,加上实验结果较好的重复性,因此所得的结果可用于激波啸叫幅值特性的分析研究。图5给出了90°极角方向不同模态下的圆形超声速射流激波啸叫基频和倍频的幅值随射流完全膨胀马赫数的变化情况。对于A1和A2模态,随射流完全膨胀马赫数的增加,激波啸叫基频的幅值增加,达到最大值后,随完全膨胀马赫数的增加,激波啸叫基频幅值开始减小,直至发生激波啸叫模态的阶跃。在B模态时,激波啸叫基频幅值随射流完全膨胀马赫数的增加而振荡变化,但没有明显的增加趋势。而对于激波啸叫倍频,相比A模态,圆形射流B模态的激波啸叫倍频幅值明显增加,其幅值增量达13 dB以上,且随射流完全膨胀马赫数的增加,B模态激波啸叫倍频幅值出现波动性的增长。

(a) 激波啸叫基频

(b) 激波啸叫倍频图5 圆形超声速射流激波啸叫幅值,极角90°Fig.5 Amplitude of screech tone of circular supersonic jet at 90° polar angle

实验发现,相对圆形喷口和正方形喷口,在较低马赫数条件下,正三角形喷口能够极大抑制超声速射流的激波啸叫噪声,结果如图6所示。圆形射流和正方形射流在射流完全膨胀马赫数1.09时便出现了明显的激波啸叫噪声,而三角形射流的激波啸叫噪声直至马赫数1.19以后才出现,且在A模态下其幅值明显小于圆形射流和正方形射流。

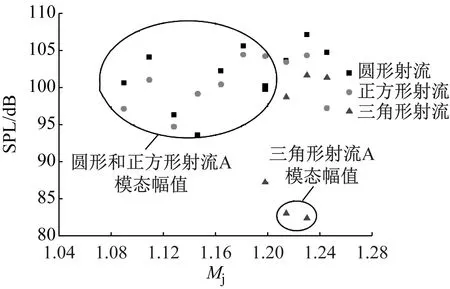
图6 不同形状喷口超声速射流激波啸叫幅值对比,极角90°Fig.6 Amplitudes of screech tone of supersonic jets with different nozzle shapes at 90° polar angle

由于B模态啸叫基频和倍频相比A模态具有较高的啸叫幅值。本研究针对不同喷口外形的B模态激波啸叫基频和倍频的幅值进行了对比研究,其结果如图7所示。

(a) 激波啸叫基频

(b) 激波啸叫倍频图7 不同形状喷口超声速射流激波啸叫B模态幅值对比Fig.7 Amplitudes of screech tone of supersonic jets with different nozzle shapes at B modes.

由图7可知,圆形射流和正方形射流的激波啸叫B模态基频幅值相当,而三角形射流激波啸叫B模态基频幅值要明显偏小。在Mj=1.32以上时,随着射流完全膨胀马赫数的增加,三角形射流激波啸叫B模态基频幅值开始明显减小,同时出现了较高啸叫幅值的E模态。相同马赫数条件下,三角形射流激波啸叫E模态基频幅值要略大于圆形射流和正方形射流的激波啸叫B模态幅值。对于圆形射流和正方形射流,极角90°位置,出现了要明显大于激波啸叫基频幅值的激波啸叫倍频噪声。其中正方形射流的激波啸叫倍频幅值要略小于圆形射流,而三角形射流激波啸叫倍频幅值要明显小于圆形射流和正方形射流。在Mj=1.32以上时,三角形射流激波啸叫出现了E模态,然而无论是B模态还是E模态的倍频噪声,其幅值均都要明显小于圆形或正方形射流,差异达16 dB以上。

整体而言,相比圆形射流,正方形射流激波啸叫噪声幅值略有减小,而三角形的喷口外形对超声速射流激波啸叫具有明显的抑制作用,其对激波啸叫的抑制机理值得进一步研究。

2.3 超声速射流激波啸叫周向方位角模态特性分析

超声速射流激波啸叫的频率与幅值特性与激波啸叫噪声的周向模态特性密切相关。为研究不同工况下,超声速射流噪声的周向模态特性,本研究在喷口出口附近周向均匀布置了12个传声器组成的阵列(图1),用于超声速射流激波啸叫的周向模态分析。

超声速射流激波啸叫模态特性分析采用周向方位角重构(azimuthal decomposition)的方法进行。该方法被Cavalieri等[17]用于亚声速射流波包结构的周向模态分析,本文将该方法扩展至超声速射流激波啸叫的周向模态特性分析中。该方法如下:

将特定周向方位角Φ处的声压信号用周向模态傅里叶级数表达如下

(1)

式中:p(Φ,t)为周向方位角Φ处的声压时域信号;p(m,t)为m阶周向方位角模态下的时域信号。

其中p(m,t)为p(Φ,t)的傅里叶级数系数,其表达式如下

(2)

式中:p(Φk,t)为第k个传声器,周向方位角为Φk的传声器测得的声压时域信号;n为传声器数量,本实验中为12个。

由于声压信号为实数,p(m,t)具有如下特征

p(-m,t)=p*(m,t)

(3)

将周向模态时域信号定义为

p0(t)=p(m=0,t)

pm(t)=p(m,t)+p(-m,t), ifm≠0

(4)

此时,周向模态时域信号均为实数。对于射流噪声,前几阶周向模态能量占比最大,因此通常只分析前几阶的周向模态。m=0阶的周向模态为轴对称模态,通常认为与轴向的非紧致声源即波包结构密切相关;m=1阶模态为螺旋模态,m=2阶模态为双螺旋模态,它们的能量与湍流尺度能量相关。0阶和1阶模态形式如图8所示。

(a)

(b)图8 射流噪声0阶和1阶周向模态[18]Fig.8 Azimuthal modes m=0 and m=1 of jet noise

将周向模态时域信号进行基于时间的频域变换,即可得到不同周向方位角模态下的频谱结果。通过分析啸叫频率点下不同方位角模态(通常只考虑前三阶方位角模态,即m=0、1、2)的声压能量占比即可获得该啸叫频率点占主导地位的周向方位角模态特性。实验获得的圆形超声速射流在Mj=1.11时,前三阶周向方位角模态频谱和总声压级频谱如图9所示。由结果可知,目标工况超声速射流噪声低频段,m=0阶的轴对称模态占主导,其噪声主要是由非紧致的大尺度旋涡结构产生,高频段射流噪声由m=1和m=2阶螺旋模态占主导,其噪声主要是小尺度湍流混合噪声引起。在啸叫频率点上,可以发现,该处总声压级与m=0阶模态的声压级相当,即Mj=1.11时,圆形超声速射流的啸叫模态主要为m=0阶的轴对称模态。

图9 圆形射流激波啸叫周向方位角模态频谱,Mj=1.11Fig.9 Spectral of individual modes for circular jet,Mj=1.11

为方便分析不同工况下的激波啸叫周向模态特性,本文基于图4的不同外形喷口啸叫模态随马赫数分布结果,针对典型的A1模态、A2模态、B模态及三角形射流的E模态啸叫频率,选定特定的射流完全膨胀马赫数,以开展周向方位角模态的实验分析。本研究选定的射流完全膨胀马赫数Mj分别为1.11、1.20和1.34,该马赫数囊括了圆形射流和正方形射流激波啸叫的A1、A2和B模态以及三角形射流的A2、B和E模态。在选定工况下,对如图1所示的周向分布的传声器测量结果,应用周向方位角重构的方法,获得了不同类型激波啸叫周向方位角模态特性。具体结果如表1、表2所示。

表1 不同激波啸叫模态基频下的周向方位角模态声压级Tab.1 Sound pressure level of different azimuthal modes under fundamental frequency of screech tone modes

表2 不同激波啸叫模态倍频下的周向方位角模态声压级Tab.2 Sound pressure level of different azimuthal modes under second harmonics of screech tone modes

由表1和2结果可知,对于超声速射流激波啸叫基频,无论圆形、正方形还是三角形射流,其A1、A2模态均由m=0阶能量占主导,B模态由m=1阶能量占主导。由此可知,A1,A2模态基频是轴对称模态,而B模态基频是螺旋模态,这与文献[3]得到的圆形超声速射流模态结果一致。该结果也说明了本文图4所采用的归类命名方法是可行的,分类符合各自的模态特性。由结果还可知,文献[11]给出了矩形射流的摆动模态并未出现在正方形射流中。对于正三角形超声速射流出现的特有的激波啸叫E模态,其基频由m=0阶能量占主导,表明其为轴对称模态。对于超声速射流激波啸叫倍频,圆形射流A1模态同时存在轴对称模态和螺旋模态,圆形射流A2模态为二阶螺旋模态,而正方形射流A1、A2模态均为轴对称模态,三角形射流A2模态的倍频较弱,没有被观测到。圆形射流、正方形射流和三角形射流的B模态倍频均为轴对称模态。三角形E模态的倍频也为轴对称模态。

综上可知,喷管的非轴对称性对同轴模态影响较小,但是对螺旋模态具有明显的抑制作用。相比圆形射流,正方形射流达到B模态所需的射流完全膨胀马赫数更大,而三角形射流B模态啸叫的声压级明显要低于圆形射流和正方形射流,而且在完全膨胀马赫数大于1.32时,出现了同轴模态特性的E模态。

3 结 论

本文针对圆形、正方形和正三角形喷口开展了超声速射流激波啸叫频率,幅值和模态特性的实验研究。主要结论如下:

(1) 相比圆形射流,正方形射流激波啸叫噪声幅值略有减小,而三角形的喷口外形对超声速射流激波啸叫具有明显的抑制作用。

(2) 圆形射流、正方形射流和正三角形射流激波啸叫A模态基频均为轴对称模态,B模态基频均为螺旋模态;圆形射流激波啸叫的倍频同时存在轴对称和螺旋模态,而正方形和三角形射流激波啸叫倍频仅存在轴对称模态。

(3) 在Mj=1.32以上时,随着射流完全膨胀马赫数的增加,三角形超声速射流出现了特有的E模态激波啸叫,其基频和倍频均为轴对称模态。

(4) 喷管的非轴对称性对同轴模态影响较小,但是对螺旋模态具有明显的抑制作用。