空间机械臂碰撞过程的模糊无模型自适应振动控制
浦玉学, 周润闰, 陈 演, 张 方
(1.合肥工业大学 土木与水利工程学院,合肥 230009; 2.复旦大学 航空航天系,上海 200433;3.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016)
近些年来,空间机械臂代替宇航员执行辅助对接、目标搬运、在轨建设以及捕获释放等空间操作任务成为重要发展趋势[1-2]。然而在空间机械臂执行上述任务[3]时,尤其是在对接、捕获过程中不可避免地与合作目标或非合作目标发生碰撞[4]。无论主动捕获或被动碰撞均会引起机械臂瞬时动量急剧变化,机械臂杆弹性振动加剧,轨迹跟踪精度降低,甚至会导致空间机械臂系统失稳[5]。
空间机械臂碰撞过程的研究受到了广泛关注。Wee等[6]针对完全刚性臂建立了空间机器人的动力学模型,基于最小碰撞冲击的目标,研究空间机器人的轨迹优化算法。Yoshikawa等[7]将空间机械臂与目标碰撞物混合体等价为一个弹簧阻尼系统,进一步分析在碰撞过程中系统对于碰撞力的响应。董楸煌等[8]对漂浮基空间机械臂捕获目标卫星过程及捕获后混合体系统响应进行动力学和控制分析。贾庆轩等[9]对空间机械臂在轨捕获问题进行了碰撞分析,分析表明空间机械臂在碰撞过程中存在碰撞力矩可能超过电机承受力矩的问题。
目前关于空间机械臂碰撞过程研究主要以合作目标(卫星捕获)为研究对象,但对于非合作碰撞物(如太空碎片)与空间机械臂产生碰撞的研究较少。王文龙等[10]对航天器对接、捕获技术进行综述,提炼了捕获非合作目标的八项关键技术,给出在该领域开展研究的方向和建议。郭吉丰等[11]探讨了空间非合作目标柔性捕获机构的研究进展,提出一步式消旋法更具有研究前景。然而随着太空环境逐渐恶化,非合作碰撞物对空间机械臂的干扰不容忽视,尤其是碰撞引起的机械臂系统模型突变,导致空间机械臂的运动状态与系统参数急剧变化且不可预测,给传统基于精确模型参数的控制方法带来严重挑战。另外,空间机械臂的轻量化设计趋势使得机械臂杆柔性变大,上述碰撞将引起机械臂杆产生较大的弹性振动[12],严重影响机械臂轨迹跟踪和末端定位精度。由于非合作碰撞物的不确定性,如何采用非模型控制方法实现空间机械臂碰撞过程的轨迹跟踪和振动控制逐渐成为研究热点。
无模型自适应控制(model-free adaptive control, MFAC)指仅利用受控系统的输入、输出数据直接进行控制器的设计和分析,并能实现未知非线性受控系统的参数自适应控制和结构自适应控制的一种控制理论与方法。MFAC算法具有算法简单,计算量小的优点,但对于步长因子和权重因子的取值较为敏感。对于空间机械臂碰撞过程的模型参数和振动响应急剧变化的情况,传统无模型控制算法难以达到较优的控制效果,因此设计合适的控制参数的在线自整定策略至关重要。
考虑到空间柔性机械臂碰撞过程模型参数的不确定性,本文建立空间机械臂与非合作碰撞物的碰撞过程动力学模型,并以此为控制对象。提出了模糊策略与无模型自适应控制相结合的模糊-无模型自适应控制(Fuzzy-MFAC)方法,对MFAC算法中步长因子与权重因子进行在线自整定,提高无模型自适应控制性能。
1 空间机械臂动力学模型
将空间机械臂作为研究对象,分别采用拉格朗日方程和牛顿-欧拉法建立空间机械臂和非合作碰撞物的动力学模型,然后基于动量守恒原理对两者碰撞过程进行分析,根据其相互作用内力关系,联立两者的动力学方程,得到机械臂-碰撞物混合系统综合动力学模型。本章建立碰撞过程的空间机械臂动力学模型,为后文控制方法验证和控制仿真试验开展提供模型对象。
1.1 空间机械臂与碰撞物动力学模型
空间机械臂在轨运行与非合作碰撞物发生碰撞的运动过程,如图1所示。碰撞模型由卫星主体、空间机械臂与非合作碰撞物组成。
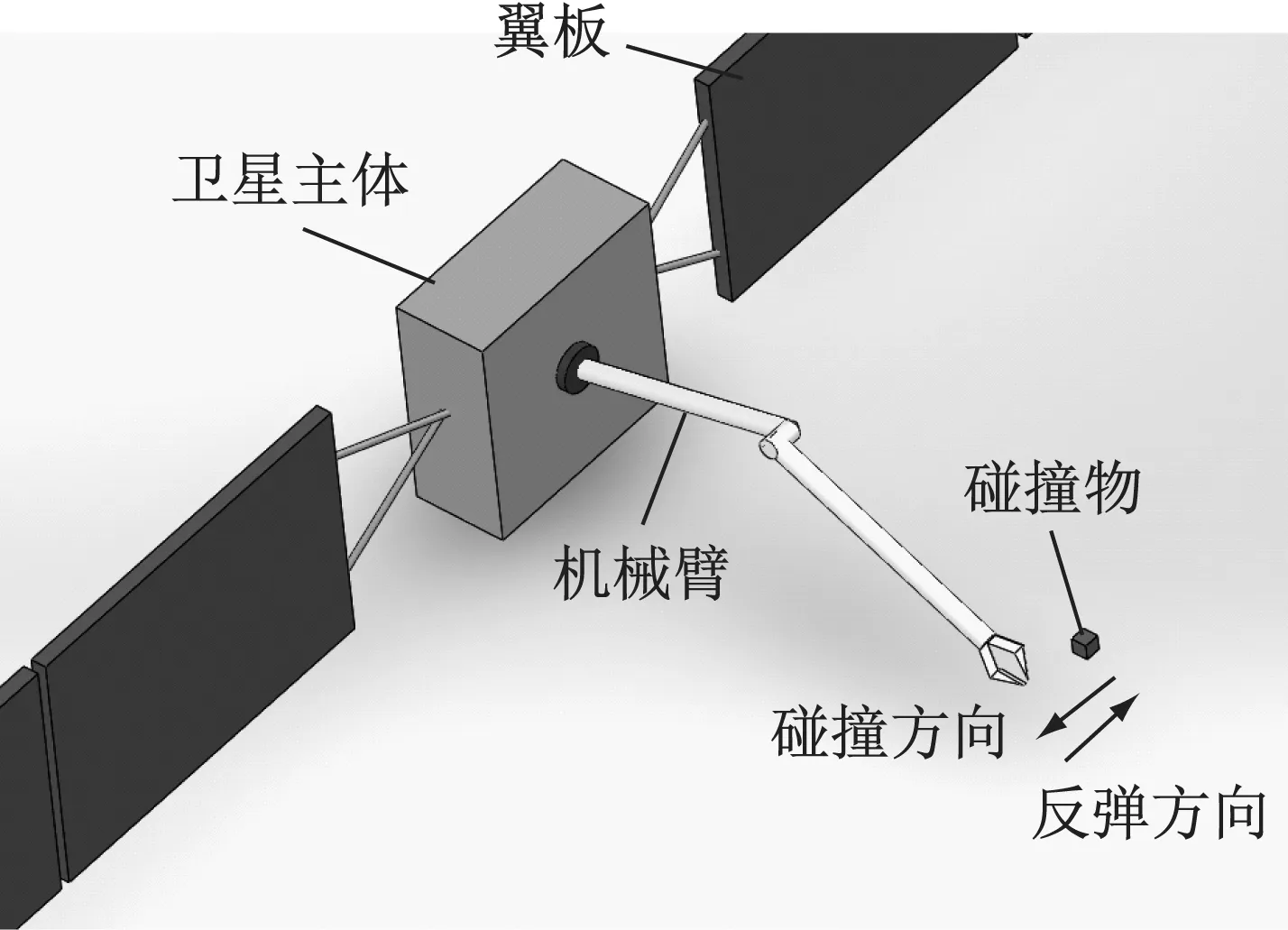
图1 空间机械臂碰撞过程Fig.1 Collision process of space manipulator
为了简化模型,将空间机械臂与卫星主体相连的臂杆视为刚性臂,着重讨论第二根柔性臂杆,并假设关节角转动和弹性振动与非合作碰撞物的运动均发生在同一个平面上。建立坐标系,如图2所示。OX0Y0为固定于关节转轴上的惯性坐标系,OX1Y1为机械臂发生弹性振动时的参考坐标系,始终与柔性机械臂的根部相切。m1,l1,ρ1,E1,I1,A1分别为柔性臂的质量、长度、密度、弹性模量、对中性轴的惯性矩、横截面积。τ为关节的驱动力矩,θ为柔性臂转动角位移,ω(x,t)为柔性臂的弹性位移,J1为关节的转动惯量。m2和J2分别为非合作碰撞物的质量和中心转动惯量。
1.1.1 柔性机械臂模型
本文假设机械臂为均匀细长杆,等效为Euler-Bernoulli梁[13],在t时刻杆上任意一点P的横向弹性变形可由假设模态法表示为
(1)
式中:qi(t)与Φi(x)分别为机械臂的第i阶模态坐标和模态函数;n为保留的模态项数,此处取n=4。则P点相对于参考坐标系OX1Y1的矢量rp为
rp=x1eX1+ω(x1,t)eY1
(2)
同时eX1与eY1在惯性坐标系OX0Y0下可以写为
(3)
均对t求导可得
(4)
(6)
机械臂的系统弹性势能可以表示为
(7)
由于碰撞前机械臂系统与碰撞物之间无相互作用,则根据第二类拉格朗日方程可得柔性机械臂系统的动力学方程为
(8)
式中:M∈5×5为柔性机械臂系统的广义质量矩阵;H∈5×1为包含科氏力和离心力矢量;K∈5×5为系统刚度矩阵;τ为关节对柔性机械臂的作用力矩。
1.1.2 非合作碰撞物模型
对于非合作碰撞物的刚体系统,可得非合作碰撞物的速度与对应广义坐标速度的运动学关系为
(9)
式中:vt为非合作碰撞物在惯性坐标系下的线速度;α为非合作碰撞物质心在惯性坐标系下坐标以及姿态角,α=(xt,yt,θt)T;Jt∈2×3为碰撞物的运动Jacobian矩阵。使用拉格朗日方程建立动力学方程为
(10)
式中:Mt∈5×5为非合作碰撞物系统的广义质量矩阵;Ct∈5×1包含科氏力和离心力矢量。
1.2 碰撞过程机械臂系统动力学分析
在碰撞的瞬时,机械臂与碰撞物同时受到冲击力作用,则两个动力学方程改变为
(11)
(12)
式中:Fp为机械臂末端所受到的冲击力;Fp′为刚体系统所受外力。由牛顿第三定律可知,
Fp=-Fp′
(13)
则有
(14)
(15)
由于碰撞过程非常短暂,则Δt趋向于0,又碰撞力极大。做出假设,碰撞过程中系统广义坐标并未发生明显变化而广义速度瞬时发生了变化,柔性臂系统与碰撞物系统的广义质量矩阵、Jacobian矩阵均为广义坐标的函数,则视为未发生明显变化,令关节对柔性机械臂的作用力τ=0,再进一步积分可得
(16)
式中,左侧为有限量,右侧因为Δt趋向于0,则积分总和趋向于0,则式(16)可改写为
(17)
非合作碰撞物与机械臂碰撞后的工况分为两种情况:机械臂与非合作碰撞物碰撞后吸附;机械臂与碰撞物碰撞后弹开。
1.2.1 空间机械臂与非合作碰撞物碰撞后吸附
由两者发生碰撞后发生吸附不再分开,则两个系统速度相同有
(18)
联立式(15)与(16)有
(19)
由此得到了碰撞过后系统的广义速度公式,这体现了碰撞过程中冲量对系统运动状态的影响,后文继续进行碰撞后的动力学分析。
碰撞过后空间机械臂与非合作碰撞物发生吸附,成为一个整体,因此放在一起进行动力学分析,联立两个单独系统的动力学方程
(21)
消去碰撞力Fp与Fp′,再由非合作碰撞物吸附在机械臂末端可整理得混合体系统动力学方程为
(22)
式中:Mz∈5×5为整体的广义质量矩阵;Hz∈5×1为交叉耦合矩阵;Kz∈5×5为刚度矩阵;G为作用力位置矩阵,G=(1,0,0,0,0)T。
1.2.2 空间机械臂与非合作碰撞物碰撞后弹开
空间机械臂与非合作碰撞物碰撞后弹开等同于机械臂在某一时刻受到一个瞬时碰撞产生外部冲击力F,冲击力矩为τa。令碰撞处产生一个虚位移δXa,机械臂的位置几何关系为
δXa=Jδq
(23)
根据虚功原理,机器人系统的主动力、主动力矩对作用点的虚位移做功之和为零,即
(24)
联立式(20)与(21)可得
τa=JTF
(25)
当机器人末端受到外部冲击作用时,根据静力平衡条件,机器人系统的碰撞动力学方程为
(26)
2 空间机械臂系统主动控制方法
目前,针对空间机械臂的控制方法大多为基于模型的控制[14],例如力矩补偿法、阻抗控制等[15],这些传统的控制方法需要得到系统精确的模型[16-17],而对于发生碰撞的机械臂系统而言获取精确的模型参数很难实现。无模型自适应控制因其基于系统输入、输出数据进行控制器的设计特点,能够适应于空间机械臂在太空工作时发生碰撞导致模型参数难以精确描述的情况,由此得到不依赖于柔性机械臂精确参数的MFAC算法是必要的[18]。
2.1 无模型自适应控制
MFAC算法是一种无需建立过程模型的自适应控制方法,即控制系统不考虑模型,也无需精确的碰撞过程定量知识。MFAC算法的优势在于只需要系统的输入量与输出量就可以对控制对象进行有效控制,其控制原理如下
τ(k)=τ(k-1)+
(27)
式中:τ(k)为柔性机械臂的关节驱动力矩;ρ∈(0,1]是力矩步长因子,目的是使控制算法更具有一般性,λ>0是一个力矩权重因子,用来限制控制输入量的变化;y*(k+1)为期望柔性机械臂关节转动角速度;y(k)为实际的机械臂关节转动角速度。
对于非线性系统而言,关节转动角位移与关节驱动力矩之间必定存在一个非线性关系,令
(28)
则当Δτ≠0时,一定存在一个偏导数ψ(k),且该偏导数满足
Δy(k+1)=ψ(k)τ(k)
(29)
式中,ψ(k)的估计算法为
(30)
or |Δu(k-1)|≤ε
(31)

由伪偏导数方程和控制律方程可以得到无模型自适应控制器的设计不需要受控模型的具体参数,仅使用受控系统的I/O数据,其算法简单,计算量小的优点便于实现实时控制。但是由于MFAC算法对于步长因子和权重因子的取值较为敏感,不合适的初值会影响MFAC算法的控制性能。以空间机械臂为研究对象,使机械臂关节运动指令如下
(32)
式中:t0和tb为空间机械臂运动的起始时刻和终止时刻;θ0和θb分别为系统关节的起始位置和终止位置。设定θ0=0,θb=2π,运动时间tb=4 s,总仿真时间为10 s。无模型自适应控制参数ρ与μ对控制效果具有很大影响,为量化分析这种影响,控制器其他参数不变,取力矩步长因子ρ分别为0.1、0.2、0.3,混合体运动轨迹偏差如图3所示。控制器其他参数不变,取偏导数权重因子μ分别为0.2、0.4、0.6,混合体运动轨迹偏差如图4所示。

图3 ρ与运动轨迹偏差关系Fig.3 Relationship between ρ and trajectory deviation

图4 μ与运动轨迹偏差关系Fig.4 Relationship between μ and trajectory deviation
由此可以验证合适的初值能够提高MFAC算法的控制性能。由图3可得,随着ρ的增大,运动过程中跟随误差变大,末端振动变大,控制效果变差。由图4可得,随着μ的增大跟随效果更优,但是收敛速度变慢,整体控制效果变好。因此,在MFAC算法中实时更新其中的参数是必要的。
2.2 模糊-无模型自适应控制器设计
MFAC算法需要在控制过程中实时更新参数,而模糊策略能够根据系统的输入、输出误差在线调整控制系统的参数[19]。由此提出的模糊-无模型自适应控制(Fuzzy-MFAC)是在无模型自适应控制的基础上实时更新无模型自适应控制的参数,实现MFAC算法中的步长因子和权重因子进行实时在线整定。
模糊控制器的输入为[y*(k+1)-y(k)]与Δy(k),即期望柔性机械臂关节转动角位移对实际柔性机械臂关节转动角位移差值E;实际柔性机械臂关节转动角速度差值Ec。Δμ与Δρ为模糊控制器的输出,作为无模型控制器的输入对偏导数权重因子μ与力矩步长因子ρ进行修正,实现无模型控制器参数的实时整定[20]。基于Fuzzy-MAFC算法结构框图,如图5所示。

图5 模糊无模型控制器结构框图Fig.5 Fuzzy-MAFC controller block diagram
确定模糊化输入、输出变量及确定隶属度函数,则更新MFAC算法的参数为
(33)
式中:μ0与ρ0为柔性机械臂静止时设置的初值;μ与ρ为修正过后的MFAC算法参数;Δμ与Δρ为模糊控制器实时输出的参数变化量。
模糊控制器的精度由设计的论域数值决定,本文将根据空间机械臂的结构特点选择适应的模糊输入、输出论域。使模糊控制器输入变量的论域为[-0.6,-0.4,-0.2,0,0.2,0.4,0.6],输出变量的论域为[-0.3,-0.2,-0.1,0,0.1,0.2,0.3];模糊子集的设定为[NB,NM,NS,ZO,PS,PM,PB],分别为负大、负中、负小、零、正小、正中、正大。其隶属度函数如图6所示。
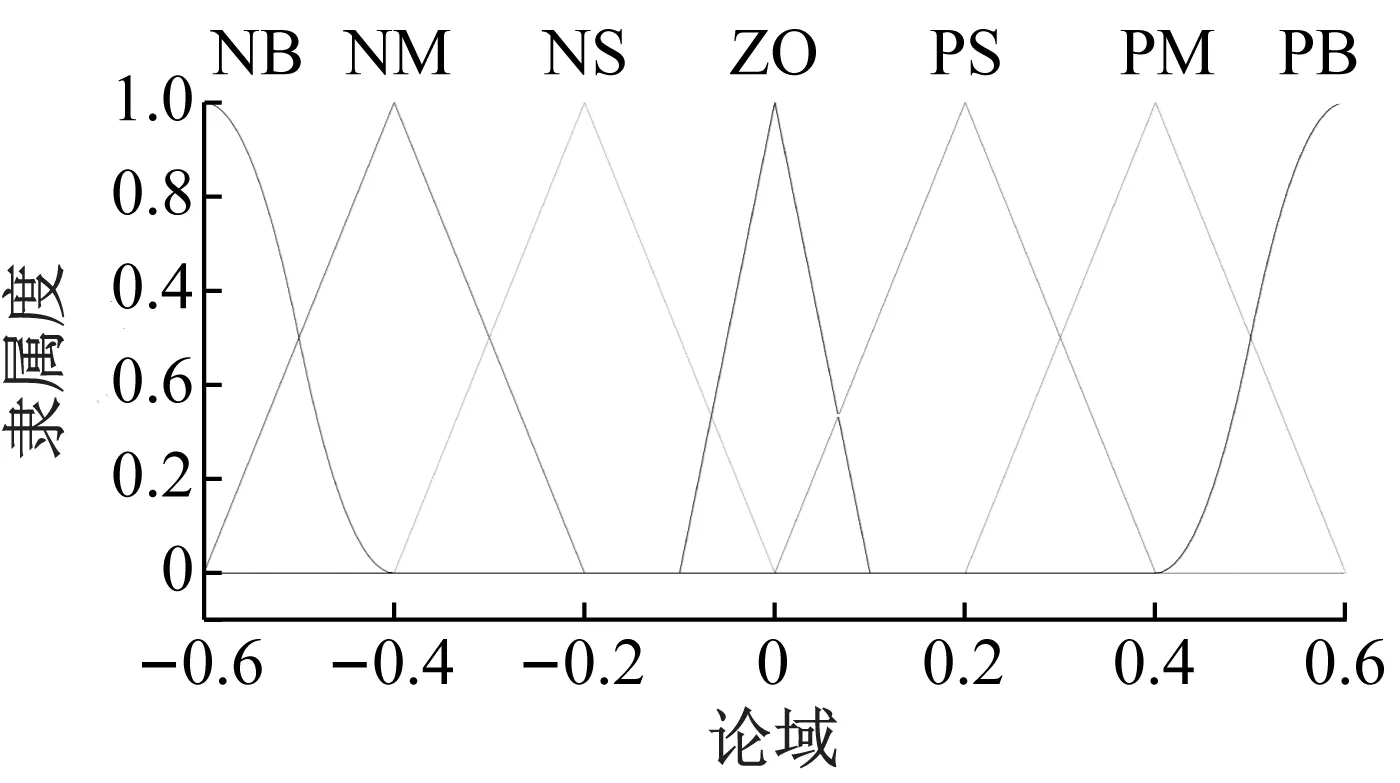
(a) E、Ec隶属度函数
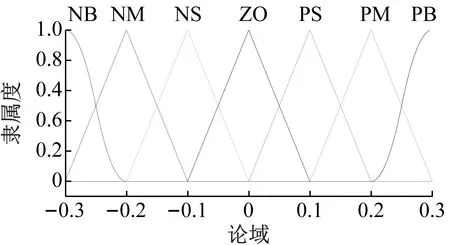
(b) Δμ、Δρ隶属度函数图6 输入输出变量隶属度函数Fig.6 Membership function of input and output variables
空间机械臂模糊控制规则具体为: 误差偏大时,需适当缩小误差,即E过大,则取较大Δμ与Δρ对误差进行调整;误差中等时,需适当缩小误差,并避免缩小时出现过度调整,以确保响应速度,即E中等,则缩小Δμ;误差偏小时,需保障稳定性,避免状态突变,即E过小,则取较小Δμ与Δρ对误差进行调整。由此得到Δμ与Δρ的模糊控制规则,如表1、表2所示。
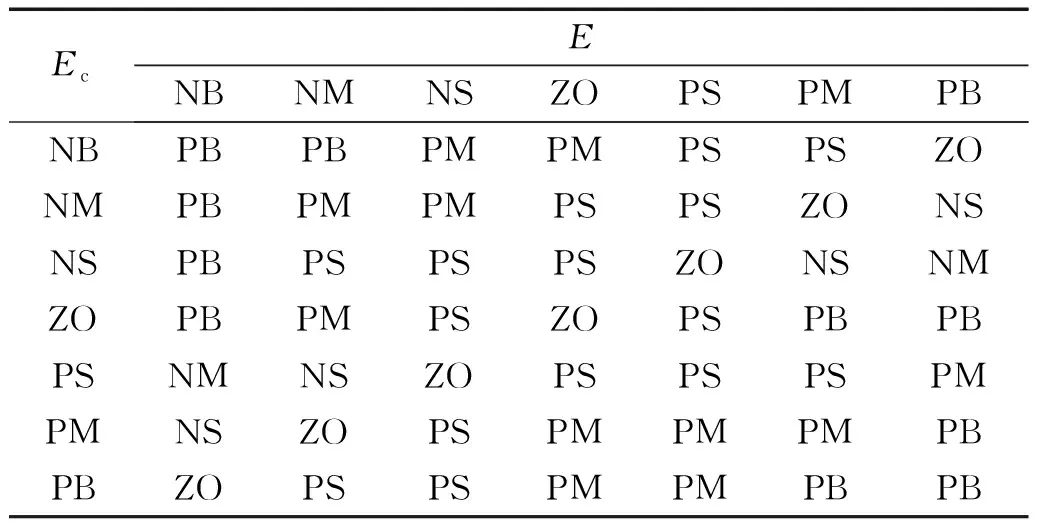
表1 Δμ的模糊控制规则表Tab.1 Fuzzy control rule table for Δμ

表2 Δρ的模糊控制规则表Tab.2 Fuzzy control rule table for Δρ
去模糊化即清晰化模糊推理所得理论[21],本文采用重心法进行解模糊,求解后得到输出变量Δμ与Δρ。
(34)
(35)
式中,μi与ρi为各组元素的权重。模糊控制器所得输出清晰量为Δμ与Δρ,再由式(33)可得对应的力矩步长因子ρ与偏导数权重因子μ。
3 数值分析仿真
对空间机械臂进行关于碰撞问题的仿真分析。将对同一被控对象在不进行任何控制(No Control)、仅使用传统MFAC算法和使用Fuzzy-MFAC方法三种状态进行仿真分析,揭示碰撞对于空间机械臂的影响,验证Fuzzy-MFAC方法的优越性。
仿真时设定空间机械臂与非合作碰撞物A、B的具体参数如表3所示。

表3 机械臂与碰撞物参数Tab.3 Manipulator and collider parameters
由机械臂参数可以分析得到机械臂第一阶频率为20.3 Hz。仿真过程中空间机械臂以式(36)所示轨迹进行运动
(36)
式中:t0和tb为空间机械臂运动的起始时刻和终止时刻;θ0和θb分别为系统关节的起始位置和终止位置。设定θ0=0,θb=π/2,运动时间tb=1 s,总仿真时间为10 s。
3.1 空间机械臂碰撞仿真试验设计
为讨论设计控制器对空间机械臂的控制效果,共设置三种空间机械臂与非合作碰撞物相碰撞的工况进行分析。在碰撞过程中碰撞物A会与机械臂碰撞后弹开,需较大的碰撞速度,设置为3 m/s,而碰撞物B在与机械臂发生碰撞后与机械臂发生吸附,碰撞速度较小,选取1 m/s的速度。
试验一:0~0.5 s空间机械臂正常工作,在0.5 s时,碰撞物A以3 m/s的速度与空间机械臂垂直碰撞,并与空间机械臂弹开,机械臂继续工作。
试验二:0~0.5 s空间机械臂正常工作,在0.5 s时,碰撞物B以1 m/s的速度与空间机械臂垂直碰撞,并与空间机械臂吸附,机械臂继续工作。
试验三:工况三设计为较为复杂的情况,整个运动过程空间机械臂共有三种状态。
阶段一:在0~0.5 s时,空间机械臂以式(31)所示轨迹进行正常工作。
阶段二:在0.5 s时,碰撞物A以3 m/s的速度与空间机械臂垂直碰撞,并与空间机械臂弹开,在0.5~2.0 s时,机械臂在受到碰撞后继续运动。
阶段三:在2.0 s时,碰撞物B以1 m/s的速度与空间机械臂末端垂直碰撞,吸附于空间机械臂末端。
3.2 碰撞仿真试验结果分析
试验一的仿真结果如图7所示。
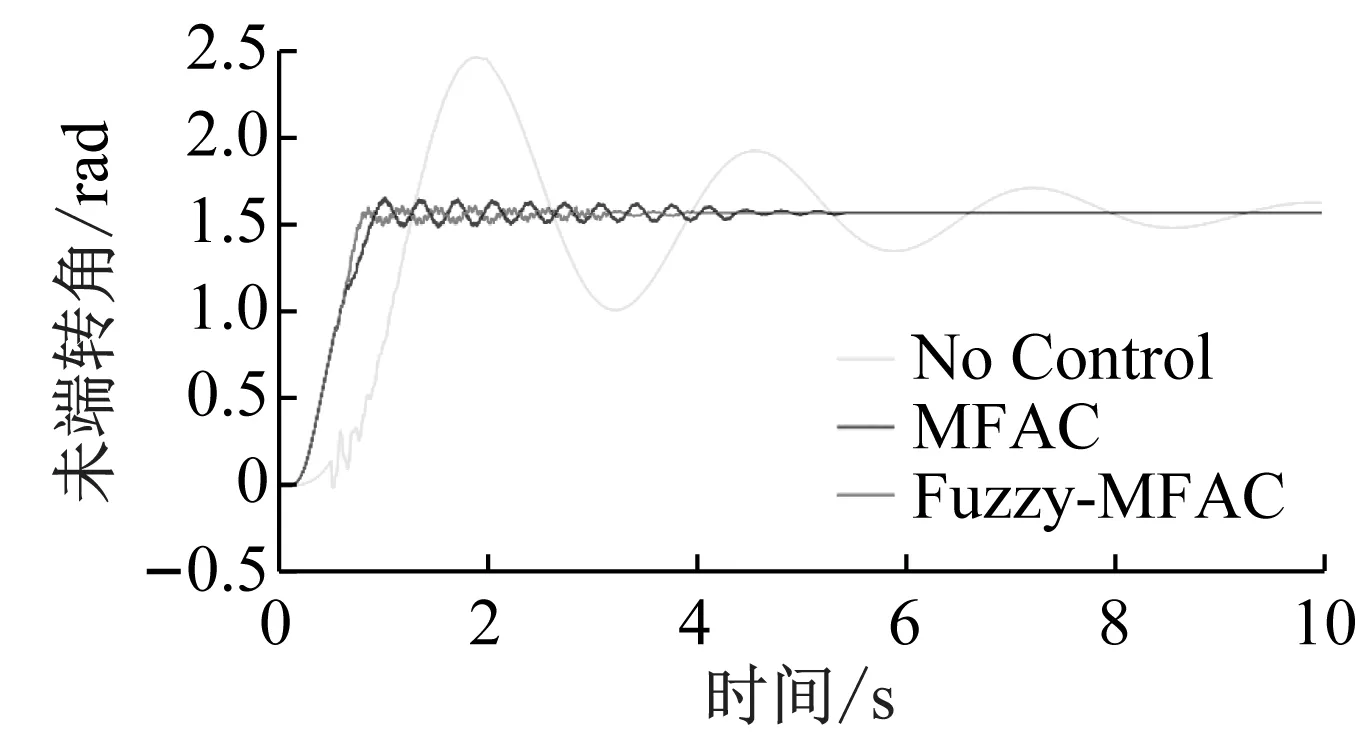
(a) 空间机械臂的末端转角响应
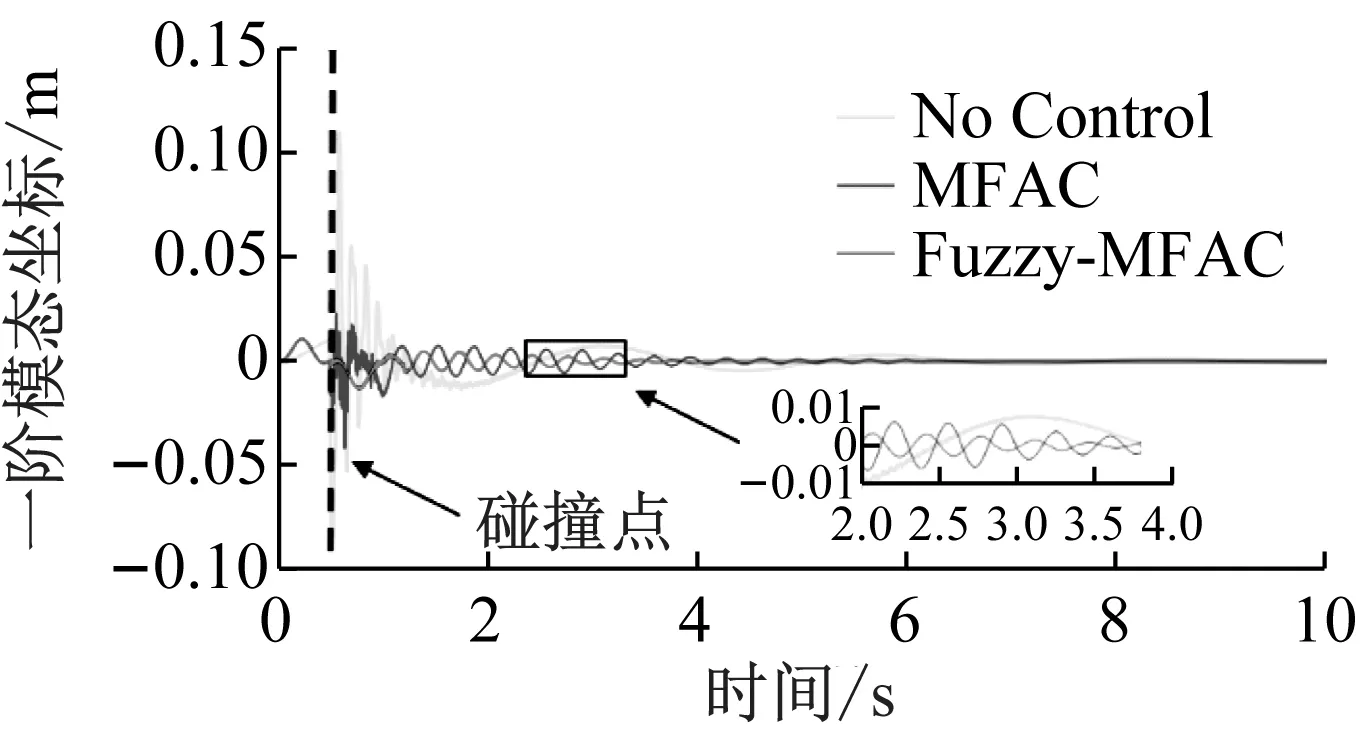
(b) 时域曲线

(c) 频域曲线


(d) 控制参数变化曲线图7 试验一仿真结果Fig.7 Simulation results of test one
由图7可知,空间机械臂与碰撞物的碰撞会严重影响空间机械臂的正常工作,在未控制情况下机械臂产生了往复运动,而Fuzzy-MFAC方法仿真振幅衰减小于90%的时间为4.2 s,传统MFAC算法仿真振幅衰减小于90%的时间为5.4 s,振动衰减速度提高了22%。对机械臂关节运动到位后的振动响应进行频域分析,结果见图6(c),可以发现Fuzzy-MFAC方法仿真结果相较于传统MFAC算法仿真结果在第一阶模态振动响应幅值降低了48%。
试验二的仿真结果如图8所示。

(a) 空间机械臂的末端转角响应

(b) 一阶模态变化时程

(c) 频域曲线

(d) 控制参数变化曲线图8 试验二仿真结果Fig.8 Simulation results of test two
由图8可知,MFAC算法对于模型的改变并不敏感,两种控制方法的控制效能均良好。Fuzzy-MFAC方法仿真结果相较于MFAC算法仿真结果振幅衰减的速率提高32%,第一阶频率降低了46%。碰撞物吸附在机械臂末端,可以从频响曲线上看出频率降低到18.1 Hz。
试验三的仿真结果如图9所示。Fuzzy-MFAC方法仿真振幅衰减小于90%的时间为4.8 s,而传统MFAC算法振幅衰减小于90%的时间为7.1 s,速率提高了34%,第一频率降低了42%。可以看出在复杂工况下,Fuzzy-MFAC方法的优点得到较好体现,跟随效果较优且稳定速度快。

(a) 空间机械臂的末端转角响应
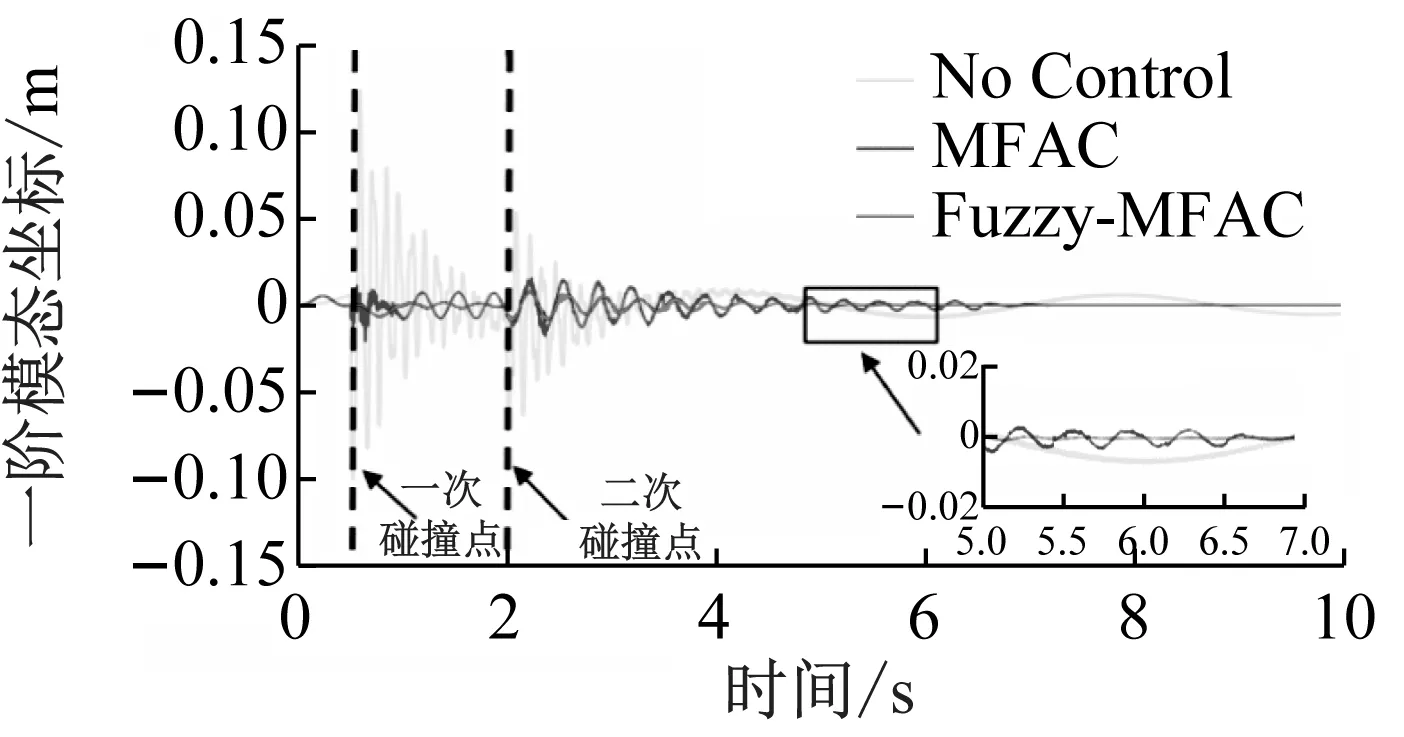
(b) 一阶模态变化时程与频域

(c) 频域

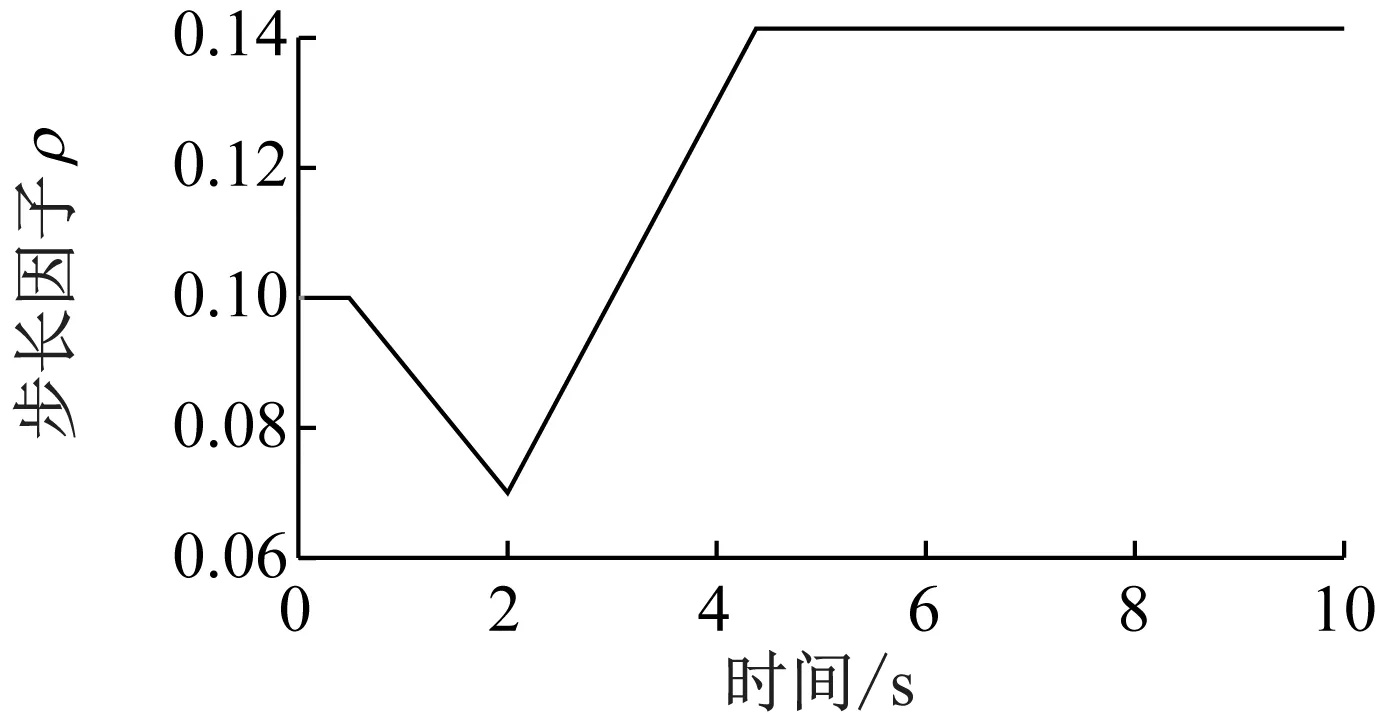
(d) 控制参数变化曲线图9 试验三仿真结果Fig.9 Simulation results of test three
4 结 论
本文针对发生碰撞的空间机械臂系统,研究其柔性臂杆的振动抑制。由于MFAC算法对参数初值的敏感性,使用模糊策略与传统无模型自适应控制相结合,提出了Fuzzy-MFAC方法。其中,制定模糊规则使其能实时为无模型自适应控制更新权重因子与步长因子。
仿真结果表明,模糊-无模型自适应控制方法相较于传统MFAC算法在振动抑制上有很大优势,振动衰减速率提高约34%,由频域分析得到振幅减小约42%。Fuzzy-MFAC方法简单、计算量小、反馈及时迅速的优点恰能为空间机械臂的碰撞问题提供有效理论支撑,具备极大的应用潜力。

