基于惯性传感器的输电线路舞动信号处理技术

胡 涛, 申立群, 雷 鹏, 张 博, 董伟锋, 刘梦瑶

(1.哈尔滨工业大学 仪器科学与工程学院,哈尔滨 150001; 2.国网河南省电力公司电力科学研究院,国网输电线路舞动防治技术重点实验室,郑州 450052)

随着全球气温升高和环境恶化的影响,近些年极端恶劣天气的发生次数逐渐增多,造成高压架空输电线路舞动灾害频发。输电线路舞动一般是在覆冰与风激励耦合作用下,形成低频高幅的自激振荡现象[1-4]。该现象可导致大范围的电路出现断股、相间闪络和损坏绝缘子等电路事故,给国家电力系统带来严重安全事故和经济损失。因此,输电线路舞动的监测与预防成为电力行业的研究热点之一。

输电线路舞动监测系统利用设备获取输电线路运动的有关参数来计算舞动特征参数,主要包含舞动幅值和舞动频率[5]。20世纪50年代,我国开始记载舞动相关事故,先后提出多种监测技术手段,包括视频跟踪技术、计算机三维仿真技术、线上传感器测量技术[6]。

目前,基于加速度计的舞动监测系统研究成果颇丰,加速度计跟随输电线路一起运动,对舞动特征参数进行实时测量,利用加速度二次积分获取舞动位置信息,但是这种监测系统仅适合测量包含垂向和水平振动的舞动类型[7]。文献[8]在单自由度舞动模型基础上,推导得到三自由度模型,阐述了加速度计测量舞动的数学机理,实现滤波和去除趋势项等信号处理算法,减小加速度测量过程中噪声和直流分量的影响,解决积分环节中初始位置确定和位移漂移问题。但是在实际应用中发现,随着输电线路运动,加速度计会随输电线路一起扭转,造成加速度测量值含有重力加速度分量,解算得到的位移和实际运动位移偏差较大。

因此,近年来基于惯性传感器设计的舞动监测系统发展迅速,惯性传感器中的陀螺仪可以解决输电线路扭转问题[9-14]。文献[15]提出采用九轴惯性传感器进行舞动监测,克服了加速度计受扭转干扰的问题,实现实时还原输电线路运动轨迹的姿态曲线还原算法,但算法中仅考虑了陀螺仪的零偏误差,系统的检测精确度还有待提高。文献[16]利用惯性传感器采集输电线路舞动的加速度和角速度,设计舞动定位算法实现了对输电线路舞动轨迹的还原,但并没有考虑对惯性传感器的误差进行分析和补偿。文献[17]为了实现实时准确输出输电导线的舞动轨迹,设计了MEMS惯性传感器的互补滤波算法和舞动轨迹的解算流程,但是未考虑到环境噪声对测量信号产生的影响。

为了实现对输电线路舞动特征参数的准确辨识,本文在基于惯性传感器的舞动监测系统上,提出一种舞动信号处理技术。基于已有的惯性传感器测量机理,对六轴惯性传感器进行误差标定与补偿,同时采用小波阈值去噪消除环境噪声,利用两向不水平度测定横滚角和俯仰角来计算初始四元数进行舞动信号的解算。最后,通过设计单摆实验来对舞动特征参数进行辨识和分析。

1 总体技术路线

舞动检测系统中,六轴惯性传感器与数据无线通信电路将封装于密封盒内,与输电线路进行固连,因此采用捷联惯性导航作为信号解算基本理论。陀螺仪和加速度计测量信号都处于惯性坐标系,需进行姿态解算获得导航坐标系下信号。针对高幅低频的非线性舞动信号,根据惯性传感器测量原理,分析环境和传感器自身各项误差来源,设计的输电线路舞动信号处理总体方案,如图1所示。

图1 输电线路舞动信号处理总体方案Fig.1 Overall scheme for galloping signal processing of transmission lines

输电线路舞动信号处理总体方案主要分为两大部分,分别是无误差舞动信号解算框架和实际测量误差消除。无误差舞动信号解算框架是舞动信号处理算法的基础,建立不考虑误差影响的舞动动力学模型,进行姿态解算和二次积分获取舞动姿态与位置信息,保证测量方案理论可行。实际测量误差消除通过分析测量过程中引入的各项误差来源,在误差引入的环节,设计相应算法抑制或消除误差项。

2 无误差舞动信号解算框架

2.1 三自由度舞动模型

对于导线的舞动,主要研究方法是首先研究导线的气动特性,计算风作用在非圆截面覆冰导线上的升力、阻力和扭矩。在此基础上,研究线路的舞动特性[18]。对于分裂导线,由于安装了间隔棒和防舞器,其舞动应该考虑导线结构产生的约束非线性和重力非线性,这使得舞动的影响因素更加复杂。

本文以典型覆冰输电线路单导线舞动作为研究对象,进行受力分析,建立舞动动力学模型。在覆冰导线截面受力分析中,只考虑舞动形成机理中受到的风力与重力的影响,忽略其余的阻力作用。单导线处于静平衡状态时,以质心平衡点C正下方位置O为坐标原点,建立参考坐标系,水平方向为x轴,竖直方向为z轴,质心水平位移为W,竖直位移为V,图2为覆冰导线截面受力分析图。

图2 覆冰导线受力分析Fig.2 Force analysis of ice-clad conductor

风力作用在覆冰截面不规则表面上,将产生沿相对风速Urel方向的阻力FD,在与相对风速垂直的方向上,形成升力FL作用在导线表面上[19-21],同时也形成扭转力矩FM作用于导线。根据现有空气动力学理论,结合覆冰导线风洞试验结果,三自由度覆冰导线上的风荷载向可表示为[22]

(1)

式中:ρ为空气密度,Urel为风速相对于导线的速度,d为输电线截面的特征长度,L为导线的长度,Cz、Cx、CM是与风攻角α有关的函数,分别为竖直方向、水平方向和扭转方向上的气动系数。由空气动力学理论可知,空气动力系数C(包含Cz、Cx、CM)可用三次多项式来近似拟合

C=a0+a1α+a2α2+a3α3

(2)

式中:a0、a1、a2、a3为拟合系数。

根据单导线绳索的偏微分方程,得到由竖向振动、水平振动与扭转振动耦合的三自由度舞动模型[23]

(3)

2.2 四元数姿态解算算法

根据四元数算法理论,设计舞动姿态解算流程如图3所示[24]。惯性传感器测得输电线运动加速度与角速度,利用角速度信号进行姿态解算,获取姿态矩阵;再将加速度信号进行旋转变换,依据比力方程消除重力加速度,得到导航坐标系下加速度。

图3 输电线路舞动姿态解算流程Fig.3 The calculation process of the galloping attitude of the transmission line

2.3 基于等效旋转矢量的姿态反演算法

姿态反演算法根据轨迹信息进行反向求解,获得惯性传感器模拟采样信号,是捷联惯导姿态更新算法的逆过程。假设已知姿态角和位置序列,通过逆向推导等效旋转矢量算法,实现惯性器件的高精度仿真和模拟。舞动信号姿态反演流程如图4所示。由导航坐标系的位置信息与姿态角信息,进行三次样条插值拟合。设反演所需初始参数值均为0,即姿态解算初始四元数为单位四元数,通过反演算法计算载体坐标系下的加速度和角速度信息。

图4 舞动信号姿态反演流程Fig.4 Dancing signal attitude inversion process

2.4 舞动信号无误差解算框架验证

在建立的三自由度舞动模型基础上,进行算例分析,获得理论舞动信息。在不考虑惯性器件测量误差和环境噪声时,对理论舞动信号进行反演与姿态解算,通过对比分析无误差解算框架的解算精度。

通常情况下,大跨距输电线路的跨中位置最易发生舞动,因此本节中舞动动力学模型都采用跨中位置进行数值解算。根据覆冰输电线路风洞实验结果,覆冰输电线截面的各项参数如表1所示[25-27]。

表1 覆冰截面输电线参数Tab.1 Ice-coated transmission line parameters

当覆冰导线的初始风攻角为10°时,利用参考文献[28]给出的空气动力拟合系数来对式(2)的动力系数进行拟合。

采用Newmark-Beta方法对三自由度模型进行计算,保证计算精度的前提下,采用合适的步长,可以得到模型的数值解。分别将表1和表2中对应的模型参数代入,得到位移时程图如图5所示。

表2 空气动力拟合系数Tab.2 Aerodynamic fitting factor

(a)

(b)

(c)图5 三自由度时程图Fig.5 Three degrees of freedom time history diagram

根据位移与姿态角时序信息,进行相应的时间窗处理,获取实际监测环境中单次处理的舞动信号时间序列,将其作为验证无误差解算框架的基准。对舞动时序信息进行反演,得到惯性传感器模拟采样输出信号。横滚角信号是已知基准,对其求误差可得如图6所示的横滚角反演误差曲线。

图6 横滚角反演误差Fig.6 Roll angle inversion error

由图6可知,整体反演算法引入的角度误差量级在10-11以内,远高于理论四元数解算精度,可认为反演算法引入的误差对姿态解算环节不产生影响。经过反演得到惯性传感器的模拟采样信号可作为姿态解算流程的输入信号,经过姿态解算流程可得到导航坐标系下加速度与姿态角信息。与原始基准信号相对比,得到如图7所示加速度误差曲线。

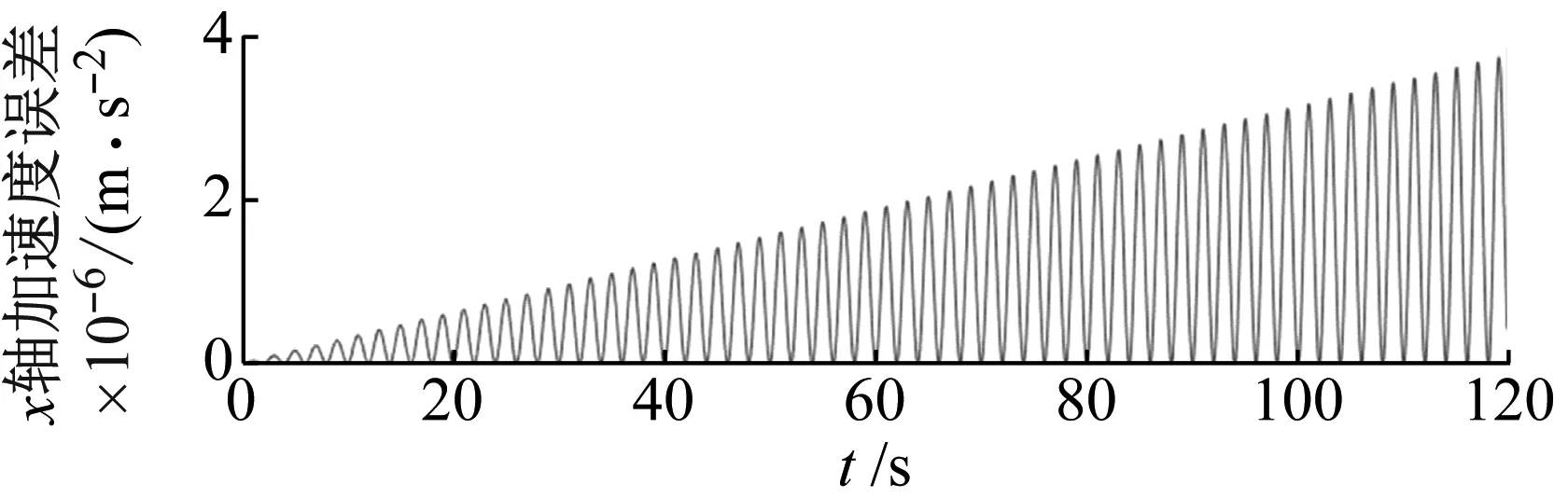
(a)

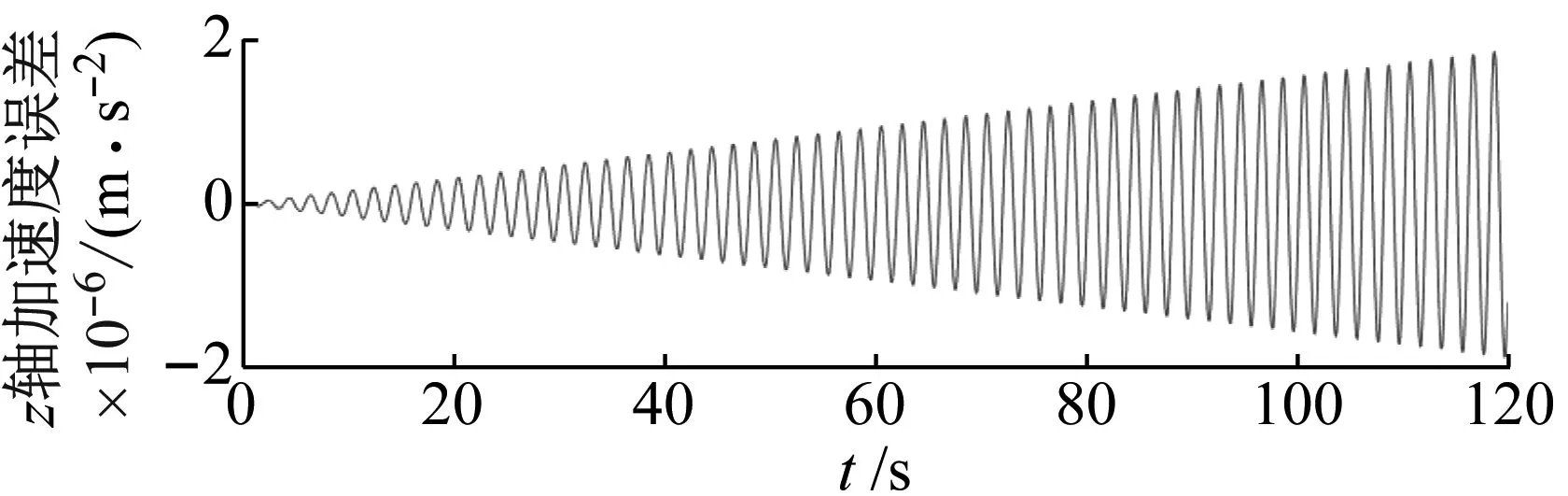
(b)图7 姿态解算加速度误差Fig.7 Attitude solution acceleration error

由图7可得,四元数对三自由度舞动信号的解算误差量级在10-6,那么120 s以内积分产生的位移误差对舞动幅值测量精度影响极小,解算结果具有较高准确性,证明六轴惯性传感器可有效消除舞动扭转角影响,获取正确舞动位移信号。同时导航坐标系下的x轴和z轴的加速度误差随时间递增,小于惯性传感器自身噪声影响。其中水平方向x轴的加速度误差并不对称,竖向z轴误差曲线保持对称。在一个周期内进行积分,z轴的位移误差会先增大再减小,而x轴位移误差将会不断增大。

3 实际测量误差补偿

3.1 惯性传感器误差模型

已知惯性传感器ADIS16470陀螺仪的测量范围为±2 000(°)/s,加速度计测量范围为±40g,同时提供±10g、±20g、±40g的可调加速度量程范围,可根据已知的导线舞动最大角速度和加速度来选用合适的量程范围。因此,无论是单导线或多分裂导线的舞动,本文采用的传感器均能正常检测。测量过程中,由于MEMS惯性传感器ADIS16470制造工艺精度有限以及环境干扰,导致测量信号中存在多种误差和噪声。本节通过归纳总结MEMS惯性传感器误差来源,建立加速度计和陀螺仪误差模型,分析误差对舞动解算精度的影响,研究相应的误差补偿技术,提高传感器测量精度。

确定性误差与测量信号间具有确定关系,可建立其与测量信号的数学表达式。根据实验室标定设备条件建立合适的误差模型,因此MEMS加速度计误差模型考虑不正交误差、零偏误差和刻度因数误差,陀螺仪误差模型考虑零偏误差、敏感加速度一次漂移和不正交误差。

当加速度计输出x轴加速度测量信号时,信号中含有y、z轴耦合加速度误差。加速度计x轴测量信号误差模型如式(4),其余两轴同理。

ax=Bf+K1x(fx+Kyxfy+Kzxfz)

(4)

式中:ax是加速度计测量值;f是各轴实际加速度输入;Bf是零偏误差;K1x是刻度因子误差系数;Kyx、Kzx是不正交误差系数。

当陀螺仪测量x轴角速度时,测量值中含有y、z轴耦合角速度误差,并且加速度对陀螺仪测量角速度也会产生干扰。陀螺仪动态性能好,一般其刻度因数误差量级较小,因此本文不考虑陀螺仪刻度因数误差,简化陀螺仪误差模型。陀螺仪x轴测量角速度信号误差模型如式(5),其余两轴同理。

D2xfy+D3xfz

(5)

3.2 无定向快速标定方案

无定向快速标定方案通过取消北向基准,减少测量位置档数,采用对称位置标定措施,同时结合部分出厂数据作为误差补偿参数。本文标定设备选用高精度大理石平台与方箱,进行快速标定,降低标定成本与设备要求。

采用表3所示的快速标定位置编排顺序,对x、y、z三轴方向进行变换,在8 min内完成对惯性传感器误差系数的一次标定。

表3 快速标定位置编排顺序Tab.3 Quick calibration position arrangement sequence

为避免标定中随机因素影响,采用6次标定结果平均值作为最终误差补偿系数,具有较好的补偿效果。表4为ADIS16470误差系数标定的平均值。

表4 ADIS16470误差系数标定平均值Tab.4 ADIS16470 error coefficient calibration average

采用软件算法,将参数标定值代入加速度计和陀螺仪误差模型中,对惯性传感器测量信号进行误差补偿,表5为标定前后各轴信号的测量结果。

表5 标定前后ADIS16470静态测量结果Tab.5 ADIS16470 static measurement results before and after calibration

3.3 小波阈值去噪实验验证

本文选择小波阈值去噪来对惯性传感器输出信号进行去噪处理。根据三自由度舞动模型解算得到的舞动信号为正弦信号可知,采用正弦信号作为仿真输入信号,可模拟舞动信号去噪效果。假设向仿真正弦信号中,添加高斯白噪声,使得原始含噪信号信噪比(SNR)为15 dB。根据信号噪声特点,以及考虑硬件实时处理能力,设小波分解层数为4,小波阶数小于8,采用各种小波基对原始含噪信号进行去噪处理。根据阈值Donoho模型计算固定阈值,针对原始含噪信号,采用不同小波基函数,得到表6基于不同小波基的小波阈值去噪信噪比对比。

表6 基于不同小波基的小波阈值去噪信噪比Tab.6 Wavelet threshold denoising signal-to-noise ratio based on different wavelet bases

由表6可知,采用db4小波基函数进行4层分解,信噪比为最大值,即去噪效果最佳。随着小波基阶数的增加,采用硬阈值与软阈值方法信噪比大小相同,此时信噪比主要与小波基阶数有关。然而,由数据增长趋势可知,阶数越大信噪比不一定越大,在阶数达到一定数值时,去噪效果开始减弱。选择每种小波基函数中信噪比最大的阶数,即db4、coif3、bior6、sym7,进行阈值原则的确定。

一般情况下,在无选取阈值原则时,阈值采用Donoho模型进行计算,选取阈值原则还包括Stein无偏似然估计(SURE)、启发式SURE阈值(Heursure)、最小极大方差阈值(Minimaxi)等。实际应用中,需要根据信号特征和噪声类型,选取最佳阈值原则。表7为各种阈值原则的信噪比对比。

表7 各种阈值原则的信噪比对比Tab.7 Comparison of signal-to-noise ratios for various thresholding principles

由表7可得,选择启发式SURE阈值原则(Heursure)效果最佳。同一阈值原则下,软阈值的去噪效果明显优于硬阈值。启发式SURE阈值软阈值结果与硬阈值结果相同,但为保证舞动信号平滑,优先选取软阈值启发式SURE阈值原则。原始含噪信号采用db4小波基及软阈值启发式SURE阈值原则进行去噪,结果如图8所示。

图8 db4小波软阈值去噪结果对比Fig.8 Comparison of db4 wavelet soft threshold denoising results

原始含噪信号经去噪处理,波峰与波谷噪声得到较好抑制,信号曲线平滑性得到改善。与不含噪的原始信号相比,去噪信号幅值存在部分不同,毛刺信号得到有效滤除。

3.4 两向不水平度测定

由于惯性传感器ADIS16470测量灵敏度有限,不能敏感地求角速度,无法采用重力加速度和地球角速度的双矢量定姿算法,进行姿态角初始对准。因此在姿态更新计算初始四元数时,可以将航向角初始值默认为0,通过两向不水平度测量获取俯仰角与横滚角初始值,进行后续舞动信号解算。

对各组加速度静态数据进行两向不水平度测定,可得到各姿态下的俯仰角与横滚角,计算其与拟定真值之间的绝对误差,确定两向不水平度测定算法精度。在水平和竖直放置的各种情况下,表8为两向不水平度测定实验计算结果。传感器姿态接近水平时,两向不水平度测定的角度精度最高,绝对误差绝对值最大为0.078 2°,均不超过0.1°;接近竖直位置时,精度较低,绝对误差绝对值不超过0.7°。因为正切函数在90°时存在跃变,极大影响计算结果精度。但在实际舞动监测中,输电线路自身材质较硬,输电线路仅在重力的作用下,俯仰角和横滚角达到90°属于极端情况,工程应用中不做考虑。因此,采用两向不水平度测定算法,可准确得到横滚角与俯仰角,满足课题使用要求。

表8 两向不水平度测定实验结果Tab.8 The experimental results of the two-way unevenness measurement

4 单摆实验验证

4.1 单摆实验设计

作为机械振动的典型物理模型,单摆运动规律与简谐运动基本一致,在摆动平面内有两个正弦位移信号和正弦摆角信号。因此,研究单摆运动可近似替代实际输电线路舞动,进行ADIS16470舞动监测信号处理技术的动态实验验证,分析所设计的信号处理算法实际应用效果。

本文实验使用的高精度单摆实验仪,该单摆专为测定惯性传感器精度设计,运动精度完全满足对舞动测量的精度要求。角度分辨率为1°,摆角最大可达90°,单摆悬线长度L为0.5 m。摆锤在重力的作用下,从初始摆角下落,做自由摆动,其频率计算公式为式(6)。代入数据得出单摆水平位移频率f的理论值为0.704 8 Hz,竖直位移频率为2f,即1.409 6 Hz。

(6)

动态实验首先将ADIS16470固连在单摆摆锤上,由直角尺进行校准。保证惯性传感器y轴方向与单摆摆动平面相互垂直,x轴方向对应竖直平面水平位移方向,z轴方向对应竖直位移方向。使用STM32单片机进行数据采集,USB串口通信进行数据传输,采样频率为200 Hz。实验前需要对ADIS16470进行预热30 min,采集一段时间静态数据。再将摆锤拉升至设定摆角对应的起始位置,松开摆锤,使其在重力的作用下做自由摆动,采样时间保持在3 min内。之后对测量信号进行信号处理和解算,即可得到位移与姿态信号,对其辨识获取幅值与频率,分析相对误差大小。

4.2 单摆实验解算结果分析

采用单摆信号进行舞动信号处理及特征参数辨识,以摆角为25°的单摆信号实验为例,对其信号处理过程进行详细分析。图9为ADIS16470的原始测量数据,此时数据均在载体坐标系下。

(a) 加速度信号

(b) 角速度信号图9 25°单摆运动测量原始数据Fig.9 25-degree pendulum motion measurement raw data

对原始数据进行误差补偿和去噪处理,经过两向不水平度测定确定初始俯仰角与横滚角。对单摆运动信号进行解算,得到一定时间窗内的导航坐标系下加速度以及姿态角信息如图10所示。

(a) 姿态角解算结果

(b) 导航坐标系加速度解算结果图10 25°单摆运动导航坐标系解算结果Fig.10 Calculation result of 25 degree pendulum motion navigation coordinate system

由图10(a)可知,横滚角信号曲线十分平滑,幅值随着时间增长不断衰减,频率基本保持不变。俯仰角在零值上下波动,最大值为0.569°。航向角与俯仰角的变化规律相似,其最大值为-0.213°,可知航向角和俯仰角波动范围均不超过0.6°。由图10(b)可知,导航坐标系下的加速度信号都关于x轴对称,重力加速度分量得到有效补偿,其中x轴与z轴信号变化趋势与正弦信号基本一致,噪声影响基本得到抑制,在波峰与波谷处存在少量毛刺;而y轴信号受噪声的影响比较显著,主要原因是所采用的单摆实验仪并不是理想的平面单摆,在下落的过程中存在y轴方向的振动,所以y轴信号也近似呈现振动信号的特征,具有一定运动频率。

利用导航坐标系下的三轴加速度,进行两次时域积分,可得到相应位移信号,图11为解算后位移时序信号。

图11 解算位移时序信号Fig.11 Solve the displacement timing signal

由图11可得,在随机噪声的影响下,实际解算的位移依然存在漂移现象。三轴位移均有不同程度的波动趋势,导致单向位移误差有所增大。图12是实际单摆解算的位移轨迹和理论计算的单摆位移轨迹对比,分别是摆动平面内的轨迹和空间轨迹。

(a) 摆动平面内轨迹对比

(b) 三维空间内轨迹对比图12 25°单摆运动信号解算轨迹对比Fig.12 25-degree pendulum motion signal solution trajectory comparison

由图12可知,单摆实验验证平面内三自由度舞动信号姿态解算的正确性,忽略次要运动信息。图中x轴向水平位移变化较大,与理论轨迹的偏离较为严重,z轴也有一定的偏移。因为原始信号中x轴信号中噪声明显大于z轴信号中噪声,噪声在积分过程中的累积效应较为明显,随着积分时间的增加而增大;同时单摆运动也会随着时间衰减,轨迹会逐渐收缩。整体空间轨迹围绕在理论轨迹附近,y轴存在一定的位移误差,范围在0.02 m以内。

其中在时刻t处,舞动轨迹的舞动幅值A(t)可由式(7)计算可得

A(t)=

(7)

式中:x(t)、y(t)、z(t)分别为x、y和z轴的位移大小;(x0,y0,z0)为参考点的坐标。

在较短的时间周期内,可将位移信号看作固定频率的正弦信号。采用最小二乘法,对一定时间内舞动信号离散数据进行正弦函数拟合,拟合后的舞动信号函数表达式如式(8)所示

(8)

式中:A为信号振幅;ω为角频率;φ0为初始相位;k偏移量。此时舞动信号的频率f为

(9)

改变摆角大小,进行多次实验,进行信号解算,得到如表9的多摆角单摆实验参数辨识结果,表中数据均为解算时间窗内误差达到最大的参数值。

由表9可得,实测幅值最大相对误差为3.58%,实测频率最大相对误差为3.67%,均满足舞动监测系统技术指标。随着摆角的增大,频率辨识精度有所下降,但幅值的测量精度有所上升。加速度信号积分获取位移信号的过程中,传感器引入的误差属于系统误差,量级可认为不变,在测量越大的位移时,积分时间不变的情况下,产生的相对位移误差将会变小,测量准确性将得到提高。因此,采用MEMS六轴惯性传感器ADIS16470测量舞动,在舞动范围为0.1～10 m,舞动频率为0.1～3 Hz时,采用本文所设计得信号处理技术,可准确的对不同摆角的单摆信号进行舞动特征参数辨识,为舞动监测和预防提供有效数据支撑。

表9 多摆角单摆实验参数辨识结果Tab.9 Parameter identification results of multi-angle single pendulum experiment

5 结 论

本文设计了惯性传感器舞动信号处理总体方案,介绍方案组成及其作用,得到主要结论如下。

(1) 建立单导线三自由度舞动模型,获得理论舞动信号曲线。由四元数更新进行姿态解算,由理论轨迹信息反向求解进行姿态反演。通过对比姿态反演与姿态解算,证明无误差解算框架的可行性。

(2) 分析测量误差来源,建立惯性传感器误差模型。利用高精度大理石平台与方箱,设计并验证了无定向快速标定算法,标定精度量级达到10-4。降低了传感器对北向基准的要求,实现快速标定。

(3) 确定采用启发式SURE阈值原则,进行四层分解的软阈值db4去噪效果最佳,有效地去除毛刺噪声,改善信号的平滑性。采用两向不水平度测定获得横滚角和俯仰角初值,满足后续姿态解算的精度要求。

(4) 采用单摆运动模拟实际舞动模型,验证航向角改变不影响加速度解算结果,对不同摆角的单摆运动进行解算,轨迹幅值相对误差不超过3.58%,频率相对误差不超过3.67%。验证平面内三自由度舞动信号姿态解算的正确性。

综上所述,本文设计的舞动信号处理技术可以较好的实现对舞动特征参数的辨识,对输电线路舞动监测系统性能的提升具有重要作用。