带内置可旋转隔板的调谐液体阻尼器减振性能试验研究

张蓝方, 谢壮宁, 周子杰, 彭肇才

(1.华南理工大学 亚热带建筑科学国家重点实验室,广东 广州 510640;2.广东现代建筑设计与顾问有限公司,深圳 518010)

现代高层建筑通常具有质量轻、周期长、阻尼小等特点,使得其对风荷载更加敏感,致使舒适度降低的同时也减少了非结构构件的使用寿命。在结构模态变形最大位置安装被动控制装置能够有效降低结构风致振动响应,具体形式包括调谐质量阻尼器(tuned mass damper, TMD)[1-2]和调谐液体阻尼器(tuned liquid damper, TLD)[3-7]。与TMD相比,TLD具有构造相对简单、造价低,且可兼做消防水箱等优势,因而受到越来越多的关注。

在水箱中设置阻尼构件能够使TLD阻尼比达到最优值,进而提升结构风振响应控制效果。Tait等[8]在TLD内安装了阻尼格栅,并分别采用线性与非线性数学模型描述水箱内液体晃动,与试验结果比对表明非线性模型能够跟准确预测流体在大振幅激励作用下的响应。Cassolato等[9]通过振动台试验研究发现能够采用调整阻尼格栅倾斜角度的方式控制TLD阻尼比的大小。谭平等[10]推导了内置可伸缩刚性挡板TLD的运动方程,计算机仿真分析表明挡板对结构提供附加阻尼明显。钟文坤等[11]分析了挡板宽度、挡板所在位置、水深比及激频比对水箱系统线性阻尼比的影响,结果表明激频比对阻尼比影响较大。Jung等[12]采用有限元方法研究了垂直挡板高度对流体晃荡的影响,研究表明挡板高度增加会导致其阻尼作用的减弱。Goudarzi等[13]对比了垂直挡板与水平挡板对TLD阻尼比的影响,结果表明水平挡板对细长水箱阻尼增大作用明显,垂直挡板对宽水箱阻尼增大作用明显。

对于结构-TLD耦合系统,TLD的固有频率与结构受控模态频率相近时控制效果最佳,与结构频率相差较大时将失谐。针对可能存在的TLD失谐,Zahrai等[14]期望通过在TLD内设置可旋转隔板,并调节隔板角度的方式调整TLD频率,进而弥补失谐所带来的影响,从而解决TLD工作频带较窄的问题,TLD自由振动试验结果表明当隔板角度小于75°时,频率随着角度增加而不断增大。但Love等[15]针对十字形叶片形式阻尼构件的研究表明,TLD频率受内部阻尼构件所产生的附加质量的影响而减小,且频率的减小幅度随着构件宽度的增大而增加,可见Zahrai和Love针对频率变化趋势的结论不同、相互矛盾。

尽管对TLD内部构件水动力特性已经有一些研究,但已有相关研究所发表的公开成果尤其是可旋转挡板的依然偏少,JGJ/T 487—2020 《建筑结构风振控制技术标准》[16]也仅提供了阻尼网作为增加水箱阻尼的手段,这些成果和建议还远不足以支撑TLD设计的需要,同时针对构件本身的调谐性能的研究结论仍存在矛盾之处,这些问题需要进一步开展深入有效的细致研究。

本文以工程中常见的矩形平面TLD为例,按缩尺比1∶10设计制作TLD试验模型,采用白噪声激励的振动台试验方法,研究TLD内置可旋转隔板对TLD固有频率和阻尼比的影响,具体影响参数为隔板和晃动方向夹角,以及隔板安装位置。采用信号解耦技术对试验测得的水箱液面多点响应信号进行解耦分离,再采用不同识别方法识别TLD性能参数,并与已有研究结果进行比对,讨论了可旋转隔板的阻尼特性和调谐性能的局限性。

1 内置可旋转隔板TLD

隔板是一种能够阻碍流体沿TLD控制方向运动的竖向阻尼构件,在TLD内的设置形式如图1所示,每块隔板可以竖向中心线为轴在0°～90°范围内转动。当隔板处于完全开启状态时(即隔板平行于TLD控制方向),整个水箱作为单个TLD工作;当隔板处于完全关闭状态时(即隔板垂直于TLD控制方向),整个水箱被隔板分隔成为多个TLD。

图1 内置旋转隔板TLDFig.1 TLD with rotatable baffles

2 振动台试验

2.1 试验模型

按照缩尺比1∶10设计了TLD试验模型如图2所示,相关变量的相似准则在表1中列出,选取大尺寸模型的目的是减小缩尺效应影响,确保试验结果的真实性和可靠性。水箱净空尺寸L×B×h(长×宽×液深)为2.1 m×0.64 m×0.44 m,采用钢板和PC板制作。模型液深比h/L=0.21>0.125,故为深水TLD,根据深水TLD理论,矩形平面水箱内液体晃荡的第j阶频率为[17]

表1 相似准则Tab.1 Similitude law

(a) 带隔板TLD(一列)

(b) 带隔板TLD(两列)图2 TLD模型尺寸Fig.2 TLD model dimension

(1)

式中,g为重力加速度。由式(1)计算可得模型前3阶模态频率分别为f1=0.46 Hz、f2=0.8 Hz和f3=1.04 Hz。共设计了2种隔板位置方案,一列隔板方案(图2(a))将隔板设置在L/2位置处,两列隔板方案(图2(b))将隔板设置在L/3、2L/3位置处,每列隔板由四块塑料板组成,每块隔板长0.7 m、宽0.16 m、厚0.02 m。

2.2 试验装置、加载方式和响应测量[18]

采用振动台试验的方法研究带隔板TLD的减振性能,试验装置和模型如图3所示。

目前，计算机信息技术已被广泛应用到各个领域中，但在文件档案的管理上仍有部分地区相对较为传统，并没有真正落实现代化管理模式，即便已经引进了现代化设备，但却没有做好局域网的资源共享，在文件档案的管理上仍采用传统的手工抄写和统计方法，加剧了档案管理出错的概率。

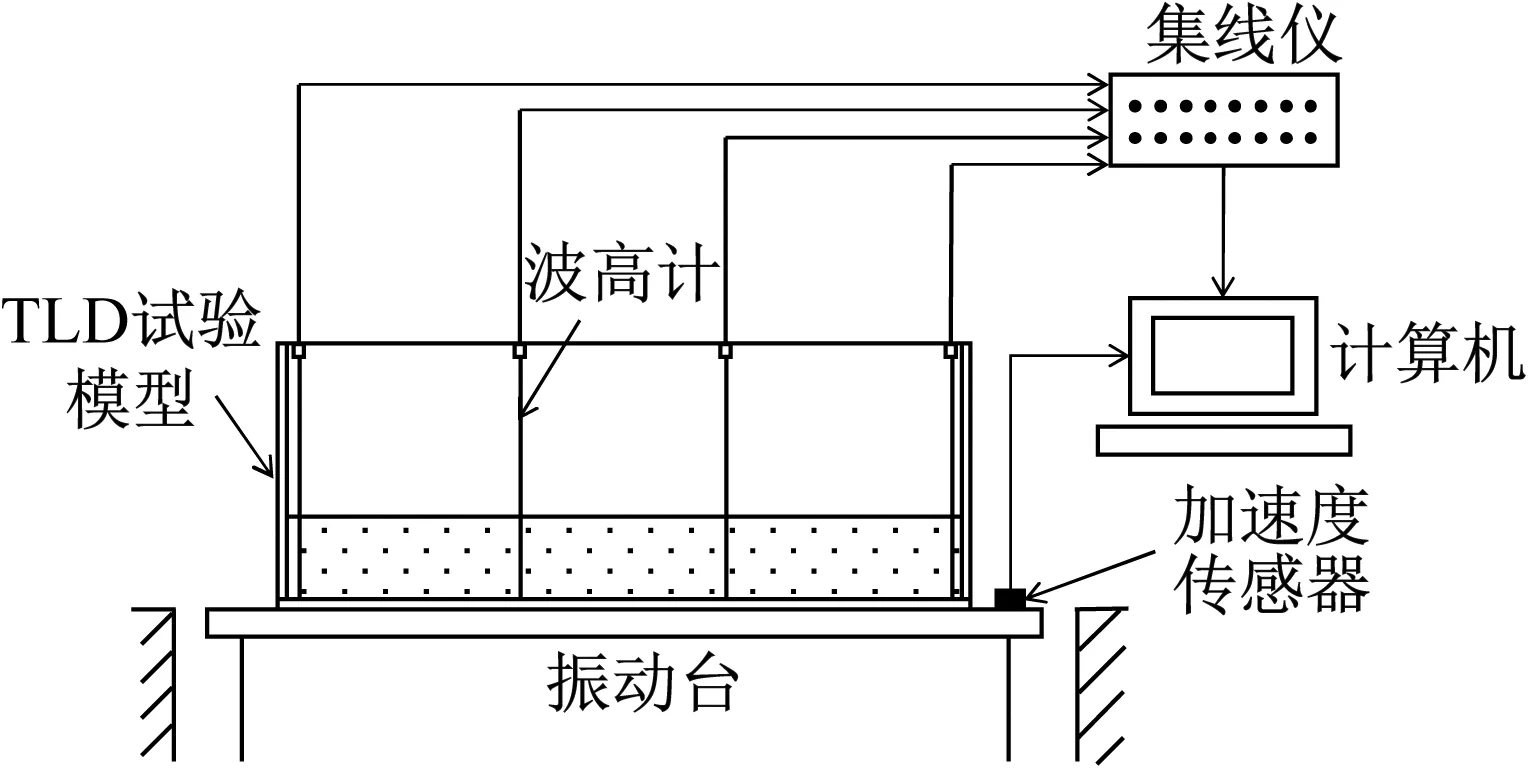
(a) 试验装置示意图

(b) 振动台上TLD模型示意图图3 试验装置Fig.3 Test setup configuration

试验所使用振动台为Servotest公司生产的3向6自由度地震模拟振动台,加载模式只限于位移加载。根据试验模型前3阶模态频率大小,确定目标加速度激励为有限带宽0.2～3 Hz的白噪声激励。采用随机模拟的方法生成与目标加速度激励相对应的位移激励,并沿着TLD模型x轴方向进行单向加载。水箱内自由液面高度变化由4支数字波高计测量,采样频率为100 Hz,其中2支波高计靠近水箱壁设置而另2支靠近水箱中心设置,用以描述沿水箱长度方向的整体液面变化情况。振动台台面加速度由一支加速度传感器测量,采样频率为25 Hz。

2.3 试验工况

本文共进行14个工况试验,分别对应隔板角度为0°、15°、30°、45°、60°、75°和90°,同时分别对应两种隔板位置为L/2和L/3+2L/3。所施加位移激励相对幅值大小均为Λ=0.001 8,其中Λ=σe/L,σe为位移时程均方根值。每个试验工况加载时长均为5 min。

2.4 参数识别方法

采用复数形式的二阶盲辨识(SOBI)方法[19](CSOBI)对波高计测得的TLD耦合响应信号进行解耦得到模态振型,再对解耦后的模态响应信号进行参数识别得到TLD模态频率和阻尼比。参数识别方法采用改进的贝叶斯谱密度法[20](MBSDA)和曲线拟合方法。MBSDA与曲线拟合方法均假设模态坐标下激励的功率谱密度函数为

(2)

式中:S0为输入激励在TLD固有频率处的功率谱密度值;λ为荷载指数;fj为TLD内液体晃荡的第j阶频率。解耦后的模态响应信号与模态激励功率谱密度的关系为

(3)

(4)

δ(fj,ζj,S0,λ)=

(5)

式中:Δf为离散频率点的频率间隔;(n1Δf,n2Δf)为拟合频率范围;ζj为TLD第j阶模态阻尼比,通过求残差平方和最小可以得到S0、λ、fj和ζj。

3 试验结果分析与讨论

3.1 试验结果

对试验测得的波高响应信号进行模态解耦后再分别采用MBSDA和曲线拟合法进行参数识别,以确定S0、λ、TLD频率和阻尼比。将参数识别结果代入式(2)和式(3),能够得到TLD1阶模态波高响应功率谱密度。

在相对激励幅值Λ= 0.001 8作用下,研究隔板设置位置(L/2、L/3+2L/3)与角度(θ=0°、15°、30°、45°、60°、75°、90°)对TLD减振性能的影响,图4、图5展示了部分工况1阶模态波高响应功率谱密度的试验结果与参数识别结果的对比。由图可知,除θ=60°工况外,其余各工况参数识别结果与试验结果吻合良好,说明参数识别结果的准确性;θ=60°工况参数识别结果与试验结果存在较大误差,这是由于随θ增大隔板对1阶模态响应抑制作用增强,使得该工况1阶模态频率所对应谱峰值很小,此外信号本身所存在随机性,导致1阶模态频率和阻尼比的识别难度增加,这也是两种方法的识别结果偏差较大的主要原因。除此之外,由图4、图5可知,当θ<60°,波高响应峰值对应频率小于f1=0.46 Hz,而当θ>60°,响应峰值对应频率大于f1。

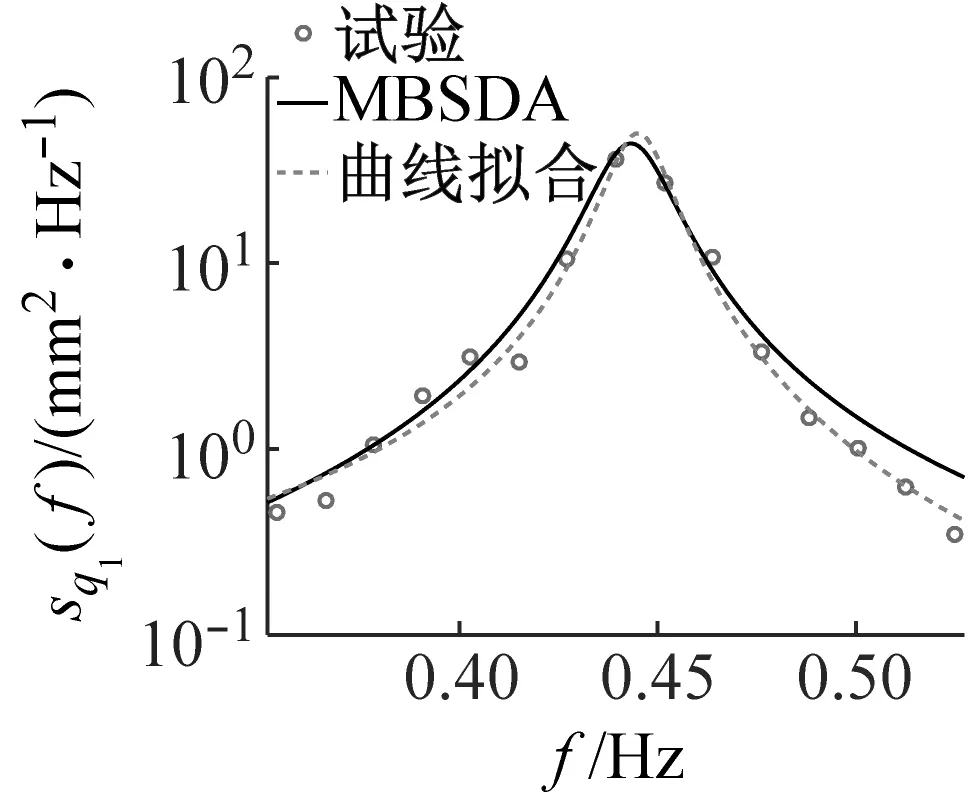
(a) θ=30°

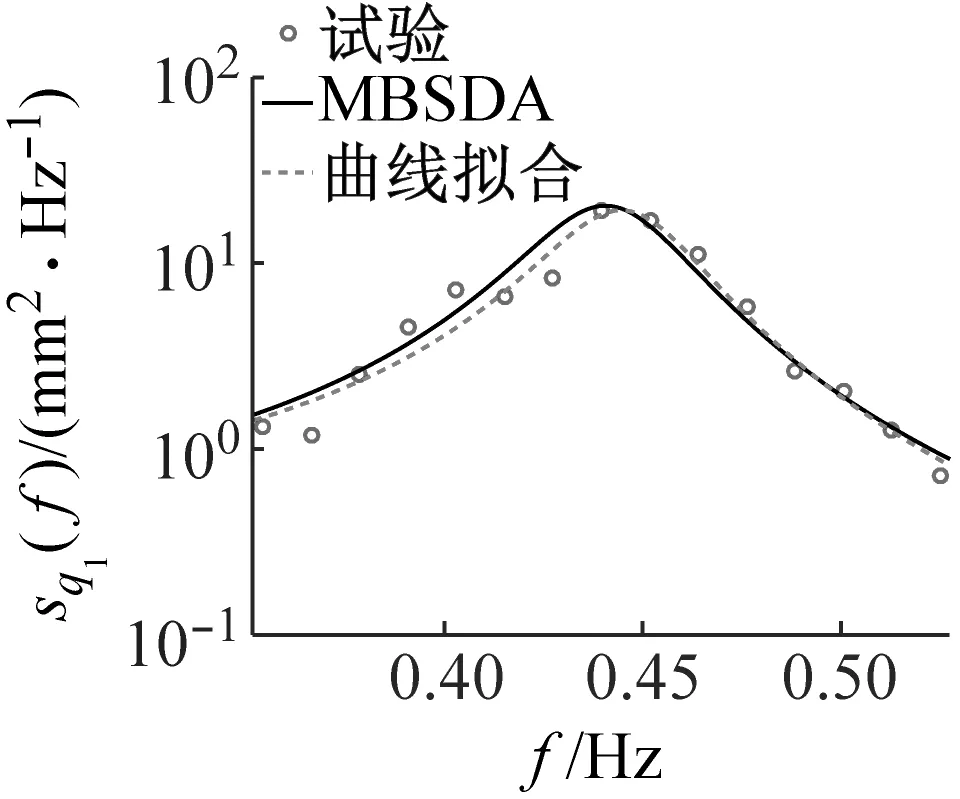
(b) θ=45°

(c) θ=60°

(d) θ=75°图4 带一列隔板TLD试验结果与参数识别结果比对Fig.4 Comparison of experimental to parameter identification results of TLD with one row of baffles

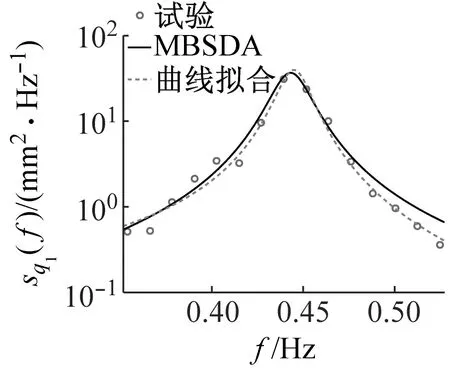
(a) θ=30°

(b) θ=45°

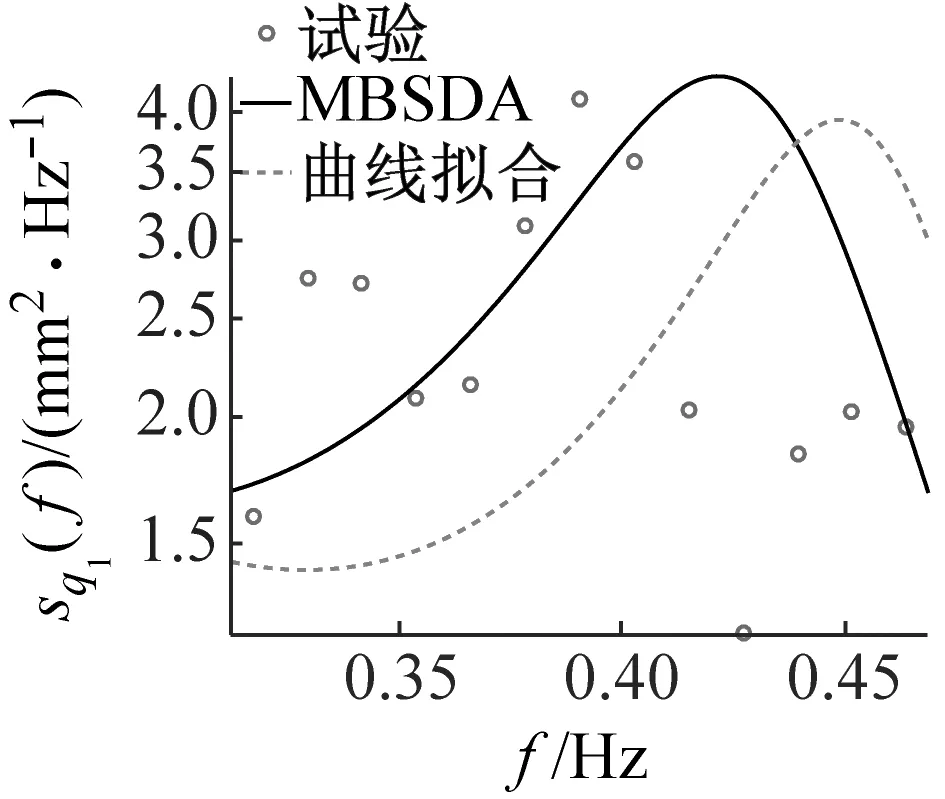
(c) θ=60°

3.2 固有频率

进一步考察带隔板TLD固有频率随θ的变化规律,将TLD模型固有频率试验结果在表2中列出。由表中数据可知,除θ=60°工况,两种方法识别结果基本相同。当θ<60°时,TLD固有频率受隔板所产生的附加质量影响而小于f1,且固有频率随θ增大略有减小。当θ=60°时,和1阶模态对应的模态响应较弱使得其模态响应谱(图4(c)、图5(c))呈现较大的随机离散性,导致两种方法的识别结果存在较大差异。当θ=75°时,由于阻尼的增大完全抑制了1阶模态响应,识别得到的是高阶模态的频率,对于带一列隔板TLD此时的频率为2阶模态频率,相应对于带两列隔板TLD则为3阶模态频率。由固有频率变化趋势可见可旋转隔板不能用于解决TLD工作频带较窄的问题,也不能用于补偿可能存在的TLD失谐。

表2 TLD模型固有频率试验结果Tab.2 Experimental results of the natural frequency of TLD model

以一列隔板为例,采用CSOBI方法解耦得到θ=60°、75°时两种工况对应的1阶模态振型分别为[-2.591 -1.302 7 1.357 9 1.973 1]T和[-2.481 1.152 9 -1.235 3 1.802 1]T。可见θ=60°的模态形状还是属于1阶振型,而θ=75°的模态形状已和未设置隔板水箱的第3阶振型相近。这是因为θ=75°时隔板阻隔作用已十分明显,水箱几乎被分隔为2个小水箱,根据式(1)可知在L减小、h不变的情况下频率将变大。因此,隔板的分隔作用是固有频率增大的主因。

将本文试验结果与文献[14]结果进行对比,如图6所示。图中ω′为各工况模态频率与θ= 0°工况固有频率的比值,其中点划线为1阶模态频率比变化曲线,图6(a)、6(b)中双点划线分别为2阶、3阶模态频率比变化曲线。由图更清晰、直观可见隔板设置位置不影响模态频率变化趋势。由于本文是以θ每15°设置一个试验工况,故当隔板角度在60°与75°之间时,用虚线表示此区间内固有频率变化的不确定性。而文献[14]结果显示隔板在0°～75°范围内转动时,液体晃动频率呈连续增大趋势,且在45°时增幅最大。

(a) 一列隔板

(b) 两列隔板图6 带隔板TLD模态频率Fig.6 Modal frequency of the TLD with baffles

值得注意的是,与本文所采用试验方法不同,文献[14]对TLD试验模型进行脉冲激励下的自由振动试验,并在物理坐标下分析所测信号获得液体晃荡频率。将本文试验中由波高计ch1所记录的θ=30°～90°工况带隔板TLD耦合响应功率谱密度展示于图7中,由于隔板设置在TLD的3阶模态节点处,故2阶模态(即f2=0.8 Hz)被明显抑制。由图7可知,随着隔板角度增加,隔板使液体晃动的1阶模态响应逐渐减小,当θ=30°时1阶模态对应谱峰值大于3阶模态,而当θ=45°时1阶模态对应谱峰值远小于3阶模态。这意味着3阶模态频率将被识别为液体晃动频率,这也是文献[14]的试验结果在θ=45°时大幅增大的原因,θ=60°工况情况与之相同。注意到,两列隔板方案在θ≤30°时,本文试验的频率值均是随θ的增大单调递减的,这符合θ增大迎流面变宽,隔板的附加质量增大而导致频率下降的规律,而文献[14]的结果正好相反,这显然是不合理的。

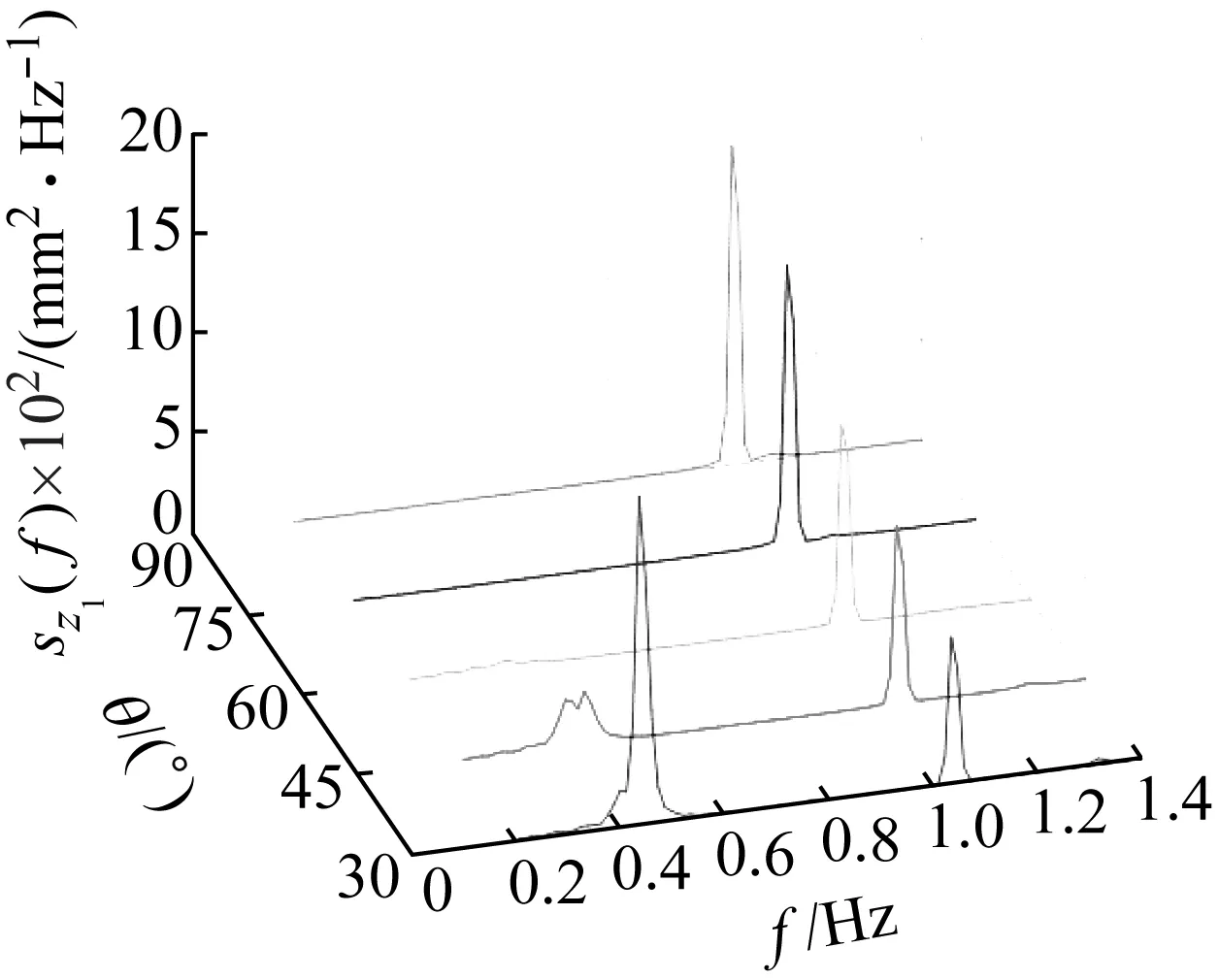
图7 带两列隔板TLD波高响应功率谱密度Fig.7 PSD of the wave height response of fluid in the TLD with two rows of baffles

3.3 阻尼比

隔板角度θ的变化对1阶TLD模态阻尼比的影响如图8所示。由图8可见,MBSDA识别结果略大于曲线拟合方法,当θ<60°时,阻尼比随θ增大而增大。当θ=60°时,由图4(c)、图5(c)可知波高响应功率谱密度曲线形状不规则、数据离散,导致该工况阻尼比识别结果间存在较大差异。当θ>60°时,水箱被隔板分隔,原1阶模态消失,渗流是阻尼的主要产生方式,且随着隔板的关闭(θ趋近90°)渗流逐步减弱,显示阻尼比随θ增大而减小的变化趋势。但对于带一列隔板TLD,隔板几乎关闭时(θ>60°)阻尼比依然相对偏高(大于4%),这是由于隔板并没有严格起到隔断的效果,即便是θ=90°时隔板两端的液体之间还是有渗流产生;与之相比,θ>60°时两列隔板方案的阻尼比减小到2%以下,远小于一列隔板方案结果,这是因为隔板数量增多使得隔板对液体隔断效果增强,隔板两端的液体之间渗流减弱。

(a) 一列隔板

(b) 两列隔板图8 带隔板TLD的1阶模态阻尼比Fig.8 First-order modal damping ratio of the TLD with baffles

对曲线拟合方法识别的阻尼比进行多项式拟合,由图8可知,在常用阻尼比取值范围内(即θ=15°～45°)拟合结果与试验结果吻合良好。值得注意的是,当θ在30°～45°范围内时,两种方案的阻尼比大致在2%～6%之间,这个区间通常是TLD的最佳阻尼比范围。因此,采用旋转隔板可以较容易实现对TLD阻尼比的调节,但θ不宜超过45°。

4 结 论

由本文研究可以得到以下结论:

(1) 当隔板角度θ小于60°,TLD的1阶模态频率受隔板所产生的附加质量影响而减小,且减小幅度随θ增大而增大;当θ等于75°,隔板的分隔作用使1阶模态频率大幅度增加,晃动呈高阶模态形式;设置一列或两列隔板不影响固有频率变化趋势。

(2) 隔板能够减小TLD的1阶模态响应,当θ小于60°时,1阶模态阻尼比随θ的增加而增大,通过对θ调节可获取TLD控制所需的最佳阻尼比,但θ不宜超过45°。

(3) 可旋转隔板对TLD固有频率的影响与已有研究所给出的频率随着θ增加而不断增大的结论有本质差别,证明已有研究结论是不严谨的,说明在TLD内设置可旋转隔板不能有效应对TLD失谐问题。