基于地面保障流程的过站航班延误预测方法

羊 钊,陈怡欣,张智杰

(1. 南京航空航天大学 通用航空与飞行学院,江苏 溧阳 213300; 2. 南京航空航天大学 民航学院,江苏 南京 211116)

0 引 言

航班作为延误发生的载体是研究者们一直以来研究的重要对象[1]。航班延误的产生机理复杂多样,与机场网络[2-3]息息相关,对航班延误进行提前感知和准确预测,需要综合考虑多方因素。现有的研究方法可分为两大类。由于延误状态来源于正常状态的跳转,分析状态之间的转移概率成为此方向的一个切入点。将经典数学分布与航班出发延误时间和到达延误时间相结合[4],能够模拟出航班延误产生与消散的过程,进而对其进行预测;采用贝叶斯网络[5]或将其与前序后序航班的链式波相结合[6-7],可以反映出航班间延误的相互影响,进而调整航班计划以减轻延误。由于机器学习和数据挖掘方法可从大量历史数据中直接预测出航班延误状态,利用数据挖掘规律成为此方向的另一切入点。将多种与航班延误相关的特征如自动相关监视广播(ADS-B)特征[8]、恶劣天气特征[9]、机场交通复杂性(ATC)特征[10]等进行融合,采用KNN[11]、随机森林[12]、聚类[13]等方法建立由输入端到输出端的预测模型。该方法避免了模型对各种信息的完整需求以及延误产生机理方程的构建等问题。因此,机器学习领域的诸多经典模型以及各种改进的深度学习模型[11,14-16]被广泛应用于航班延误预测方面。

在航班延误频繁发生的航班过站保障流程中,利用过站航班相关数据有助于辨识延误发生的源环节,提高航班保障作业时的延误预测精度。然而由于数据难以采集利用、多方交织参与作业、航班特征难以提取等困难,上述提及的两类研究方法均未对此阶段航班延误问题开展研究。利用概率研究航班延误的方法中,只将航班的上下游延误时间分布联系起来;利用机器学习模型研究航班延误的方法中,只将与航班间接相关的特征进行融合,并未考虑航班延误的来源。

基于上述思想,笔者从新的视角展开对航班延误预测的研究。首先,根据航班流程节点的时间特征统计相邻前序-后序流程节点的时间差及标准范围,处理后作为模型输入特征;其次,根据过站航班的地面保障服务流程,构建神经网络拓扑结构,具体来说,每个过站航班的保障节点被表示为神经网络中的一个节点,相邻流程的连接被表示为一条有向边;最后,构建了两类航班延误预测模型,第 1 类包括随机森林、决策树、XGBoost 3 种传统的机器学习模型,第 2 类为 4种图卷积神经网络模型,包括图卷积网络(GCN)、图注意力网络(GAT)、GraphSAGE网络以及集成图卷积网络模型。4 种图卷积神经网络模型将图神经网络结构与过站航班作业流程融合,利用图网络结构上不同层间多种特征聚合、更新和传递的方式,以期提高航班延误预测的精度。

1 数据准备与预处理

考虑过站航班流程节点的先后逻辑,收集并清洗机场内航班保障流程的时刻数据,根据开舱门时刻与后续流程节点是否属于同一天,将航班数据划分为隔夜航班集合和非隔夜航班集合。在两类集合中分别计算出每条航班实际起飞时刻与计划离港时刻的差值集合,将两类集合分别划分出延误航班集合和非延误航班集合,即隔夜延误航班集合、隔夜非延误航班集合、非隔夜延误航班集合、非隔夜非延误航班集合。对每个集合计算出航班后续-前序流程节点的时间差值,在隔夜非延误、非隔夜非延误的航班集合中计算相邻节点时间差,作为标准时间段集合。将隔夜延误、非隔夜延误航班集合中的节点差值与标准时间段集合进行对比,得到两类延误航班与标准时段集合的距离节点特征集合,作为后续模型的输入特征。

1.1 数据逻辑处理

航班过站时一般性过站流程如图1。

图1 航班过站流程示意

此流程可分为 3 个部分:①与旅客相关的流程;②与货物行李相关的流程;③飞机本身需要进行保障的流程。由于目前的技术手段对货物行李和飞机保障两部分的流程时刻收集存在困难,因此笔者采用与旅客相关的时刻节点进行后续实验。具体选取上海浦东国际机场2019年6月1日—12月31日内 94 262 条过站航班保障流程节点的时刻数据,其中延误航班数据 22 270 条,非延误航班数据71 992条。采集的节点包括计划进港时刻、实际落地时刻、实际上轮挡时刻、开舱门时刻、关舱门时刻、登机口开启时刻、登机口关闭时刻、实际撤轮挡时刻、实际开始滑行时刻、实际起飞时刻、计划离港时刻,如图2。

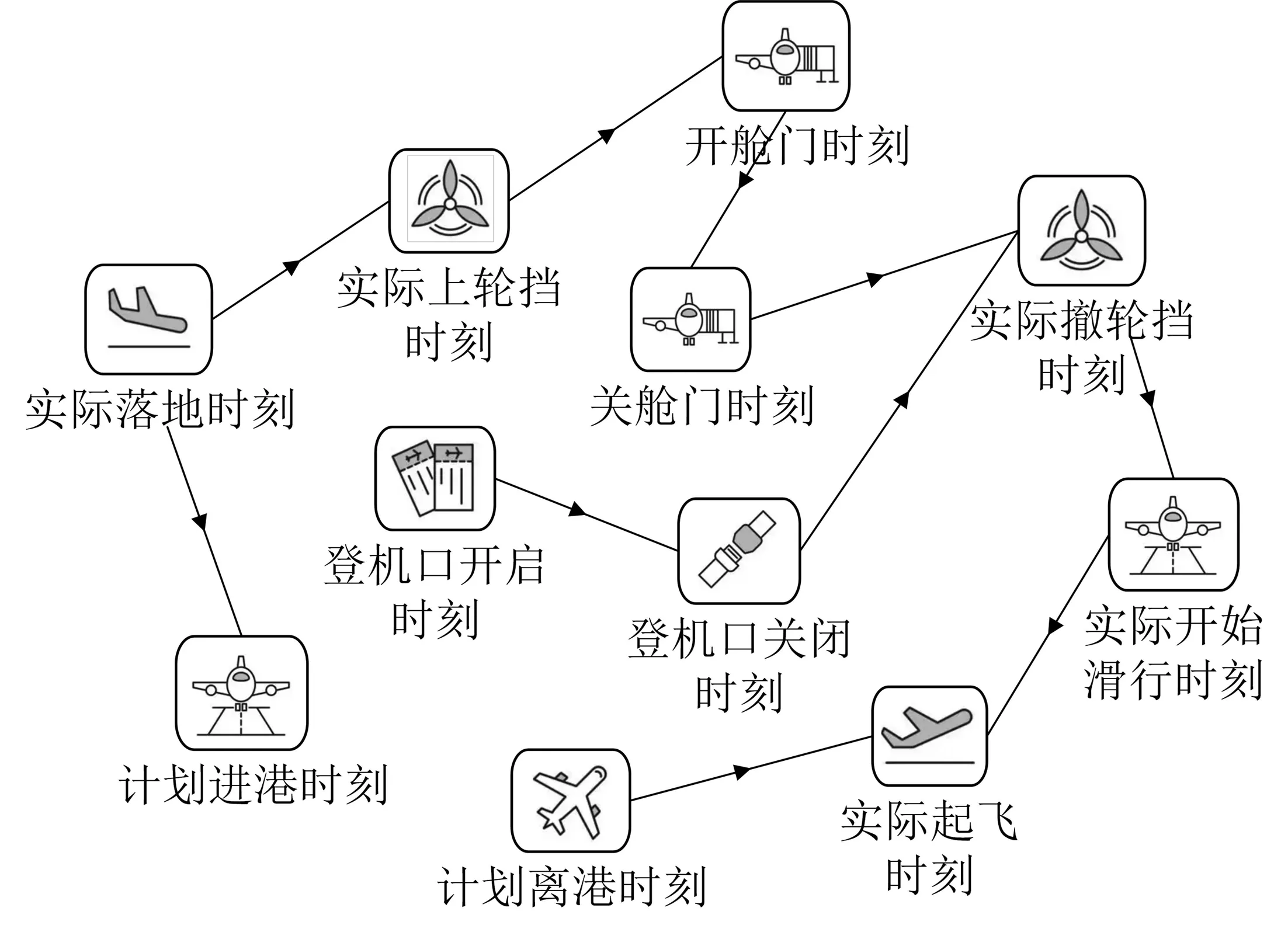
图2 数据示意

由于选取的时刻集合存在前后逻辑关系,需要进行数据逻辑处理,处理原则为:

1)检查采集到的各航班时刻的前后关联,将时刻数据中的异常值剔除,如该航班的某一时刻与其余时刻不在同一天,该航班的下一时刻比上一时刻早等。

2)由于存在隔夜起飞情况,根据每条航班中开舱门时刻和关舱门时刻差值长度,将差值长度超过 400 且开舱门时刻在晚上、关舱门时刻在第二天早上的数据归为隔夜航班集合Tpover,其余数据归为非隔夜航班集合Tpnonover。

3)以各航班的实际落地时刻tal、计划进港时刻tea、实际起飞时刻tad和计划离港时刻ted为航班的参照执行时刻,优先处理与实际落地时刻和实际起飞时刻接近的异常和缺失时刻。将需处理的时刻数据分为两类:一类与该航班实际落地时刻tal或实际起飞时刻tad相关,另一类与该航班前后两个及以上时刻相关。针对两类异常值和缺失值,在Tpover和Tpnonover中,利用与其余流程节点上完好时刻数据的关系进行清洗。

笔者用两类问题节点举例说明。

1)第 1 类异常值使用实际开始滑行时刻进行说明,如果第i条航班的实际开始滑行时刻ti-at缺失或异常,重新计算出的第i条航班的实际开始滑行时刻t′i-at如式(1):

(1)

式中:ti-ad为第i条航班的实际起飞时刻;ti-at为第i条航班的实际开始滑行时刻;pnonover和pover分别为非隔夜航班和隔夜航班的航班条数。

2)第2类异常值使用实际关舱门时刻进行说明,如果第i条航班的实际关舱门时刻ti-cd缺失或异常,重新计算得到的第i条航班的实际关舱门时刻t′i-cd如式(2):

(2)

式中:ti-boff为第i条航班的实际撤轮挡时刻;ti-od为第i条航班的实际开舱门时刻。

将清洗后的所有时刻数据作为原始数据集合Tp,其中Tp包含Tpover和Tpnonover。

1.2 数据特征抽取

为得到非延误航班各流程的标准时段,计算Tp中所有航班实际起飞时刻与计划离港时刻的时间差集合M,如式(3):

(3)

式中:di为第i条航班实际起飞时刻与计划离港时刻的时间差;ti-ad为第i条航班的实际起飞时刻;ti-ed为第i条航班的计划离港时刻;tr为机场实际起飞时间和计划离港时间之间可接受的时间差,tr为常数。

在Tpover和Tpnonover中,分别划分延误航班时刻集合Tdelay和非延误航班时刻集合Tnon-delay,如式(4):

(4)

基于航班中存在的隔夜和非隔夜起飞情况,分别计算Tdelay和Tnon-delay中航班各前序—后序流程节点上的时间差值集合δdelay和δnon-delay。选取各时间差的上四分位数QU和下四分位数QL的数据段为标准时段集合Dstd,选取时间差如表1。

表1 前序—后续流程节点时间差数据统计

将Dstd与Tdelay中的δdelay进行比较,得到距离集合X如式(5)、式(6):

X={x1,x2,…,xis,…,xpdelay×(m-1)}

(5)

(6)

式中:m为一条航班包含的流程节点个数。距离集合X的特征即表1中的第一列特征,随后将距离集合作为图卷积神经网络模型的输入特征。

2 模型建立

将航班流程节点转化为图网络结构,将其细化成模型需要的边集合、索引集合、节点特征集合和预测值集合,构建图卷积神经网络模型。

2.1 图网络结构建立

笔者使用延误航班各流程节点构建图网络结构G=(V,E),其中,va∈V,V={v1,v2,…,vn}为由va构成的点集合;E={e1,e2,…,epdelay×(m-1)}为(va,vb)构成的边集合;V、vi分别为G中的节点集合和第i个流程节点;E、ei分别为G中的边集合和第i个边;pdelay为延误航班的航班条数,每条航班构成的图网络结构中包含m-1条边。G的邻接矩阵Aab和度矩阵Dab中的元素Aab、Dab如式(7)、式(8):

(7)

(8)

式中:n为所有延误航班的总流程节点个数。

2.2 多种图卷积神经网络层建立

2.2.1 GCN 层

搭建GCN(graph convolutional networks)卷积层[17]进行图网络结构上节点特征的聚合、更新和传递,使用传播规则f(·)将图上特征向下传递,传递过程如式(9):

X(l+1)=f(X(l),Aab)

(9)

式中:X(l)为第l层的特征;f(·)为图网络结构G层间的传播规则。

根据式(10)的卷积定理得到图卷积过程如式(11);根据拉普拉斯矩阵的性质L=UΛUT,该公式可进一步改写为式(12);引入切比雪夫多项式拟合卷积核,对图卷积公式取一阶近似,得到图卷积公式如式(13);图神经网络中GCN卷积层之间的传播过程如式(14):

(10)

(X⊗Wθ)G=U[(UTWθ)·(UTX)]

(11)

(Wθ⊗X)G=Wθ(L)X

(12)

(13)

(14)

式中:Wθ为可学习的参数;In为G的自循环;L为G的拉普拉斯矩阵。

2.2.2 GAT 卷积层

GCN卷积层在聚合、更新和传递特征时,难以分配不同权重给不同邻居节点。搭建GAT(graph attention networks)卷积层[18],通过注意力系数改进上述缺点。

分别计算vi与多个邻居节点之间的注意力权重。vi到每个邻居节点vj的相关性系数eij如式(15);之后计算注意力系数αij如式(16);把节点上的时间特征加权求和,得到vi上的新时间特征x′vi如式(16):

eij=a([wxvi‖wxvj]),vj∈Vi

(15)

(16)

(17)

式中:xvi、xvj为vi、vj的输入特征;w为不同节点上可学习的参数;a为特征映射函数;f′LeakyReLU(·)为激活函数;x′vi为vi上的新时间特征;eij为vi到每个邻居节点vj的相关性系数;αij为vi到每个邻居节点vj的注意力系数。

最后,通过GCN卷积层进行每个流程节点上时间特征的聚合、更新和传递。

2.2.3 GraphSAGE 卷积层

GCN卷积层需要对整个图结构进行迭代,搭建GraphSAGE(graph sample and aggregate)卷积层[19]。通过邻居采样将流程节点的全图训练模式转化成以各流程节点为中心的小批量训练模式,避免相同时间特征多次训练。

(18)

∀vj∈Vi

(19)

(20)

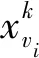
结合文中所述特征和预测任务的特殊性,构建双层图卷积神经网络(双GCN层、双GAT层、双GraphSAGE层、单GCN层与单GraphSAGE层相连),每个双层图神经网络与两层全连接神经网络相连,并与一层池化层相接。将节点导向任务转化为全局的图导向任务,构成 4 种不同的图卷积神经网络(GNN)模型。模型整体架构如图3。

图3 航班延误预测GNN模型结构示意

3 结果分析

基于图卷积神经网络模型验证文中方法在航班延误预测任务中的性能。电脑环境配置为Win 10(64 bit)操作系统、Intel(R) Core(TM) i5-8265U 1.60GHz处理器、16 GB 内存、4 GB 显存。利用 Python 3.7 程序设计语言,基于Pycharm的开发环境、Pytorch模型框架实现过站航班延误预测。

3.1 模型参数设定

为了使搭建的模型具有较好的性能,针对4种不同的图卷积神经网络模型,对卷积层神经元个数、全连接层神经元个数、学习率、批训练数量、迭代次数和优化器进行参数设定和比较,选取其中误差最小的参数组合,结果设定如表2。

表2 不同航班延误预测GNN模型参数设定

3.2 预测结果分析

选取平均绝对误差EMA、均方根误差ERMS和平均绝对百分误差EMAP共3 个指标以衡量各模型的预测值和真实值的距离。根据时刻数据的数据清洗标准,以 2019年数据为例,笔者将 3 476 条缺失关键数据的样本删除,最终可用延误航班样本为18 794 条。选取决策树、随机森林和 XGBoost 作为对比模型,将前 16 500 条延误航班样本作为训练集Xtrain和验证集Xval,将第16 501条～第18 794 条延误航班样本作为测试集Xtest,采用5折交叉验证的方法进行模型训练。

将测试集输入所有模型中,利用三类指标横向对比经典机器学习模型和图卷积神经网络模型的性能。7 种模型的多种预测误差如表3。经典机器学习模型的预测结果如图4～图6,图卷积神经网络模型的训练过程和预测结果如图7。为了验证模型的有效性,进一步利用2020年6月—12月内13 240 条航班中转流程中的保障节点数据建模分析,在进行数据清洗和特征转换后,比较 7 种模型的预测误差,结果如表3。

表3 不同航班延误预测模型误差

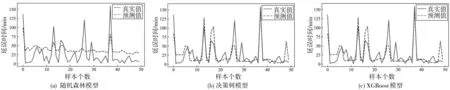
图4 模型预测结果

通过对比表3和图4、图5可知,在经典机器学习模型中,随机森林模型和决策树模型的预测各有利弊。由于随机森林模型训练了多个弱回归器,按照Bagging的规则对单棵决策树的结果进行平均,因此其偏向均值预测,对异常值的挖掘不及决策树模型敏感,而决策树模型的预测结果易呈现出高峰和低谷。总体来看,决策树模型在测试集上显示出更好的泛化能力。虽然利用经典机器学习模型能够得到相对较快的预测结果,但是笔者提出的图卷积神经网络模型的预测平均速度在实际应用场景中仍在可接受范围内。因此,从模型运算速度上来看,笔者提出的图卷积神经网络模型更实用。相对经典机器学习模型,笔者提出的 4 种图卷积神经网络模型的预测精度更高,利用图论的思想能更好地捕捉航班中转流程保障节点的时刻数据中存在的时序和时间关系。在4种图卷积神经网络中,虽然GCN模型的预测精度较差,但是其在训练时更容易稳定、快速地收敛。将GCN层-GraphSAGE集成搭建的图卷积神经网络模型预测精度在所有模型中效果最好,但是双层GraphSAGE模型在验证集上取得的精度相对GCN-GraphSAGE集成模型来说更好。综上,在过站航班保障流程提取到的时刻数据中,笔者提出的基于图卷积神经网络的航班延误预测模型预测误差更小。

图5 多种图卷积神经网络模型训练及预测结果

4 结 论

笔者使用过站航班保障流程中的时刻数据,并引入图卷积神经网络模型以提高预测精度,通过实例验证得出以下结论:

1)基于过站航班原始特征训练的对比模型预测精度较差,反映出过站航班保障流程中原始时刻特征与航班延误时间之间存在非线性或线性关系的概率较小。

2)从非延误航班中抽取各流程节点间的标准作业时段,利用其与标准时段的时间差构建的模型预测精度较好,反映出笔者提出的数据清洗方式有利于预测航班延误的发生。

3)在过站航班保障流程节点上聚合邻居节点的时间特征能够更全面的提取流程节点的时间特征,使所提出的模型在图级别的预测精度更好。

4)笔者提出的针对过站航班保障流程节点的航班延误预测方法优势在于模型的预测精度高且收敛速度在可接受范围内,但是该模型对原始数据的连贯性和逻辑性要求高,针对原始时刻数据需要进行大量逻辑判断和清洗更正工作。

尽管笔者提出的方法在短期出发延误预测方面取得了较优的结果,但在这项研究中仍然需要解决几个局限性。文中采集时刻数据人工录入方式占比较大,存在一定误差,模型的预测结果中均方根误差较大,未来针对时刻数据如何高效采集仍是需要解决的问题之一。其他相关因素也可能对起飞延误有影响,因此未来的研究仍然需要确定其他重要变量的影响,如航路的天气信息、前序机场和后序机场、其他节点的序列数据,可以进一步提高延误预测精度。笔者仅以上海浦东国际机场为例进行模型分析,来自其他机场的数据也可用于进一步调查所提出模型的稳健性和适用性。