层间连续条件对沥青路面动力特性影响的研究

高嫄嫄,焦彦鹏,王 鹏,刘 志

(1. 燕山大学 建筑工程与力学学院,河北 秦皇岛 066004; 2. 山东莱克工程设计有限公司,山东 东营 257000; 3. 天津市贰拾壹站检测技术有限公司,天津 300110)

0 引 言

沥青路面结构在车辆荷载作用下的动力特性受到结构几何尺寸、材料性能及边界条件等多因素的影响。在以往的路面结构设计中,通常将沥青路面结构简化为半空间层间连续的弹性层状体系结构[1], 但这并不符合路面结构的真实工作状态。由于沥青混合料材料的黏弹性特性,若将沥青面层简化为线弹性体对路面结构受力特性进行研究,必然会存在一定的误差。学者们已认识到这一问题并开展了相关研究工作[2-3],研究表明在沥青路面力学性能计算过程中,将沥青层视为黏弹性材料是十分必要的[4-5]。同样,由于沥青路面各结构层材料不同及施工条件和施工技术的限制,使得沥青路面结构在工作中,层间接触并不完全连续,也非完全光滑,而是介于两者之间的一种非完全连续状态[6-7]。不同层间的黏结条件对沥青路面结构力学响应的计算结果有何影响,是一个值得探讨的问题。

笔者开展了层间非完全连续沥青路面动力响应的解析求解工作。通过两类积分变换将位移控制偏微分方程组转化为常微分方程组进行求解;采用转换矩阵表征层间黏结状态,并通过传递矩阵对层状体系问题进行求解;获得考虑层间非完全连续条件的沥青路面动力响应的解析解,分析层间接触状态对路表弯沉计算结果的影响。

1 沥青层黏弹性本构模型

沥青混合料具有典型的黏弹性特性,常采用的本构模型有Maxwell模型、Kelvin模型、Burgers模型等[8]。采用修正的Burgers模型(图1[9]),其为Burgers模型的进一步改善,能更好地反映出沥青混合料永久变形的“固结效应”。图1中:σ为应力;E11、E12分别为Maxwell模型、Kelvin模型中的弹性模量;η1、η2分别为Maxwell模型、Kelvin模型中的黏性系数。

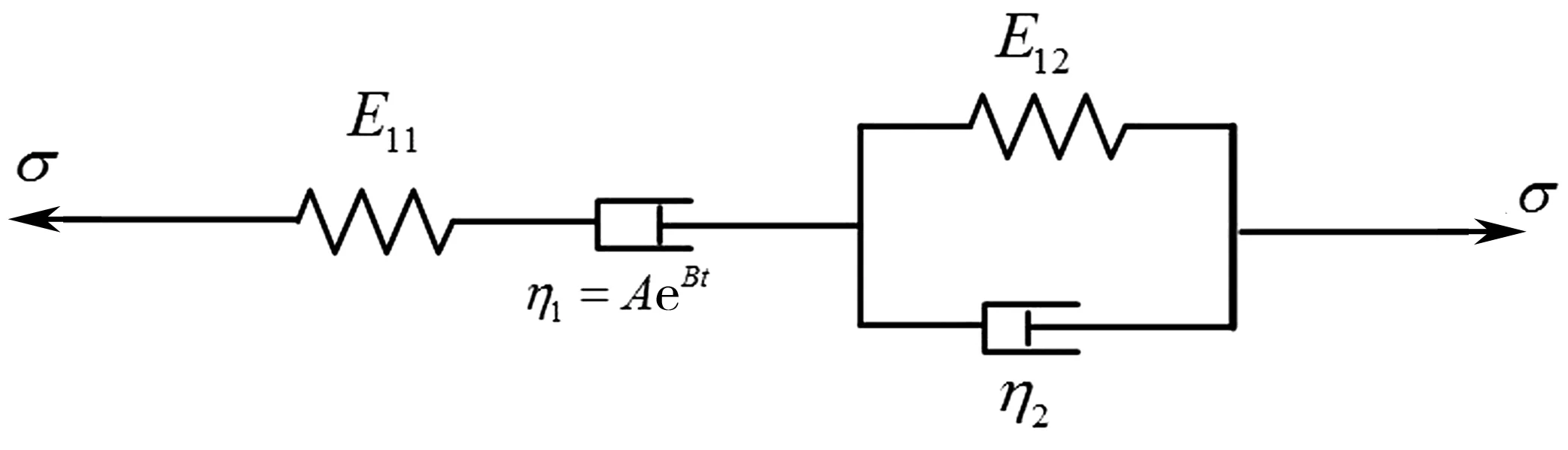
图1 修正的Burgers模型

该模型将Burgers模型中串联的外部黏壶元件变更为广义黏壶,其黏度如式(1):

η1(t)=AeBt

(1)

式中:A、B均为外部黏壶黏度系数;t为加载时间。

Burgers模型的本构方程为:

(2)

将η1=AeBt带入式(2),并对式(2)的时间变量t进行Laplace变换,可得到黏弹性算子在Laplace域的表达式:

E(s)=σ(s)/ε(s)=[sA(s+B)E11(E12+sη2)]/{sA(s+B)(E11+E12+sη2)+E11[-B2E12-s2Bη2+B3η2+s(sE11+η2)]}

(3)

式中:s为Laplace域内与时间t对应的变量。

2 传递矩阵的推导

层间非完全连续沥青路面的计算模型如图2。其中:P(t)为车辆荷载;R为荷载半径;hi为沥青路面结构第i层厚度;μi为第i层泊松比;Ei为第i层模量。

图2 多层非完全连续沥青路面模型

极坐标下动力平衡方程如式(4)、式(5):

(4)

(5)

式中:σr、σθ、σz分别为r、θ、z方向上的应力;u、w分别为水平、竖直方向的位移;τzr为剪切应力;ρ为体密度。

用位移表示应力的物理方程,如式(6)～式(9):

(6)

(7)

(8)

(9)

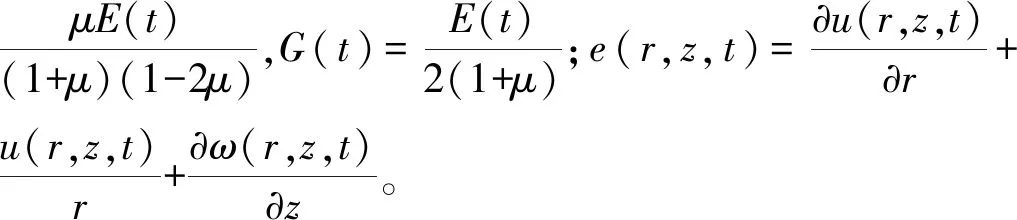
将式(6)～式(9)带入式(4)、式(5)并化简,可得由位移表示的动力平衡方程,如式(10)、式(11):

(10)

(11)

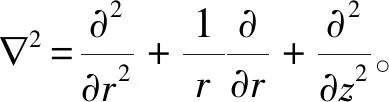
式(6)～式(11)均为关于z,r,t的偏微分方程,为便于求解,将式(8)～式(11)中的时间变量t进行Laplace积分变换并整理可得:

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

将式(16)～式(19)统一表示为矩阵形式:

(20)

由现代控制理论[10],式(20)的解可表示为:

(21)

由边界条件可确定exp[zA(ξ)]的具体表达形式,用矩阵T表示。T建立了应力与位移在各结构层间的传递关系,即为传递矩阵,如式(21):

(22)

即:

(23)

式(23)中前两个方程式可以写为:

(24)

当z=0时,由式(24)可得:

(25)

将式(25)化简并移项可得应力与位移之间的关系式:

(26)

3 层间非完全连续条件的表征

采用Goodman模型来表征层间接触状态,即层间接触条件如式(27):

τzi+1=τzi=ki(ui+1-ui)

(27)

整理可得:

(28)

式中:τzi、ui分别为第i层的底应力、位移;τzi+1,ui+1分别为第i+1层顶应力、位移;ki为层间抗剪系数。

则第i+1层顶与第i层底的应力和位移可表示为:

(29)

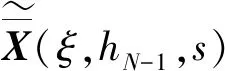
(30)

令TMc=TN-1TN-2…Ti+1TcTi…T2T1

则:

(31)

式中:TMc为前N-1层传递矩阵的累乘,可称为整体传递矩阵,仍是一个4×4的矩阵。

这样就建立了层间非完全连续沥青路面任意深度ki→∞处的状态向量与初始状态向量之间的联系。通过相应的积分逆变换和边界条件就可以得到路面结构中任意位置、任意时刻的应力与位移。

4 正确性验证

为验证笔者公式推导的正确性,采用如图2的路面结构,将修正的Burgers模型退化为Burgers模型,将层间接触条件视为完全连续,即ki→∞,采用与文献[3]相同的路面结构参数,应用前述推导公式计算路表弯沉值,并与文献[3]进行对比,如图3。

图3 与文献[3]计算结果的对比

图3中两条曲线几乎重合,可以认为笔者推导的公式正确。

5 计算实例分析

为探讨层间非完全连续条件对沥青路面路表弯沉计算结果的影响。选取典型的四层沥青路面结构(图2)。路面几何尺寸与材料参数如表1,车辆荷载为P(t)=psin2(π/Td),p=0.7 MPa。Td为荷载作用时间,Td=0.32 ms。分别考虑了层间非完全连续性条件发生路面中的不同位置及面层与基层的黏结强度因素,计算了荷载中心处路表弯沉响应,结果如图4、图5。分析了面层与基层间黏结强度与路表弯沉计算结果的关联性,如图6。

表1 沥青路面模型参数

图4 不同位置层间非完全连续的路表弯沉响应

图5 不同黏结强度的路表弯沉响应

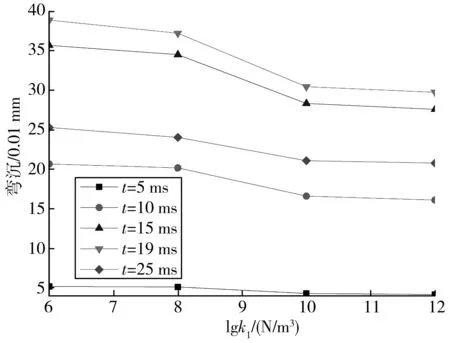
图6 弯沉随层间黏结强度变化对比计算结果

图4为沥青路面中不同位置处存在层间非完全连续情况时的路表弯沉的计算结果。工况1～工况4分别为路面各结构层层间完全连续、面层与基层、基层与底基层和底基层与土基的层间非完全连续并且ki=109N/m3。由图4可知:工况2～工况4对沥青路面路表弯沉的影响程度依次降低,状况2(面层与基层非完全连续)对沥青路面路表弯沉的影响最大,弯沉峰值为36,相比层间连续状态,弯沉峰值升高了12.4%;工况4(底基层与土基非完全连续)对沥青路面路表弯沉的影响最小,弯沉峰值为30,基本接近层间完全连续状态(29.9)。

面层与基层间的层间黏结强度对路表弯沉的影响最大。由图5可知:当层间黏结强度大于k1=1012N/m3时,路表弯沉峰值为29.9(0.01 mm),弯沉响应曲线接近于层间完全连续状态;当层间黏结强度逐渐减小时,任意时刻的路表弯沉响应均不断增大,所以在路面结构设计时应对面层与基层的黏结强度加以考虑。

由图6可知:不同时刻弯沉值随面-基层黏结强度的变化有相同的变化趋势,弯沉值w都随k1的增加而减小,并且k1在108～1010N/m3范围内时这种变化趋势最为明显。这也说明k1为108～1010N/m3时,对弯沉的计算结果影响最显著,再次证明在此区间是不能将层间黏结条件简单的视为完全滑移或者完全连续的状态。

6 结 论

从动态平衡方程出发,结合坐标变换,考虑路面结构层间结合条件,推导了车辆荷载作用下层间非完全连续沥青路面动力响应。通过实例计算,分析非完全连续层间条件出现的位置及层间黏结强度对沥青路面路表弯沉响应的影响。通过实例计算分析可知:

面-基层的层间黏结状态对路表弯沉响应的影响最大;实例中当k1=108～1010N/m3时,其对弯沉计算结果的影响最为显著;面-基层间黏结强度的增加可减低路表弯沉。在路面施工过程中不能实现面-基层间的完全连续,但可尽量是层间的黏结强度控制在一个合理的范围,提升路面服务能力,延长路面使用寿命。