跨座式单轨智能编组固定时间协同控制研究
刘朝涛,刘浩鸣,杜子学,邬浩鑫 ,侯忠伟
(1. 重庆交通大学 机电与车辆工程学院,重庆 400074; 2. 重庆交通大学 交通运输学院,重庆 400074)
0 引 言
随着城市化进程加速,中小城市交通拥堵现象日益凸显,亟需大力发展建设成本低的除地铁制式之外的新型城市轨道交通系统。跨座式单轨交通相较地铁交通具有成本低、噪音低、转弯半径小等优点,是中小城市轨道交通建设的重要选择。重庆轨道交通二、三号线是我国目前唯一成功运营的中大运量跨座式单轨交通线路。重庆单轨运营实践发现,现行跨座式单轨列车是以固定时间间隔和固定物理联挂的多编组方式运行,而实际每天早中晚客流分布波动较大,造成了很大的运力浪费和车辆资源(车辆配置数多)浪费,存在运营投入大的问题。尤其是新冠疫情严重时,八编组列车竟然出现每车仅有3~4位乘客的情况。亟需开展跨座式单轨智能编组相关理论、方法和技术研究来适应客流波动大的场景需求,同时解决轨道交通投入大和运营成本高的问题。
围绕跨座式单轨智能编组协同控制问题,基于分布式协同控制的思想,借鉴分布式控制方法在智能网联道路车辆以及高铁列车、多智能体协同控制中的相关成果[1-4],结合跨座式单轨的运行特点以及滑模变结构控制的强鲁棒性、响应快速实时性好的特点,建立跨座式单轨智能编组(straddle monorail intelligent marshalling, SMIM)动力学模型,构建了分布式固定时间滑模协同控制架构;提出了SMIM分布式固定时间滑模协同控制(DFTSMC)方法,应用了分布式固定时间滑模估计器(DFTSME),为SMIM队列中每个编组车辆分别设计了分布式固定时间积分滑模控制器(DFTISMC),并通过数值仿真验证了所提出的控制方法的有效性。
1 跨座式单轨智能编组动力学模型
跨座式单轨智能编组动力学模型是协同控制方法研究的基础。本研究基于质点模型的指导思想和列车牵引动力学理论,进行了SMIM运行受力分析。SMIM单车行驶时受3个力作用,分别是牵引/制动力、基本运行阻力和额外运行阻力,它们之间的关系可以用式(1)来描述:
ma=u-f1(v,t)-f2(p,v,t)
(1)
式中:m为SMIM单车的质量;a为加速度;u为牵引/制动力;f1(v,t)为基本运行阻力;f2(p,v,t)为附加运行阻力;v为速度;p为位置。
基本运行阻力f1(v,t)一般由如下形式,见式(2)的戴维斯[5]方程描述:
f1(v,t)=α+βv+γv2
(2)
式中:α、β、γ均为经验系数,在这里不做过多的讨论,假定是已知的;f2(p,v,t)作为附加运行阻力,包括曲线阻力,坡道阻力,隧道阻力以及其他一些因素导致的阻力。通常按经验公式计算,在这里假定是已知的。
取如下状态变量:
(3)
综合式(1)~式(3),可以得到如下方程:
(4)
式(4)是SMIM单车的动力学模型,对于SMIM编组,假设编组是由n个单车组成(n∈R且为正整数),那么可以有方程为:
(5)
式中:i为SMIM编组里的第i辆车,i∈(1,2,3,…,n);xi1为第i辆车的位置;xi2为第i辆车的速度;mi为第i辆车的质量;fi2(xi1,xi2,t)为第i辆车的附加运行阻力。
2 跨座式单轨智能编组分布式固定时间滑模协同控制
分布式控制方式具有高扩展性、高灵活性等优点,分布式控制是近几年国内外研究的热点之一。V.ANDRIEU等[6]最早提出了固定时间稳定的概念,A.POLYAKOV[7]后来提出了固定时间Lyapunov稳定理论,为后续的固定时间控制算法的设计奠定了基础。
2.1 分布式固定时间滑膜协同控制架构
SMIM整个行驶过程包括出站、加速、惰性、减速、进站,在行驶全过程中,需要达到的控制目标是:
1)领航车辆:能够在短时间内准确的跟踪控制中心、云平台或预设的速度-距离曲线。
2)编组内非领航车辆:能够在短时间内准确的跟踪领航车辆速度并保持一致,保持期望的车间间距dei。
为达到以上的目标,我们设计了SMIM分布式固定时间滑模协同控制架构(图1),设计了位置和速度双闭环控制提高了系统的可控性。

图1 分布式固定时间滑模协同控制架构
每个编组之间可以无线通讯(通讯可以采取5G、Wifi或者其他组合方式等)来实时交换彼此的信息,受限于车间间距以及路况,我们采取邻接通讯的方式,如图1可见,每个编组可以和其前后相邻的编组通讯交换彼此信息。
对于领航车辆,控制中心、云平台或预设的速度-距离曲线指令送达给DFTISMC 1,其直接控制领航车辆,通过选取适当的控制器参数,领航车辆可以独立于初始状态在固定时间内(根据调整控制参数来控制固定时间的大小)准确跟踪控制中心、云平台或预设的速度-距离曲线下发的指令,极大地提高了工程实用性,减少了跟踪时间,提高了运行效率。
对于编组内非领航车辆,首先由DFTSME估计出领航车辆的速度和位置状态,再将指令发送给DFTISMC 2,通过选取适当的估计器参数和控制器参数,编组内非领航车辆可以独立于初始状态的估计出领航车辆的速度状态和位置状态,并在固定时间内(根据调整控制参数来控制固定时间的大小)准确跟踪领航车辆的速度且保持编组之间期望的车间间距dei,提高了工程实用性。
2.2 分布式固定时间滑模估计器设计
为方便估计器和后面控制器的设计,先给出如下定义:
定义1假设非线系统式(5) 为全局渐近稳定, 若存在有限收敛时间Ts(x0),对于所有的t≥Ts满足x(t)=0恒成立,则系统式(5)为全局有限时间稳定[8]。
定义2若系统式(5)为全局有限时间稳定,同时收敛时间存在确定上界且上界值与系统状态变量无关,则称系统式(5)为全局固定时间稳定[7]。
由前面控制架构可以得知,SMIM非领航车辆需要先对领航车辆的速度状态进行估计,再将估计指令发送给DFTISMC 2进而控制车辆。
为了方便DFTSME的设计,我们利用代数图论来描述车辆间的通讯拓扑关系。
在由N个SMIM组成的编队系统中,如果第j个编队成员Oj可以接收到第i个编队成员Oi的信息,第i个编队成员Oi也可以接收到第j个编队成员Oj的信息,由SMIM组成的图G为无向图,图G中就有一条边从Oj指向Oi(也可以说有一条边从Oi指向Oj),记为(Oj,Oi)∈φ⟺(Oi,Oj)∈φ,在编组中,领航车辆只能接收第2个编组的信息,编组中的尾车只能接收前车的信息,其余编组车辆皆可以接收前车和后车的信息,故图G的加权邻接矩阵为:
(6)
图G的入度矩阵D=diag(d1,…,dN),对角元素为:
(7)
那么图G对应的拉普拉斯矩阵:
L=D-A
(8)
图G对应的领航邻接矩阵B:
B=diag(b1,b2,…,bN)
(9)
当第i个编队成员Zi可以接收到领航者的信号时,bi=1,否则bi=0。
定义矩阵Q:
Q=L+B
(10)
另外,为了方便给出DFTSME,我们做出以下符合SMIM运行实况的假设:

根据文献[9]中的DFTSME,并结合SMIM的通讯拓扑结构,DFTSME可设计如下:
(11)
(12)
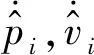
先给出以下引理:
引理2[11]如果ξ1,ξ2,…,ξN≥0,那么有下述结论成立:
(13)
(14)

(15)
定理1中位置估计的证明和速度估计的证明过程类似,在此仅对位置估计器进行证明。
(16)
将式(16)增广并引入克罗克内积后可得:
(17)
其中:YN=[1]N,I3是三阶单位矩阵。
由引理1可知Q⊗I3是正定的。选取Lyapunov函数为:
皖河流域下游属平原圩区,地势低平,水系复杂,河床落差小、弯道多,水流缓慢,泄洪能力差,多涝灾有必然性。皖河流域下游千亩以上重点圩口104个,总面积880.69 km2,耕地5.33万公顷,其中万公顷以上圩口22个。建国以来60余年间,就发生过较大洪涝灾害17次,平均不到3年一次,与上游洪水出现保持高度一致。涝灾严重的是皖河中下游支流及武昌湖周边圩区。
(18)
为了简化表达,令δ=(Q⊗I3)ep,则有:
(19)
根据定理2可得:
(20)

证毕。
2.3 分布式固定时间积分滑模控制器设计
由前面控制架构可以得知,SMIM领航车辆得到云平台、控制中心或预设速度-曲线指令后由DFTISMC 1控制车辆;非领航车辆由DFTSME给DFTISMC 2发送指令进而控制非领航车辆。
2.3.1 固定时间积分滑模控制器1的设计
为了方便DFTISMC 1的设计,先给出如下引理。
引理3如果存在一个连续径向无界函数V:Rn→R+∪{0}满足:
V*(x)≤k3Vz(x)-k4Vg(x)
(21)
式中:k3,k4>0,z>1,0 (22) 对于领航SMIM车辆,给出如下定义: (23) 式中:e1p为领航SMIM车辆位置误差;p1为领航车辆位置;pr为领航车辆位置指令;e1v为领航车辆速度误差;v1为领航车辆速度;vr为领航车辆速度指令。为了收敛的快速性和平滑性,采用如下的积分滑模面: (24) 对式(24)求导可得: (25) 当系统到达滑模面时,有: (26) 则可以得到: (27) 领航车辆固定时间积分滑模控制器设计为: (28) 2.3.2 固定时间积分滑模控制器2的设计 为了方便DFTISMC 2的设计,先给出如下定义,对于编组内的非领航SMIM车辆: (29) 式中:eip为编组内非领航SMIM车辆位置误差;pi和pi-1分别为编组内第i辆和第i-1辆SMIM车辆位置;eiv是第i辆SMIM车辆估计速度和领航车辆速度的误差。为了收敛的快速性和平滑性,采用如下的积分滑模面: (30) 对式(30)其求导得到: (31) 非领航车辆固定时间积分滑模控制器设计为: (32) 定理2对于系统式(5)的SMIM领航车辆,当选用滑模面式(24)及控制器式(28)时,系统为全局稳定且满足SMIM领航车辆位置误差e1p和速度误差e1v于固定时间TP收敛至零, 其中TP满足下面不等式: TP≤T1+T2 (33) 即领航车辆在固定时间TP内跟踪到位置指令和速度指令。 对于系统式(5)的SMIM非领航车辆,当选用滑模面式(30)及控制器式(32)时,系统为全局稳定且满足车辆位置误差eip和速度误差eiv于固定时间TC收敛至零, 即在TC时间内,编组非领航车辆的速度跟踪上领航车辆的速度并且保持理想的车间间距dei,其中TC满足下面不等式: TC≤T0+T1+T2 (34) 定理2中两个控制器的证明过程类似,在此仅证明控制器1。 证明:选取以下Lyapunov函数: V2=|e1p| (35) (36) 根据引理3可以知道滑模运动阶段的收敛时间T1满足: (37) 另外,再选取以下Lyapunov函数: V3=|s1| (38) (39) 根据引理3可以知道趋近阶段的收敛时间T2满足: (40) 证毕。 因此可以得出结论, 通过适当地选择参数, 可以使SMIM领航车辆的状态在固定时间TP内跟踪上控制中心、云平台或预设的速度-距离曲线。对于SMIM中非领航车辆,根据2.2节结论,DFTSME在T0内估计出领航车辆的位置和速度,再根据本节结论,可以得知编组中非领航车辆在TC时间内跟踪上预期的速度-距离曲线,在此不再赘述。 为了验证SMIM分布式固定时间滑模协同控制方法,本研究仿真对象为车辆质量作了比例缩小的跨座式单轨智能四编组车辆。缩小质量是为了节约仿真时间,但不影响控制算法有效性验证的结果。有效性验证中是将文献[13]有限时间滑模控制算法作为对比分析的对象。 SMIM单车主要仿真参数设置是: 1)领航车辆:m1=1 200 kg, 初始位置为30 m,初始速度为-15 m/s;控制器参数:γ1=0.3,z1=19,n1=17,δ1=0.3,r1=3,q1=5,γ2=10,z2=3,n2=1,β2=10,g2=5,q2=7。 2)第1辆跟随车:m2=1 300 kg,初始位置为70 m,初始速度为-10 m/s,与前车理想跟车间距40 m;控制器参数:γ1=0.25,z1=19,n1=17,δ1=0.25,r1=3,q1=5,γ2=5,z2=3,n2=1,β2=5,g2=5,q2=7。 3)由于篇幅限制,第3和第4辆跟随车辆主要仿真参数不再赘述。 DFTSME参数设置如下: 编组中每辆车的基本运行阻力f1和附加运行阻力f2均假定为经验常数。 图2分别为SMIM在加速-巡航行驶时控制算法控制SMIM车辆和有限时间控制器控制SMIM车辆的位置和速度的追踪图,其中由于速度的目标速度指令是相同的,分开表示更能清楚的做出对比,4辆车的速度追踪分别如图2。4辆SMIM车均是不同的质量,不同的初始位置和速度,可以看出,领航车辆用笔者所设计算法时,在11.5 s时位置和速度均跟踪到指令曲线,而有限时间控制器在17.0 s时位置和速度才跟踪上指令曲线;第1辆跟随车用笔者所设计算法时,在13.0 s时既速度跟踪到领航车辆速度,位置上也和领航车辆保持了设定的间距,而有限时间控制器在26.0 s时才达到同样的要求;第2辆跟随车用笔者所设计算法时,在12.0 s时既速度跟踪到领航车辆速度,位置上也和第1辆跟随车保持了设定的间距,而有限时间控制器在18.0 s时才达到同样的要求;第3辆跟随车用笔者所设计算法时,在14.0 s时既速度跟踪到领航车辆速度,位置上也和第2辆跟随车保持了设定的间距,而有限时间控制器在28.0 s时才达到同样的要求。可以看出笔者所设计布式固定时间协同控制算法能使编组内领航车辆在较短时间内跟踪到指令曲线;编组内非领航车辆在较短时间内跟踪上领航车辆的速度并且和前车保持设定的间距。 图2 跨座式单轨智能编组控制算法对比 系统性的提出了跨座式单轨智能编组分布式固定时间滑模协同控制方法,该方法包括了领航车辆的固定时间积分滑模控制器、非领航车辆的固定时间滑模估计器以及固定时间积分滑模控制器;同时,对分布式固定时间滑模控制算法的有效性进行了仿真分析,数值仿真结果显示该控制算法可以使跨座式单轨智能编组中的车辆分别在11.5、13.0、12.0、14.0 s跟踪上目标的速度-距离曲线,而基于有限时间控制器分别在17、26、18、28 s跟踪上目标的速度-距离曲线,仿真结果表明分布式固定时间滑模协同控制算法有效且能减少跟踪时间。提出的分布式固定时间滑模协同控制方法对跨座式单轨智能编组协同控制具有理论和应用参考价值。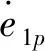

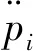


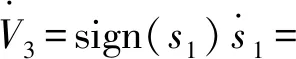
3 仿真实验

4 结 语

