三维方腔内导电流体第1次Hopf分叉

张敬奎，常家鹏，崔苗，李琦芬，任洪波，杨涌文

1.上海电力大学 能源与机械工程学院，上海 200090

2.大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室，大连 116024

近年来，在天体物理、热核聚变、磁流体推进、电磁冶金、磁流体发电等领域中，磁流体动力学（Magnetohydrodynamics， MHD）理论获得发展和应用，其中流动转捩问题受到广泛关注和研究。自1883年雷诺［1］在著名的圆管流动实验中发现流体存在截然不同的流动状态开始，流体流动转捩问题［2-3］便成为了流体力学研究的焦点问题。外加磁场作用下导电磁流体转捩引起的流动不稳定性，由于受多物理场耦合影响，更成为流体力学研究的难点。本文选取三维腔体内磁流体Hopf分叉引起的不稳定转变开展研究。

在工程和自然领域，普遍存在非线性系统参数演化产生的自激振荡，振荡平衡点的失稳则可能引起Hopf分叉。Hopf分叉理论在工程中具有重要应用，例如，在航空航天领域，Hopf分叉临界参数被用于预测超声速飞行器壁板发生振颤的临界速度和振颤频率；在流体机械领域，Hopf分叉理论被应用于压气机旋转失速平衡点的判断。在雷诺数Re较低的情况下，流体保持稳态层流的流动状态。增加Re至某一临界值，稳态的流动转变为非稳态周期性振荡流动，称为第1次Hopf分叉（the first Hopf bifurcation）。继续增加Re至另一临界值，使得非稳态周期性振荡流动转变为非稳态准周期性振荡流动，称为第2次Hopf分叉（the second Hopf bifurcation）。再继续增加至某一更高的临界值，非稳态准周期性振荡流动将转变为湍流，称为第3次Hopf分叉（the third Hopf bifurcation）。本文选取三维腔体内导电流体由稳态流动转变为非稳态周期性振荡流动的不稳定转变开展研究。这种不稳定转变已在多项数值研究和实验研究工作中（例如文献［4-5］）观察到，是由次临界状态下的第1次Hopf分叉引起，具有唯一主导的振荡频率。

近年来，众多研究者对第1次Hopf分叉引起的不稳定转变开展了大量研究工作。大部分研究工作针对二维腔体内流体流动的不稳定性转变，例如文献［6-17］。这些研究工作主要采用了线性稳定性分析方法，获得了二维方腔内第1次Hopf分叉失稳对应的临界雷诺数Recr（范围为7 402～10 500）和临界无量纲角频率（范围为0.439 9～0.61）。尽管从第1篇预测二维腔体内第1次Hopf分叉临界参数的研究工作［18］至今，已持续30年，但如上述数据，临界雷诺数和临界振荡频率的预测结果仍具有很大分歧。近十多年，也有研究者开始针对三维腔体内流体第1次Hopf分叉的不稳定转变开展研究。相对二维流动Hopf分叉不稳定性的研究，三维流场下采用广泛使用的线性稳定性分析方法难于求解特征值方程，而采用直接数值求解则需要大量的网格节点和计算时长。因此，三维腔体内Hopf分叉流动的研究结果也相对较少。

表1总结了三维方腔内流体流动第1次Hopf分叉的临界参数预测结果。从表中可以看到，现有研究获得的三维流动第1次Hopf分叉失稳的临界雷诺数范围为1 700～2 250，对应的临界无量纲角频率范围为0.472～0.651。文献［4-5，19-21］给出了具体的临界参数预测结果，结果差异不大。而文献［22-24］则给出了较大差异的临界参数预测范围。二维和三维流动第1次Hopf分叉失稳对应的临界雷诺数存在更大的差异。这是由于展向壁面边界条件的影响，并且腔体内第1次Hopf分叉失稳对应的临界雷诺数与展向尺寸的长度呈负相关［24-25］。这也意味着，展向尺寸和展向壁面边界强化了三维腔体内流体流动的稳定性。

表1 三维方腔内由第1次Hopf分叉的临界参数预测结果Table 1 Prediction of critical parameters by the first Hopf bifurcation in a three-dimensional square cavity

从当前国内外的研究工作中可以看到，研究者对二维和三维腔体内流体第1次Hopf分叉失稳的研究工作还不完善。由于采用的方法不同，不同研究者所预测的流动状态发生转变的临界参数还没有取得一致的结果。而针对磁场作用下导电流体第1次Hopf分叉失稳引起的流动不稳定性，目前还未有研究工作涉及。磁场作用下腔体内导电流体由次临界流动状态下的准稳态流动转变为周期性非稳态振荡流动状态的速度、振幅和频率演化特性有待揭示。本文采用自己开发的配置点谱方法（Spectral Collocation Method，SCM）和人工压缩法（Artificial Compressibility Method，ACM）相结合的高精度数值方法SCM-ACM［26-27］，直接求解三维流动控制方程，精确捕捉次临界流动状态下的速度演化过程，研究一定磁场强度对振幅衰减和振荡频率的影响规律，预测一定哈特曼数Ha条件下第1次Hopf分叉失稳的临界雷诺数，采用Fourier分析法获得临界无量纲角频率，运用Richardson拓展法提升临界参数预测的准确度。

1 数学方程

1.1 人工压缩格式的控制方程

本文同样选取表1中研究者所采用的三维方腔顶盖驱动流为对象，分析磁场作用下三维腔体内导电流体流动的第1次Hopf分叉失稳。如图1所示，三维方腔的边长为L，针对次临界流动状态下导电流体的三维流动，在X轴方向施加一定的磁场。引入人工压缩法后的流动控制方程如式（1）和式（2）所示。人工压缩法由Chorin［28］首次提出，适用于稳态和非稳态的不可压缩或弱可压缩流体流动的求解，具有形式简单、易于实施和收敛的特点。

式中：p为压力；u为速度矢量；ρ为流体密度；v为运动黏度；c为人工压缩因子；t为伪时间变量；J为电流密度，J=ε(u×B)，其中ε为电导率；B为磁场。

采用式（3）的变换，对式（1）和式（2）进行无量纲化处理，获得如下形式的无量纲化控制方程：

式中：Re为雷诺数；Ha为哈特曼数；U0为顶盖移动速度；μ为动力黏度；B0为X轴方向施加的磁场；物 理 区 域 为Ω={E：(X，Y，Z)∈[0，1]×[0，1]×[0，1]}，这里E表示区域。

1.2 边界条件和初始条件

三维方腔各壁面均设置无滑移边界条件，顶部以恒定速度沿X轴方向移动，无量纲速度为1。为了获得次临界流动状态下的准稳态结果，合适的初始条件对快速获得准稳态结果至关重要。在低雷诺数条件下，例如当Re=100时，除边界条件外的速度和压力初始值均给定0，即可以快速获得三维稳态流动的结果。然而，当Re增至次临界流动状态时，这种初始条件很难在短时间内计算获得准稳态的结果，相关研究和分析参见文献［21］。本研究通过逐次增加Re的方法，以前次Re条件下的速度和压力结果作为增大Re后的初始条件，从而可以快速获得次临流动状态的数值结果。

2 数值方法

2.1 空间离散方法

本文采用配置点谱方法SCM对人工压缩格式的控制方程进行离散化处理。这种方法于1944被提出，从20世纪90年代开始逐渐进入主流的科学计算方法序列，目前已广泛应用于流体力学、传热学、电磁学等领域的数值求解，并被证明具有高精度和指数收敛的特性。作者已采用SCM与ACM相结合，开发了直角坐标和柱坐标系统下求解不可压缩流动问题的数值方法SCMACM［26-27］，并检验了其求解二维和三维流动问题的精确性和收敛特性。采用SCM离散控制方程的主要过程如下：

选用切比雪夫-高斯-洛巴托配置点（Chebyshev-Gauss-Lobatto， CGL）［29］，计算所有配置点N中第i配置点ri的位置，以X方向为例，配置点位置如式（9）所示。配置点在标准谱空间取值，因此 需 要 将 实 际 物 理 区 域{E：(X)∈[Xmin，Xmax]}转 化 为 谱 空 间 区 域{E：(r)∈[-1，1]}，如式（10），则空间偏微分项可转化为式（11）所示的形式。

通用变量φ(r)可以通过所有配置点的级数进行近似，即

式中：h(r)为拉格朗日插值多项式，即

式中：T′N(r)为切比雪夫多项式TN(r)的一阶偏导数。TN(r)=cos(icos-1(r))，i=0，1， …，N。

因此，可以获得变量φ(r)在r=r0处的一阶和二阶偏导数，即

式中：D(1)和D(2)为CGL配置点的一阶和二阶系数矩阵，其表达式为

在获得空间偏导数的系数矩阵后，即可整理出无量纲控制方程（4）～（7）的空间离散式，即

式中：A、B和C为X、Y和Z方向配置点Nx、Ny和Nz所对应的一阶系数矩阵D(1)；E、F和M为X、Y和Z方向配置点所对应的二阶系数矩阵D(2)。

2.2 时间离散方法

在时间离散处理上，本文选用四阶龙格库塔方法，这种处理方法对不稳定的流动求解具有很好的适用性，由于论文篇幅限制，相关离散处理可参见文献［26-27］。

3 结果与分析

3.1 有效性验证

为了检验数值结果的有效性，本文分别选取了方腔顶盖驱动流的数值模拟结果和实验结果进行验证，如图2所示。在Re=1 000和Re=1 480的层流状态下，本文计算结果与数值模拟结果都吻合良好。图2（a）中的数值研究工作［30-33］均采用了高精度的数值方法，可以作为基准解进行验证。图2（b）为本文计算结果与Liberzon等［22］开展的数值模拟和实验研究结果的对比验证。Liberzon等开展了极少被开展的方腔顶盖驱动流实验研究，他们分别以水和甘油为介质，采用粒子图像测速仪（PIV）测量了流体速度分布。本文结果与Liberzon等的数值模拟结果吻合良好，而与他们的实验结果相比却略有差异，这是由于实验边界条件的设置、测量误差、振动和噪声等因素所致。值得说明的是，在2种Re条件下本文仅用了363的节点数目，远少于其他数值模拟所采用的网格数目。

3.2 磁场对速度演化的影响

在次临界流动状态下，依次计算了不同雷诺数和磁场条件下的速度演化。三维流场中，不同节点具有不同的速度和振荡幅度，但具有相同的振荡频率和振幅衰减速率。为了准确捕捉速度振荡的演化过程和精确计算速度振幅的衰减，本文选取速度振幅最大区域的节点反映速度场振荡信号的变化。这种选取一个节点的速度来反映速度场振荡变化的方法也在其他研究工作中被采用，例如文献［4-5，22］等。速度U的振幅最大，因此，所有计算工况均选择U振幅最大区域的节点（0.33，0.328，0.5）作为监测点。Ha=0时选取点速度U在Re分别1 900、1 910、1 915和1 920的时间演化如图3所示。在次临界流动状态下，速度随着时间的增加周期性振荡，且振幅逐渐衰减。当计算时间无限长时，速度将趋于稳态。同时可以看到，随着Re的增加衰减速率逐渐减小，可以预见，当Re增加至某一临界值时，速度随着时间周期性振荡的衰减速率将减小为0，此时腔体内流动状态由三维稳态流动转变为非稳态周期性振荡流动，即发生第1次Hopf分叉。然而，通过直接模拟获得第1次Hopf分叉的临界雷诺数是难以实现的，目前国内外的研究多以振荡衰减速率的变化预测发生第1次Hopf分叉的临界雷诺数。

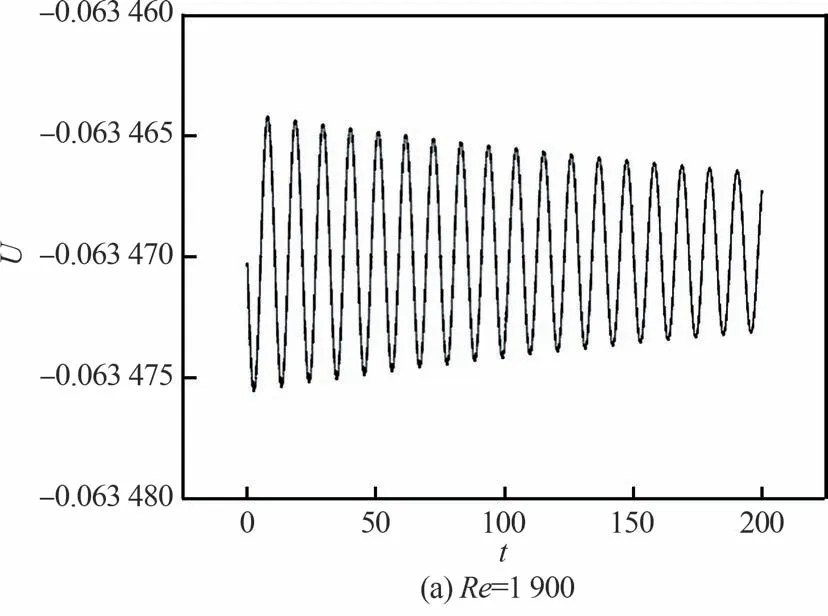
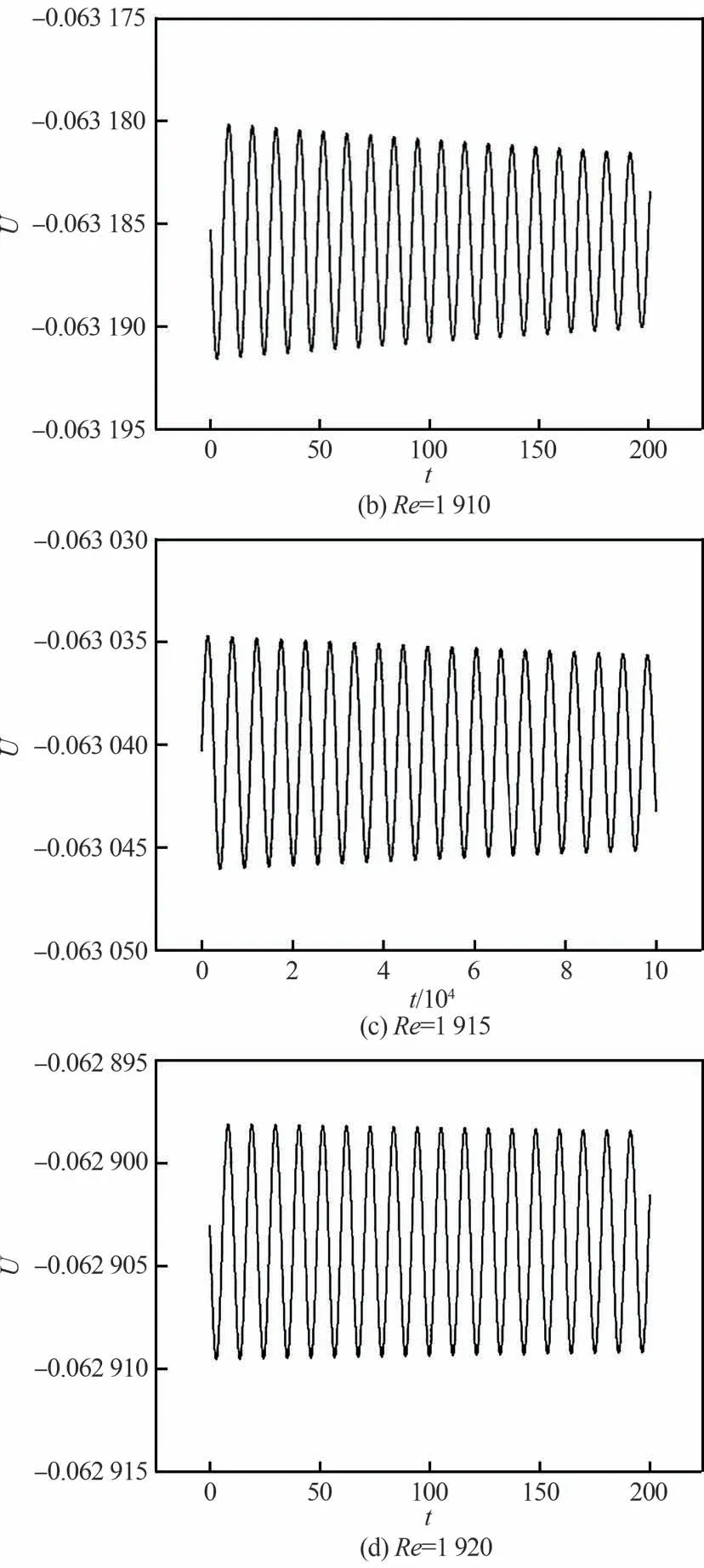
图3 Ha=0选取点速度U的时间演化Fig.3 Time evolution of velocity U for selected point with Ha=0

选取Re=1 920的次临界流动，在一定范围内增加Ha（0～5），研究磁场对次临界振荡流动特性的影响。选取点速度U在Ha分别为0、1、2和5的时间演化如图4所示。在次临界流动状态下，速度U振荡流动的衰减速度对Ha小范围内的变化响应迅速。随着Ha的增加，速度U振荡的衰减加快，振荡流动趋于更加稳定，从而使得发生第1次Hopf分叉的临界雷诺数增加。此外，每个Re条件下，趋于稳态的平均速度U（绝对值）随Ha的增加而显著增加。这是由于磁场强度的增加抑制了主旋涡的流动强度，并使主旋涡中心发生位移，引起该点X方向速度U与速度矢量夹角减小所致。

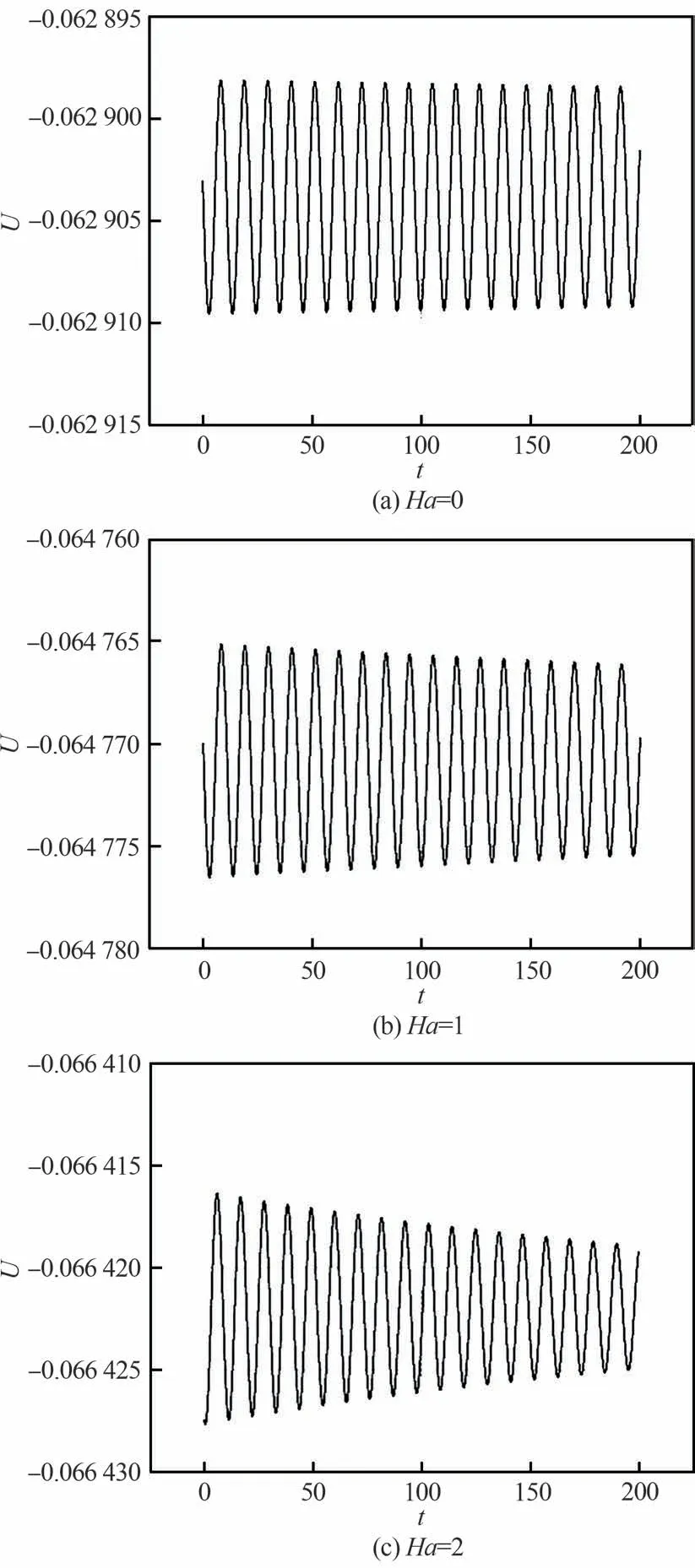
图4 Re=1 920时不同Ha条件下选取点速度U的时间演化Fig.4 Time evolution of velocity U for selected point for different Ha with Re=1 920

3.3 磁场对振幅衰减速率的影响

提取图4中所有速度振荡的振幅，在时间轴上的分布如图5所示。极小的振幅随时间呈指数形式衰减。次临界流动状态下的震荡信号可以通过振幅随时间变化的拟合函数描述，如式（22）所示。实部σ表示振幅的增长速率，可以通过式（23）计算获得。σ＜0时对应次临界流动状态，σ=0时为第1次Hopf分叉发生的临界状态，而当σ＞0时为超临界流动。虚部ω表示振荡频率，本文通过Fourier分析将时域振荡信号转化为频域振荡信号。

图5 Re=1 920时不同Ha条件下选取点速度U的振幅演化Fig.5 Amplitude evolution of velocity U for selected point for different Ha with Re=1 920

图5中可以看到，Re=1 920时不同Ha条件下，最大速度振幅（Ua）的衰减速率均为负值，为次临界流动状态下的结果。随着Ha的增加，速度振幅的衰减速率急剧增加。Ha从0增加至5时，振幅衰减速率的绝对值从3.16×10-4快速增加至1.66×10-2。相同Re下，速度振幅衰减速率的绝对值随Ha在一定范围的增加呈严格抛物线形式增加，如图6所示。磁场强度显著抑制了次临界流动状态的速度振荡，使振幅急速减小，流动更快地趋向稳态流动。从而引起发生第1次Hopf分叉的临界雷诺数随Ha的增加而显著增加。

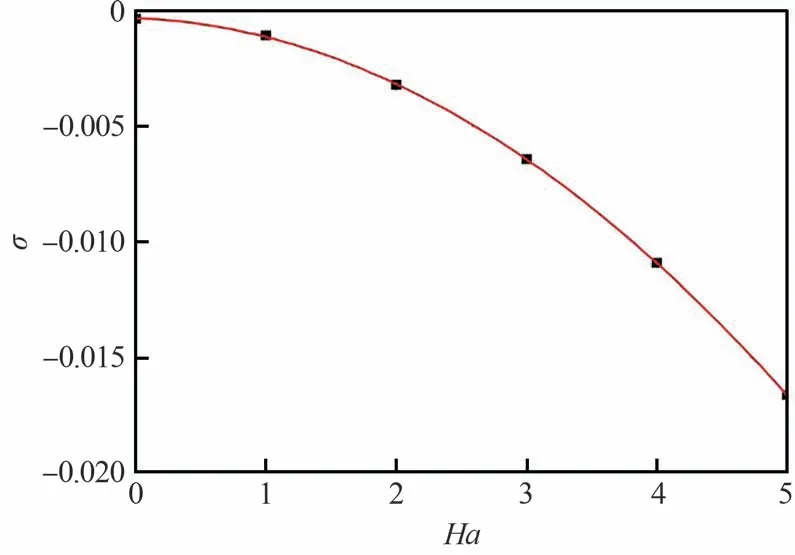
图6 Re=1 920时不同Ha条件下速度振幅的衰减速率Fig.6 Decay rate of velocity amplitude for different Ha with Re=1 920

3.4 磁场对无量纲角频率和临界雷诺数的影响

采用Fourier分析方法获得的速度振幅频域分布如图7所示。在所有Ha参数下，速度振荡均仅有唯一主导的无量纲角频率，验证了流动由稳态转变为非稳态周期性振荡流动是由Hopf分叉所引起。尽管磁场对速度振荡具有显著的抑制作用，然后一定范围的磁场变化（Ha=0～5）对主导无量纲角频率却无影响，仅使主导角频率所对应的速度振幅有所减小。最大振幅对应的无量纲角频率均为0.575 2，与无磁场作用下的角频率完全相同。

图7 Re=1 920时不同Ha条件下速度振幅的频域分布Fig.7 Frequency distribution of velocity amplitude for different Ha with Re=1 920

不同Ha参数条件，分别逐次增加Re，对次临界流动状态下的流动工况进行计算，获得不同Re下速度振荡的衰减速率（Ha=1），如图8所示。衰减速率的绝对值随Re的增加呈严格线性减小趋势。绘制不同Re下衰减速率的曲线，即可获得衰减速率为0时发生第1次Hopf分叉的临界雷诺数Recr。采用Richardson拓展方法对不同Ha参数下的Recr进行改进，以获得更为精准的Recr，实施过程参见文献［4，21］。图9给出了一定Ha范围内（Ha=0～5）发生第1次Hopf分叉的Richardson拓展方法改进后的Recr。无磁场作用下，发生第1次Hopf分叉的Recr已在表1中获得验证，其中文献［21］中的结果即为本文无磁场作用下的Recr。随着Ha的增加，Recr显著增加，且呈抛物线增加趋势。这源于速度振荡衰减速率的绝对值随Ha的增加呈抛物线形式增加。随Ha从0增加至5，Recr从1 916.6以抛物线形式增加至2 040.1。

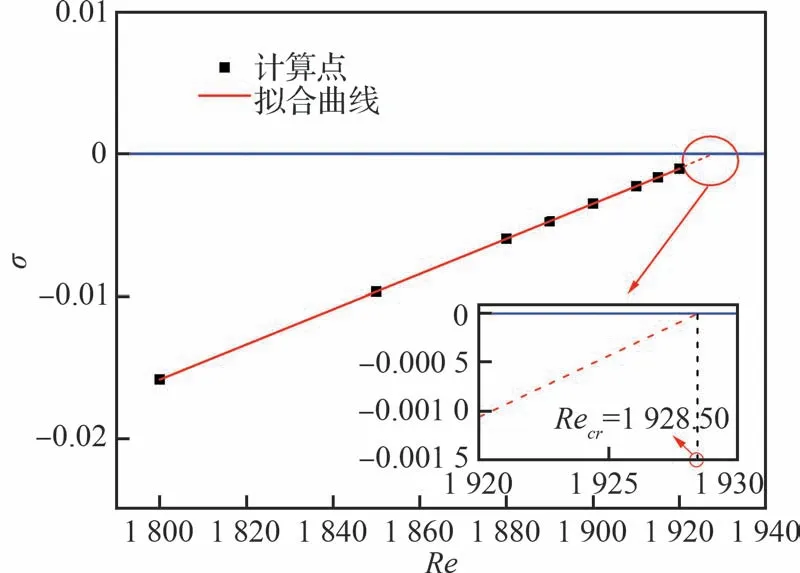
图8 Ha=1时不同Re条件下速度振荡的衰减速率σ及临界雷诺数Recr预测Fig.8 Decay rate of velocity oscillation for different Re with Ha=1， and prediction of critical Reynolds number Recr

图9 不同Ha条件下的临界雷诺数RecrFig.9 Critical Reynolds number Recr for different Ha

4 结 论

本文采用课题组开发的高精度数值方法SCM-ACM，通过逐次增加Re并更新初始条件的方法，直接求解了次临界流动状态下导电流体的控制方程，精确预测了Hopf分叉失稳的临界参数。本文预测三维Hopf分叉失稳的方法，避免了求解系统矩阵特征方程，克服了三维系统线性分析方法特征根求解困难的问题，相关方法和结果能够应用于超声速飞行器、风机、电磁冶金等领域的工程设计和设备运行控制。通过分析次临界流动状态下的流动特性，以及磁场对振荡速度、振幅衰减、频谱分布和Recr的影响规律，获得如下结论：

1） 速度振荡幅度的衰减速率对较小范围内的Ha变化响应异常迅速，磁场对速度振荡具有显著的抑制作用。随着Ha在一定范围（Ha=0～5）内的增加，速度振幅的衰减速率呈抛物线形式增加，振荡流动趋于更加稳定。

2） 磁场变化对次临界流动状态下速度振荡的无量纲角频率无影响。不同Ha条件下，速度振荡具有唯一主导的无量纲角频率，且均为无磁场作用下的无量纲角频率0.5752，反映磁场作用下流动状态由稳态流动转变为周期性振荡流动也同样是由Hopf分叉所引起。

3） 随着Ha的增加，发生第1次Hopf分叉的Recr显著增加，且呈抛物线增加趋势。