基于CST-GAN的翼型参数化方法
田洁华,孙迪,屈峰,白俊强
西北工业大学 航空学院,西安 710072
随着飞行器的经济性、安全性、环保性等各项性能指标要求的提高,气动优化设计在飞行器设计中占据越来越重要的地位[1-3]。其中,几何参数化方法的特性对优化设计的寻优区间和计算效率有着深刻的影响[4]。一个好的参数化方法,需保证最优解包含在设计空间中的同时,能够用尽量少的参数和足够高的精度来定义几何外形,以减少设计过程中的计算量。
传统的参数化方法,如Bezier曲线[5]、B样条方 法[6]、自 由 变形(FFD)法[7]、解 析 函数 叠 加法[8]、类别形状函数变换(Class and Shape Transformation, CST)法[9]等,往往需要较多的设计参数才能对翼型进行准确描述,这对依赖高精度CFD仿真的气动优化技术提出了巨大挑战。在气动外形优化中,越高的设计维度和越大的设计变量范围,会覆盖更广的设计探索空间,由此也会产生大量CFD计算问题,加剧“维数灾难”现象[10]。
为克服“维数灾难”现象,许多学者开展了对设计空间降维方法[11-15]的研究。张威等[16]使用主成分分析(PCA)方法,提取了翼型的主要几何变形模态,并以此作为设计变量,对RAE2822翼型进行了优化。Wu等[17]采用本征正交分解(POD)方法对CST基函数的系数进行降维处理,结果表明POD参数化方法可以用更少的参数个数,达到与高阶CST方法相近的翼型表示效果。此外,非线性降维方法也被应用于缓解“维数灾难”,吴则良等[18]提出了一种基于深度自动编码器(DAE)的神经网络模型,将该模型用于翼型参数的非线性降维,并与POD和CST方法进行对比,实现了更高的优化效率。
在大尺度设计空间中,可能包含较多奇异外形,使得优化过程对无效设计的探索次数增加,优化效率仍有较大提升空间。针对此问题,部分学者采用深度生成对抗网络对有效外形设计的分布进行学习,以进一步改善设计空间。Chen等[19]在Info-GAN中 融 入Bezier层 构 造 了Bezier-GAN,研究结果表明该模型能够减少设计空间中的奇异外形,提升优化效率。Du等[20]利用外形控制能力更好的B样条曲线,构造了BSpline-GAN,进一步提升了翼型表示能力。尽管如此,这些模型的性能依然受限于Bezier和Bspline参数化方法,需要较多控制点才能对翼型外形进行准确描述。
与Bezier和B-spline参数化方法相比,CST方法对翼型曲线有更加灵活的控制能力,能够用更少的设计变量较为精确的描述几何外形[21],其设计参数还具有明确的物理意义,可以方便地对前缘曲率半径、后缘角及后缘厚度进行控制[22]。为此,本文充分利用CST方法的优点,在Info-GAN中融入CST层,构造新的翼型表示方法:CST-GAN,以进一步提升翼型表示能力,减少设计空间中的奇异外形,从而提高优化效率,节约计算成本。
1 CST-GAN参数化方法
1.1 CST参数化方法
CST参数化方法最初由Kulfan等[23]提出,通过一个类别函数和一个形状函数来描述几何外形,用公式表示为
式中:ζ=y/c;ψ=x/c;c为翼型弦长;x为翼型x轴坐标;y为翼型y轴坐标;ζTE为翼型后缘相对y轴坐标。
类别函数可以表示为
N1和N2定义了所表示的几何外形的类别。美国国家航空咨询委员会(NACA)系列圆头尖尾翼型类别函数取N1=0.5,N2=1.0;对于双圆弧翼型,取N1=1.0,N2=1.0;Sear-Haack旋成体的类别函数则取N1=0.75,N2=0.75,如图1所示。
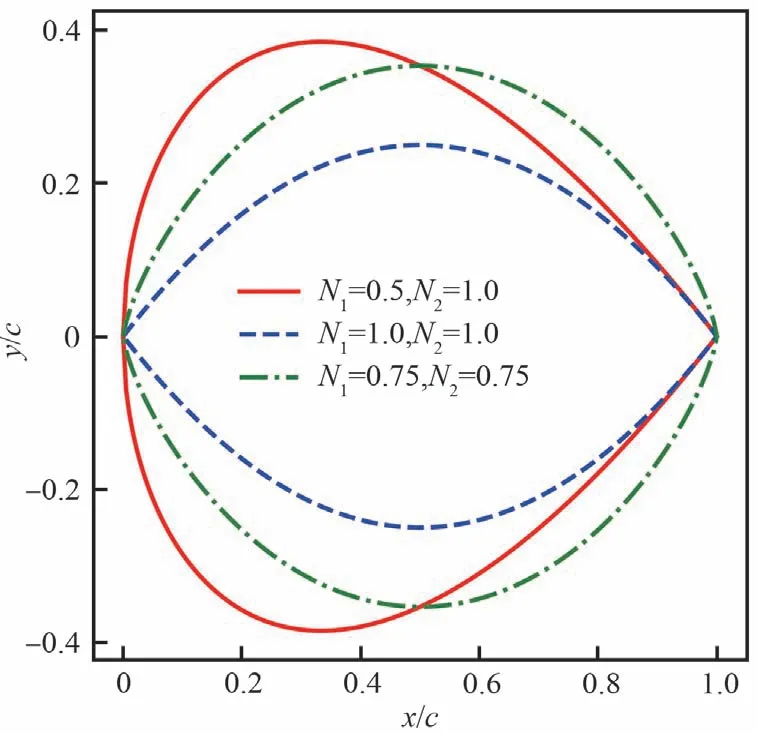
图1 类别函数定义的外形Fig.1 Geometric shape described by class function
CST方法的形状函数S(ψ)通常用n阶Bernstein多项式的加权和表示:
式中:Bin为Bernstein多项式,i为多项式中的指数,n为多项式的阶数;Kin为组合数;wi(i=0,1, … ,n)为权重因子,组成几何外形的n+1阶参数向量w。图2为形状函数不同基函数对应的曲线形状。
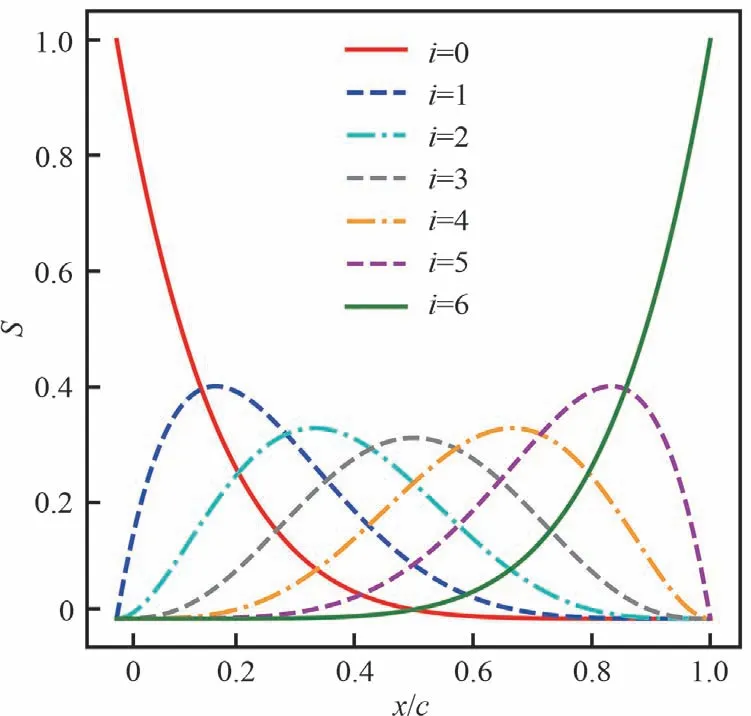
图2 形状函数的基函数曲线Fig.2 Basis function curves of shape function
在文献[23]中,Kulfan等提出并证明了形状函数在前后缘的取值分别与前缘曲率半径RLE、后缘角β和后缘厚度yTE有关,表示形式为
通过对CST函数进行推导,可得翼型前缘点曲率的精确计算公式为
忽略小量,可得近似公式为
式中:κx=0表示前缘点曲率;w0表示第1个CST参数;w1表示第2个CST参数。
1.2 生成对抗网络
生成对抗网络(Generative Adversarial Network, GAN)是GoodFellow等[24]于2020年提出的一种深度生成模型,如图3所示。生成器G以服从某种先验分布(如正态分布、均匀分布)的噪声z作为输入,生成与真实数据分布相近的样本G(z),判别器D则接收生成数据x~=G(z)和真实样本数据x,并辨别真假,其损失可以表示为
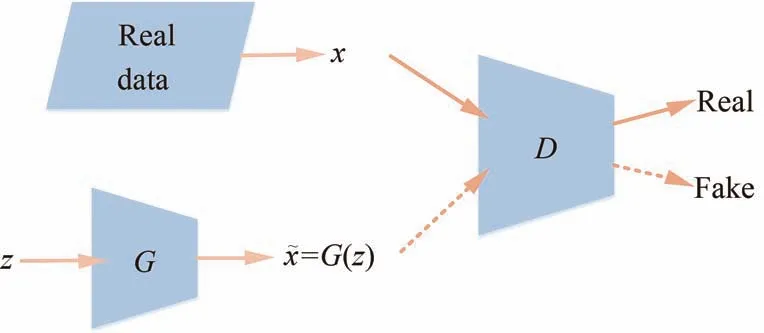
图3 生成对抗网络Fig.3 Generative adversarial network
标准生成对抗网络旨在学习样本的潜在概率模型并且生成符合该分布的数据,能够实现高维数据的低维表示。其学到的特征在数据空间中以一种复杂无序的方式编码,高度耦合,不具备可解释性[25]。为弥补该缺陷,信息最大化生成对抗网络(Info-GAN)[26]被提出,如图4所示。
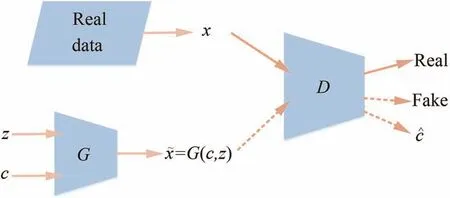
图4 信息最大化生成对抗网络Fig.4 Information maximizing generative adversarial network
Info-GAN的生成器以潜在变量c和不可压缩噪声z作为输入,在判别器末端不仅输出接收样本来自真实样本数据的概率,还输出对潜在变量的预测c^,通过最大化生成数据x~和潜在变量c之间的互信息I(c;G(c,z))来学习样本的可解释性特征,但由于互信息难以计算,故采用最大化其下界的方式来近似代替,互信息下界为
式中:H(c)表示潜在变量的熵值;Q是为了近似P(c|x)引入的辅助分布。对LI的详细推导可以参考文献[26]。Info-GAN的总损失函数表示为
这里的Pc是潜在变量的先验分布,λ是信息损失的权重参数。c的分布一般是固定的,所以H(c)可以作为一个常量处理。
1.3 CST-GAN参数化模型
GAN可以通过生成器G生成一系列离散点表示几何外形,然而,该离散表示无法保证翼型曲线是光滑的,此外,噪声变量所描述的几何特征高度耦合,不具有物理可解释性,很难为优化算法在设计空间中的探索提供有效反馈。针对这些问题,本文在Info-GAN的生成器中引入CST参数化层,构造了CST-GAN,以保证在学习可解释性特征的同时,能够生成光滑的翼型曲线。
通过对有效设计外形的分布进行学习,CST-GAN可以建立已知先验分布与有效设计外形分布的映射关系,进而对先验分布采样,通过生成器获得服从有效设计分布的翼型,以避免优化过程中出现奇异外形。
CST-GAN使用与Info-GAN相似的网络结构,并在生成器的末端添加了CST参数化层,如图5所示。在CST-GAN中,潜在变量c和噪声变量z作为生成器的输入,经过反卷积层产生控制翼型上下表面的参数wupper和wlower,最后通过CST层合成翼型外形。
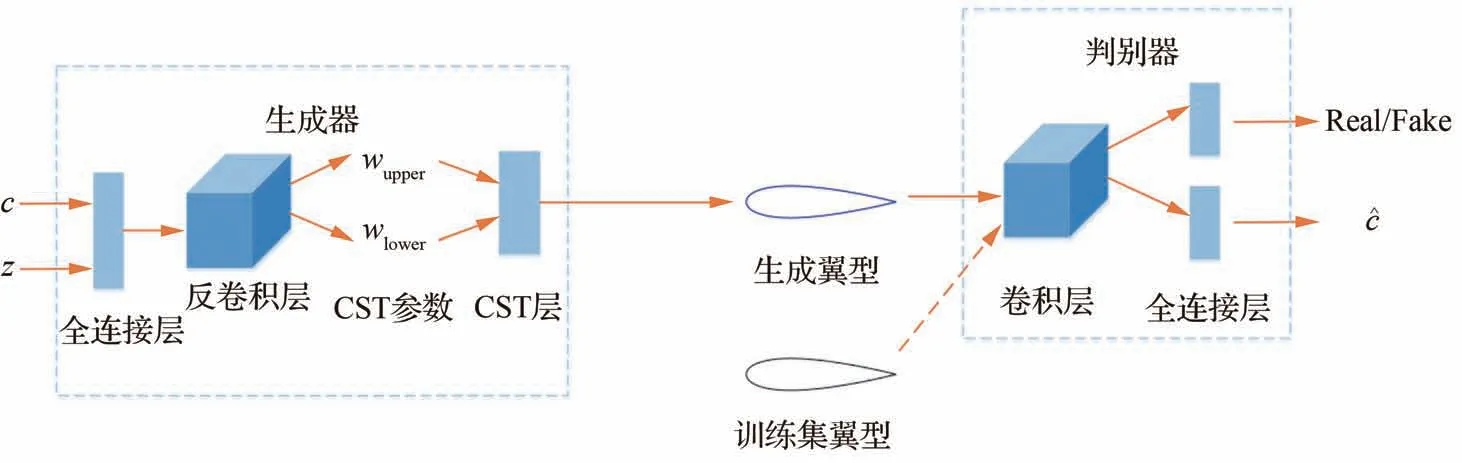
图5 CST-GAN模型结构Fig.5 Model architecture of CST-GAN
翼型x坐标为
式中:m表示CST曲线上的点数;x位于[0, 1]区间;y坐标按式(1)计算。
考虑到数值稳定性,CST方法中的Bernstein多项式为
式中:Γ表示数学中的gamma函数;exp为指数函数。
除了生成对抗损失和互信息损失,还添加正则项以进一步提高翼型生成效果。
1)翼型交叉损失
为防止生成翼型的上下表面出现交叉,在模型中添加如下正则项:
式中:N是批样本数量;m是CST曲线上点数;yki,l表示第k个样本下表面CST曲线上第i个点的y坐标;yki,u表示第k个样本上表面CST曲线上第i个点的y坐标。
2)前缘点曲率损失
为避免产生尖前缘翼型,添加如下正则项:
式中:w0,u和w0,l分别为控制翼型上下表面曲线的第1个CST参数。
综上,CST-GAN的总损失函数为
2 算例分析
2.1 模型训练
本文使用UIUC翼型数据库作为训练数据,该数据库约含有1 600个翼型。采用CST方法对翼型重新拟合,拟合后的翼型上下表面各有128个点,均为外形光滑的有效设计。
表1给出了CST-GAN的网络层设置。CST参数化层采用7阶Bernstein多项式,即生成器生成的翼型共由16个CST参数控制,类别函数取N1=0.5,N2=1.0。潜在变量服从均匀分布Pc=Unif(-1, 1),噪声变量服从标准正态分布Pz=N(0, 1)。对 于 式(15)中 的 参 数,取λ=1,λ1=10,λ2=10。采用Adam优化器[27]进行反向传播以更新梯度,batch size设置为32,训练步数设置为10 000,初始学习率为0.000 1。

表1 CST-GAN的网络层设置Table 1 Network layers setup of CST-GAN
图6为CST-GAN在潜在维度dc=3、噪声维度dz=8时随机采样翼型的几何外形及曲率分布。其中,k表示曲率。可以看出,由CST-GAN生成的翼型,其外形光滑,曲率连续,具有良好的几何性能。
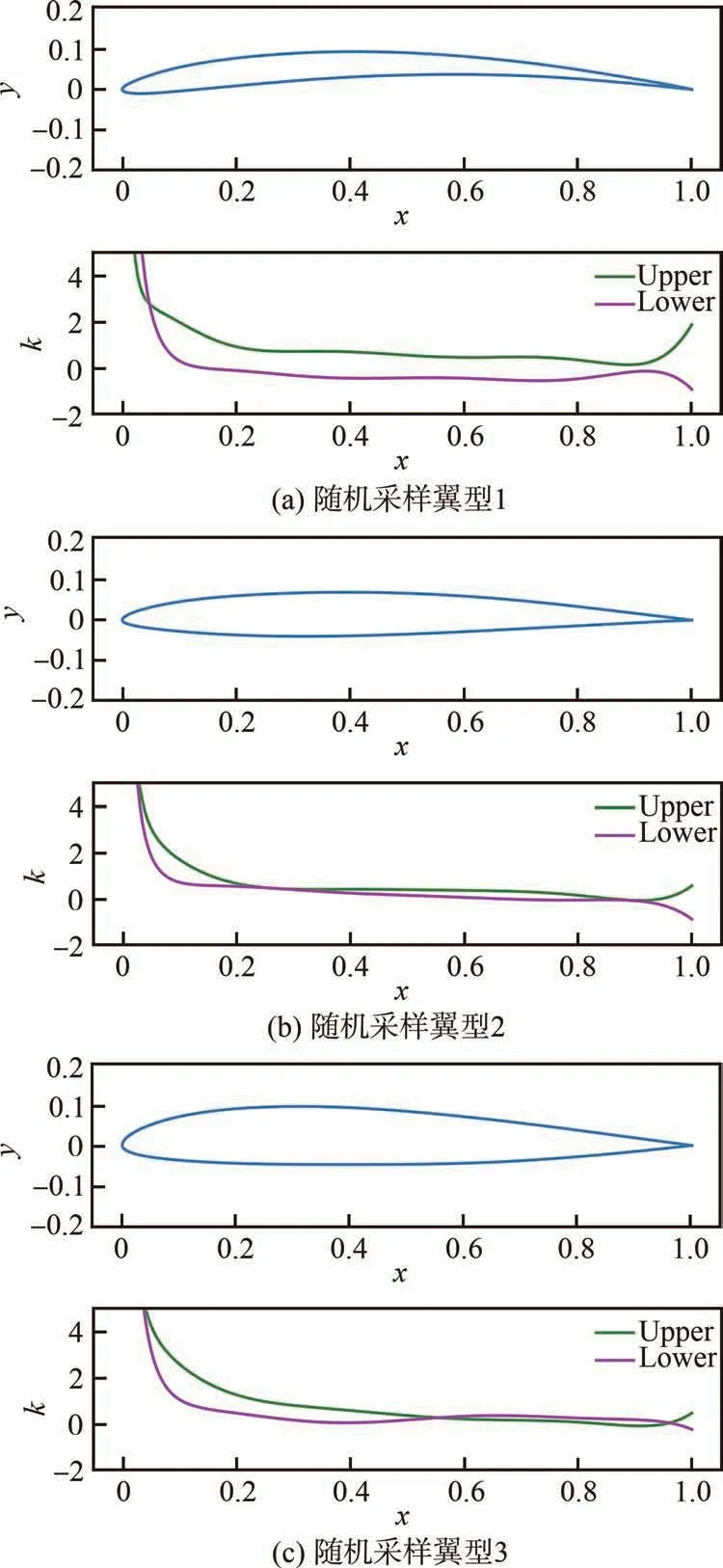
图6 CST-GAN生成翼型外形及曲率分布Fig.6 Geometric shape and curvature distribution ofairfoils synthesized by CST-GAN
图7给出了翼型外形随潜在变量c1、c2、c3和噪声变量z1、z2、z3的变化。当潜在变量均匀变化时,翼型的几何特征也呈规律性变化,比如在c2=0时,随着c3的增大,翼型厚度也逐渐增大,c1的改变则会引起翼型弯度的变化,而噪声变量只引起翼型外形的微小改变。这表明,CST-GAN方法的潜在变量可以描述翼型的主要几何特征,能够直观地反映翼型几何外形的变化,具有一定的物理可解释性,而噪声变量只能控制翼型外形的微小特征。
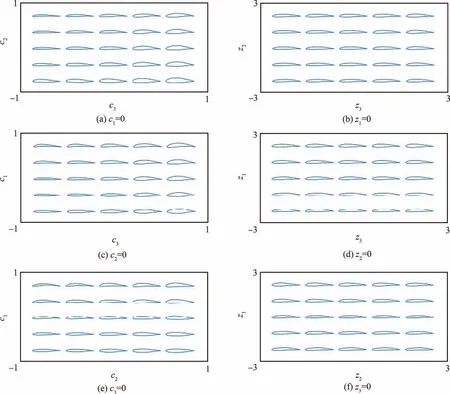
图7 翼型外形随潜在变量和噪声变量的变化Fig.7 Airfoil shape variation with latent code and noise variable
2.2 超参数影响
为了将CST-GAN应用于翼型优化设计中,进一步研究潜在维度和噪声维度对CST-GAN参数化的影响,以确定合理的设计变量数量,将主要从模型对数据的学习情况和翼型拟合精度2方面开展研究。
首先,本文采用最大平均差异(MMD)[28]评估生成设计的质量。MMD测量的是两个分布之间的相似程度,值越小,说明两个分布越接近,因而可以用来衡量生成数据与训练数据分布的相似性,评估模型对数据的学习程度。MMD的计算公式为
式 中:k(x,x′)=exp(-‖x-x′‖2/(2σ2))是 高 斯核函数;σ是核长度尺度,一般取为1。
图8为不同噪声维度下MMD随潜在维度的变化,可以看到,随着潜在维度增加,生成数据的质量也大幅提升,而在达到8个潜在维度后,提升的幅度减小。另一方面,当潜在维度较低时,噪声维度的增加会提高生成数据的质量;而当潜在维度较高时,噪声维度增加到一定程度反而会使生成质量下降,这是因为足够的潜在变量和噪声变量使得对翼型的表示能力趋于饱和,进一步增加设计维度反而会对模型的训练提出挑战,降低生成质量。此外,相比于噪声维度,潜在维度的增加引起生成质量提升幅度更大,这印证了图7得出的结论:潜在变量描述翼型的主要几何特征,而噪声变量只控制翼型外形的微小变化。
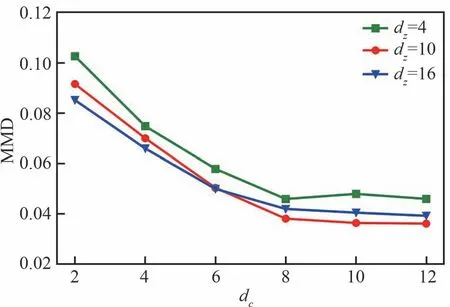
图8 MMD随潜在维度的变化Fig.8 MMD variation with latent dimension
根据以上分析,CST-GAN比较合理的潜在维度为8。进一步,在该潜在维度下,研究噪声维度对生成质量的影响,如图9所示。可以看到,MMD随噪声维度的变化较小,在噪声维度达到8之后生成数据的质量很难再有提升,因此,MMD评估结果表明,CST-GAN比较合理的潜在维度和噪声维度为8。
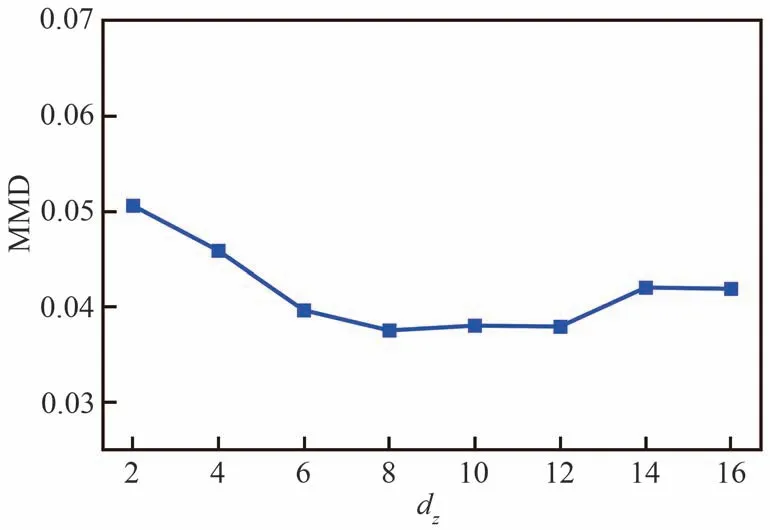
图9 MMD随噪声维度的变化Fig.9 MMD variation with noise dimension
其次,研究了潜在维度和噪声维度对CSTGAN翼型拟合精度的影响。由于CST-GAN对翼型的拟合无法解析求解,故而采用遗传算法[29](GA)通过迭代的方式获取使翼型坐标均方误差最小的设计变量。图10给出了在不同噪声维度下,潜在维度对翼型拟合精度的影响,这里用均方根误差(RMSE)衡量拟合精度。可以看到,随着潜在维度增加,翼型拟合精度逐渐提高,而在达到8个潜在维度后难以继续提升,这与图8的结果基本一致。在翼型拟合精度方面,CSTGAN比较合理的潜在维度为8。

图10 潜在维度对CST-GAN拟合精度的影响Fig.10 Influence of latent dimension on fitting accuracy of CST-GAN
图11给出了CST-GAN在潜在维度dc=8时翼型拟合精度随噪声维度的变化,以及与其他参数化方法的对比,这里采用均方差(MSE)作为拟合精度的衡量指标,注意横坐标为设计变量总个数。可以看到,CST-GAN的翼型拟合精度随噪声维度变化较小,当设计维度大于16时,拟合效果很难再提升。因此,CST-GAN比较合理的潜在维度和噪声维度都是8,与MMD评估结果一致,这也将在后文研究工作中采用。
此外,当设计变量数量小于18时,CSTGAN的翼型拟合精度明显高于Bezier和Bspline方法。PCA降阶参数化方法在10个维度以上对翼型的拟合误差最小,这是因为CSTGAN拟合翼型需要通过迭代来获取近似解,精度有所下降,而PCA方法通过求解最小二乘问题可以获得更高的拟合精度。然而,这并不妨碍CST-GAN具有更好的翼型表示能力和优化性能,本文后面的研究工作将对此进行证明。
2.3 几何空间与目标空间分析
通过几何空间与目标空间分析,进一步研究CST-GAN和其他参数化方法的翼型表示能力。
在本文中,PCA方法采用前10个主成分作为设计变量,取值范围对应UIUC翼型数据库的拟合边界。CST和FFD方法均以NACA0012翼型为基准翼型,采用16个设计变量对其扰动以获取新翼型。其中,FFD参数的扰动范围参考文献[19],取±0.2,CST参数的扰动范围取±0.5。CST-GAN则采用8个潜在变量和8个噪声变量作为设计参数,并按照对应的分布采样取值。
图12为不同参数化方法随机采样翼型的几何外形。可以看到,由CST-GAN采样生成的翼型都是外形光滑的有效设计,而PCA、CST、FFD方法依次出现了更多的奇异外形,表明CSTGAN具有较好的翼型表示能力。
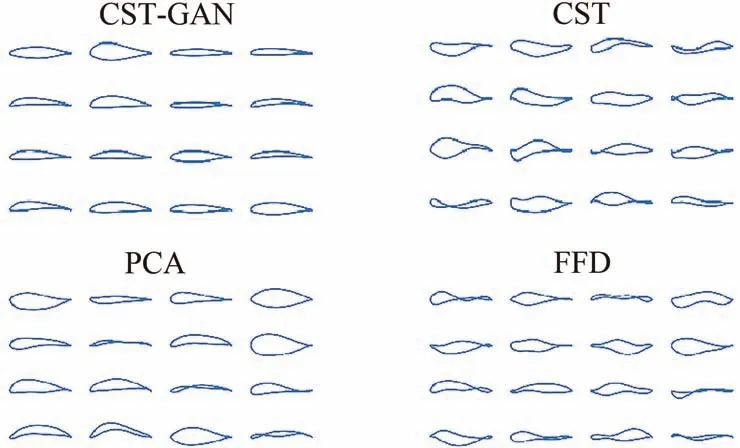
图12 随机采样翼型Fig.12 Airfoils by random sampling
图13为UIUC数据库和不同参数化方法随机采样1 500个翼型对应的目标空间。气动力均通过XFOIL[30]计算获得,图中(0,0)点表示交叉翼型或者XFOIL计算失败的翼型。可以看到,CST-GAN随机采样翼型的目标空间与UIUC数据库最接近,说明CST-GAN成功地学习到了样本数据的分布。CST和FFD方法的目标空间分布与UIUC数据库相差很大,出现了较多负升力和高阻力的翼型,这是因为它们的几何空间中含有较多的奇异外形,如图12所示。PCA方法在样本数据上对翼型进行了学习,使得其目标空间分布较CST和FFD方法有所改善,但由于PCA方法未能学到样本数据的真实分布,故与UIUC数据库仍有较大差别。
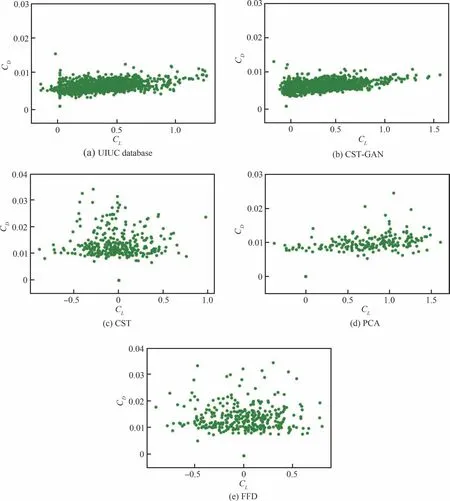
图13 随机采样翼型的目标空间Fig.13 Target space for randomly sampled airfoils
几何空间与目标空间的分析结果均表明,CST-GAN具有较好的翼型表示能力。
2.4 翼型外形优化
在表2描述的翼型优化算例上,对CSTGAN参数化方法进行测试。CST-GAN的设计参数包括8个潜在变量和8个噪声变量,其中,潜在变量c在[-1,1]内取值,噪声变量z在[-3,3]内取值。对于其他参数化方法,均沿用前文所述的配置。采用全局寻优性能良好的遗传算法(GA)作为优化框架,初代种群使用拉丁超立方采 样(LHS)[31]生 成,种 群 大 小 为36,共 优 化500代。翼型气动力通过XFOIL计算获得。

表2 优化算例Table 2 Optimization case description
对于每种参数化方法,各优化10次。图14为平均优化收敛曲线,表3列出了优化设计的性能参数,表4对比了不同方法的优化耗时,图15给出了不同方法的10次优化翼型和对应的升阻比。从优化收敛曲线可以看出,CST-GAN的初 代种群就含有较好的翼型设计,且在70代时基本收敛,具有最快的优化收敛速度,PCA次之,而CST和FFD直到300代才趋于平缓。这是因为CST-GAN采样生成的是外形光滑的有效设计,而PCA、CST和FFD方法依次出现了更多的奇异外形,如图12所示,使得在优化过程中对无效设计的探索次数增加,导致优化效率降低。同时,表4说明CST-GAN优化耗时最少,有效减少了计算成本。
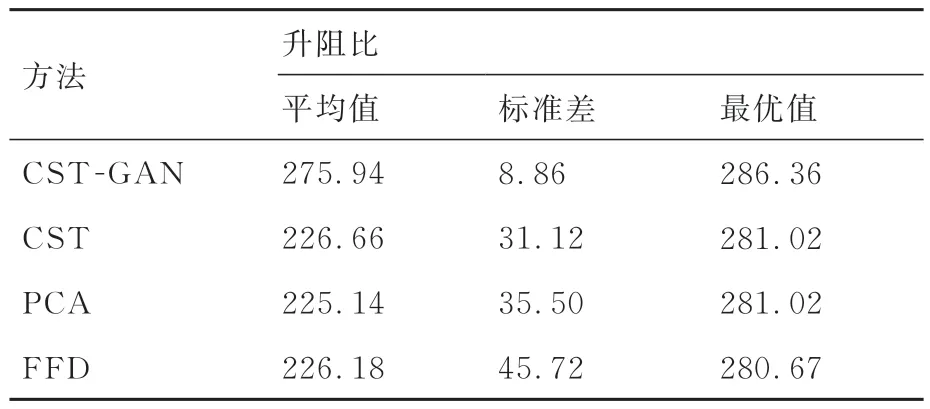
表3 优化设计的性能参数Table 3 Performance parameters of optimization design

表4 优化耗时Table 4 Time consumption after optimization
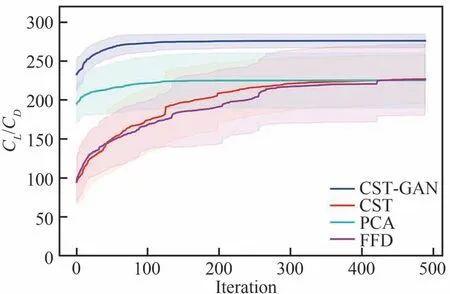
图14 平均优化收敛曲线Fig.14 Mean optimization convergence history
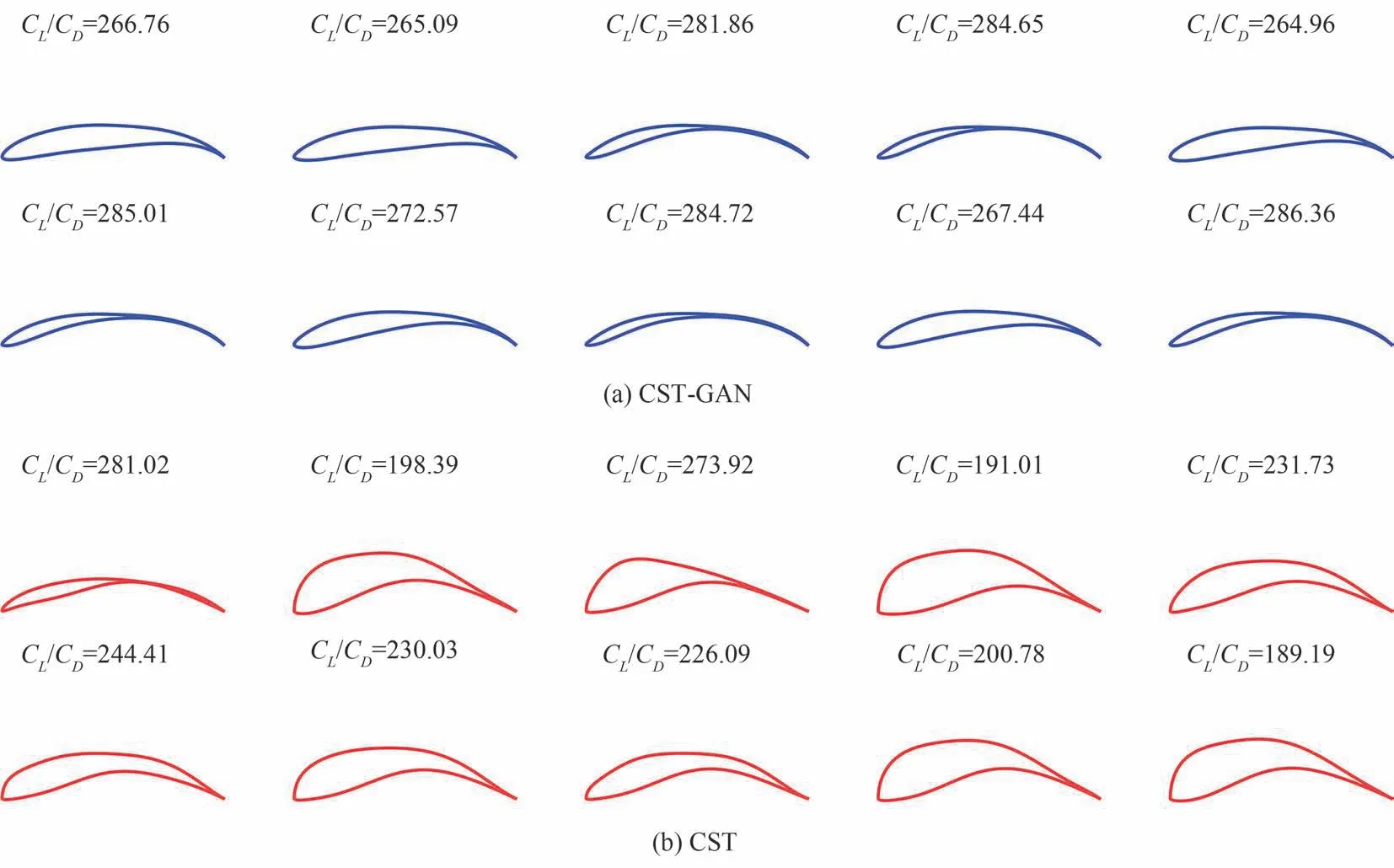
图15 优化翼型Fig.15 Optimized airfoils
图15表明CST-GAN优化的翼型外形更加光滑,表3则展示了CST-GAN较好的优化效果,对升阻比优化的平均值和最优值均领先其他方法,证明CST-GAN具有良好的翼型表示能力,可以提供有潜力的翼型设计。此外,CST-GAN多次优化的标准差为8.86,相对较小,说明CSTGAN的优化效果更加稳定。
这些结果充分表明,本文构造的CST-GAN具有良好的翼型表示能力,可以加快优化收敛速度,提高优化效率,节约计算成本。
3 结 论
基于UIUC翼型数据库,结合CST参数化方法和生成对抗网络,提出了一种更高效的翼型表示方法:CST-GAN方法。通过超参数影响研究、几何空间与目标空间分析发现,CST-GAN具有良好的翼型表示能力,最后基于该方法开展了翼型优化设计,得出如下结论:
1)CST-GAN可以生成外形光滑的有效设计,具有良好的几何性能。其潜在变量描述了翼型的主要几何特征,能够直观地反映出翼型外形的变化,具有一定的物理可解释性,而噪声变量只控制翼型外形的微小特征。
2)CST-GAN能够以较少的设计变量实现较高的翼型拟合精度,并能获得与样本集相似的目标空间分布,具有良好的翼型表示能力。
3)与其他几种参数化方法相比,CST-GAN可以实现更有潜力的翼型设计,获取更加稳定的优化结果,其良好的翼型表示能力,可以加快优化收敛速度,提升优化效率,节约计算成本。此外,该方法鲁棒性强,易于实现,有拓展至三维机翼及整机的参数化建模并进行气动优化设计的应用潜力。

