锻炼数学思维，掌握数学方法

汪静思

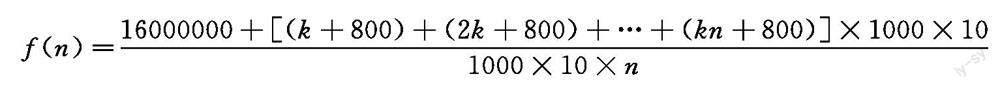
【摘  要】 数学思想方法是数学学科的精髓所在，所体现的是数学的本质，对于学生的数学学习有着重要的作用.正确地看待数学思想方法，并将数学思想方法渗透于数学课堂的教学中，有助于学生深度地理解数学知识，掌握数学知识的本质，促进学生深度学习的发生，促进学生数学核心素养的形成.本文以高中数学教学为例，就数学思想方法在高中数学教学中的渗透意义以及有效渗透方法进行分析，旨在强化高中生的数学思维能力，掌握有效的数学方法，提升数学学习的整体效果.

【关键词】高中数学；数学思想方法；课堂教学

在2022年版普通高中数学课程标准中明确地指出，数学课程教学要关注学生的数学思维能力培养，引领学生掌握有效的数学方法，促进学生在数学学习中的长远发展.数学思想方法是数学基本思想以及数学基本方法的统称，在数学领域中数学思想主要影响的是学习者的数学思维活动，而数学方法则是数学思想的具体化形式，在以数学思想方法培养为目标的背景下，要求学生对于数学的理解不只是停留在形式、层面上的浅层认识，更为强调的是学生对数学本质的掌握，提倡学生在数学学习中经历自主探索、逻辑推理、概念总结、结论总结等学习过程，在数学学习中积累并学会使用数学思想方法，能够轻松地解决数学问题^[1].

但是，我们发现在实际的课堂教学中，许多教师花费了较大的精力，但是收获到的教学效果并不明显，究其原因在于教师在教学中缺乏对学生数学思想方法思考的引导，学生无法在数学学习中建立完整的知识网络图，容易因为知识理解错误或者是没有掌握有效的数学方法造成做题失误.

对此，需要教师探索数学思想方法在高中数学教学中渗透的有效方法和途径，引领学生掌握高中阶段学生必须掌握的函数与方程思想、转化与化归思想、分数讨论思想、数学结合思想等，学会使用数学归纳法、待定系数法、类比法、辅助元法等解决问题，这不仅是众多教师关注的话题，也是本文研究的重点所在.

1  高中数学思想方法渗透的意义

1.1  促进数学教学改革

在对数学学科历史发展进程的研究中，发现数学史上的每一次突破性成就都与数学思想方法的提出与创新有关，可见数学发展的内在动力就是数学思想方法的不断衍生与开拓.但是，在近些年高中数學课堂教学中普遍存在重结果、重题型训练等问题，大部分教师照本宣科地讲述书本中的内容，学生招盘接受，此时学生只是掌握了数学基本事实，而忽视了书序的内容背后反映出的数学思想放方法，在这种情况下，需要教师创新教学方法.数学思想方法的渗透，要求一线教师更新教学思想，转变教学观念，主动地创新与优化教学方式，实现高中数学教学从重结果、重梯形训练转变为重过程、重思想方法培养，让高中数学课堂的变革紧跟教育新时代发展的潮流.

1.2  促进学生思维发展

数学常被誉为思维训练的体操，反映出的是数学思维训练对于学生数学学习过程中的各方面发展的重要影响，如对数学能力提升的影响，对数学思维品质形成的影响等.数学思想方法的渗透，可以诱发高中生在数学学习中实现思维的碰撞，形成创造性的想法，在数学思想方法的探索中领悟数学核心精神，并传承数学精神，塑造出优质的数学思维品质，优化高中生的数学思维结构^[2].

1.3  提升数学解题水平

解题是高中生数学学习中的主要内容，也是学生必须具备的数学技能，从数学解题的视角分析，学生解决一道数学题的过程是以一般性质问题为导向的寻求解决方法、得出结论的过程.数学知识的学习与积累是一个循序渐进的过程，需要学生不断地积累与完善，但是数学思想、数学方法是不变的，数学思想方法反映了数学的统一性，因此，需要教师在日常的教学中渗透数学思想方法，让学生掌握解题方法，无论题目的条件如何变化、题型如何转变，学生都可以轻松地解答问题，找出解决问题的关键点，灵活地运用数学方法解答问题.

2  高中数学思想方法渗透的有效方法

2.1  深入分析教材，掌握数学思想方法内容

章建跃在新教材培训会上表示，新教材能够助力学生的核心素养形成，在“明线”数学知识以及“暗线”数学思想方法上进行了有机地融合，能够引领学生在数学学习中获得螺旋上升的发展，树立理性精神，感受数学思想方法之美.在高中数学教材中主要包含了“观察”“思考”“探索”“归纳”等栏目，并在其中穿插了一些开放性的问题，引导学生使用归纳、类比、一般化、特殊化等方法，揭示出所学内容中反映出的数学思想与方法，因此，教师应深入地挖掘数学教材，找到数学思想方法的融合点，为数学思想方法的渗透奠定基础^[3].

例如 在“集合间的基本关系”这节课教学中，教材中首先提出了这样的问题：“我们知道，两个实数之间有相等关系、大小关系，如，，等等，两个集合之间是否也有类似的关系呢？”在“观察”栏目中出示了几个案例：（1）A= {1，2，3}，B= {1，2，3，4，5}；（2）C为立德中学高一（2）班全体学生组成的集合，D为这个班全体学生组成的集合；（3）E={x|x是两条边相等的三角形}，F={x|x是等腰三角形}，要求学生通过案例的观察，思考集合之间存在的相等或大小关系.通过对教材内容的分析，发现教材首先利用具体的问题启发学生，引领学生从两个实数之间的关系分析类比推理到两个集合之间的关系分析，有助于学生树立类比推理思想，在“观察”栏目中以三个例子为载体，让学生在经历观察、分析、抽象与概括的过程中，总结出集合之间存在的相等关系、包含关系，促使教师全面地掌握教材中蕴含的数学思想方法.

2.2  重视教学过程，加强数学思想的训练

在以往的数学课堂教学中，大部分教师只是将现有的数学知识讲解出来，并要求学生记住，却极少给学生提供自主探索的机会，导致学生无法从数学问题的探索中，感受到数学思想，这是影响学生数学学习质量提升的关键原因之一.为了解决这一问题，需要教师重视教学过程的优化，将教学的关注点放在学生的学习活动参与中，能够引领学生在数学问题的探索中，获得数学思想的训练，深化对数学思想的体验与感悟^[4].

例如 以“函数与方程思想的渗透”为例，为了帮助学生了解函数与方程思想，教师可以在课堂教学中给学生出示这样一道习题：“为稳定A市的房产价值，当地政府决定建造一批保障房供应社会.政府选择了一块土地作为建筑用地，需要花费1600万元购买，在此地可以完成10栋楼房的建筑，每栋楼的层数相同，且建筑面积均为1000米²/层，楼层数与建筑费用之间存在极大的关系，假设楼层数为x，那么建筑费用则为（）元，经过相关人员的测量，发现若将每栋楼建成层数为5层，那么这个小区的综合费用为1270元/米²，请学生计算：（1）求k的值是多少？（2）想要保障该小区每平米的平均综合费最低，应该将楼层盖到多少层最合适？最低的平均综合费用又是多少呢？”在这道题的解答中需要学生根据题意分析条件与结论，能够从题干中给出的众多条件中理顺各个数量之间的关系，并从中抽象出函数模型，可以帮助学生建立函数与方程思想，找到解题的关键.一名学生这样写道：

假设这个小区的每栋楼为n（n∈N*）层时，每平方米平均综合费用为f（n），由题意可以得到函数关系式：

.

列出函数关系式之后，学生开始解决第一个问题，结合题目条件中的数字关系“5”层、“1270”元之间的关系，抽象出函数表达式，即为=1270，那么：

.

计算得出：，在利用函数思想将优化问题转化为函数求最值问题，可以降低问题的难度，帮助学生进一步掌握函数与方程思想，提高学生的问题解答能力.

2.3  及时整理总结，概括与提炼数学方法

在高中数学思想方法的教学中，教师应注重引领学生在数学探索中提炼出数学方法，采取循序渐进的引导方式，立足于学生的认知规律，帮助在数学学习的过程中及时地概括数学方法，潜移默化地领悟数学方法的运用价值，并且能够在问题的解答中灵活地运用数学方法，发挥出数学方法的实用价值，提高学生的数学学习能力以及数学方法运用能力.因此，在每一课堂的结尾，教师都给学生预留几分钟的数学方法讨论与总结的时间，有意识地引领学生概括与总结数学方法，带领学生从“学会”走向“会学”，在数学学习中能够主动且创造性地探索新知，认识到数学的本质^[5].

例如 以数学归纳法为例，数学归纳法是一种用于判断命题对于某些自然数是否成立的演绎推理方法，详细的数学归纳法是：要验证命题P（n）成立的，要看命题是否满足以下两个条件：（1）当n取第一个数时，有成立，即为当时，P成立；（2）若自然数k大于等于时成立，即为成立；（3）证明也成立.为了帮助高中生在学习中掌握数学归纳法，教师可以借助“多米诺骨牌”游戏活动组织的方式，帮助学生理解数学归纳的证明过程，再通过问题分析的方式，让学生经历数学归纳法的分析、推理与验证过程，能够从问题推理与演算中进一步地总结与归纳出数学方法.如，教师出示例题“证明

等式对所有自然数n成立”，教师带领学生结合数学归纳法的证明条件，带领学生共同完成例题的证明过程：

（1）当时，；

（2）假设对任意自然数成立，即：；

（3）那么时，.

在经过三个条件的验证推理之后，学生们得出结论，即为当时，等式也成立，因此，对所有自然数都成立.通过这个典型例题的分析，引领学生在习题训练中及时地总结与提炼出数学归纳法，能够利用数学归纳法解答问题，证明等式是否成立，提升学生的数学学习效果.

3  结语

总之，数学思想方法在高中数学教学中的渗透，是新课改的重要内容，也是学生掌握数学关键能力的主要途径，需要教师积极地探索数学思想方法渗透的有效途径，引领学生在数学学习中掌握核心的数学思想，积累并掌握数学方法，能够在数学学习中对问题做出正确的判断，掌握问题解决的有效方法，帮助高中生攻克数学学习的难关.

参考文献：

[1]马艳波.新课程背景下高中数学变式题设计方法探析——以“数形结合思想在函数问题中的应用”一课教学为例[J].延边教育学院学报，2022，36（03）：143-145.

[2]王玉玲.高中数学常用数学方法及应用研究——评《高中数学思想方法的巧学活用术》[J].教育理论与实践，2022，42（27）：65.

[3]陈林.数学思想方法在高中数学解题中的应用[J].数学之友，2022，36（24）：61-63.

[4]萬飞.借助数学思想方法，解决几何问题[J].初中生世界，2023（Z1）：76-77.

[5]华锦梅.巧用数学思想方法 实现高效率数学课堂[J].试题与研究，2023（03）：22-24.