基于CUSUM 方法的集中供热管网泄漏故障诊断

周守军张国正刘臣林旭东曹长红

(1.山东建筑大学热能工程学院，山东 济南 250101；2.华能山东发电有限公司白杨河发电厂，山东 淄博 255200；3.淄博市博山区热力公司，山东 淄博 255200)

0 引言

城镇集中供热管道是城市地下管线的重要组成部分，相比于自来水管道，其应用时间短，但发展却较为迅速。 据统计，截至2019 年，我国运营的热水管网总长达48.8×104km，其中一次网长度为12.4×104km、庭院管网长为36.4×104km[1]。 由于管网的运行状况愈加复杂，保障这些管网的运行安全就显得尤为重要。 其中，泄漏是影响管网运行安全的主要问题，其主要原因包括腐蚀、设备老化、机械冲击等[2-3]，大量介质的泄漏会导致经济损失和环境破坏。 由于管道性能会随着时间的推移而降低，不可避免地产生局部泄漏，因此及时有效的泄漏故障诊断在实践中非常重要。

最初，我国大部分供热企业处于“先漏后检”的阶段，一般是由工作人员“听声判漏”，或结合管网压力变化试挖泄漏位置，这种方式的效率低、耗时长、成本高且定位不够精准[4]。 随着研究深入，管道泄漏诊断技术根据其作用的位置及实施手段主要可分为管道内和管道外诊断。 管道外诊断方法是将探测仪器置于在地表或管道外监测周围环境因素，获取数据并进行分析，从而及时地诊断泄漏的发生。杨汉瑞等[5]提出一种基于分布式光纤传感技术的膨胀节膨胀量的泄漏诊断方法，建立了有效反映膨胀量与温度变化关系的检测模型，从而诊断了泄漏位置，其诊断结果与膨胀量的测量误差相关。 吴晋湘等[6]利用红外热像仪和土壤湿度速测仪等记录异常管段沿线土壤的温度、湿度信息，分析管网泄漏和保温层破损时传热传质对管道上方土壤温湿度的影响规律，判定泄漏点位置。 PERPAR 等[7]利用土壤的温度梯度诊断供热管道的泄漏状况，其精度较高。 FRIMAN 等[8]通过无人机搭载遥感热相机，将检测到具有异常高温度的区域认定为泄漏区域，此方法可以自动分割影响检测结果的建筑物，从而减小误报率。 上述管道外诊断方法有一定的效果，但受外部环境因素影响较大，且大部分存在排查周期长、成本过高、实施过程复杂以及确定泄漏位置不够及时等缺点。

管道内诊断法发展源于20 世纪末，主要利用监测设备置于管内获取管网运行数据进行直接诊断，或结合其他学科开展数据分析及泄漏诊断。FILIPPINI 等[9]基于压力波和质量流量数据分析，直接诊断泄漏时间和泄漏位置，但其准确度较差。PÉREZ-PÉREZ 等[10]提出人工神经网络结合在线监测数据的管网泄漏诊断方法，利用模拟数据来训练人工神经网络，并结合数学模型估计管网阻力系数，得到较好的诊断结果，但所需数据量较多，对模型的精度要求也较高，且管网运行中的压力波动对泄漏定位的精度有较大影响。 石光辉等[11]利用高频压力传感器，通过捕捉管网泄漏瞬间形成的负压水击波，并根据小波分析方法得到负压波传播到传感器的时间，再以此定位泄漏位置，但供热管网距离长、分支多，负压水击波会产生较大的衰减，难以对其准确定位。

供热管网泄漏初期，补水流量及压力变化相对较小，泄漏情况难以确定。 累积和(Cumulative Sum，CUSUM)方法基于似然比推出，通过分段累积监测数据序列信息，将过程的较小偏移叠加，以达到“质变”的效果，从而实现对较小偏移的检测[12]。CUSUM 方法已成功应用于金融分析[13]、医学诊断[14]、地震探测[15]及给水管网爆管检测[16]等领域。文章提出利用CUSUM 方法和集中供热管网泄漏仿真模型，采用仿真模拟与实验研究相结合的方法，通过监测管网补水流量和压力开展泄漏故障诊断，旨在泄漏发生初期就能对供热管网进行泄漏故障报警和准确定位。

1 泄漏故障诊断方法及管网仿真

1.1 集中供热管网仿真模型

文章提出的泄漏故障诊断方法的基础是集中供热管网仿真模型[17-18]。 设任意一个供热管网，其支路数为m、节点数为n＋1，由网络图论理论、基尔霍夫定律、伯努利方程和管路特性方程，得到其水力工况仿真模型方程组，由式(1)表示为

式中A为管网关联矩阵(为n×m阶矩阵)；G为管段流量向量；B为管网的基本回路矩阵，为(m-n)×m阶矩阵；ΔH为管段阻力压降；S为管段阻力特性系数矩阵(m阶对角矩阵)；｜G｜为管段流量G的绝对值m阶对角矩阵；Z为管段支路中两节点的位能差向量；DH为管段的水泵向量，当管段不含水泵时，该管段DH＝0，当有水泵时，DH为水泵扬程；Q为管网各节点的净出流量向量，入流为正，出流为负。 当Q为零向量时，表示供热管网正常运行，管网各节点的出流量与入流量代数和为0，即管网为一个闭合环路；当Q中某元素为负值，表示该管网发生泄漏。

而S可由式(2)表示为

式中K为管壁的当量绝对粗糙度，对于供热管道，一般为0.000 5 m；d为管道内径，m；l、ld分别为管网计算管段的长度和局部阻力当量长度，m；ρ为管内流体介质的平均密度，kg/m3。

式(1) 对应的求解模型由式(3)表示为

式中M为马克斯威(Max Well)矩阵，是以B为基础的(m-n)×(m-n)阶的对称正定矩阵，M矩阵对应于一定的树，不同的树相对应的M矩阵也不同；ΔHk为基本回路管段压降代数和，当Gk为方程组的解时，其值为0。

上述管网仿真模型方程组包括正常工况模型、节点泄漏模型和管段泄漏模型。 其中节点泄漏是指泄漏位置在供回水干管到用户(换热站)的分支节点上，原管网的拓扑结构与正常工况一致，在节点泄漏仿真时，只需对该节点设定泄漏流量值即可。 管段泄漏是指泄漏位置在供回水干管管段上，在管段泄漏仿真时，泄漏位置处设置流量接近零的“虚拟用户”，将管段泄漏转化成“虚拟用户”的分支节点泄漏，管网拓扑结构发生改变，在其分支节点处给定泄漏流量值，建立虚拟节点泄漏仿真模型，即为管段泄漏模型。

1.2 基于CUSUM 方法的泄漏故障诊断方法

1.2.1 CUSUM 方法

假设x1，x2，…，xζ，…，xn为按顺序记录的一组过程监测样本数据，对这组数据做以下假设，由式(4)[12]表示为

式中H0为原假设，表示过程无变点；H1为备择假设，表示过程有变点；μ0、μ1分别为变点出现前后样本均值，变点即样本数据突变的点，对应供热管网中泄漏发生的点；σ为样本标准差，假设为定值；n为样本数据组别上限；ζ为变点发生处数据组别，ζ＜n。

H1对H0的似然比可由式(5)表示为

式中Ln，ζ为备择假设H1对原假设H0的似然比统计量；L(n，μ0)、L(n，μ1)分别为H0与H1的似然函数；f0(xi)、f1(xi)分别为H0与H1的密度函数。

上、下偏移累积和由式(6)表示为

1.2.2 泄漏故障诊断方法

文章提出的泄漏故障诊断方法是利用CUSUM方法监测管网补水流量变化，当管网补水流量累积和变化超过预定阈值时，即可发出报警信号，并确定泄漏发生时间及泄漏量，然后将泄漏流量带入管网泄漏仿真模型，对每个节点进行泄漏模拟计算，并根据给定的判定准则，比较分析采样压力表的实验运行值与仿真模拟值，确定泄漏位置。

(1) 诊断是否发生泄漏

①获取一定时间间隔(5 min)的管网补水流量监测数据序列qi，计算其均值μ0与方差σ0，并将数据序列标准化为yi，由式(7)～(9)表示为

②选取CUSUM 累积和报警阈值h和漂移参数k，计算上偏移累积和，由式(10)表示为

(2) 诊断何时发生泄漏以及泄漏程度

②根据泄漏开始时刻补水流量值q(is)和泄漏最大时刻补水流量值q(if)，计算最大泄漏流量Δqm＝q(if)-q(is)。

(3) 诊断泄漏发生的准确位置

①计算泄漏开始时刻is(正常工况)和泄漏最大时刻if(泄漏工况)各个采集点实际压力变化值ΔHMj和仿真压力变化值ΔHsimMj，由式(11)和(12)表示为

式中Mj为压力采集点序号，j＝1，2，…，r，其中r为压力采集点总个数；HMj(is)、HMj(if)分别为is、if时刻该采集点实际压力值，由实际数据得到；分别为is、if时刻该采集点仿真压力值，将最大泄漏流量代入泄漏仿真模型可以得到。

假设管网拓扑结构中所有分支节点都为泄漏点，则目标函数OFx由式(13)[19]表示为

式中x为节点编号；N为管网总节点数；OFx即为假设第x分支节点为泄漏点所得目标函数值；Mp(p＝j＋1，…，r)为序号大于Mj的采样压力表节点。

②比较所有的目标函数值OFx，找到其最小值OFmin，则对应节点为一级泄漏点

③利用二级管段泄漏模型，重复(3)中①和②，只计算一级泄漏点及其两侧的“虚拟节点”，找到最小目标函数值对应的节点，即为二级泄漏点，再根据与的具体距离L，准确定位泄漏位置。

具体泄漏故障诊断流程图如图1 所示。

图1 泄漏故障诊断流程图

2 管网泄漏实验与模型验证

2.1 实验系统

实验系统由集中供热实验管网和在线数据监测系统两部分组成(如图2 所示)。 实验管网包含18 个用户和3 个热源，热源由循环水泵和电加热水箱组成。 管道布置为上供下回，供回水管段对称布置，且二者管径相同。 定压方式为变频水泵补水定压，定压点为循环水泵入口处，在泄漏实验运行的过程中，可实现自动补水。

图2 集中供热实验管网示意图

实验管网各用户管段上依次安装有进口压力表、温度表、电磁流量计、调节阀、截止阀和出口压力表。 其中，截止阀用来模拟各用户阻力，调节阀用来进行实验管网初调节，使用户达到设计流量。 循环水泵的前后位置依次安装进口温度表、进口压力表、出口压力表、电磁流量计和出口温度表，补水泵处亦有进口压力表、电磁流量计和出口压力表。 在线数据监测系统即对上述各仪表进行实时监测并将实验数据采集、存储到MySQL 数据库中。

2.2 实验方案设计

文章进行单热源枝状供热管网泄漏工况模拟实验。 所用单热源枝状管网拓扑结构如图3 所示，其中n、s 分别表示节点和管段。 该管网包括1 号热源和18 个用户，共分为36 个管段、38 个节点。 实验管网设计总流量为18 m3/h，而每个用户设计流量为1 m3/h。

图3 单热源枝状实验管网拓扑结构图

实验管网共13 个泄漏点，根据距离热源由近到远、先节点后管段、先供水后回水的原则编号。 其中节点泄漏点为3 个，在用户的进口或出口节点，编号为1～3；管段泄漏点为10 个，在供、回水管路上各5 个，编号为4～13。 具体泄漏点位置及编号如图3所示(括号内编号表示泄漏点在回水管路)。

城市供热管网正常工况下补水流量不宜大于总循环水量的1%[20]，而补水流量＞5% 时，表明管网发生了严重泄漏，此时泄漏位置也相对容易被确定。为了验证文章泄漏诊断方法对不同泄漏工况的有效性，并使实验工况研究更丰富，此次实验根据不同泄漏率(泄漏流量占总流量的百分比)分为1.1%(工况1)、2.5%(工况2)、4.0%(工况3)和5.5%(工况4)4 种泄漏工况，13 个泄漏点共52 组实验。 每组实验分为正常工况和泄漏工况两部分，各运行1 870 s，数据采集频率为2.2 s/次。 采用自适应递推最小二乘滤波算法[21]对管网运行数据(主要包括压力、补水流量)进行预处理，消除噪声。

2.3 泄漏仿真模型实验验证

针对供热管网的正常工况，龚璞等[18]已经开展了模拟研究，而文章主要对一级节点泄漏模型和二级管段泄漏模型进行验证。

节点泄漏工况选择1 号泄漏点工况2，管段泄漏工况选择11 号泄漏点工况1。 将两组实验中泄漏工况数据各取300 组，计算其平均值，得到各节点泄漏工况下的运行压力以及循环水泵扬程、定压点压力、泄漏流量等数据；再将循环水泵扬程、定压点压力、泄漏流量分别代入已编译的节点和管段泄漏仿真模型MATLAB 程序中，得到管网各节点仿真与实验压力数据。 如图4(a)所示，节点泄漏工况下各节点压力实验值与仿真值的相对误差最大、最小值分别为4.71%和0.86%；如图4 (b)所示，管段泄漏工况下各节点压力实验值与仿真值的相对误差最大、最小值分别为4.64%、0.06%。 两级泄漏仿真模型最大相对误差均不超过5%，且从图4 中可以看出，仿真模型的供回水压力曲线与实验曲线的变化基本相符，说明仿真模型的准确性较高。

图4 不同泄漏工况实验与仿真数据对比

3 泄漏故障诊断方法实验研究

3.1 CUSUM 方法参数选取

在泄漏故障诊断方法中，阈值h和漂移参数k的选取至关重要。 如果参数选取过小，会使得泄漏报警灵敏度过高，可能会将管网正常状态显示为泄漏状态，增加误报率；而参数选取过大，又将降低灵敏性，可能会将管网泄漏状态误认为是正常状态，增加漏报率。 主要采用3 种方法选取h和k。

方法1 为基于公式的推导[22]，由式(14)表示为

式中α为误报率；β为漏报率；δ＝(μ1-μ0)/σ，为变点的标准化移位量。 此方法期望值为α≤10%、β≤5%。

方法2 为基于平均运行链长(Average Run Length， ARL)的选取[23]。 ARL 指从检测开始到检测出发生异常所需要的平均样本个数，取ARL 为150，得到h＝3.5、k＝0.5。

方法3 为基于经验值的选取[16]，h＝5σ，k＝1.015。

以3 号泄漏点的4 组工况为例，将上述3 组h、k参数值代入上述泄漏诊断方法，计算泄漏报警时间及最大泄漏流量。 泄漏报警时间结果见表1，最大泄漏流量如图5 所示。

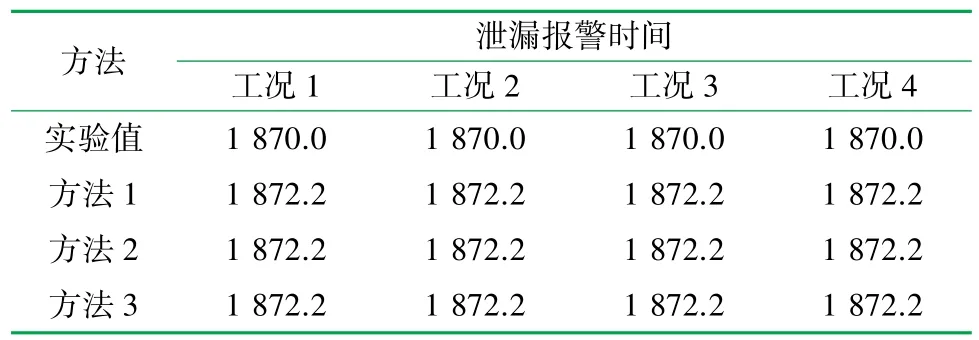
表1 不同方法所得泄漏报警时间单位:s

从表1 可以看出，3 组不同h、k值得到的泄漏报警时间一致，都是在泄漏发生2.2 s 后即发出报警信号，泄漏报警效果良好。 由图5 可以看出:工况1 和3中，方法3 得到的最大泄漏流量与实验值基本一致，另外两种方法计算值则比实验值要低；工况2 中，方法1 的计算值比实验值小，另外两种方法计算结果与实验值相等；工况4 中，方法3 计算值与实验值相等，另外两种方法计算值都比实验值稍低。 综上所述，方法3 的整体计算结果更接近实验值，故选择参数h＝5σ、k＝1.015 进行泄漏故障诊断方法的应用。

3.2 实验结果分析

3.2.1 泄漏报警计算

以3 号泄漏点4 组工况为例，按照上述方法对实验管网补水流量数据进行泄漏故障诊断，实验管网补水流量运行数据及CUSUM 累积和曲线如图6所示。 可以看出，当管网发生泄漏时，管网补水流量明显增大。 经过累积和计算，4 组工况在实验运行第1 872.2 s 时均有，并在此之后累积和不断增大，因此可以判定此时发生泄漏，与实际情况相符。

图6 补水流量运行监测数据及累积和曲线图

利用此泄漏诊断方法对13 个泄漏点共52 组泄漏实验计算了泄漏报警时间，发现所有工况实验均在实验运行第1 870.0 s 时发生泄漏，而计算结果显示泄漏报警信号发出的时间均为实验运行第1 872.2 s，没有误报、漏报或者延迟报警。 由于现有实验台的压力表采集频率最高只能达到2.2 s/次，若提高采集频率，报警时间还能缩短。

泄漏报警之后，计算管网泄漏流量。 从图6 可以看出，工况1 ～4，计算得到泄漏开始时刻is与实际时刻一致，泄漏最大时刻if也是泄漏工况运行稳定后的时间，所以两个时刻对应补水流量差值即为最大泄漏流量。

所有节点及工况最大泄漏流量诊断结果如图7所示，其中实验值是实验过程中管网最大泄漏流量值，计算值即为泄漏诊断得到的管网最大泄漏流量值。 4 种工况下计算值与实验值的误差均较小，其中相对误差最大值为1.6%，发生在2 号泄漏点工况1 和10 号泄漏点工况1，其余工况误差＜1.0% 。 泄漏流量计算值与实验值误差越小，说明最大泄漏时间if的计算也就越准确，这也为泄漏点位置准确诊断提供了良好的基础。

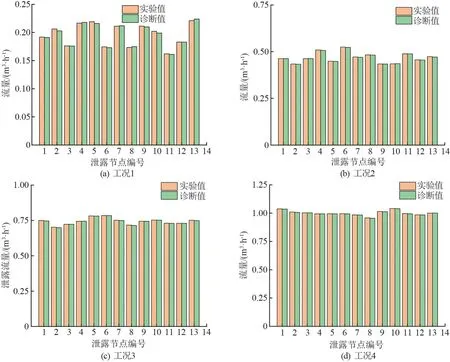
图7 管网最大泄漏流量诊断结果图

3.2.2 泄漏点位置诊断

根据泄漏位置诊断准则可以看出，选取合适的压力采集点，是准确定位的关键。 由于供热管网泄漏位置的出现没有规律可循，所以压力采集点的分布应当能反映泄漏发生后管网整体的压力变化，各个压力采集点距离过近或过远都有一定的局限性。 利用距管网热源近、中、远的采集点选取原则，详细对比分析不同的压力采集点分布方案，以期得到一个合理的分布。 具体分布方案见表2。

表2 不同压力采集点分布方案设计

将泄漏诊断所得位置与实际泄漏位置的误差距离分为l≤2 m、l≤4 m 以及l≤6 m，以方案1 为例，得到诊断结果见表3、4 及6(√表示诊断结果在误差范围内，×表示诊断结果在误差范围外)。

表3 方案1 泄漏位置诊断结果( l ≤2 m)

表4 方案1 泄漏位置诊断结果( l ≤4 m)

表5 方案1 泄漏位置诊断结果( l ≤6 m)

由上述泄漏工况实验条件可知，每组工况的泄漏位置诊断准确与否可视为随机事件，因此定义泄漏位置诊断准确率PA为诊断准确的工况数占总工况数的百分比[24]。 令PAi表示第i个方案的泄漏位置诊断准确率，各方案泄漏位置诊断准确率PA如图8 所示。 误差距离l≤2 m 时，PA1＝PA2＝PA5＞PA4＞PA3；误差距离l≤4 m 时，PA1＞PA2＞PA5＞PA4＞PA3；误差距离l≤6 m 时，PA1＞PA2＞PA3＝PA5＞PA4。

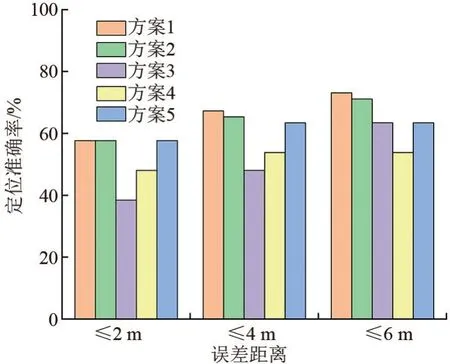
图8 各方案泄漏位置诊断准确率图

分析不同压力采集点方案诊断结果可以得到:

(1) 方案2 相比于方案1，减少了2 个压力采集点，但PA降低不多，而方案3 比方案1 增加了4 个压力采集点，反而PA降低较多，说明PA跟压力采集点个数有直接的关系，压力采集点个数过多或过少都会影响位置诊断效果；

(2) 方案4 与1 压力采集点个数相同，但位置分布不同，导致PA整体下降较多，说明当压力采集点个数固定时，分布位置太过靠近热源，也会使PA降低；

(3)方案5 与1 相比，只选取了供水管段上的3个压力采集点，采集点个数减少了3 个，但位置分布与方案1 一致，PA却发生下降，说明只在供水管段或回水管段设置压力采集点，都不能准确反映出泄漏工况发生时管网的整体变化，会影响泄漏位置诊断效果。

通过以上压力采集点分布方案的泄漏位置诊断准确率PA对比发现，压力采集点个数并不是越多越好，当管网规模较小，若压力采集点个数太多，则两点间距离近，因泄漏产生的压力变化并不明显，反而会对泄漏位置诊断结果产生较大影响，应该合理分布，使各压力采集点正确反映出管网泄漏时整体压力变化，这样才能使泄漏位置诊断结果更准确。

最终确定方案1 为最优方案，其误差距离l≤2 m时，PA＝57.7%；l≤4 m 时，PA＝67.3%；l≤6 m时，PA＝73.1%。 随着误差距离的增大，PA也增大，误差范围＞6 m 时，对诊断结果基本无影响。

泄漏位置判定的影响因素包括实验运行压力和仿真模拟压力。 其中，由于循环水泵工作点波动、仪表误差等，难以完全消除实验运行压力对泄漏位置诊断的影响；但仿真模型可以通过提高其精度、减小仿真模拟压力对泄漏位置诊断的影响，进而提高位置诊断准确度。

不论连续还是间断补水，只要能获取到补水流量监测数据序列，即可利用文章方法诊断泄漏故障。虽未验证环状供热管网，但环状管网与枝状管网在泄漏工况下的压力和补水流量变化规律一致，故文章方法对环状管网同样适用。

4 结论

基于变点理论中的CUSUM 方法，结合集中供热管网泄漏仿真模型，提出了一种包括泄漏报警、泄漏流量计算以及泄漏位置诊断的集中供热管网泄漏故障诊断方法，并利用MATLAB 软件进行了算法开发。 结合集中供热实验管网设计了实验方案，得到单热源枝状管网不同泄漏位置及不同泄漏流量下的压力与流量数据，并验证了该方法，得到结论如下:

(1) 在利用合适的CUSUM 参数值进行泄漏情况报警时，泄漏工况发生后2.2 s 即可报警，且没有误报和漏报，说明文章方法可以及时对管网泄露报警；

(2) 文章方法诊断所得泄漏开始时间准确，泄漏最大时间也是泄漏工况运行稳定的时间，对应计算得到最大泄漏流量与实验值相对误差最大仅为1.6%，说明方法对泄露时间和最大泄漏流量的诊断较为准确；

(3) 压力采集点的分布距离应该适中，采集点个数也并非越多越好，采用其中的最优方案诊断泄漏位置，其准确率可达73.1%，说明文章方法对泄漏位置的诊断准确率较高。