重心插值配点法求解BIOT 固结问题

赵晓伟王兆清李广惠商丽华

(1.山东建筑大学科研处，山东 济南 250101；2.山东建筑大学理学院，山东 济南 250101；3.商河县住房和城乡建设服务中心，山东 济南 251699)

0 引言

土体固结是一个相当复杂的过程，与土体类别、边界条件、排水条件和承载方式等有关。 BIOT[1]从弹性理论出发，研究了变形与孔隙压力的相互作用，确保土中应力和应变满足相容条件，给出描述比奥(BIOT)土体固结问题的偏微分方程组模型。 该模型已广泛应用于地质力学、水文地质学、石油工程[2-3]等领域。 但是使用解析法求解BIOT 固结微分方程组很困难，因此大多采用数值法求解。 目前，常用的数值方法有限差分法、有限元法和边界元法等。 赵维炳等[4]对BIOT 固结问题的研究采用的是中心差分格式。 但差分法对网格的规则性有要求，因此在固体力学领域受到了一定的限制。CHRISTIAN 等[5]结合有限元和有限差分法求解了BIOT 固结方程。 LEWIS 等[2]采用有限元方法研究了BIOT 理论模型，将其方程离散，再求解，并分析了地表沉降。 GASPAR 等[6-8]和BOOKER 等[9]利用有限差分方法离散了BIOT 的数学模型，并解决了多孔、分层以及二维准静态的固结问题。 WANG等[10-11]提出了一种基于Heaviside 阶梯函数的局部Petrov-Galerkin 方法以及径向基函数的无网格方法，求解BIOT 固结模型。 有限差分法和有限元法属于低阶的数值分析方法，想要计算出更高精度的结果，有限差分法差分步长要更小，而有限元法计算网格划分应更加稠密，这就降低了分析问题的效率。边界元方法虽可降低问题维数，简化问题分析，但其构造依赖于问题的基本解。 基于径向基函数的数值方法的原理是将径向基函数引入到未知函数的近似过程，这种方法虽然不用划分网格，但也有其局限性，计算精度过分依赖所选区的形状参数。

重心Lagrange 插值配点法是近年来兴起的一种无网格方法，是基于微分方程强形式的配点型方法。未知函数的近似函数采用离散节点上的重心型插值。 该方法已成功应用于求解不同类型的微分方程问题，其优点是数值计算稳定性好[12]、格式较为简单[13-14]、精度非常高[15-16]。 文章采用双变量重心Lagrange 插值公式近似未知函数，提出了求解BIOT固结问题的重心插值配点法。 对于与时间相关的初边值问题，传统配点型方法在空间域上用配点格式，在时间域上用差分格式，而文章在空间域和时间域上均采用重心Lagrange 插值配点计算，实现了微分方程初边值问题在时空域上的统一格式计算。

1 重心Lagrange 插值公式

u(x) 为定义在区间[a，b] 上的函数，其在节点a＝x1＜x2＜…＜xn＝b上的函数值为uj ＝u(xj)，j ＝1，2，…，n。u(x) 的重心Lagrange 插值由式(1)[17]表示为

重心Lagrange 插值基函数由式(2)表示为

则函数u(x) 的重心Lagrange 插值由式(3)表示为

由式(3)可知，函数u(x) 的m阶导数可由式(4)表示为

根据式(4)，u(m)(x) 在节点xi(i ＝1，2，…，n)处的m阶导数由式(5)表示为

将式(5)改写成矩阵形式，由式(6)表示为

一阶微分矩阵可以通过对式(2)求导直接得到，而高阶微分矩阵可以通过式(7)[18]的递推公式得到。

2 BIOT 固结问题的重心插值配点法

2.1 一维线性BIOT 固结方程

在一维固结情况下，经典BIOT 固结模型关于未知的流体压力p(x，t) 和土体骨架位移u(x，t) 的控制偏微分方程可由式(8)表示为

式中λ、μ为土体的Lame 系数；ne为孔隙率；β为流体的压缩系数；ke为土的渗透率；q(x，t) 为土体受力，N。

自由排水面边界条件由式(9)表示为

刚性的不可渗透面边界条件由式(10)表示为

初值条件由式(11)表示为

表示固结过程刚开始时水分变化为零。

将控制方程和边界条件无量纲化，由式(12)表示为

式中f(x，t)由q(x，t) 无量纲化得到。

边界条件由式(13)和(14)表示为

初始条件由式(15)表示为

2.2 BIOT 方程重心插值配点法计算公式

在空间域x方向和时间域t方向分别布置m和n个节点xi(i ＝1，2，…，m) 、tj(j ＝1，2，…，n) ，构成张量积型计算节点(xi，tj)(i ＝1，2，…，m，且j ＝1，2，…，n)，未知函数u(x，t) 和p(x，t) 在这些节点上的函数值为uij ＝u(xi，tj) 、pij ＝p(xi，tj) 。 其中，i ＝1，2，…，m；j ＝1，2，…，n。 利用重心Lagrange 插值公式，未知函数u(x，t) 和p(x，t) 近似由式(16)和(17)表示为

式中Li(x)、Mj(t) 分别为重心拉格朗日插值在节点xi(i ＝1，2，…，m)、tj(j ＝1，2，…，n) 上的插值基函数。

将式(16)和(17)的近似函数代入式(12)，可以得到

令式(18)在所有的计算节点(xi，tj) (i ＝1，2，…，m；j ＝1，2，…，n)上成立，得到式(19)为

注意到插值基函数性质Li(xr)＝δri、Mj(xl)＝δlj，并利用微分矩阵的记号，式(18)方程组的矩阵形式可由式(20)表示为

式中C′、D′分别为函数在节点xi(i ＝1，2，…，m) 、tj(j ＝1，2，…，n) 上重心拉格朗日插值的一阶微分矩阵；C″为函数在节点xi(i ＝1，2，…，m) 上的重心拉格朗日插值的二阶微分矩阵；Im、In分别为m、n阶单位矩阵；符号⊗表示矩阵的Kroneckor 积[19]；U、P为未知函数在计算节点处函数值构成的列向量，分别由式(21)和(22)表示为

裸模这个职业由来已久，陈小北倒没想到记者会问这个问题，他把目光投向叶晓晓，他以为她会简单地回答自己的身体漂亮之类的话。

令L1=-(C″⊗In)、L2=C′⊗In、L3=D′⊗C′、L4= -ke(C″⊗In)＋a(Im⊗D′)，则式(20)可以由式(23)表示为

可进一步由式(24)表示为

2.3 边界条件的离散和施加方法

求解式(24)的代数方程组，需要施加适当的边界条件。 考虑边界条件的离散问题＝-1、p＝0(x＝0，t∈(0，T))，其离散形式由式(25)表示为

式中C′1k为函数在节点xi(i ＝1，2，…，m) 上重心拉格朗日插值的一阶微分矩阵的元素。

式(14)的边界条件的离散形式由式(26)表示为

式(15)的初始条件的离散形式由式(27)表示为

式中D′1k为函数在节点tj(j ＝1，2，…，n) 上重心拉格朗日插值的一阶微分矩阵元素。

把式(25)～(27)的3 个方程附加到式(24)的方程组后，可以得到新的方程组，由式(28)表示为

3 数值算例

MATLAB 具有强大的矩阵计算优势，算例程序均用MATLAB 语言编写。 计算节点均采用区间[0，1] 上的Chebyshev 节点[20]，由式(29)表示为

通过坐标变换x＝(a＋b)/2 ＋t(b-a)/2 将式(29)的节点变换为任意区间[a，b] 上的计算节点。

一维固结问题示意图如图1 所示。 计算参数取值为渗透系数ke＝1、a＝neβ(λ＋2μ)＝0、f(x，t)＝0。该算例的解析解p(x，t)＝e-0.25tcos(10π/3)sin(0.5x)和u(x，t)＝-2e-0.25tcos(10π/3)cos(0.5x)。

图1 一维固结问题示意图

采用重心插值配点法求解该问题，在空间和时间区域采用相同数量节点计算。 不同数量计算节点的计算结果见表1，在厚度方向和时间轴上分别取10 个节点，计算得到的土体位移和孔隙水压力的数值解与解析解的最大相对误差的最小值分别为1.004 7×10-14和1.215 7×10-13，计算结果接近机器精度。

表1 不同节点数土体位移和孔隙水压力最大相对误差表

取13 个节点时，孔隙水压力p(x，t)数值解与精确解的相对误差pc，e如图2 所示；土体位移u(x，t)数值解与精确解相对误差uc，e如图3 所示。 在土体表面、中间和最底层处，时间从0 到1 的固结过程如图4所示。 在表面、中间和最底处，时间从0 到20 的固结过程如图5 所示。 由图5 可以看出，在t＝18 时，固结过程进入稳定状态。

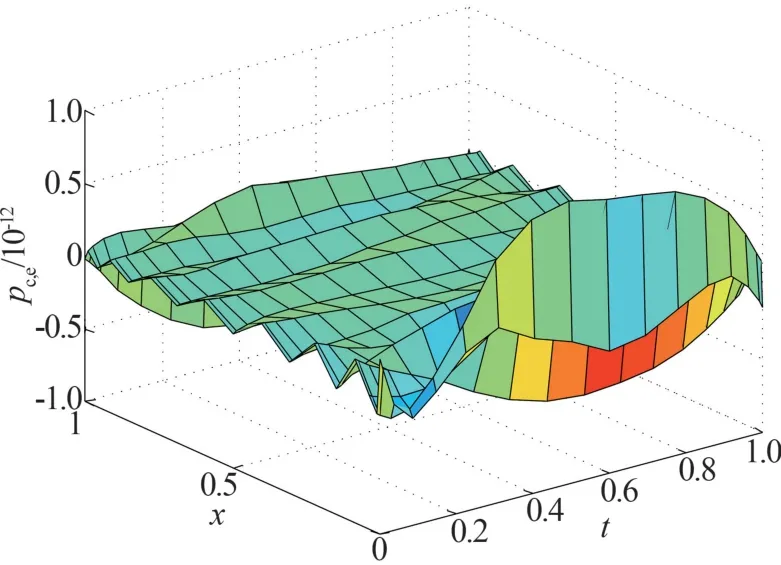
图2 重心插值配点法计算的孔隙水压力节点误差分布图

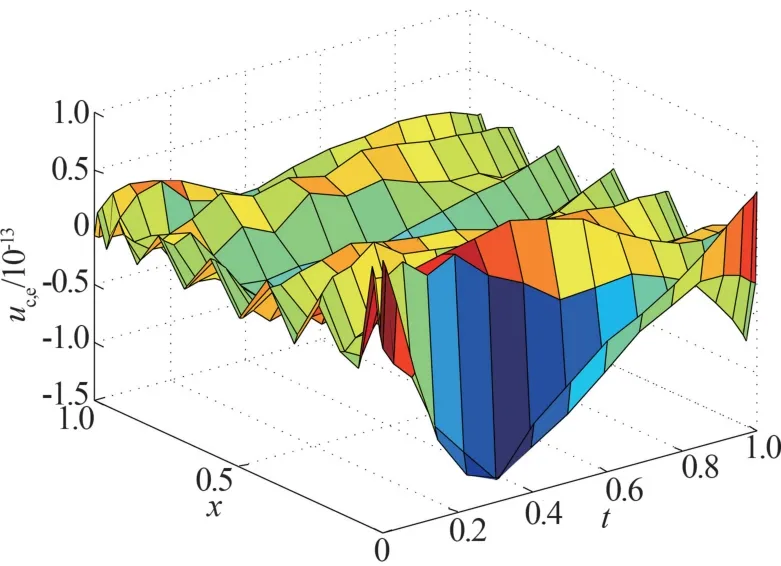
图3 重心插值配点法计算的土体位移节点误差分布图

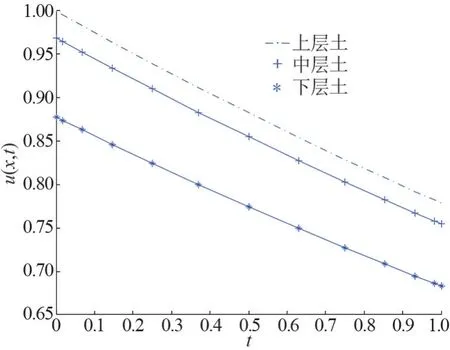
图4 土体固结过程图(t 从0 到1 )

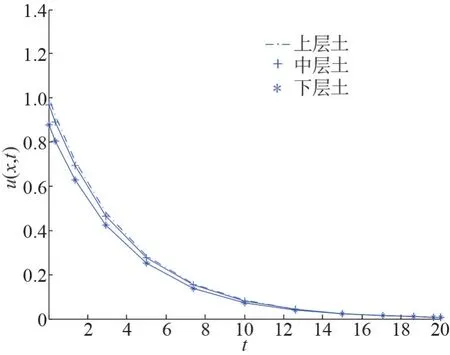
图5 土体固结过程图(t 从0 到20 )

该算例在选取节点数较少时，其位移和孔隙水压力的数值解与精确解的相对误差可达10-13～10-14，已经接近MATLAB 的机器精度，数值计算公式的正确性和计算方法的有效性由此可以得到验证，表明了该方法具有极高的计算效率。 当节点数量持续增加时，数值结果变化较小，表明该方法具有极好的数值稳定性。

4 结论

文章采用双变量重心Lagrange 插值公式近似未知函数，提出了求解BIOT 固结问题的重心插值配点法，并针对土体结构的BIOT 固结方程， 并通过算例验证，得到的主要结论如下:

(1) 采用重心插值配点法离散控制方程，不需积分计算，也不用划分网格，极大地提高了计算效率。 离散点的分布采用切比雪夫节点，可使计算结果具有良好的数值稳定性。 数值算例表明，所用重心插值配点法没有出现runge 现象，即使增加计算节点，计算结果依然具有稳定的、高精度的收敛特性，其计算误差非常接近机器精度。

(2) 所用重心插值配点法的计算公式用矩阵-向量形式表达，可使计算程序的编写过程变得简单，易于理解。 边界条件的施加采用附加法，将离散控制方程和边界条件约束的代数方程组合起来，任意的边界条件都可以用该方法实现。