城市公交网络级联失效分析

李树彬林兆丰孔祥科高佩佩陈孟飞

(1.山东建筑大学交通工程学院，山东 济南 250101；2.山东警察学院交通管理工程系，山东 济南 250014；3.山东轨道交通勘察设计院有限公司，山东 济南 250001)

0 引言

城市公交网络(Urban Public Transit Network，UPTN)作为城市交通系统的重要组织部分，是居民日常出行的重要交通载体，然而UPTN 时常受到自然灾害、交通事故等事件的影响，导致某些站点故障或线路停运，甚至网络大规模瘫痪，进而严重影响UPTN 的可达性和可靠性。 因此，如何提高UPTN的抗毁性受到人们的广泛关注。

ZOU 等[1]研究了佛山市UPTN 在静态与动态下的网络抗毁性，并提出基于最短路的负荷重分配方法。 HUANG 等[2]构建了基于耦合映像格子(Coupled Map Lattice，CML)的北京市UPTN 和公交-地铁复合网络级联失效模型，对比了2 种网络的抗毁性差异。 YANG 等[3]基于二值影响模型分析北京市公交-地铁复合网络的级联失效行为，研究发现级联失效规模随耦合参数和影响参数的增大而增大，并随着站点容差参数的减小而减小。 SU 等[4]以介数作为站点负荷分析了北京市公交-地铁复合网络抗毁性，研究发现当站点容量较低时，城市交通系统的效率存在非均衡相变。 ZHANG 等[5]提出了基于拥堵效应和用户均衡疏散的UPTN 级联失效模型。 DONG 等[6]提出了以Space-P 为上层逻辑层，Space-L 为下层物理层的双层UPTN 模型，并对其进行级联失效仿真分析。 MA 等[7]基于CML 模型研究了暴雨天气对公交-地铁复合网络级联失效的影响。 ZHANG 等[8]提出了改进Space-L 方法(考虑线路密度与相对发车频率)构建济南市加权UPTN，分析了网络在单站点攻击模式下的级联失效行为。 谢怡燃等[9]分析了我国5 个城市的UPTN 在有、无级联失效下的网络抗毁性。 沈犁等[10]研究了成都市公交-地铁复合网络在有、无级联失效下单条地铁线路停运的拥堵失效现象。 刘朝阳等[11]构建了基于全局分配的轨道交通网络级联失效模型，采用改进的边权函数表示站点状态的改变。 熊志华等[12]基于改进的CML 模型界定了北京市轨道交通网络拥堵传播范围，分析了拥堵传播特点。 张琳[13]从中观视角系统性地研究多模式公交系统级联失效的可靠性。 赵善男[14]研究了北京市公交-地铁复合网络的级联失效行为，并提出基于优先恢复度、介数和最大连通子图3 种策略。

现有关于UPTN 级联失效的研究主要存在着3点不足:(1) 传统的抗毁性度量指标并不能反映出级联失效的动态过程，难以挖掘出控制或优化级联失效的关键时步；(2) 认为站点负荷与容量存在线性关系，未考虑网络中存在着负荷较小却具有较大额外容量的站点，如新建或者偏远的公交站点；(3)未对容量参数的最佳取值定量化分析，局限于定性分析容量参数对级联失效的影响。 基于此，文章以厦门市公交网络为例，提出了3 种动态性的时段指标，构建了基于非线性负荷-容量的UPTN 级联失效模型；利用该模型分析网络在级联失效下的网络抗毁性，并采用控制变量法定量分析容量参数的最佳取值；对比了有、无级联失效下的网络抗毁性。 研究旨在为建设具有低成本和高抗毁性的UPTN 提供一定参考依据。

1 级联失效模型

当UPTN 中某些站点受攻击而发生故障时，由于受攻击站点的负荷和未到达的负荷需转移到相邻站点上，而相邻站点的容量受物理空间、设施水平等因素的限制并不能无限制增大，可能导致相邻站点的负荷超过其承载能力而发生故障，进而引起新一轮的负荷重分配，由此反复，最终可能导致大规模的站点故障甚至网络的瘫痪，如图1 所示。

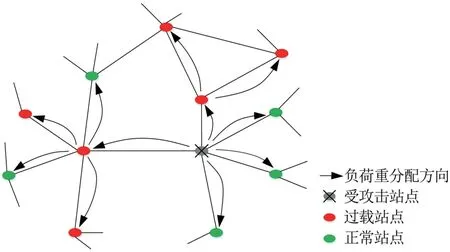
图1 级联失效示意图

1.1 UPTN 构建

文章采用改进的Space-L 方法[5，8，13，15]构建无向加权UPTN，构建说明如下:

(1) 将公交站点映射为UPTN 的节点，相邻站点间的线路映射为UPTN 的边[16]；

(2) 由于公交线路的上下行差异较小，统一将上行线路作为该线路的标准行驶线路，构建无向UPTN；

(3) 每条公交线路发车频率的设定都是公交运营公司根据乘客出行需求长期演化博弈的结果，因此发车频率可抽象地表示为特定时间段内客流的平均状态(非实际客流)[5，8，13，15]。 边权重为通过站点间各公交线路数相对发车频率之和，进而构建加权UPTN。 边权重由式(1)和(2)表示为

式中Rfi为线路i的相对发车频率；fi为线路i的实际发车频率，趟/h；p为UPTN 的总线路数量，个；Wi，j为边ei，j的权重；为线路n是否经过边ei，j，若线路n经过边ei，j，则＝1，若线路n未经过边ei，j，则＝0；Rfn为线路n的相对发车频率。

1.2 UPTN 站点初始负荷与容量

站点强度能更好地反映站点的负荷情况，因此文章将站点强度映射于区间(0，1)后的特殊归一化值作为站点的初始负荷[17-19]，由式(3)和(4)表示为

式中Si为站点i的强度；Γi为站点i的相邻站点集合；SLi(0) 为站点的初始负荷。

经典的负荷-容量模型(Motter-Lai，M-L)[20]认为节点容量与负荷呈正相关的线性关系，但在实际UPTN 中站点容量与负荷并非简单线性关系，存在着负荷较小的站点有着较大的未使用容量，如新建或偏远的公交站点。 因此，文章采用改进的M-L 模型[21]，通过容量参数α调节不同负荷站点的额外容量，使负荷较小的站点具有较大的额外容量，负荷较大的站点具有较小的额外容量，其负荷越接近于容量。 站点容量设置由式(5)表示为

式中SCi为站点i的容量；α、β为2 个容量参数，均位于区间(0，1]，当α＝1 时，该模型退化为线性负荷-容量模型。

1.3 UPTN 负荷重分配

文章定义UPTN 中的站点仅存在正常和故障2 种状态，将负荷小于容量的站点定义为正常站点，将受攻击站点、负荷大于容量的站点(过载站点)和孤立站点定义为故障站点，故障站点在级联失效期间不具恢复能力。

当UPTN 中某站点遭受攻击或其负荷超过其承载能力而转变为故障站点，丧失正常运转能力，所承担的负荷按相邻站点容量所占比例进行分配[13，17-19]，即相邻站点容量越大，所分配得的负荷量越大，负荷重分配公式由式(6)表示为

式中ΔSLi→j为站点i分配给站点j的负荷；SLi为站点i的负荷；SCj为站点j的容量；SCn为站点n的容量。

1.4 UPTN 级联失效传播

在T时刻，站点j接收站点i的部分负荷，在T ＋1时刻，站点j更新其承载的负荷，由式(7)表示为

式中SLj(T ＋1) 为站点j在T ＋1 时刻的实时负荷；SLj(T) 为站点j在T时刻的实时负荷。

若站点j更新后的SLj(T ＋1) ＞SCj，则级联失效继续；若SLj(T ＋1) ≤SCj，则级联失效终止。

1.5 UPTN 级联失效度量指标

为度量级联失效对UPTN 的破坏程度，文章以网络效率、网络最大连通率、故障站点比率和时段指标作为衡量级联失效规模的度量指标。

式中N为UPTN 的总站点数，个；di，j为站点i与站点j的最短路径长度。

(2) 网络最大连通率S网络最大连通率是衡量网络整体连通性的常用指标。 当网络遭受攻击或发生级联失效后，网络分离为多个子图或孤立站点，其中含有站点数量最多的子图为最大连通子图，其所含站点数量与初始网络总站点数量的比值称为网络最大连通率[22]，由式(9)表示为

式中N′为UPTN 最大连通子图所含站点总数，个。

(3) 故障站点比率R故障站点比率是衡量网络中站点损失程度的有效指标，定义为网络遭受攻击或发生级联失效后，当前网络故障站点总数与初始网络总站点数之比，由式(10)表示为

式中R′为UPTN 遭受攻击或发生级联失效后网络故障站点总数，个。

(4) 时段指标 上述3 种传统的度量指标均不能反映出级联失效的动态过程，难以挖掘出控制或优化级联失效的关键时段，因此文章提出时段指标，利用该指标可以全面地描述级联失效的动态演化过程，进而挖掘出控制或优化级联失效的关键时段。 时段指标是将每1 轮负荷重分配按时间先后划分为多个时段t，并记录每个时段内网络效率、网络最大连通率和故障站点比率的变化量。 时段指标分为时段网络效率ΔTE(t) 、时段网络最大连通率ΔTS(t) 和时段故障站点比率ΔTR(t) ，由式(11)～(13)表示为

式中TE(t) 为网络在时段t时的网络效率；TS(t)为网络在时段t时的网络最大连通率；TR(t) 为网络在时段t时的故障站点比率。

1.3 治疗方法 对照组入院后采用常规治疗，主要包括禁食、胃肠减压、解痉、止痛、降温、纠正水电解质紊乱、改善微循环以及预防性应用抗生素等。研究组则在常规治疗的基础上予以生长抑素（批准文号：H20020125，Laboratoires Serono S.A.）治疗，使用剂量3 mg/12 h，通过微量注射泵持续静脉给药，单位输液量0.25 mg/h，在患者临床症状缓解3 d后停药。

1.6 UPTN 级联失效模型仿真

文章级联失效仿真分为单站点攻击和循环攻击2 种模式，攻击策略采用蓄意和随机攻击策略(蓄意攻击为基于强度攻击)，结合上面的所述，级联失效仿真步骤流程如图2 所示。

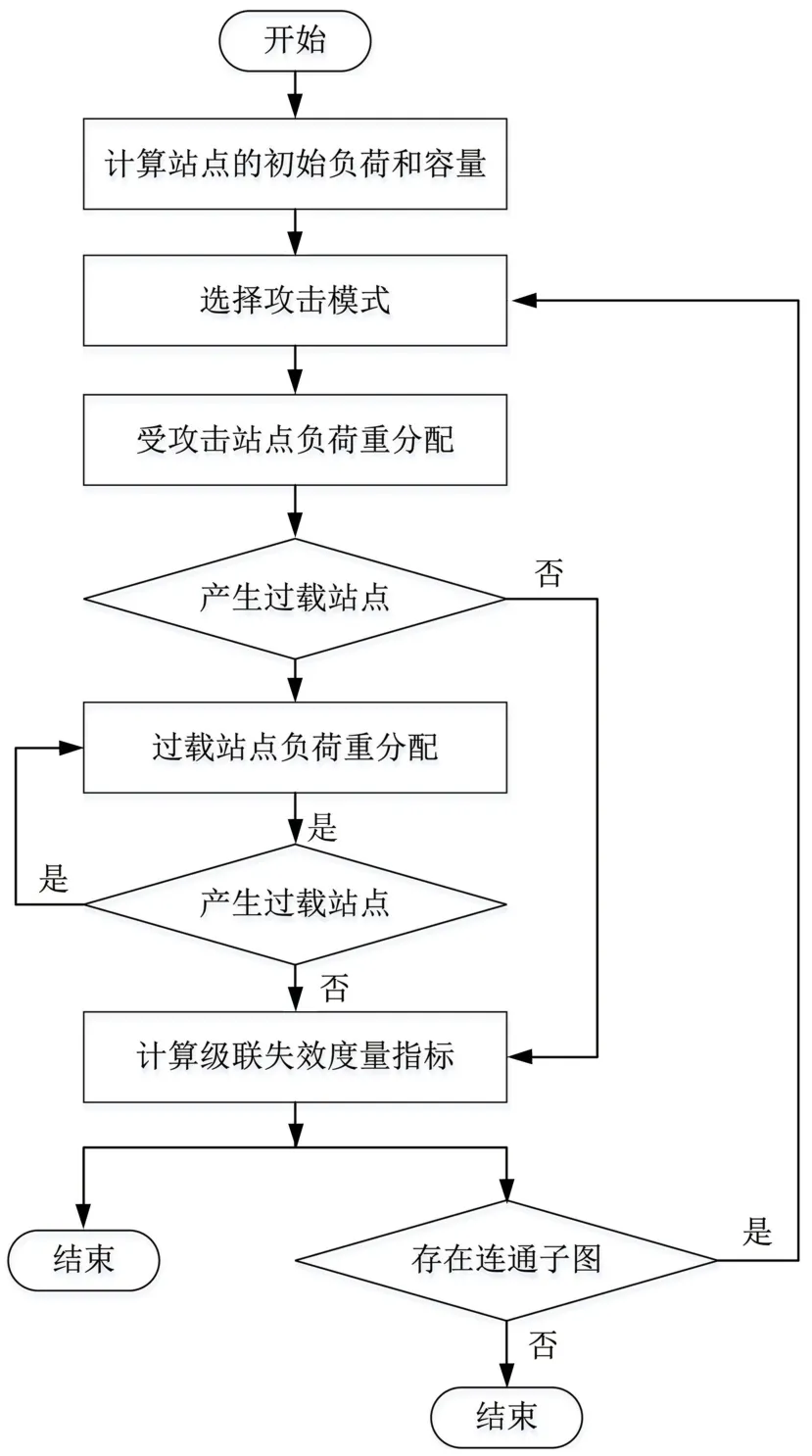
图2 级联失效仿真步骤流程图

(1) 单站点攻击模式为:①蓄意攻击 对强度进行降序排列，选取强度最高所在站点进行攻击。②随机攻击 通过Matlab 中Randi 函数生成随机序列，并选取随机序列首位所在站点进行攻击。

(2) 循环攻击模式为:①蓄意攻击 每次受攻击站点级联失效终止后，重新计算强度排名，选取当前强度最高的站点进行攻击，直至站点全为故障状态。 ②随机攻击 通过Matlab 中Randi 函数生成随机序列，依据随机序列依次选取站点攻击，若随机数选中的站点已为故障站点，则跳转到下1 个随机数，直至站点全为故障状态。

2 实例仿真分析

文章数据来源厦门市公交集团，选取2022 年7月厦门市(湖里区、思明区)183 条常规公交线路、659 个公交站点和早高峰(7:00—9:00)平均发车频率为样本数据，采用改进的Space-L 构建无向加权UPTN，UPTN 共计659 个网络节点，1 173 条网络边，借助Networkx 库可视化厦门市UPTN，如图3所示。

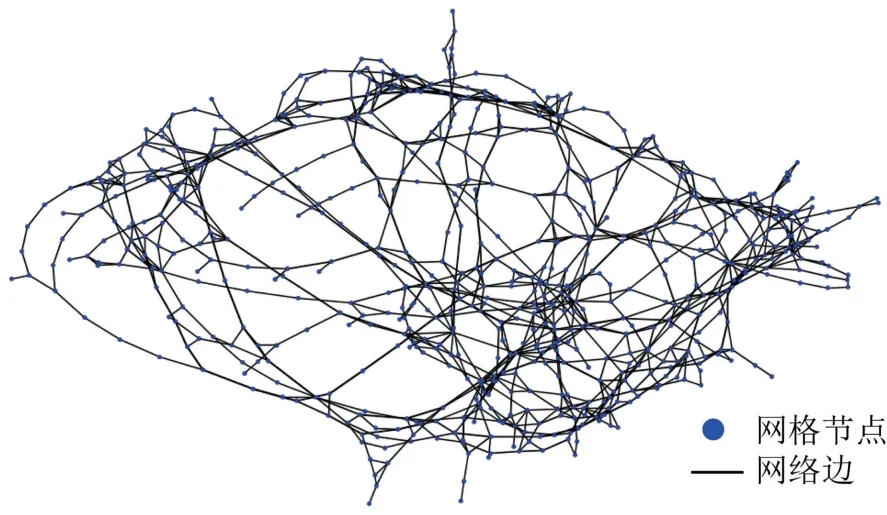
图3 厦门市UPTN 拓扑图

2.1 容量参数α、β 对级联失效的影响

负荷重分配公式(6)表明UPTN 中站点的容量与级联失效有着显著的关系，而站点容量受容量参数α、β的影响。 因此，容量参数α、β对级联失效规模大小有一定的影响。

采用基于强度的单站点攻击模式，以网络效率、网络最大连通率、故障站点比率和时段指标作为判断依据，采用控制变量法，探讨容量参数α、β对网络级联失效的影响。 容量参数α赋值范围为0.1～1，增量为0.1；容量参数β赋值范围为0.01 ～0.4，增量为0.01，每个容量参数α对应一组容量参数β，仿真结果如图4、5 所示。

图4 容量参数α 和β 对级联失效的影响图

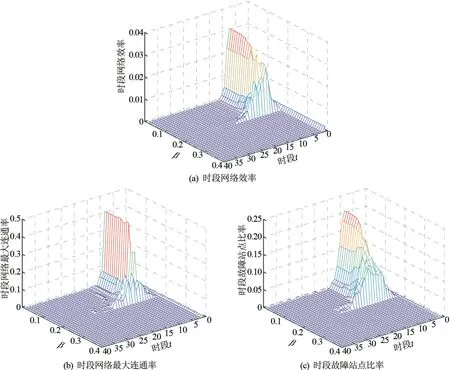
图5 时段指标随时段的动态演化过程图(以α ＝0.2 为例)

(1)β固定为0.18 时，由图4 可知:①当α＝0.1时，网络未发生级联失效，只有1 个站点(受攻击站点)故障，网络接近于初始状态(E＝0.131、S＝0.992、R＝0.002)；②当0.2≤α≤0.9 时，网络发生程度不一的大规模级联失效，网络基于处于完全瘫痪状态；③当α＝1 时，网络中所有站点均为故障站点，网络处于完全瘫痪状态(E＝0、S＝0.002、R＝1)。 这表明当β固定时，降低α可提高网络的抗毁性。

(2) 由图4(以α＝0.2 为例)可知:①当0.01≤β≤0.05 时，网络中所有站点均为故障站点，网络处于完全瘫痪状态(E＝0、S＝0.002、R＝1)；②当0.05＜β≤0.18 时，网络发生程度不一的大规模级联失效，网络基于处于完全瘫痪状态；③当0.18＜β≤0.19 时，网络抗毁性呈现出由大规模级联失效到未发生级联失效的突增现象(E:1.142×10-4➝0.131、S:0.008➝0.992、R:0.968➝0.002)，表明当处于β处于临界阈值(0.18)时，小幅增加β，网络抗毁性得到大幅度提升；④当0.19＜β≤0.4 时，3 项指标均未发生变化，网络中只有1 个站点(受攻击站点)故障，网络接近于初始状态(E＝0.131、S＝0.992、R ＝0.002) ，表明当β大于临界阈值后，即使β有较大的增加，网络抗毁性也不会有进一步的提升。

(3) 由图5(以α＝0.2 为例)可知:①当0.01≤β≤0.18 时，网络均出现级联失效现象，而当β＞0.18时，网络在时段1(经1 轮负荷重分配)后终止，网络未发生级联失效，这也进一步验证β的临界阈值为0.18；②3 种时段指标随时段的增加，大体呈现由缓慢上升到急剧上升的趋势，这说明初期时段未造成大规模站点故障，而随着时段的增加，多个站点的负荷逐步累积到超过其承载能力，进而出现突发性的大规模站点故障现象；③级联失效规模集中于时段域8 ～10( ΔTE＝0.031、 ΔTS＝0.42、 ΔTR＝0.209)，这说明时段域8 ～10 是控制和优化级联失效的最佳时段域。

由上述可知，在单站点攻击模式下，容量参数α的减少或β的增加，对网络抵抗级联失效能力有着显著的提升；特别地，当β处于临界阈值时，小幅增加β，网络抗毁性提升效果更为明显。 当容量参数设置不合理时，仅攻击强度最高的站点，就能引起网络几近瘫痪。 因此，合理的容量参数设置和关键站点的保护，对网络的正常运行尤为重要。

2.2 UPTN 抗毁性测度

UPTN 中站点的容量越大，抵抗突发事件的能力越强，然而站点容量的提升，必定带上成本的上升。 因此，如何较为合理地设置站点的容量，有效地提高网络的抗风险能力显得尤为重要。

网络抗毁性测度基于强度的循环攻击模式，以网络效率、网络最大连通率、故障站点比率作为判断依据，采用控制变量法，定量分析容量参数α、β的最佳取值。 容量参数α赋值为0.2，容量参数β赋值范围为0.3～0.8，其增量为0.1，探讨最佳容量参数β，仿真结果如图6 所示。

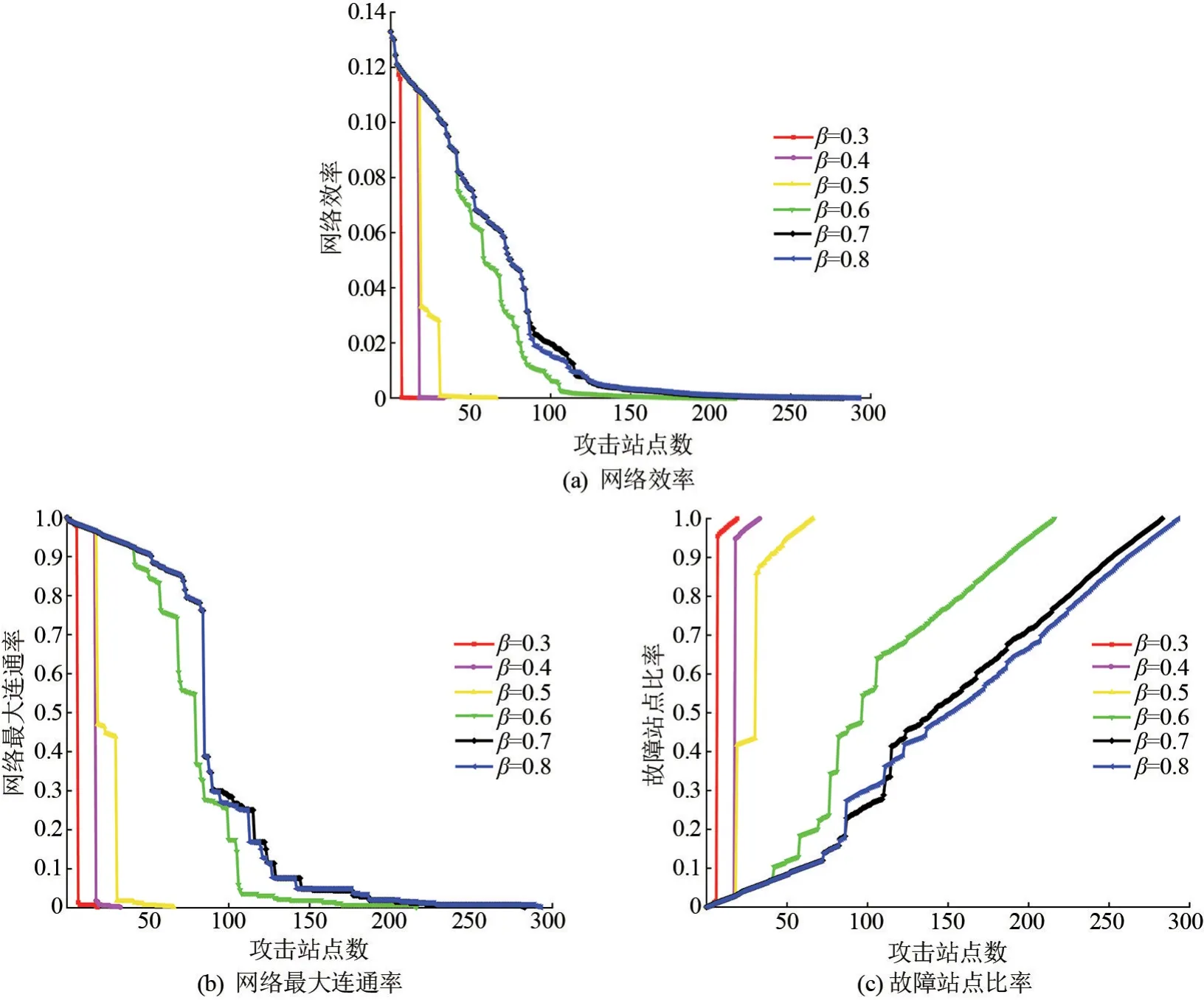
图6 容量参数β 对级联失效的影响图

(1)β固定为0.3，当攻击站点数为6 时，网络仍具有较高抗毁性(E＝0.116、S＝0.979、R＝0.015)，而当攻击站点数提升至7 时，网络抗毁性出现骤降现象(文章将这种明显的骤降现象称为网络结构突变)，此时网络接近完全瘫痪(E＝1.906×10-4、S＝0.014、R＝0.954)，这表明故障站点经一定数量的累计之后会出现突发性多站点失效。

(2) 对比β:①当β＝0.3 时，网络结构突变发生于攻击站点数6➝7，故障站点比率上升93.9%，网络最大承受攻击次数为19 次；②当β＝0.4 时，网络结构突变发生于攻击站点数17➝18，故障站点比上升92.1%，网络最大承受攻击次数为33 次；③当β＝0.5时，网络结构突变发生于攻击站点数18➝19、30➝31，故障站点比率分别上升38.9%、42.5%，网络最大承受攻击次数为66 次；④当β＝0.6 时，网络无明显的结构突变，网络最大承受攻击次数为216 次。 这表明随着β的增加，网络可以更好地抑制和延缓网络结构突变现象，从而提高网络抗毁性，特别地，当β＝0.5 时，小幅增加β，网络抗毁性有着显著的提升。

(3) 对比β＝0.7 和0.8，两者在各项指标下曲线近似重合，网络均未有明显的结构突变，网络最大承受攻击次数分别为283、293 次，仅相差10 次攻击。 这表明当β＝0.7 时，继续增加β，网络抵抗级联失效能力无法得到显著的提升。 综合考虑经济成本与网络抗毁性，最佳容量参数β取0.7。

同理，容量参数β赋值为0.7、容量参数α赋值范围为0.6 ～0.1，其减量为0.1，探讨最佳容量参数α，仿真结果如图7 所示。

图7 容量参数α 对级联失效的影响图

(1) 对比α:①当α＝0.6 时，网络结构突变发生于攻击站点数41→42，故障站点比率上升88.8%，网络最大承受攻击次数为55 次；②当α＝0.5 时，网络结构突变发生于攻击站点数41→42，故障站点比上升率87.4%，网络最大承受攻击次数为59 次；③当α＝0.4、0.3 时，网络均无明显的结构突变，网络最大承受攻击次数分别为179、239 次。 这表明随着α的减少，对级联失效的扩散有明显的遏制作用，特别地，当α＝0.5 时，小幅减小α，对网络抗毁性有着明显的提升。

(2) 对比α＝0.2 和0.1，两者在各指标下曲线变化类似，网络均无明显的结构突变，网络最大承受攻击次数分别为283、296 次，仅相差13 次攻击，这表明当α＝0.2 时，继续减小α，不能显著地提高网络抗毁性。 考虑到α处于站点容量设置公式(5)的指数部分，其扩容成本提升远大于β的扩容成本提升，因此最佳容量参数α为0.2。

由上述可知，在循环攻击模式下，容量参数α的减小或β的增加，可显著地提高网络抗毁性。 对比不同容量参数组合下级联失效度量指标的变化情况，当α＝0.2、β＝0.7 时，为最佳容量参数组合，网络在成本资源消耗较低的同时实现了较高抗毁性，可抵挡283 次蓄意攻击。

2.3 URTN 级联失效与非级联失效分析

非级联失效是指在不考虑站点间的相互影响下，当网络受到内外部干扰或突发事件等影响时，网络仍能保持正常运行的能力，也称为静态抗毁性，而级联失效与非级联失效的显著区别是其存在着站点间的传播动力学(负荷重分配)，级联失效模型的抽象描述也更接近于实际交通情况，也称为动态抗毁性。

基于级联失效与非级联失效2 种攻击模式，采用随机攻击和蓄意攻击作为两者的攻击策略(蓄意攻击为基于强度攻击)，以网络效率和网络最大连通率作为判断依据，研究对比网络在级联失效与非级联失效情况下抗毁性的差异。 选取最佳容量参数组合(α＝0.2、β＝0.7)进行级联失效仿真。 非级联失效下的蓄意攻击:每次攻击单个站点后(不考虑站点间的负荷重分配)，重新计算强度排名，选取当前强度最高的站点进行攻击，直至网络完全瘫痪。非级联失效下的随机攻击:依据Matlab 生成随机序列，依次选取单个站点攻击，直至网络完全瘫痪后终止。 仿真结果如图8 所示。

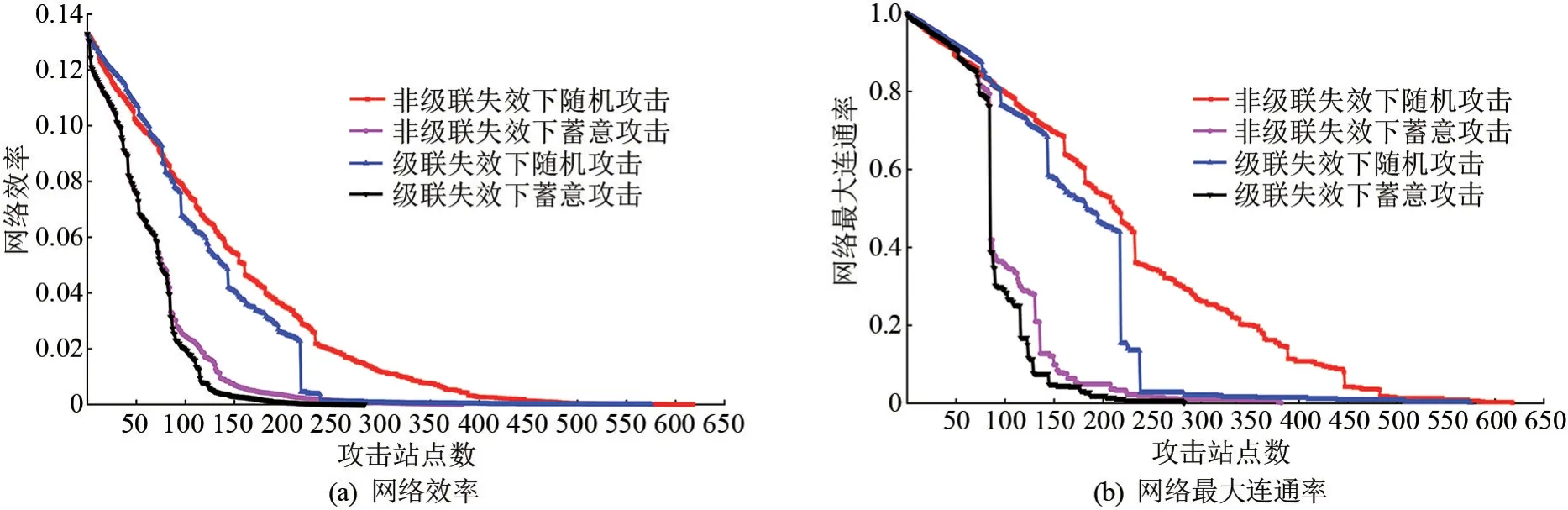
图8 网络在级联失效与非级联失效下度量指标变化图

(1) 在非级联失效下:①随机攻击E和S下降较为缓慢，当随机故障站点数目较少时，对网络整体的运行能力影响较小，但当随机故障站点数目增加，其仍会对网络产生较大的影响，当随机攻击数目340 时，网络基本无法满足正常的运行能力(E＝0.008、S＝0.203)。 ②相对于随机攻击，蓄意攻击E和S迅速地下降，呈现出先急剧下降后趋于平缓的趋势，当攻击站点数为150 时，网络接近完全瘫痪状态(E＝0.007、S＝0.098)，不足初始E和S的10%，这说明在攻击初期，移除的站点多为网络中的强度高站点或换乘站点等关键站点，对网络的整体连通性和传输效率有致命性的破坏，在攻击后期，移除的站点多为强度低的边缘站点，对网络的稳定性不会有较大的影响。 这表明在非级联失效下，网络对随机攻击具有较强的稳定性，对蓄意攻击具有脆弱性。

(2) 在级联失效下:①随机攻击与非级联失效随机攻击变化趋势相似，但其存在多个陡降现象，如当攻击站点数217→218，E和S有较大幅度的下降( ΔE＝0.018、ΔS＝0.285)，这可解释为随机攻击的站点为网络中的关键站点，从而引发多轮的负荷重分配，导致多个站点故障。 ②相对于其他攻击方式，蓄意攻击E和S下降最为急剧，仅攻击130 个站点，即可使网络接近瘫痪状态(E＝0.005、S＝0.076)。 这表明在考虑站点间的传播动力学下，级联失效对网络整体连通性和传输效率破坏更为显著。

(3) 当α＝0.2、β＝0.7 时，网络在级联失效下最多可抵挡283 次蓄意攻击、575 次随机攻击，这说明尽管该最佳容量参数组合，相比于其他容量参数组合，网络已具有较强的抗毁性，但相对于随机攻击，其仍对蓄意攻击具有脆弱性。

4 结论

文章基于复杂网络级联失效理论，构建基于非线性负荷-容量的UPTN 级联失效模型，利用该模型分别研究网络在单站点攻击和循环攻击2 种级联失效模式下的网络抗毁性，并对比有无级联失效下的网络抗毁性，得到以下主要结论:

(1) 容量参数α的减少或β的增加，对网络抵抗级联失效能力有着显著的提升；

(2) 在单站点攻击模式下，当β处于临界阈值时，小幅增加β，网络抗毁性呈现出突增现象；

(3) 在循环攻击模式下，当α ＝0.2、β＝0.7 时，网络在成本资源消耗较低的情况下，实现了较高抗毁性；

(4) 无论有无级联失效，UPTN 在蓄意攻击下均比随机攻击更具脆弱性，特别地，网络在级联失效下，其脆弱性更为明显。