应用D2Q9 格子玻尔兹曼模型研究超快激光传热过程

赵国晨孙浩森王先征于明志毛煜东

(1.山东建筑大学热能工程学院，山东 济南 250101；2.山东建筑大学学报编辑部，山东 济南 250101)

0 引言

超快激光技术因具有加热速度快、能量密度和精准性高等优点而广泛应用于激光焊接[1]、激光加工[2-3]等诸多领域。 硅薄膜是一种比较常见的半导体材料[4]，在芯片[5]、太阳能电池[6-7]和各种电子系统[8]等领域都具有十分广泛的应用。 借助超快激光加热硅薄膜探索微/纳米结构的传热过程，对于材料加工、热处理[9]以及微电子系统的散热[10]等技术具有重要的现实意义。

傅里叶定律可用来描述宏观上的传热过程，但其假设热的传播速度无限大且是以扩散的方式在材料中传播，对于超快速加热过程并不适用。 格子玻尔兹曼方法(Lattice Boltzmann Method， LBM)是玻尔兹曼输运方程(Boltzmann Transport Equation， BTE)常用的数值解法，具有计算工作量较小、边界处理简单、易于编程等优点，非常适合于求解微纳米尺度下的热输运问题。 BTE 方程具有非常复杂的碰撞项，无法对其直接求解。 1954 年，BHATNAGAR、GROSS 和KROOK在不影响求解结果的前提下引入了一个简单的碰撞算子模型简化了BTE 模型，称为LBGK 模型，成为后来LBM 的主要研究模型[11]。

硅薄膜作为半导体材料，其内部热量传递的热载子为声子[12]。 德拜模型认为所有声子都以单一、固定的速度传播，而与声子的频率无关，将所有声子分支压缩成一个线性色散关系[13]。 在遵循德拜模型假设的前提下推导出了灰色LBM 模型(Gray LBM Model)，忽略了声子特性的频率依赖性，大大简化了求解过程，因此也成为了模拟声子输运的主要模型。 文章应用灰色LBM 模型研究了超快激光加热硅薄膜的二维导热问题，探究了这种超短时间、超小尺寸的传热问题，展示了二维薄膜内部能量密度的分布情况，并对比分析了一维结果[14]。

1 理论分析

1.1 晶格模型

LBM 主要由玻尔兹曼输运方程、晶格、格点至格点的传输限制等部分组成[15]。 晶格可以描述为对研究区域的空间离散化，进而可以扩展为对速度域进行离散化，因为粒子或粒子群在LBM 中只允许沿着连接两个连续相邻节点的方向移动。 两个常用的二维晶格示意图如图1 所示。

图1 二维晶格模型示意图

D2Q5 是二维晶格中最简单的模型，其每个格点只有4 个相邻点，所以仅有4 个与之相关的离散传播速度，这还不足以代表粒子可以传播的所有可能方向。 为了取得更加精确的结果，文章选用传播速度更多的D2Q9 模型，其每个格点有8 个相邻点交换能量，可以很好地模拟二维传热问题[16]。

1.2 格点到格点的传输限制

格点到格点的传输限制迫使粒子在离散时间步长内从一个晶格位置跳到相邻晶格位置，从而有效地将格点到格点的距离d与离散时间步长dt的大小相关联，如图2 所示，其中c为离散速度。 这一限制有助于简化玻尔兹曼方程的离散推导。

图2 格点到格点的传输

1.3 控制方程的推导和离散

Boltzmann-BGK 模型的表达式由方程(1)表示为

式中f为速度分布函数；v为粒子的群速度；τ为弛豫时间(粒子发生两次碰撞的时间间隔)；ƒeq为平衡状态下的速度分布函数。

由声子能量密度表示的BTE 可由式(2)表示为

式中e为能量密度；e0为平衡能量密度；x和y为位置参数；τ0为声子弛豫时间。

文章采用的D2Q9 模型，共有9 个离散速度，控制方程可由式(3)表示为

式中i＝0，1，2，…，8 为不同的速度方向。 当i＝0 时，；当i＝1，2，3，4 时，；当i＝5，6，7，8时，

为方便计算进行下列无量纲变换，由式(4)～(6)表示为

式中x*、y*为无量纲位置参数；L、M分别为薄膜厚度方向和长度方向的特征尺寸；t*为无量纲时间参数；e*为无量纲能量密度参数；bi为不同方向的比重系数，相加和为1；E1为初始温度下的能量，E1＝e(T0)＝CvT0，其中Cv为硅的体积热容；T0为初始温度。

基于LBM 建立超快激光加热薄膜问题的二维导热模型，由式(7)表示为

式中S(x，y，t) 为激光能量的吸收率，可由式(8)表示为

式中J为激光能量的发射密度；R为表面反射率；tp为激光脉冲的持续时间；δ为激光的穿透深度；r0为激光热源影响半径。

将式(4)～(6)的无量纲变化带入式(7)，得到无量纲化后的控制方程，由式(9)～(17)表示为

离散化后的无量纲化的控制方程可以由式(18)～(26)表示为

2 方法验证

尺寸效应会对热导率产生影响，是纳米尺度传热的显著特征之一。 ALVAREZ 等[17]基于扩展的不可逆热力学，提出了一个尺寸相关的有效导热系数表达式，由式(27)表示为

式中kF为硅的体导热系数。 从表达式中可以清楚地看出有效导热系数取决于克努森数，而克努森数反映了纳米级导热系数的尺寸效应。 此外，当平均自由程远小于器件的特征长度时，有效热导率近似等于体热导率。 相反，当器件的尺寸趋于零时，克努森数趋于无穷大，有效导热系数近似线性地取决于器件的尺寸。 该模型的优点为在较大克努森数范围内的结果与实验结果一致[17]。 AMON 等[18]运用LBM 研究了纳米尺度硅薄膜中的热传输，表明硅薄膜的面外有效导热系数取决于克努森数和表面调节系数，其表达式可由式(28)表示为

式中表面调节系数α为扩散反射的热载体分数，文章取α＝1。 该模型不仅反映了尺寸效应，而且还反映了热载体在硅薄膜表面的扩散和镜面散射的影响。

将文章所研方法获得的热导率结果与ALVAREZ 等[17]、AMON 等[18]的结果进行比较，如图3 所示，在0 ～150 nm 厚度范围内，文章方法所获得的热导率与两者的结果较为吻合，尤其与ALVAREZ 等[17]的结果吻合度较高，而与AMON等[18]的结果误差最大值≤20 W/(m·K)。

图3 不同方法获得的有效导热系数对比图

3 结果与分析

3.1 超快激光加热硅薄膜厚度方向传热问题

采用绝热边界条件，涉及到的参数见表1。

表1 硅薄膜与超快激光基本参数表

为了方便与一维结果进行对比，将被激光照射后薄膜的温度分布转换为无量纲能量密度分布，结果如图4 所示，其中图4(a)～(c)为激光开始照射后不同时间的薄膜被加热中心位置的厚度方向的无量纲能量密度分布图。 超快激光在无量纲时间t*＝0 时照射薄膜一侧的中心位置，此时被加热区域的无量纲能量密度开始快速上升并且向薄膜内部传递。 在激光持续加热阶段，被加热面的无量纲能量密度快速升高，而激光对薄膜内部的影响随着厚度方向的深入逐渐减弱。 这是由于超快激光在很短的时间内将大量的能量传递到薄膜，使得薄膜靠近被加热面区域的能量密度急剧升高，此时能量在薄膜内部传递的速度远远小于激光传递给薄膜能量的速度。

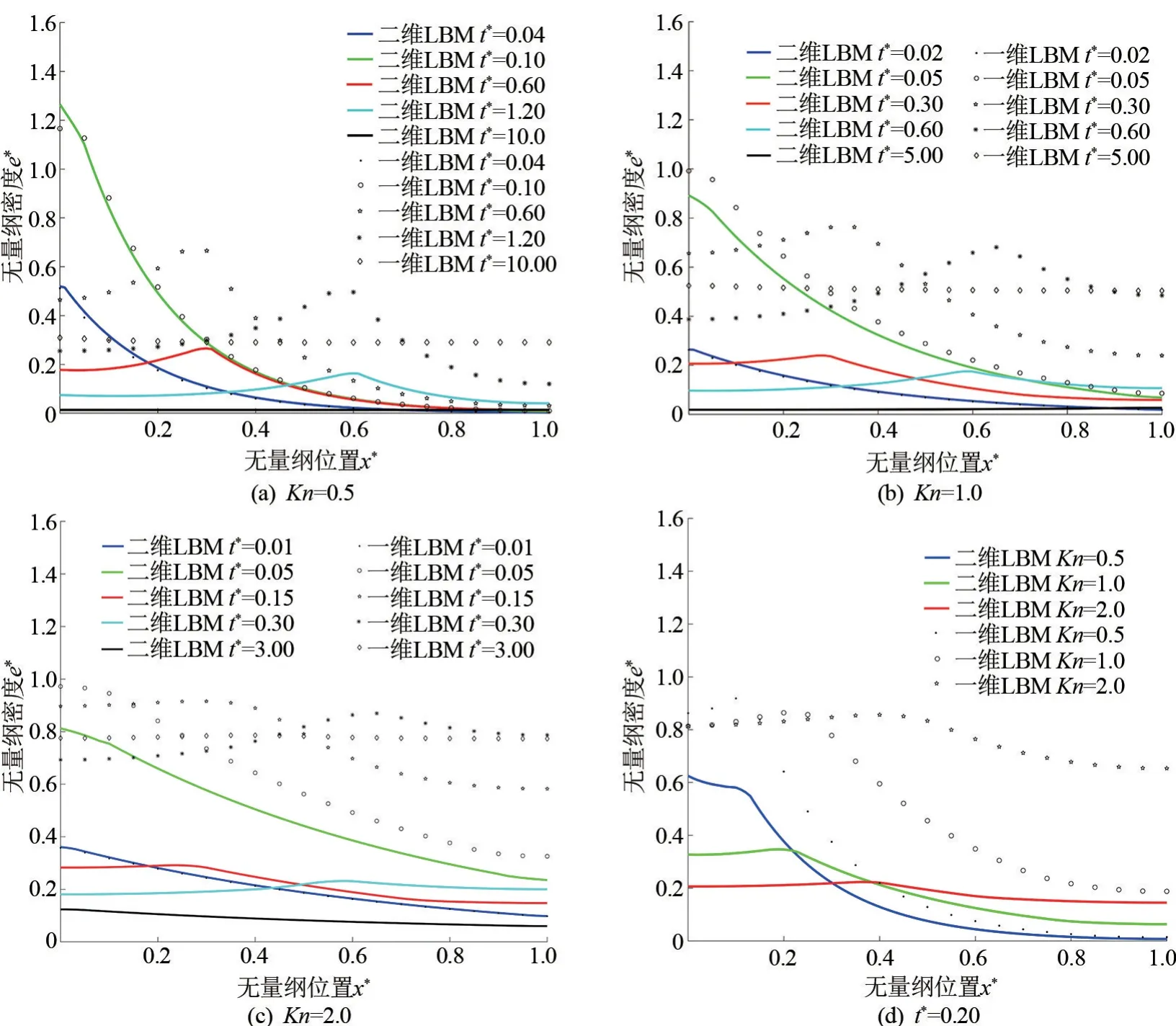
图4 硅薄膜被激光加热时厚度方向无量纲能量密度分布图

Kn＝0.5 时无量纲能量密度的分布图如图4(a)所示，此时薄膜的厚度为82 nm，固定薄膜的纵向长度为薄膜厚度的10 倍。 当无量纲时间t*为0.04、0.10时，二维LBM 与一维LBM 模拟的结果基本吻合，薄膜左侧被加热面附近区域的能量密度明显高于其他区域，且薄膜靠近右侧位置的无量纲能量密度为0，说明此时激光加热还未影响到薄膜右侧位置。 在这两个时间点时激光还处在加热薄膜阶段，被加热位置的能量密度快速上升，此时由于时间较短，激光主要作用在薄膜厚度方向，而在纵向上的能量传递较小。 激光对薄膜的穿透深度有限，加热主要作用在被穿透区域，所以在时间较短时激光对薄膜右侧不会有明显的影响。 当t*为0.60 和1.20时，可以看到能量在薄膜内部是以波的形式传递，且随着能量的传递无量纲能量密度的峰值是逐渐减小的。 此时的一维与二维模拟的结果虽然在相同时刻时在薄膜内部传递的规律及波峰出现的位置是基本相同的，但是二维LBM 模拟的无量纲密度的数值已经明显小于一维LBM 模拟的结果。 当激光开始照射薄膜后引起薄膜左侧的能量急剧升高并开始沿厚度方向和纵向传递，相对于能量的升高速度，能量的传递会有一定的迟滞，这一点是被傅里叶模型忽略的，所以能量在傅里叶模型下都是以扩散形式传递的。 由于模拟采用的是绝热边界条件，所以当激光照射结束后，能量在薄膜内部的传递是守恒的。 一维LBM 忽略了能量在薄膜纵向上的传递，能量仅在横向传递，随着时间增加，二维LBM 会有越来越多的能量传递到纵向，直到整个薄膜达到平衡。

Kn＝1.0 和2.0 时无量纲能量密度的分布分别如图4(b)和(c)所示，此时的薄膜厚度分别为41.0、20.5 nm。 随着薄膜厚度的减小，激光对薄膜厚度方向上的影响也越来越大，薄膜内部能量传递的波动性减弱，能量密度达到稳定所需的时间也越来越少。对比图4(a)～(c)发现薄膜最后达到稳定时的能量密度随着克努森数的增大而逐渐增大。 为了进一步探究克努森数对薄膜内能量密度分布的影响，模拟了t*＝0.20 时不同克努森数的薄膜被加热中心位置厚度方向的无量纲能量密度分布，如图4(d)所示。 可以看出，克努森数越大其能量密度峰值也就越大，峰值达到的无量纲位置越远。

一维LBM 与二维LBM 在不同克努森数情况下模拟的能量传递规律相同，二维LBM 考虑了能量的纵向传递，导致横向传递的能量出现大幅度的减小，说明在研究薄膜中能量的传递时不能将纵向传递忽略。

3.2 超快激光加热硅薄膜纵向传热问题

在不同t*时刻，薄膜被加热面纵向能量密度分布如图5(a)～(c)所示。 可以观察到，在激光加热阶段被加热的位置能量密度快速上升，而离加热位置较远的区域能量密度并没有明显变化，加热结束后能量随着时间逐渐向外传递，并展现出了与厚度方向上类似的波动传递的现象。 由于薄膜的纵向尺寸随厚度减小而减小，而激光加热半径不变，所以在图中可以观察到随着克努森数的增大，被加热区域占总区域的比例也逐渐增大。 无量纲能量密度在被加热的中心位置最高，并向两侧逐渐减小。 随着时间的推移能量不断向两侧传递，这一点与在厚度方向上的传递规律类似。 而相同时刻，薄膜厚度方向上的能量波动要大于纵向，在纵向上传递的能量是远小于厚度方向的，所以薄膜纵向上堆积的能量会小于厚度方向，进而造成能量波动小于厚度方向。薄膜的纵向尺寸大于厚度方向，能量密度在纵向上达到稳定需要的时间要长于厚度方向。

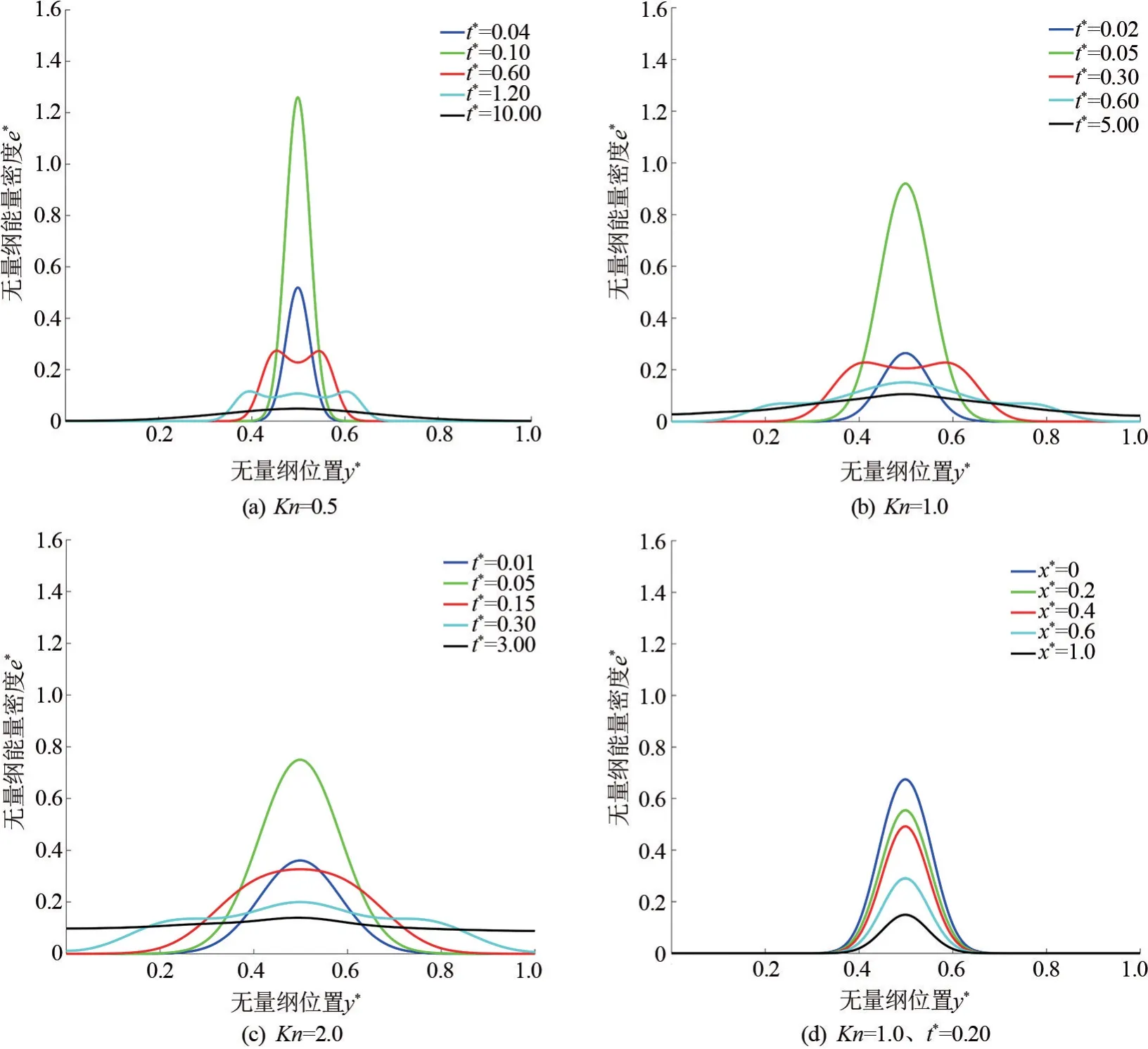
图5 硅薄膜被激光加热时纵向无量纲能量密度分布图

为了研究在某一时刻薄膜内部纵向的能量密度分布，模拟了当Kn＝1.0、t*＝0.10 时薄膜内部纵向的能量密度分布，结果如图5(d)所示。 可以看出，薄膜在这一时刻，纵向上的能量密度随薄膜厚度的深入而减小，影响范围也逐渐变小，这是因为激光对薄膜的穿透深度会沿照射中心位置向两侧逐渐变浅，携带的能量也逐渐变小。 由此可见薄膜内部纵向与厚度方向上的能量传递是会相互影响的。

4 结论

基于玻尔兹曼输运方程，采用D2Q9 的二维LBM 模型模拟了超快激光加热硅薄膜的能量传递，主要结论如下:

(1) 薄膜被激光照射后，靠近加热位置的区域能量密度快速升高，随着时间的推移，影响的区域逐渐增大。 在薄膜被加热区域附近，激光照射为能量来源，而薄膜内部的能量来源主要来自热传导。

(2) 能量在薄膜内部以波的形式传播，在厚度方向和纵向上的传递都展现出了明显的波动性，导致能量的峰值出现在了薄膜的内部，其位置会随着时间而发生改变。

(3) 虽然当激光做热源时在厚度方向上携带的能量要多于纵向，但厚度方向与纵向上的能量在薄膜内部传递时会相互影响、相互传递，会与一维的模拟结果有较大差距，所以在研究薄膜传热问题时应同时考虑厚度方向和纵向上的传递，不能简单近似为一维传热问题。