数学思想在小学数学教学中的渗透研究

孙丽梅

【摘要】新一轮课程改革重视培养小学生的思维能力，而在数学教学中渗透数学思想，则可以推进课程改革发展，提升学生的数学思维能力.通过数学思想的渗透，小学生的数学学习能力会得到较大幅度的提高.文章分析了在小学数学教学中渗透数学思想的意义，发现数学思想对学生的数学学习能产生积极影响，同时立足实际教学案例深入分析了将数学思想渗透于小学数学教学的策略，提出科学的教学建议，旨在促进学生的思维品质提升，为教师的实践探索提供思路.

【关键词】数学思想；小学数学；教学策略

数学思想是意识之中的空间形式和数量关系，指经过思维活动而产生的结果，包括但不限于类比、统计、模型、转化思想等.在小学数学教学中渗透数学思想，顺应新课程改革发展潮流，能满足学生与日俱增的数学学习需求，助力学生的思维品质提升.掌握数学思想，就是掌握数学学习的精髓.教师应在落实基础教学的同时，重视数学思想的渗透，积极优化传统的数学思维培养模式，扩大教学活动中的问题探究、实践探索的比重，拓宽思维培养的渠道，让学生真正掌握数学思想.

一、在小学数学教学中渗透数学思想的意义

（一）推进课堂教学改革

传统数学课堂教学重视知识的传递和习题讲解，意在提高学生的数学成绩，提升其学习能力.相比传统教学而言，新课程改革背景下指向数学思想的教学，能改善课堂现状，让学生主动探究问题，实现知识的建构、技能的掌握，由此推进课堂教学改革，提升教学质效.传统“知识本位”的数学教学，很难促进学生的全面发展.而重视数学思想渗透，开展“素养本位”的数学教学，能推进课堂教学改革，取得良好的教学成果.

（二）巩固数学学习基础

对小学阶段的学生而言，数学思想的渗透，可以促使其巩固数学学习基础，建构完善的基础知识体系.数学学习的本质是数学思维的构建，需要学生在脑海中形成相应知识框架，据此解决数学问题，实现能力提升目标.数学教师在教学中向学生渗透数学思想，能让学生形成对应思维意识，从本质上分析数学表象，根据教师的提示和指点，巩固数学学习基础，进而逐步完善自己的知识体系.

（三）培养学生解题能力

数学思想的渗透对学生的解题有积极影响，能助力学生深入分析问题条件，可以拓宽学生的解题路径.教师灵活运用信息化手段呈现抽象的数学思考过程，可让学生进行多角度思考，开展全方位问题探究，使不同的数学思想得到有效渗透，提升学生解决问题的能力.在教师的带领下，小学生能主动运用数学思想探究解题方法，在运用新知识解决数学问题的同时，积累丰富的解题经验，由此提升解题能力.

（四）提升学生思维品质

小学阶段学生的思维正处于起始发展阶段，其具象化思维占据主导，思维敏捷度较高，思维的跳跃性较强.在数学教学中渗透数学思想，能提升学生的思维品质.小学生对陌生事物有着强烈的好奇心，教师可利用这一点渗透数学思想，指导学生通过类比分析、统计研究、建构模型、演绎转化等方式，掌握数学思想.教师紧跟数学课程改革步伐，利用教学活动向学生渗透数学思想，能改善学生的思考习惯，使之在更高层次的学习中提升思维品质.

二、將数学思想渗透于小学数学教学的策略

（一）理清知识脉络，渗透类比思想

在小学数学教学中渗透类比思想，可以帮助学生理清知识脉络，使之建构完善的数学知识体系.类比思想指面对问题结论存在不同情况时，选择以分类讨论的方式进行研究的思想.教师应重视类比思想的渗透，引导学生分析同一问题的不同情况，使之理清知识脉络，学会运用类比思想分析、解决问题，逐步完善自己的数学知识体系.

比如，在讲解人教版小学二年级上册数学“表内乘法（二）”一课时，首先，教师可以利用对比的方式，指引学生分析7的乘法口诀表，在完成表格填制任务后，完成以下习题：

1.计算7×3，7×6，7×5，7×4.

2.背出7的乘法口诀.

3.两个星期有多少天？三个星期呢？

4.每只骆驼能运四个箱子，一支驼队有七只骆驼，三个驼队一共能运多少个箱子？

在解决以上问题后，教师指引学生制作以下表格，要求学生根据乘法口诀分类讨论与8有关的乘法问题，将自己的讨论结果填进表1中.

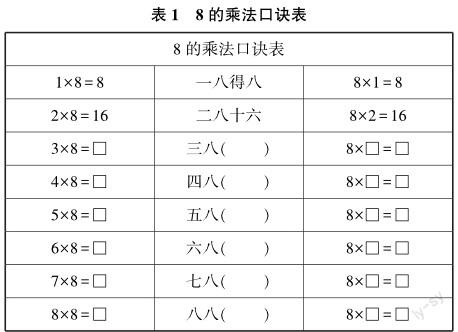
然后，教师根据学生的研究反馈，指导学生从“一一得一”背诵到“八八六十四”，总结不同计算题所用到的乘法口诀，使学生能通过分类讨论，完成表格填写任务，巩固自己的乘法口诀学习基础.为了使学生进一步理解乘法的含义，熟悉乘法各部分的名称，教师可以指引学生分类讨论7～8的乘法口诀，借此机会渗透分类讨论思想，让学生熟练进行记忆，再呈现以下示意图（如图1所示），要求学生观察并总结9的乘法口诀，分类讨论三种手势所表示的含义.

图1中的三种手势分别表示了“一九得九”“二九一十八”“三九二十七”.学生通过仔细观察上图，分类讨论三种手势，能根据乘法口诀分析用手指表示乘法关系的意义，根据弯曲的手指理解其中的道理，由此掌握分类思想，学会运用科学方法记忆和理解7～9的乘法口诀.为了巩固学生的数学学习基础，助力学生完善知识结构，教师还可以为学生提供以下例题，要求学生分类讨论结果.

例1 两个小队给花坛中的盆栽浇水.第一队中有7人，每人浇9个盆栽，第一队一共浇了多少个盆栽？第二队比第一队多浇了7个盆栽，第二队一共浇了多少个盆栽？

【问题分析】运用乘法口诀计算第一小队浇盆栽的总数，根据第一小队浇盆栽的总数，运用加法计算出第二小队浇盆栽的总数.

【分类讨论】第一小队：7×9=63（个）

第二小队：63+7=70（个）

最后，教师根据学生的分类讨论反馈，指引学生总结问题中涉及的乘法口诀，使之理清本课知识脉络，巩固自己的数学学习基础，用乘法解决简单的实际问题.

（二）开展问题探究，渗透统计思想

问题探究是一种重要的数学活动，可以拓宽数学思想的渗透渠道，便于学生掌握数学思想，高效解决数学问题，积累丰富的解题经验.统计思想是对问题整体结构进行分析，发现问题的整体结构特征，善用“集成”眼光看待整体与局部的联系，有目的、有意识地进行整体处理的思想.教师应设计符合学生认知发展规律的问题链，通过问题探究活动渗透统计思想，助力学生在解决问题中形成数学思想.

比如，在讲解人教版小学四年级上册数学“条形统计图”一课时，首先，教师可以从天气问题入手，指导学生观察以下天气情况表（如表2所示），设计对应的问题，要求学生解决问题，探究统计信息的方法.

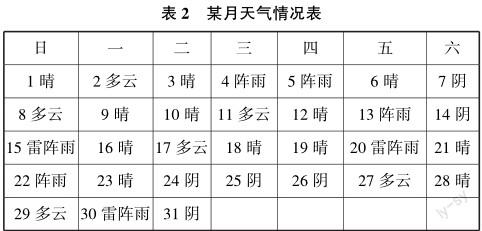
1.这个月中的不同天气分别有多少种？

2.如何用图表表示天气信息？

以上两问构成了指向统计思想培养的问题链，可以引导学生根据信息作图，部分学生选择用表格的形式总结天气信息，也有学生选择用针点图的方式集中体现天气信息.然后，教师称赞学生的独特想法，引出条形统计图的概念，根据天气情况，制作条形统计图（如图2所示），便于学生更加形象、直观地描述、分析天气数据.

借助上图分析天气信息，可以使学生明确统计图中要有标题、横轴、纵轴等要素.教师指导学生继续讨论条形统计图的画法，以“睡眠时间调查”问题为引导，要求学生思考如何集中体现班级学生睡眠总体时间，尝试研究多样性条形统计图的画法，并提出睡眠建议.在问题驱动下，学生能产生运用统计思想绘制图形的积极性，通过调查全班学生的睡眠时间，制作对应的数据表，根据数据表绘制自己喜欢的条形统计图，由此形成统计思想，经历数据收集、整理、描述、分析的过程.最后，教师根据学生的睡眠建议，提出问题：“相比单式条形统计图，复式条形统计图有什么优势？”由此启迪学生的统计思想，使之通过对比得出以下结论.

1.单式条形统计图：只能表达一种事物数量变化情况，缺少图例，不便于对比；

2.复式条形统计图：可以反映两种（以上）事物数量变化情况，有图例且便于对比.

学生通过对比两类统计图，结合天气信息、睡眠时间等数据，总结两种统计图的区别，掌握统计思想，形成了细心观察的良好品质.

（三）创设直观情境，渗透模型思想

创设直观情境是渗透数学思想的常用方法，能营造良好的情感氛围，助力学生理解抽象的数学知识，形成良好的数学思想.模型思想指采用普遍認为比较严格的数学语言描述事物，建立数学模型，用模型代替实物进行论证、研究，降低解决问题难度的思维方式.在渗透思想的同时创设情境，能取得良好的思想培养效果.教师应在教学中创设直观情境，利用直观模型指导学生分析、解决问题.

当数学问题与等式建立存在关联时，学生就可以通过列方程并求解的方式解决问题.学生通过用字母表示等量关系，对方程形成了初步认识.之后，教师就可以渗透建模思想，引导学生用方程求解以下问题.

例2 一桶蓝莓汁1200g，从桶中倒出三杯.假设每杯蓝莓汁为xg，能否用含有字母的式子表示桶中蓝莓汁的剩余量？当x=200时，蓝莓汁还剩多少？

【问题分析】根据问题明确数量关系，可知三杯蓝莓汁为“3xg”，用总的蓝莓汁重量减去三杯蓝莓汁重量便可得到带字母的等量关系式，将“x=200”代入求解便可得到问题答案.

【建模讨论】根据题意用方程表示桶中蓝莓汁的剩余量，即“（1200-3x）g”，再将“x=200”代入其中，得“1200-3x=1200-3×200=600”，可知蓝莓汁还剩600g.

在运用简易方程解题时，学生容易对抽象的等量关系式以及解方程产生困惑.对此，教师则可以利用思维导图创设直观情境，系统总结未知量、问题条件、等量关系、方程等基础知识，让学生在直观情境中借助思维导图建构概念，理解运用方程建立模型的意义，形成良好的建模思想.最后，教师出示问题，要求学生运用方程进行求解，锻炼学生的建模思维.

例3 小丁在运动会的掷铅球比赛中，以4.21m的成绩打破班级原有比赛纪录，超过纪录0.06m，尝试求出班级原纪录.

【问题分析】原纪录是未知数，将其设为xm，列方程解答即可.

【解题步骤】解：设班级原纪录为xm.

根据问题中的数量关系列方程x+0.06=4.21，

求解x+0.06-0.06=4.21-0.06，x=4.15.

答：班级原纪录为4.15m.

通过解决实际问题，学生明确了应用建模思想解决问题的步骤：找未知数、分析关系、列方程、求解、检验、作答.如此一来，学生形成了良好的建模思想，能根据实际问题列出方程并求解，切实提升思维品质.

（四）鼓励自主实践，渗透转化思想

自主实践活动可以锻炼学生的自主学习能力，教师遵循过程性原则培养学生的数学思想，能促进学生实践能力的提高.转化是将陌生、复杂问题以演绎、归纳等方式，转化为熟悉、简单问题的思维方式.教师在数学教学中应鼓励学生自主实践，为其提供不同的实践指导，科学渗透转化思想，让学生将复杂问题简化，运用转化思想探索解决问题的全新方法，提高数学学习能力.

比如，在讲解人教版小学六年级上册数学“分数除法”一课时，首先，教师引导学生复习整数除法知识，在迁移中引出分数除法课题，介绍倒数的概念，让学生明白分数的倒数，就是将分子分母互换位置得到的数.然后，教师设计“分数除法的转化”活动，要求学生按照以下方案进行自主实践，探究分数除法问题.

最后，教师鼓励学生交流例题解法，着重分析分数除法计算步骤，通过观察、类比、研究，理解倒数、分数除法算理，总结运用转化思想求解问题的方法，在知识迁移中内化分数除法计算技巧，形成自主探索和创新意识.

结束语

简而言之，在小学数学教学中渗透各类数学思想，能推进数学课堂教学改革，巩固学生的数学学习基础，让学生运用各类思想高效解决问题，不断提升其思维品质.教师在教学实践中帮助学生理清数学知识脉络，设计形式丰富的问题探究活动，将学生置于直观情境中，依托自主实践渗透类比、统计、模型、转化等思想，拓展学生的数学思维，能使其从根本上认识数学学科的本质.因此，教师应重视数学思想的渗透，运用多样化方法改变学生的思维方式，促进其思维能力提升.

【参考文献】

[1]黄俊强.归纳·推理·融合：小学数学归纳推理思想的渗透[J].新课程导学，2022（11）：96-98.

[2]黎斌.模型思想在小学数学教学中的渗透[J].小学教学参考，2022（05）：96-98.

[3]王紫琦.基于数形结合思想的小学数学教学优化路径研究[J].教师，2022（04）：39-41.

[4]李志香.转化思想在小学数学“图形与几何”教学实践中的应用研究[J].教师，2022（04）：45-47.

[5]谢惠密.浅谈小学数学教学中模型思想的渗透与培育[J].新课程导学，2021（28）：61-62.