电动静液作动器的阻尼自适应扰动主动补偿控制方法

杨荣荣, 马永杰, 付永领, 张 玲, 赵家黎, 王亚洲

(1.兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2.北京航空航天大学 机械工程及自动化学院, 北京 100191)

引言

电动静液作动器EHA是一个典型的自闭式泵控电液伺服系统,具有集成度高、功重比大、效率高和安装维护性能好的优点[1-3],广泛应用于多电飞机主飞控舵面操作系统与起落架升降系统[4-5]、机器人[6-7]、汽车主动减震装置[8-9]和注塑机[10]等领域中。但EHA是一个由机械、电气和液压系统组成的多领域系统,系统中存在着大量的不确定性(结构不确定性、参数不确定性和外部扰动),这些严重限制了EHA控制性能,为了提高EHA的控制性能,亟需一种高效和可靠的控制方法。

目前已有许多先进的控制方法被提出以提高EHA的控制性能。文献[11]提出了一种基于定量反馈理论的鲁棒控制方法,可有效提高EHA远程机械手的位置跟踪性能。为了实现非对称EHA的高精度位置控制,文献[12]提出了一种基于扩张状态观测器ESO的积分滑模反步控制方法,其中ESO来估计系统未测量状态、匹配和非匹配扰动,反步法用来对匹配和非匹配扰动进行补偿,积分滑模控制器来消除静态误差,提高系统响应能力。文献[13]提出了一种基于ESO的滑模位置跟踪控制策略,该方法能对扰动进行精确估计,对外部干扰力具有较强的鲁棒性。文献[14]提出了一种基于二自由度扰动观测器的渐近稳定控制器,以补偿摩擦和内泄漏的不利影响。文献[15]提出了一种基于误差符号鲁棒积分(Robust Integral of the Sign of Error,RISE)的复合自适应控制方法,其中利用参数自适应律处理未知参数,利用RISE抑制集总扰动对系统的影响。为了提高水下EHA的跟踪性能,文献[16]考虑了附加压力补偿器和不确定的外部载荷的影响,提出了一种基于ESO的反步控制方法。为了提高一种新型定转矩变排量泵EHA的位置跟踪性能文献[17]提出了一种反步与非线性投影相结合的自适应控制方法,文献[18]针对EHA存在油液弹性模量摄动的问题,提出了一种基于H∞混合灵敏度控制器,从而提高了EHA的位置跟踪性能和对外部干扰的鲁棒性。

扰动主动补偿控制方法ADCM是一种设计简单、高效且具有强抗扰能力的一种控制方法,近年来受到了研究者的广泛关注。该方法的设计核心是通过ESO估计不确定性并加以补偿,ESO的估计精度将直接决定ADCM的控制性能。ESO的设计阶数越高对扰动估计越准确,但过高的阶数会增加ESO对噪声的敏感度[19]。文献[20]中对EHA提出了一种ADCM,但该方法所需设计的ESO阶数较高,而且控制器中存在加速度信息,造成该控制器较难在实际中实施。本研究针对传统ADCM存在的上述问题,提出了一种基于串级扰动估计器的阻尼自适应扰动主动补偿控制方法,该方法具有以下优点:

(1) 利用奇异摄动理论对EHA的传统数学模型进行降阶处理,这样不仅降低了ESO阶数和噪声敏感度,而且在控制器设计过程中,避免了作动加速度信息的使用;

(2) 为了进一步降低ESO对噪声的敏感度,提出了一种由降阶ESO和滤波估计器FE组成的串级扰动估计器,与传统ESO的不同之处在于降阶ESO仅负责估计作动的速度信息,而滤波估计器利用其估计的速度信息进行扰动估计,这样ESO的阶数和噪声敏感度进一步降低,同时通过调节滤波估计器的滤波时间常数可实现对扰动的准确估计;

(3) 在控制器中引入阻尼自适应函数,实现了系统阻尼比由欠阻尼到过阻尼的自适应调节,可有效减小位置响应所需的调节时间。

1 EHA系统描述

1.1 EHA基本原理

EHA的基本原理图如图1所示,驱动控制器根据位置控制指令执行相应的控制算法产生驱动控制信号控制由永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)的转速和方向,继而控制可逆柱塞泵的输出流量和压力,最终使液压缸活塞产生伸缩动作,实现对负载位置、速度和方向的控制。

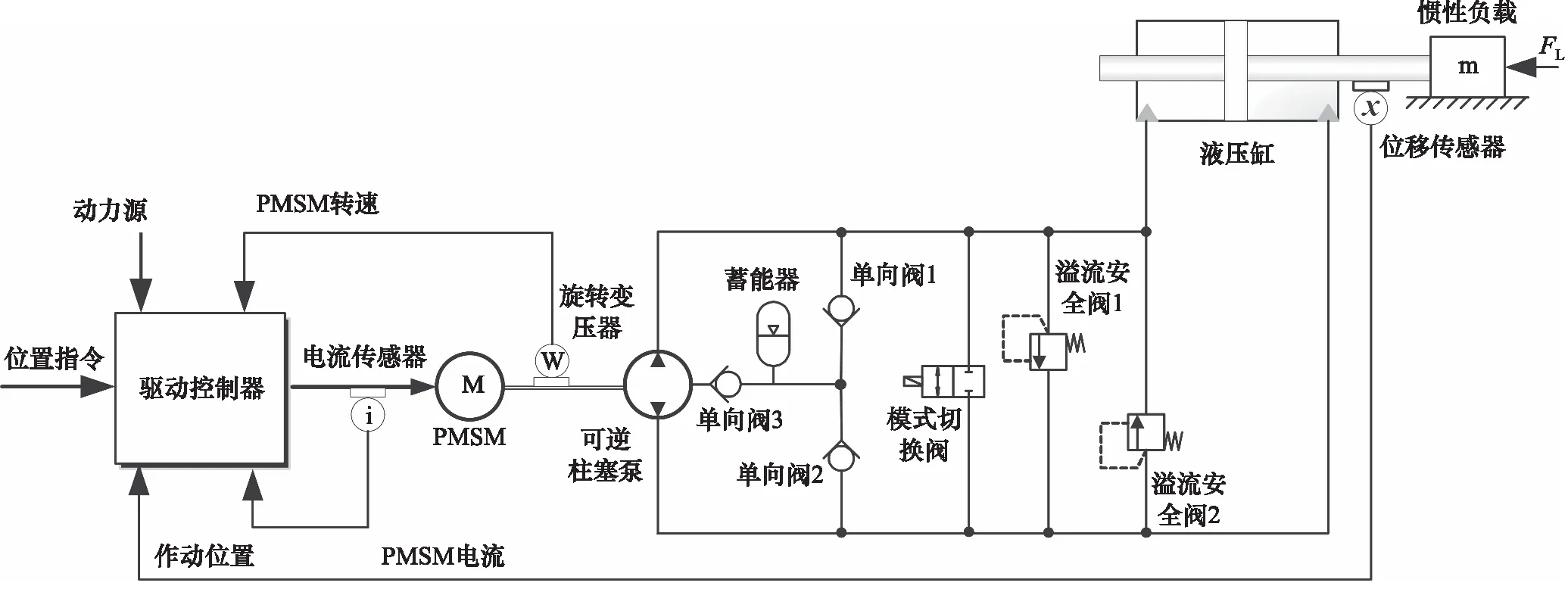
图1 EHA工作原理图Fig.1 Schematic diagram of EHA

1.2 EHA机液子系统数学模型

1) 可逆柱塞泵流量方程

对于可逆柱塞泵,流量方程可描述为:

(1)

式中,Qa,Qb—— 泵的出油口流量和进油口流量

Dp—— 可逆柱塞泵的排量

ωm—— PMSM的机械角速度

Va,Vb—— 泵出油腔和回油腔容积

βe—— 油液有效体积模量

pa,pb—— 泵的出油压力和进口压力

Qip,Qopa,Qopb—— 泵的内部泄漏流量、外部泄漏流量

2) 液压缸流量方程

忽略液压缸的外泄漏流量,则液压缸两腔的流量方程为:

(2)

式中,Q1,Q2—— 液压缸的进、出油腔流量

A—— 液压缸活塞的有效工作面积

x—— 液压缸活塞杆的位移

V10,V20—— 液压缸进、出油腔的容积

p1,p2—— 液压缸进、出油腔压力

Qic—— 液压缸内泄漏流量

3) 液压缸运动方程

由表示负载与液压缸输出力之间关系的平衡方程可得:

(3)

式中,mt—— 活塞、活塞杆和负载的总质量

Bt—— 液压缸与负载的总黏性摩擦系数

FL—— 施加在活塞杆上的外负载力

4) 压力动态方程

根据流量连续性特性,动态方程可写成:

(4)

式中,Qc1,Qc2,Qr1,Qr2—— 通过溢流阀和单向阀的流量

(5)

(6)

其中,dLm=-FL。

1.3 基于奇异摄动理论的EHA降阶模型

由式(6)可见EHA机液子系统数学模型为3阶系统,故传统ESO的设计阶数为4阶,因此ESO对噪声十分敏感。此外,由于系统中存在非匹配扰动,因此无法直接设计ADCM。尽管文献[20]中提出的ADCM利用坐标变换将非匹配扰动转换为了匹配扰动,但在ADCM中引入了对噪声有放大效应的加速度信息,造成实际难以实施。为了进一步提高ADCM的实用性,此部分利用奇异摄动理论[21]对机液子系统数学模型进行降阶处理。

(7)

令εs=0,式(7)的下式可退化为代数方程为:

(8)

(9)

(10)

设εs=0,τs=t/εs,则式(10)可转换到新的时间尺度τs框架下,则边界层模型方程可得:

(11)

很明显,边界层模型在平衡点yτ=0时是渐近稳定的。根据Tikhonov定理可知:

(12)

(13)

由式(13)可知,降阶后的系统阶数降为2阶,故ESO的设计阶数由原来的4阶降为3阶,ESO的噪声敏感度随之减弱。

2 基于滤波估计器的串级扰动估计器

为了进一步降低ESO的噪声敏感度,本节设计了一种新型的串级扰动估计器。根据系统降阶模型(13)设计ESO时,无需用ESO估计系统总扰动F(x),而是用来估计速度信息x2,这样ESO阶数进一步降为2阶,噪声敏感度大大降低。故降阶ESO可设计为:

(14)

ωox—— 降阶ESO估计带宽

(15)

式中,κ—— 低通滤波器的时间常数,κ>0

对式(13)中的第二个微分方程两边同时进行滤波,并结合式(15)可得:

(16)

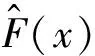
(17)

(18)

(19)

由式(19)可以得到:

(20)

3 阻尼自适应扰动主动补偿控制器设计

定义位置跟踪误差:e=xd-x1,其连续时间微分为:

(21)

因此控制量ωm可设计为:

(22)

其中,kx1和kx2>0为控制器参数。

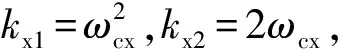
由于控制系统是一个二阶系统,因此系统特征多项式有以下对应关系:

(23)

式中,ξ—— 系统阻尼比

ωn—— 固有频率

由式(23)可知,当控制带宽确定以后,系统阻尼比ξ和固有频率ωn也就确定了,即二阶系统的响应特性也就确定了。为了进一步提高系统的响应速度,设计阻尼自适应函数f(e)来代替二阶系统阻尼比ξ,因此二阶系统的响应特性由阻尼自适应函数f(e)和固有频率ωn决定。

因此,控制量ωm最终可修正为:

(24)

其中,f(e)=(ξmax-ξmin)·e-δ|e|+ξmin,ξmin和ξmax为最小和最大阻尼比,δ为阻尼自适应敏感系数。

由阻尼自适应函数f(e)可知,当e→+∞时,f(e)→ξmin,当e→0时,f(e)→ξmax,阻尼可以实现从ξmin到ξmax的变化,因此可以实现在提高响应速度的同时保证无超调调节。整个控制器的结构框图如图2所示。

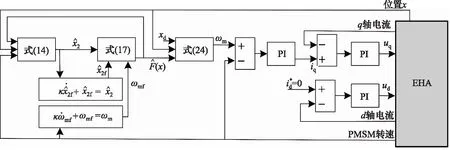
图2 系统控制框图Fig.2 System control block diagram

4 系统稳定性分析

将式(24)代入式(21)得:

(25)

(26)

如果控制带宽ωcx>1,则:

(27)

由式(27)可得:

(28)

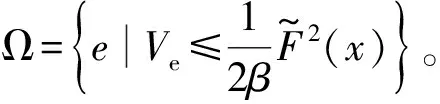
5 仿真分析

为了验证所提控制方法的有效性和控制性能,首先在MATLAB/Simulink和Simcenter/AMESim联合仿真平台上,搭建了EHA和所提控制方法的仿真模型,其中AMESim中的EHA模型如图3所示。为了使模型和仿真更加切合实际系统,在仿真模型搭建过程中考虑了液压泵的内泄漏和外泄漏,其中节流阀1用来模拟内泄漏,节流阀2、3用来模拟外泄漏,还考虑了液压缸的泄漏、死区效应、液压缸的库伦摩擦和黏性摩擦、SVPWM的死区效应。而且在FE-VD-ADCM的仿真模型中,在位置环FE-VD-ADCM、转速环PI、q轴电流环PI和d轴电流环PI的控制输出处加入了限幅非线性环节,限幅值分别为700 rad/s、16 A、300 V和220 V。然后将本研究所提控制方法与传统PI控制器和ADCM进行了比较。为了便于分析,本研究所提控制方法用FE-AD-ADCM表示。EHA系统参数如表1所示。

图3 EHA的AMESim仿真模型Fig.3 AMESim simulation model of EHA

PI控制器参数:KP=26171,KI=303670;

ADCM控制器参数:ωcx=126 rad/s,ωox=5ωcx;

FE-AD-ADCM控制器参数:ωcx=126 rad/s,ωox=5ωcx,κ=0.03,ξmax=1.2,ξmin=0.1,δ=100;

转速环和电流环均采用PI控制器,其中转速环PI控制器参数:KPω=0.05,KIω=0.3;d、q轴电流环PI控制器参数:KPi=20,KIi=2011。

5.1 阻尼自适应函数有效性分析

目标位置指令为xd=0.08 m。由图4可以看出,当FE-AD-ADCM中的ξ=0.1时, 系统处于欠阻尼状态,尽管位置阶跃响应速度很快,但出现了超调;当ξ=1.2时,系统处于过阻尼状态,尽管实现了无超调调节,但位置阶跃响应速度较慢。当ξ=f(e)时,系统处于阻尼自适应状态,在初始阶段,其响应速度与ξ=0.1时的相当;当接近目标位置时,ξ=f(e)→ξmax=1.2,系统处于过阻尼状态,此时位置阶跃响应实现了无超调调节。

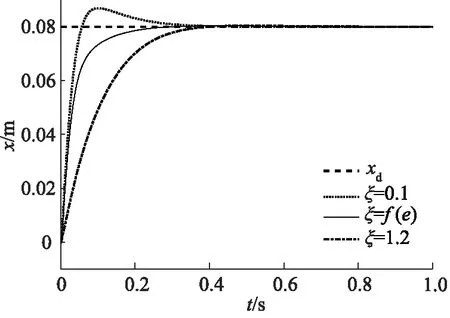
图4 xd=0.08 m时FE-AD-ADCM定阻尼和阻尼自适应位置阶跃响应对比曲线Fig.4 Position step response comparison curve of FE-AD-ADCM at constant and variable damping when xd=0.08 m

5.2 FE-AD-ADCM控制性能对比分析

考虑到实际系统中存在噪声,因此在位置信号x中加入均匀分布且幅值为1×10-4m的随机噪声信号。阶跃响应和正弦响应是实际中常见的EHA性能测试工况,因此以下分两种情况来验证控制方法对EHA的控制性能。

情况1:位置跟踪指令为xd=0.08 m。为了比较三种方法对噪声的敏感度,在位置信号x中加入均匀分布且幅值为1×10-4的噪声信号。图5为PI、ADCM和FE-AD-ADCM控制性能对比曲线,由图5a可以看出,尽管PI控制器具有最快的响应速度,但出现了38.5%的超调,而其他两种控制器均无出现超调。其次,由于FE-AD-ADCM中加入了阻尼自适应函数,系统可以实现由欠阻尼到过阻尼的自适应调节,因此其位置阶跃响应速度快于ADCM的。

图5 xd=0.08 m时PI、ADCM和FE-AD-ADCM控制性能对比曲线Fig.5 Comparison curves of PI, ADCM and FE-AD-ADCM control performance when xd =0.08 m

考虑到实际系统因工况的变化导致负载发生变化,因此在1.5 s时加入1000 N的外部扰动。从图5a可以看出,PI产生了0.0018 m的位置降,并且位置恢复时间为0.25 s。ADCM产生了0.00093 m的位置降,并且位置恢复时间为0.23 s。而FE-AD-ADCM产生了0.00026 m的位置降,并且位置恢复时间为0.23 s。由此可以看出,PI的抗扰性能最差,而FE-AD-ADCM的抗扰性能比ADCM的好,其原因是通过系统模型降阶减小了FE所需估计的扰动量,减小了FE的估计负担,因此提高了对扰动的估计精度。其中ADCM的ESO所需估计的扰动量可以计算为:F(x)=βeCt(mtV0)-1FL=-1.5×104,而FE所需估计的扰动量可以计算为:F(x)=-FL/mt= -16.7。

由图5b可以看出,PI的控制输出曲线ωm最光滑,其原因是PI控制器中仅有比例项引入噪声,并且积分项对噪声有压制作用。而FE-AD-ADCM的控制输出曲线ωm光滑度优于ADCM的,其原因是由于对系统模型降阶处理,使得FE-AD-ADCM避免了使用对噪声有放大效应的加速度信息。由图5c和图5d可以

情况2:位置跟踪指令为xd=0.001sin (4πt)m。考虑到实际系统因工况的变化导致负载发生变化,因温度的变化导致泄漏系数和黏性摩擦系数发生变化,因此在t=0 s时加入FL=500 sin(2πt)N的外部负载,同时将活塞、活塞杆与负载的总质量mt,泵和液压缸的总泄漏系数分别变成原来的两倍,泵和液压缸的总黏性摩擦系数变为原来的3倍。

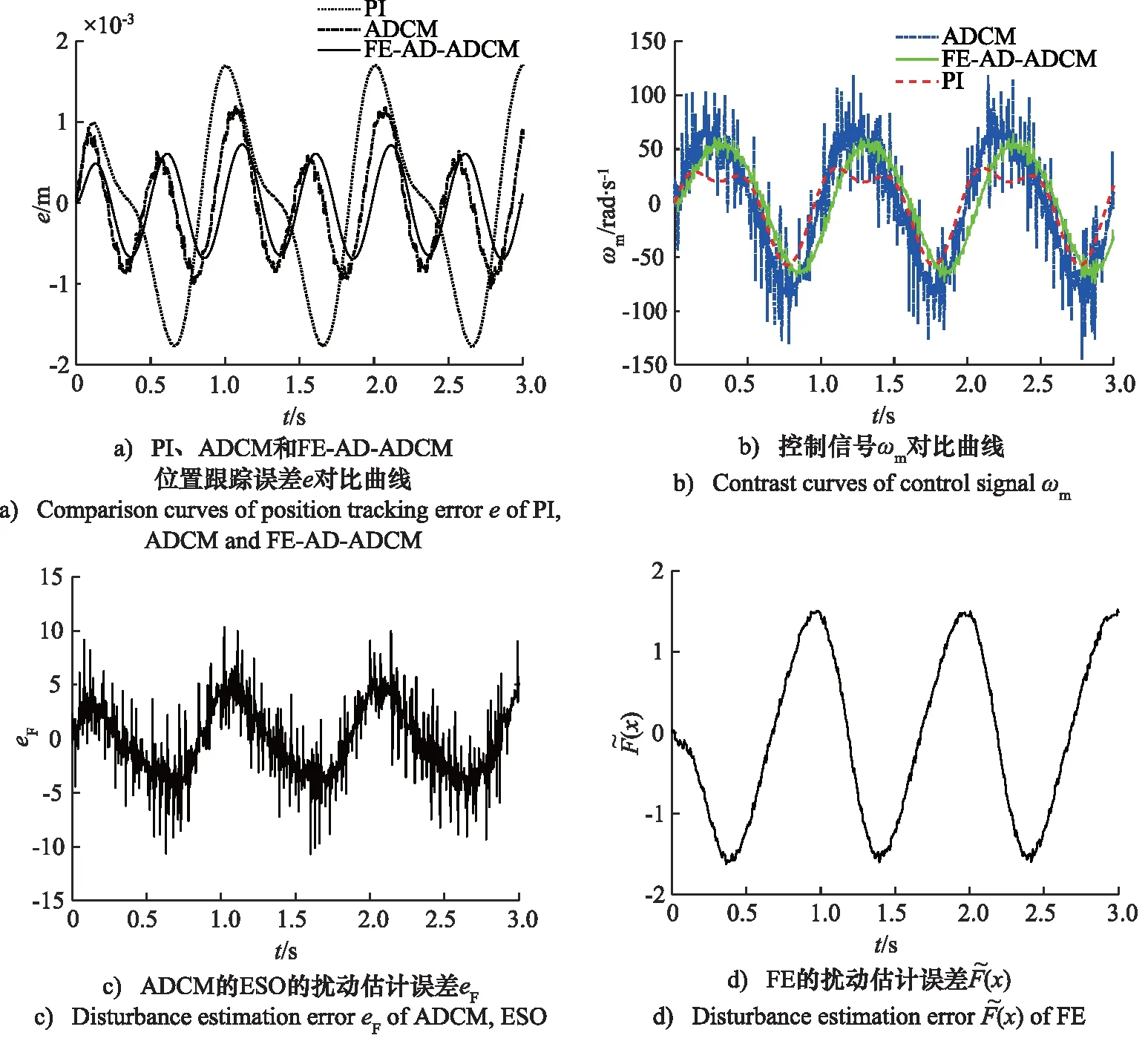
图6 xd=0.001sin(4πt)m时PI、ADCM和FE-AD-ADCM控制性能对比曲线Fig.6 Comparison curves of PI, ADCM and FE-AD-ADCM control performance when xd=0.001sin(4πt)m

6 结论

对基于奇异摄动理论的EHA降阶模型,提出了一种基于串级扰动估计器的阻尼自适应扰动主动补偿控制方法(FE-AD-ADCM),并利用MATLAB/Simulink和Simcenter/AMESim联合仿真平台,与传统PI和扰动主动补偿控制方法(ADCM)进行对比分析,仿真结论如下:

(1) 与PI和ADCM相比,由于在控制器中加入了阻尼自适应函数,FE-AD-ADCM不仅具有更快位置阶跃响应速度,而且实现了无超调调节;

(2) 与ADCM的ESO相比,由于滤波估计器FE需要估计的系统扰动量较小,因此具有更高的扰动估计精度,而且由于FE本身具有滤波功能,且估计速度信息所用的ESO经过了两次降阶,因此估计扰动信息被噪声污染的更小;

(3) 与ADCM相比,由于对系统模型利用奇异摄动理论进行了降阶处理,在控制器设计过程中避免了作动加速度信息的使用,因此FE-AD-ADCM的控制输出被噪声污染的更小。