ILC-H∞控制下车辆液压减振特性分析

伍家鸿, 曹太强, 李柏宏, 司国雷, 阳小明

(1.西华大学 电力电子节能技术与装置重点实验室, 四川 成都 610039;2.四川航天烽火伺服控制技术有限公司, 四川 成都 611130; 3.四川华能泸定水电有限公司, 四川 泸定 626100)

引言

悬架系统作为汽车底盘的关键部件之一,对汽车的整体性能具有极其重要的影响,目前悬架可分三类:被动悬架、半主动悬架以及主动悬架[1]。相较于被动悬架与主动悬架,半主动悬架因其阻尼可控且调节迅速、能耗小、成本低等优点,成为研究的热点。然而,随着汽车电子控制技术发展以及乘客对车辆舒适要求越来越高,传统的半主动悬架性能无法满足汽车在复杂路况下的行驶要求,新型半主动悬架正逐步代替传统控制的半主动悬架[2]。

半主动控制算法是半主动悬架系统控制中的关键一环。近年来,国内外学者针对汽车半主动悬架的控制策略进行了大量研究。李杰等[3-4]将Bingham模型与Bouc Wen模型应用于半主动悬架的建模优化,但对阻尼力的验证也仅仅局限于仿真。纪仁杰等[5]在悬架系统的力学模型基础上结合Lyapunov-Krasovski泛函和自由权矩阵法,证明了H∞ 控制能够有效抑制簧载加速度变化。刘尚鸿等[6-7]采用的电磁阀式阻尼可调减振器,按照复原和压缩行程分别建立了减振器动力学模型,但是在复杂工况下达不到理想的优化效果。文献[8]针对悬架系统的综合性能,基于多目标遗传算法的比例积分微分控制(Proportional Integral Derivative,PID),在传统控制基础上改善了悬架系统的减振效果。随着控制理论的研究和发展,悬架系统自身模型的不确定问题以及控制方法的局限,使得单一控制策略下的多变量控制结果并非最优解,悬架最终性能也并不符合预期[9]。

针对上述问题,本研究利用Sigmoid力学模型对ADS阻尼力进行辨识拟合,建立半主动悬架1/4车模型,采用迭代学习改进的H∞控制(ILC-H∞)方法。理论分析、仿真和试验表明:相较于传统H∞控制,新的控制策略可以降低实际路况下的不确定干扰并减小模型误差,将复杂的悬架系统模型简单化,结合两种控制策略的优势,实现车辆对阻尼参数的自动调节,提高控制的有效性和快速性。

1 半主动悬架系统建模

1.1 ADS变阻尼器力学模型

ADS阀芯开度由电磁阀进行调节,减振器在压缩和复原过程中,其两端产生的压差使油液通过阀芯阻尼缝隙,若给电磁阀通电,则会改变减振器内阻尼缝隙所产生的阻尼力,从而实现变阻尼,故可通过改变电流大小实现阻尼连续调节[10]。图1为ADS减振器实物图。

图1 ADS减振器实物图Fig.1 ADS damper physical picture

ADS减振器性能测试系统如图2所示,力学与高速耐久测试包括了减振器示功特性测试、速度特性测试。系统主要由电脑控制系统(控制上位机等)、压力传感器、显示器、液压支柱等组成。利用正弦激励,测试不同电流作用下的位移、激振速度以及相关力值。其中电流值设在0～2.0 A区间测试, 速度值0.05～1.2 m/s区间测试。具体测试值如表1所示。

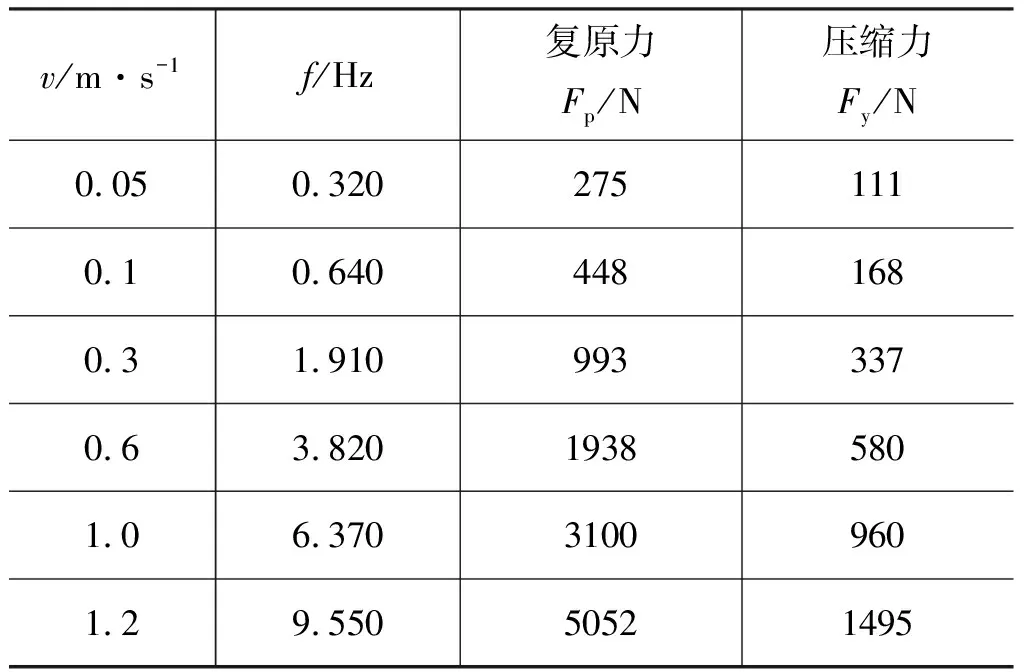
表1 减振器阻尼力试验测试值Tab.1 Damping force test value of shock absorber

图2 力学与高速耐久试验Fig.2 Mechanical and high-speed endurance test

由于Bingham模型函数具有不连续性,无法准确表示阻尼力变化情况[11]。而Sigmoid函数曲线与ADS阻尼力特性极为相似,所以利用Sigmoid模型来构建ADS力学模型。

(1)

式中,f0—— 偏置力

k—— 阻尼曲线斜率调节系数

Fb—— 控制阀输出力

α—— 阀芯开度调节系数

c0—— 阻尼系数

在此试验基础上,利用最小二乘法对Sigmoid模型进行参数辨识[12]。辨识结果如表2所示,并由图3、图4曲线拟合结果可发现:ADS的阻尼力随电流的增加而不断增大,二者具有线性关系。

表2 减振器参数辨识结果Tab.2 Result of shock absorber parameter identification

图3 控制阀输出力Fb拟合曲线Fig.3 Control valve output force Fb fitting curve

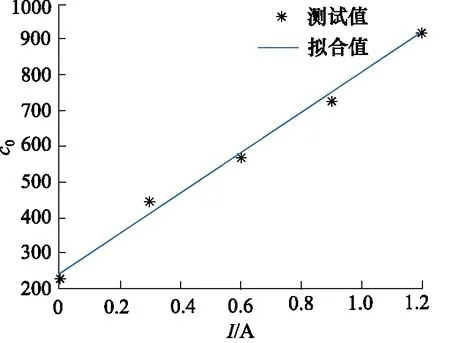
图4 阻尼系数c0拟合曲线Fig.4 Fitting curve of damping coefficient c0

结合辨识结果,考虑到k,α,f0变化并不明显,故可将三者设为常数,建立线性回归方程如下:

(2)

其中,I为电流,m1=150,m2=564.6,h1=61.1,h2=242.8,均为ADS输出力与阻尼系数的拟合系数[13]。

联立式(1)、式(2)联合可得Sigmoid数学表达式:

(3)

如图5所示为减振器示功特性曲线,x为活塞杆位移,mm;F为减振器阻尼力,N。如图6、 图7所示为减振器“阻尼力-电流-速度”特性曲线[14]。结果表明:ADS减振器可实现阻尼力0～5000 N之间随控制要求变化,在低电流状态,减振器压缩力值在1000 N左右;车辆对于路面激励和冲击的响应较快,复原力值>1800 N,相对于传统减振器,复原压缩比接近于2,对振动的抑制效果显著。

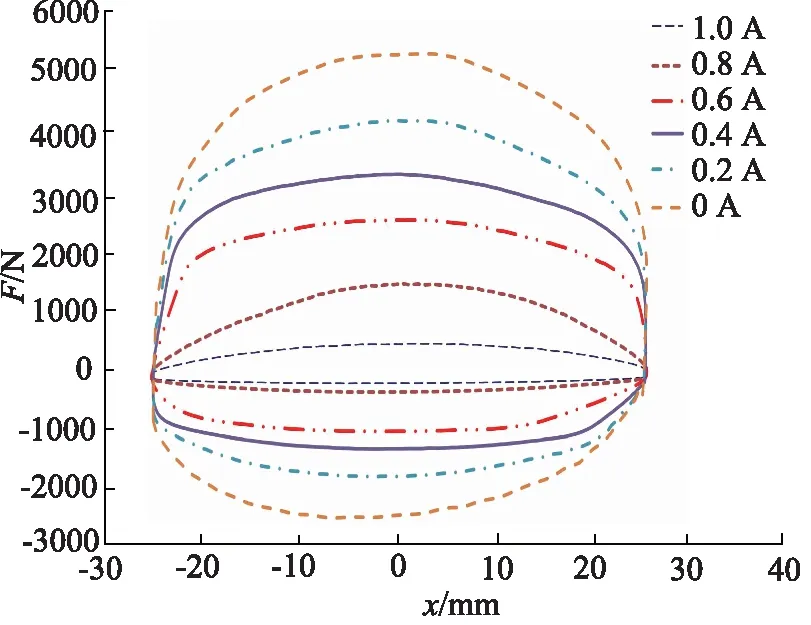
图5 减振器示功特性曲线Fig.5 Shock absorber indicator characteristic curve

图6 减振器阻尼力-速度曲线Fig.6 Damping force-velocity curve of shock absorber

图7 减振器阻尼力-电流曲线Fig.7 Shock absorber damping force-current curve

1.2 1/4半主动悬架模型

在考虑车体和车轮垂直方向受力平衡的基础上,根据牛顿第二定律,建立如图8所示的1/4车辆2自由度半主动悬架模型:

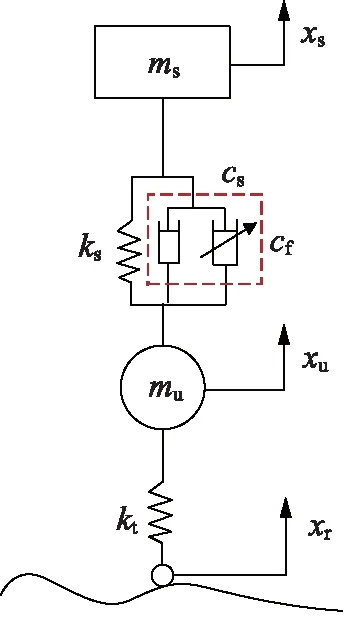
图8 1/4车辆2自由度半主动悬架系统模型Fig.8 Vibration model of 2 DOF semi-active suspension system of 1/4 vehicle

(4)

式中,ms—— 簧上质量,kg

mu—— 簧下质量,kg

ks—— 悬架螺旋弹簧刚度,N/m

kt—— 车轮刚度,N/m

xs—— 车簧上质量垂向位移,m

xu—— 簧下质量垂向位移,m

xr—— 路面激励位移,m

cs—— 半主动悬架系统的实时阻尼系数,

N·s/m

ADS减振器输出阻尼力Ff可整理为:

(5)

cf—— 半主动悬架系统的可调阻尼系数,

N·s/m

半主动悬架系统的实时阻尼系数cs和实时输出阻尼力Fs整理为:

(6)

式中,c0—— 半主动悬架系统阻尼系数,N·s/m

Fs—— 半主动悬架系统输出阻尼力,N

当车体与车轮朝着相反且向外的方向运动时,其输出阻尼力Fs为正。可得悬架系统动力学表达式:

(7)

(8)

式中,U—— 半主动悬架的阻尼控制输入向量,且有U=[Fr…xr]T,即为ADS减振器阻尼力和路面激励共同组成的矩阵

xsu—— 悬架动扰度,mm

ktxru—— 轮胎动荷载,N

As—— 半主动悬架系统矩阵

Bs—— 半主动悬架控制矩阵

Cs—— 半主动悬架输出矩阵

Ds—— 半主动悬架传递矩阵

表示如下:

将悬架系统的期望输出阻尼、位移以及振动速度作为式(3)的输入,便可计算出ADS输出电流,并将该电流作为ADS正模型的输入,实现ADS减振器在半主动悬架仿真。

2 基于ILC改进的H∞控制器设计

2.1 ILC控制器设计

图9为迭代学习控制原理,控制过程中在减小误差的同时,并且能够快速收敛,因此该控制方法结合鲁棒控制法可提高系统的稳定性和有效性。

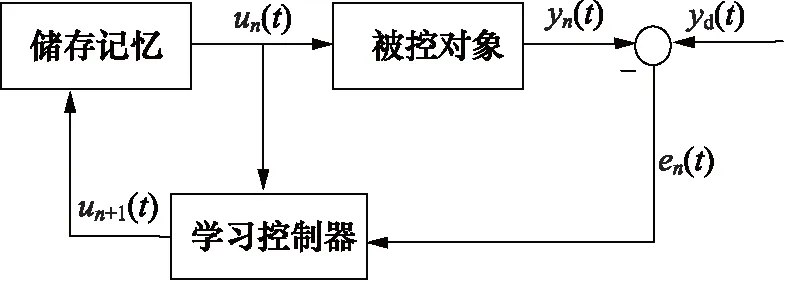
图9 迭代学习控制原理图Fig.9 Schematic diagram of iterative learning control

实际控制过程中,通过多次迭代而寻找理想的输入,并通过迭代学习率优化,而得到满足期望的控制器输出,并满足:

(9)

式中,yd(t) —— 期望输出

yn(t) —— 控制输出

由式(8)转换可得半主动悬架状态空间表达式:

(10)

式中,t∈[0,T];

xn(t)∈Rm—— 状态向量

un(t)∈Rr—— 系统输入

yn(t)∈Rk—— 系统的输出

n—— 迭代的次数

利用迭代学习律对上式整理得:

un+1(t)=un(t)+CILCen(t)

(11)

式中,en(t) —— 系统第n次的输出误差

CILC—— 学习增益矩阵

引理1 上述ILC系统满足下列要求(1)和(2)时,在区间[0,T]上,当n→∞时,en(t)→0成立:

(1) ‖I-DCILC‖<1

(2)xn(0)=xd(0)

证明如下:存在期望被控输入ud(t)使系统满足以下等式:

设在迭代过程中,初始状态xn(0)=xd(0)(n=0,1,2……),则存在:

则第n次运行时系统的输出误差可表示为:

en(t)=yd(t)-yn(t)

(12)

存在:

en+1(t)-en(t)=-[yn+1(t)-yn(t)]

=(I-DCILC)en(t)-

上式表示第n+1次与第n次输出误差之间的差值,并对其取范数:

‖en+1(t)‖≤‖I-DCILC‖‖en(t)‖+

≤‖I-DCILC‖‖en(t)‖+

经过变换可得:

‖en(t)‖λ

(13)

由于汽车运行过程中各部件的7自由度运行状态不可能测量得到,所以对汽车系统来说,首先涉及出状态观测其来估计汽车运行过程中不可测的状态x,同时考虑测量噪声v,由式(11)推导可得汽车系统模型表达式:

(14)

则H∞控制器满足:

(15)

L—— 观测器增益矩阵

K—— 反馈控制器增益

同时观测器增益矩阵L满足:

(16)

汽车系统可改写为以下形式表示:

(17)

为使扰动得到抑制,闭环传递函数Twy(s)应满足以下不等式条件:

‖Twy(s)‖∞≜‖(C+DsK)[sI-(A+BsK)]-1B1+D1‖∞

<γ

(18)

式中,γ—— 干扰衰减水平的正定标量

2.2 ILC改进H∞控制器设计

ILC改进H∞回路成形控制器可满足自身回路函数与期望值相等[15]。在系统设计满足要求的情况下,检验控制器的好坏可通过期望回路函数与控制器对应回路函数的误差来验证,即:

L(s)=K(s)G(s)

(19)

如图10所示ILC改进的H∞控制原理推导出迭代学习更新律:

图10 基于ILC改进的H∞控制图Fig.10 Improved H∞ control chart based on ILC

Kn+1=Kn+CILC(LD-Ln)=Kn+CILCen

(20)

由表3可知:随着迭代次数增加,当控制器回路函数与期望回路函数之间差值趋近于0时,即‖LD-Ln‖2→0,Kn满足ILC改进H∞回路成形控制器设计要求[16]。

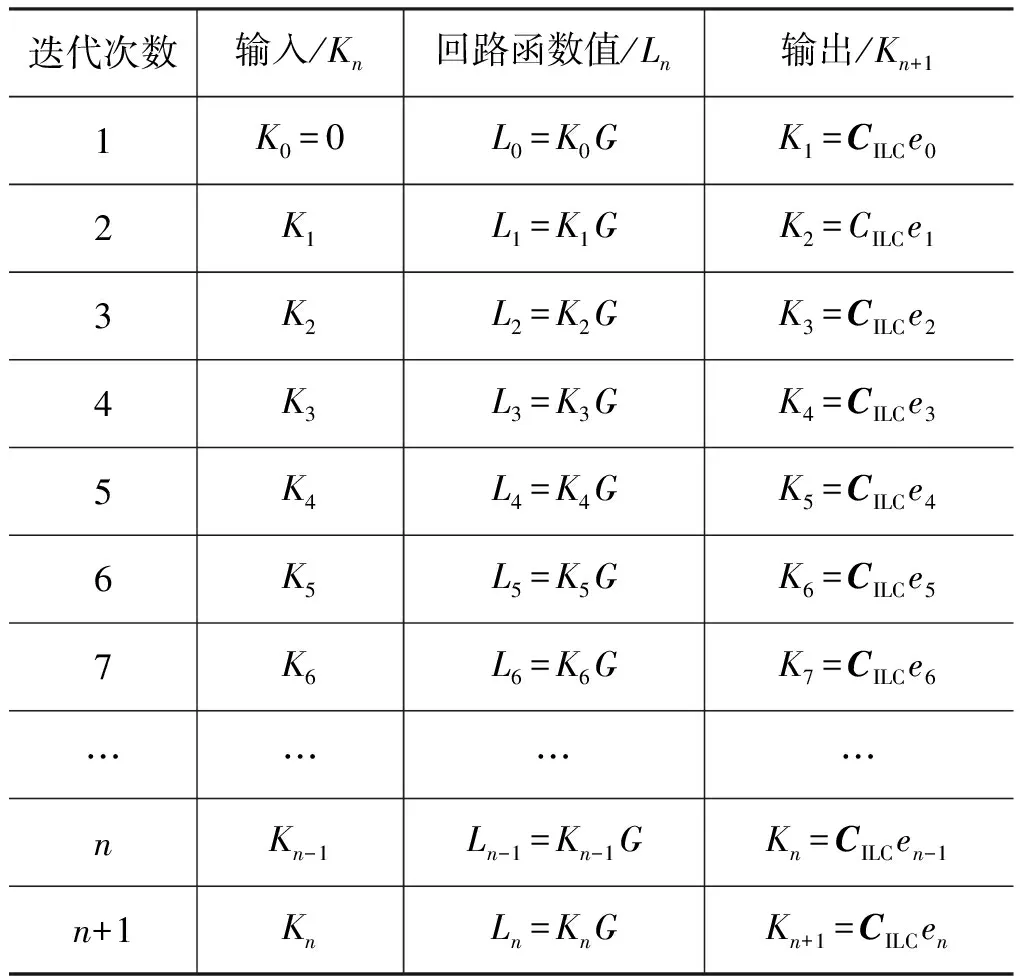
表3 迭代学习更新律表Tab.3 Law table is updated by iterative learning

表4 仿真参数数值表Tab.4 Numerical Table of simulation parameters

3 仿真与试验分析

3.1 随机路面验证

为验证ILC改进H∞控制方法对汽车半主动悬架系统振动的优化效果, 分别以B级随机路面与冲击路面作为激励搭建了MATLAB与AMESim的联合仿真,同时以原车PID控制,传统H∞控制作为参照进行比对分析,1/4半主动悬架仿真参数如表所示。

3.2 B级路面试验验证

建立B级路面不平度时域模型,且在实际中,当车速为v的情况下,路面不平度时域模型可表示为[17]:

(21)

式中,n1—— 路面不平度下,截止空间频率,

n1=0.001 m-1

Gp(n0) —— 路面不平度系数,m3

n—— 空间频率,m-1

n0—— 参考空间频率,n0=0.1 m-1

k—— 频率指数

对比H∞控制,半主动悬架系统在ILC改进H∞控制下,汽车的平顺性和振动抑制效果得到显著提升。如图11、图12所示,汽车动挠度和车身加速度分别降低了16.81%和28.74%。由图13可知,ILC改进H∞控制和传统H∞控制在对悬架动行程的抑制效果明显,尤其在高频段其抑制效果明显优于PID控制与H∞控制。由图14可看出ILC改进H∞控制和H∞控制在中频区和高频区极大地提高了舒适度。

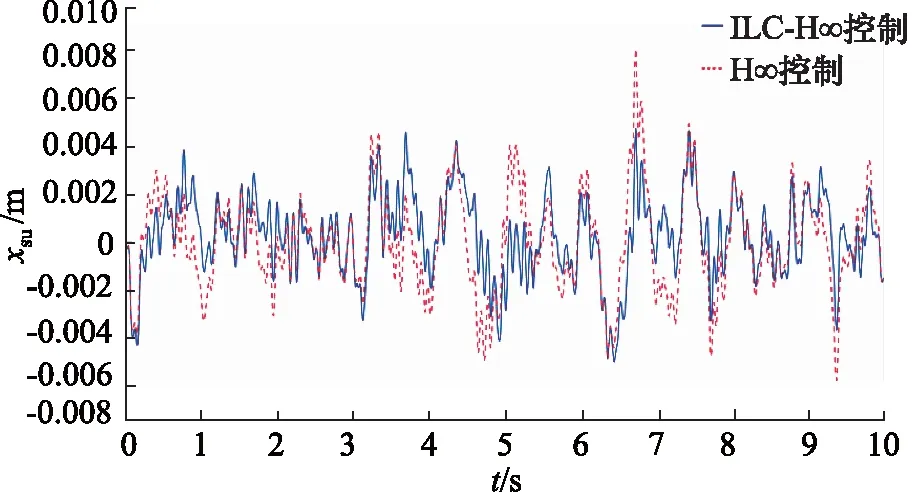
图11 悬架动扰度Fig.11 Suspension dynamic disturbance

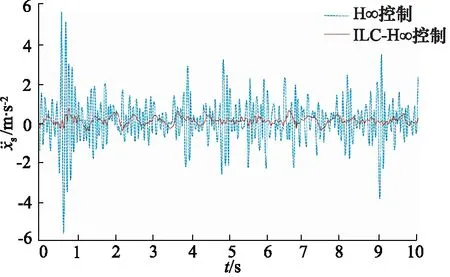
图12 车身加速度Fig.12 Body acceleration

图13 悬架动扰度功率对比Fig.13 Dynamic travel power comparison of suspension

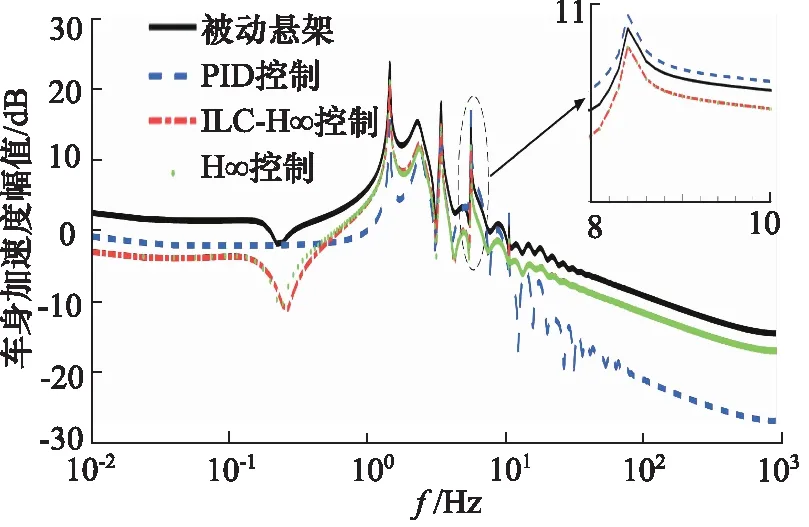
图14 车身加速度功率对比Fig.14 Body acceleration power comparison

3.3 冲击路面动态响应验证

由图15、图16车身振动FFT值分析可知:在冲击路面激励下,车身主要振动集中在0～20 Hz范围内,其中最大振动在1.5 Hz附近,为车辆的固有频率。对比ADS控制系统两种控制模式可以发现,原车H∞控制下固有频率振动幅值在95左右,其余次高级振动幅值(10 Hz附近)在50左右,两者均为低频振动,高频部分(>20 Hz)振动幅值在20以下。通过H∞控制策略介入,固有频率振动幅值被抑制在了60以下(抑制效果提升36.8%),次高级振动幅值被抑制在35左右(抑制效果提升30%)。结合图17、图18可以得:ILC改进H∞控制下的半主动悬架的各项响应振荡峰值抑制效果明显,对比H∞控制和被动悬架,其减振效果优化明显。

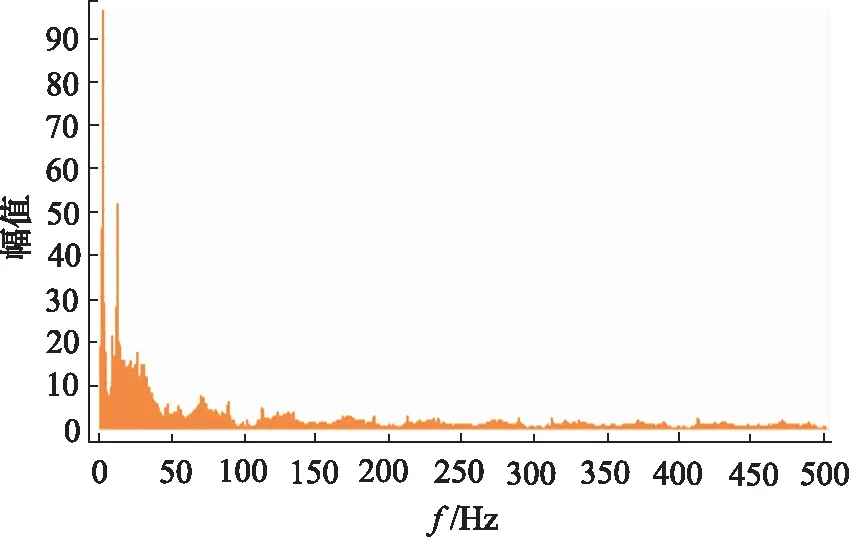
图15 H∞控制下车身振动FFT值分析Fig.15 Analysis of body vibration FFT values under H∞ control

图16 ILC改进H∞控制车身振动FFT值分析Fig.16 Semi-active ILC improved H∞ control of body vibration FFT value analysis

图17 悬架动行程动态响应Fig.17 Dynamic response of suspension in dynamic

图18 车身加速度动态响应Fig.18 Dynamic response of body acceleration

与被动悬架相比,H∞控制、ILC改进H∞控制的半主动悬架的车身加速度、悬架动行程和簧载速度性能指标提升百分比如图19所示,H∞控制、ILC-H∞控制的半主动悬架性能提升比较大,其中车身加速度上分别提升了19.8%和24.36%;而在悬架动行程上分别提高21.84%和24.68%;受悬架弹簧刚度以及固定阻尼器件影响,簧载速度性能指标提升两者差距不大,分别为21.88%和22.32%, 但是ADS可以控制低频的晃动,能量的消失可以稍微减缓。综上所述,ILC改进H∞控制系统的性能明显优于H∞控制。

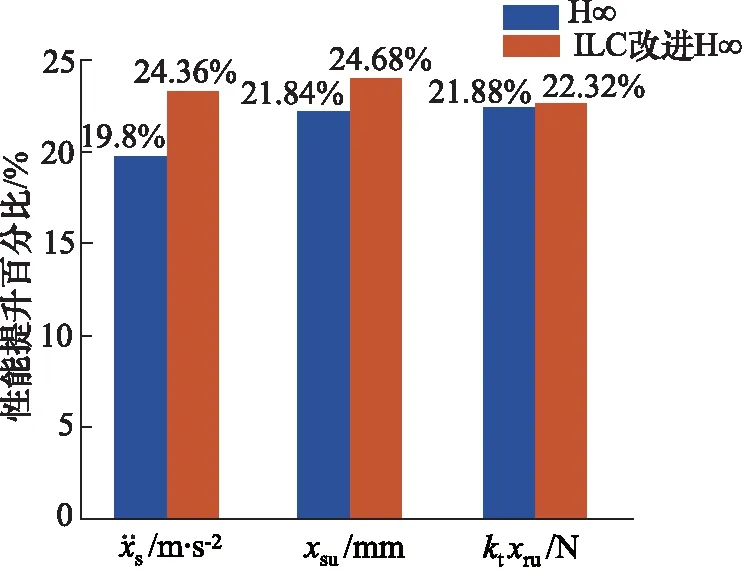
图19 各性能指标均方根值提升百分比Fig.19 Percentage increase in root mean square of all performance indicators

4 结论

针对半主动悬架系统的ILC改进H∞控制问题进行了研究,通过理论与试验验证,主要结论如下:

(1) 结合Sigmoid力学模型对ADS阻尼力进行辨识拟合,建立了减振器以及汽车1/4半主动悬架非线性动力学模型,通过搭建平台试验,并对比传统减振器,ADS对振动的抑制效果显著,复原压缩比提高近两倍;

(2) 利用迭代学习律,设计出半主动悬架ICL(迭代学习)控制器,通过引理证明和公式推导证明经过多次迭代后的误差范数,并在不同工况环境下测验,采用ILC改进H∞控制悬架系统能够将汽车动挠度和车身加速度分别降低16.81%、28.74%,同时对振动幅值效果抑制比提高近36%;

(3) 在系统满足理论设计要求的前提下,将期望回路函数与控制器对应回路函数的误差进行验证,结果表明:ILC-H∞控制器对汽车半主动悬架系统控制效果更优,该控制方式下的半主动悬架可以很少牺牲轮胎动荷载指标以及悬架动行程指标,从而大幅度控制中高频的晃动。相较于H∞控制,其车身加速度以及悬架动行程指标提升分别为24.36%,24.68%,综合性能提升近49.04%,汽车的平顺性和振动抑制效果得到显著提升。