BP神经网络优化参数的螺杆点胶阀无模型自适应控制技术

朱燕飞, 楚友洋, 李传江

(上海师范大学 信息与机电工程学院, 上海 奉贤 201400)

引言

螺杆点胶阀相较于气动点胶阀,控制精度高、出胶均匀、响应快,已广泛应用于精密点胶领域[1]。点胶阀内部的执行机构,普遍采用直流有刷电机和直流无刷电机,直流电机有刷相比于直流无刷电机,其驱动控制简单,转矩电流比大,性价比高[2]。因此,研究对象为以直流有刷电机为执行机构的螺杆点胶阀。螺杆点胶阀在用于点胶时,有两个重要指标:出胶速度和出胶量。电机转速决定出胶速度:胶体在由密封外壳和螺杆组成的密封腔内,在一定供气压力下,由电机转动带动螺杆转动将胶液挤出。电机转速越快, 其出胶速度越快。电机转动的位置决定出胶量:转动位置越大,出胶量越多。而出胶速度是否稳定,影响点胶胶粒形状是否圆润;出胶量影响胶粒质量是否均匀,这是点胶质量的最基本指标。同时,出胶速度和出胶量的精度对于整个系统的标定工作也是十分重要的。因此在螺杆点胶阀系统中,电机转速和位置的控制精度是十 分重要的。针对外部干扰和负载扰动对电机速度的影响,研究了螺杆点胶阀电机速度控制算法,不涉及位置控制的研究。

目前,螺杆点胶阀大多仍使用PID控制器,需要调参人员具有一定调参经验。在负载变化特别大时,一套PID参数往往不能满足系统的快速性和稳定性要求,且电机速度易受外部干扰和负载扰动的影响,对生产效率和质量造成较大影响。其中外部干扰主要来源为电磁、信号干扰和电源电压波动等;负载扰动主要原因为胶体为流体且部分胶体类型具有研磨颗粒,为非恒定负载,出胶针头处清理不干净容易造成堵塞引起负载较大波动。外部干扰和负载扰动一般是非周期性和不确定性的。因此,需要研究在负载变化及扰动的工况下,有更好鲁棒性的控制算法。近年来国内外对螺杆点胶阀的研究主要是针对阀体结构、流体特性分析,电机转速、供气压力对出胶量的影响等[3-5]。而对螺杆点胶阀的控制算法的研究,主要集中在直流电机的控制。刘延飞将改进遗传算法用于PID参数整定,提升了有刷直流电机动态性能[6]。刘冠艳将模糊PID用于直流电机调速,提高了抗干扰能力和稳态精度,减小了超调量,缩短了调节时间[7]。顾万里针对直流电机低速受摩擦及负载干扰影响稳态精度差的问题,设计了自适应滑模控制器,有效降低了抖振[8]。螺杆点胶阀目前大多仍采用PID控制的电流转速双闭环控制,其控制简单,易于实现,电流环可直接控制转矩。本研究采用的BP神经网络-无模型自适应控制算法无需人工整定控制器参数,对外部干扰和负载扰动也有不错的抗扰性能。

无模型自适应控制(MFAC)算法是一种无需系统精确模型的数据驱动算法,在非线性系统控制中,能实现系统的参数和结构自适应[9],目前已广泛应用到多种电机领域[10-11]。采用MFAC算法,但其调参想要达到最好的性能,也有一定难度。在MFAC参数调整的方法研究上,主要有传统的整定方法如:虚拟参考反馈整定伪偏导数[12],迭代反馈整定步长因子[13]。此外,采用神经网络来调整参数也成为研究的热点,WANG等[14]提出采用RBF径向基神经网络在线调整伪偏导数,也取得很好的性能。冯增喜等[15],费盛等[16]对电机等系统采用遗传算法对控制器参数和初值寻优,在超调和抑制调节过程振荡上有明显改善。杨龙飞等[17]针对倾旋翼飞机系统采用粒子群算法对MFAC中的参数和初值进行寻优,能够实现飞机过渡段的平稳飞行。杨延西等[18]采用粒子群算法得到改进的MFAC控制器最优参数,实现了具有较强抗外部干扰的锅炉温度控制。王华秋等[19]对变风量系统采用粒子群结合磷虾群的混合算法优化参数,获得了更快的响应时间并大幅减少超调量。

1 螺杆点胶阀电机数学模型

1.1 螺杆点胶阀原理及结构图

Psv-flow600螺杆点胶阀整体结构简图如图1所示。工作原理为:螺杆点胶阀整体由控制箱和外部气源控制,控制箱可以调节供料压力,以及驱动电机。供胶料筒1中的胶体在气源供料压力下,通过进料口2进入阀体,此时若驱动直流微电机4正转,经过减速器5减速后带动偏心螺杆6旋转,编码器7作为速度和位置的反馈装置。螺杆旋转带动胶体在螺杆和定子3组成的密封腔内运动,从而将胶体挤出到基板上。为了避免胶粒拉丝及针头残留胶液滴漏,在正转结束,胶体挤出后,再令电机反转一段行程,以扯断胶体,并回吸漏液。其本质是控制直流有刷电机转速和位置达到较高精度,才能保证点胶的效率和质量达到生产要求。

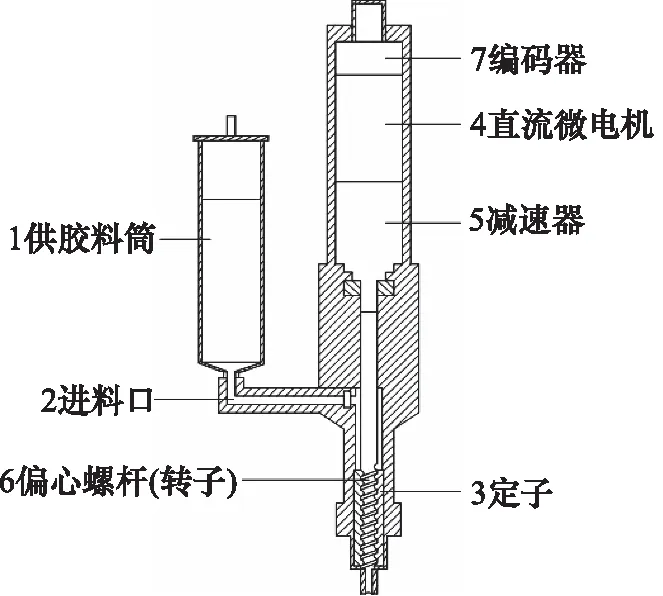
图1 螺杆点胶阀结构图Fig.1 Screw dispensing valve structural diagram

1.2 直流有刷电机数学模型

螺杆点胶阀的控制对象是直流有刷电机。采用faulhaber 24 V直流碳刷电机,额定转速6470 r/min。装配行星减速箱后,可降低转速,增大转矩,增强其稳定性。其工作原理为在电机两端施加幅值为24 V,占空比可调的PWM波,通过调节占空比改变加在电机两端平均电压值调节其转速。忽略电机黏性摩擦与弹性转矩等,其数学模型为[20]:

(1)

式中,L—— 电机电感

Ra—— 电机总电阻

Ia—— 电枢电流

E—— 反电动势

Ud—— 电枢两端电压

n—— 电机转速

CeΦ—— 电动势系数

CTΦ—— 转矩系数

Te—— 电磁转矩

TL—— 负载转矩

GD2—— 转动惯量

令负载转矩TL为0,经拉普拉斯变换,得到空载状态下电机输入直流电压Ud到输出转速n的传递函数为:

(2)

式中,Tm—— 机电时间常数

Tl—— 电磁时间常数

由于使用PWM调制来驱动电机,需要用到MOS管等电力电子器件,考虑整体的电力电子传函约为:

(3)

式中,Ks—— PWM变换器电压放大系数

Ts—— MOS管滞后时间常数。

电机环节(2)和PWM变换器环节(3)串联在闭环调速系统中。电机参数如表1所示。

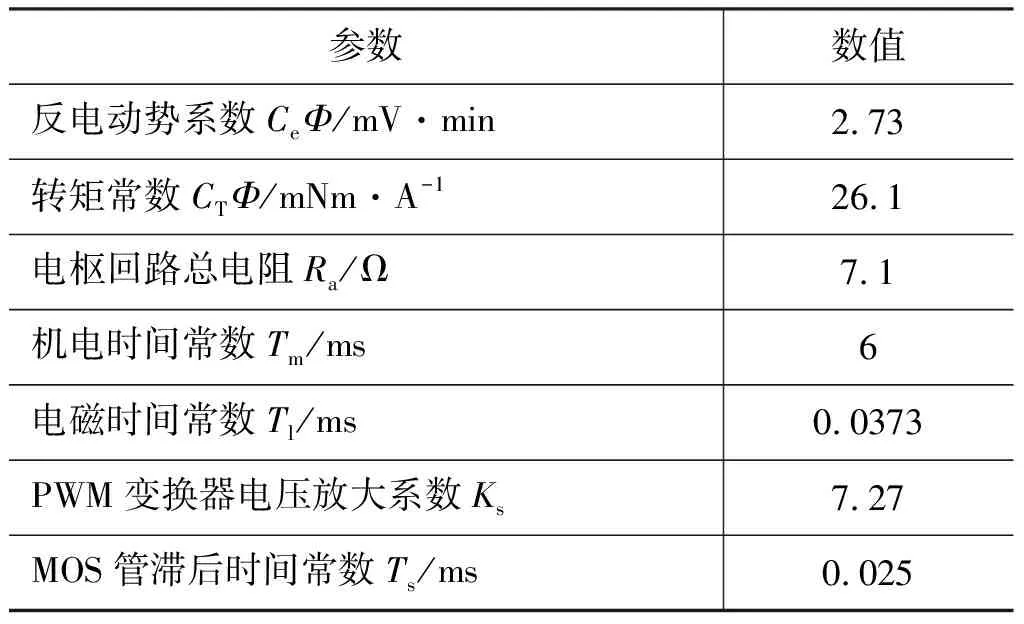
表1 直流有刷电机参数Tab.1 Parameters of DC brush motor

代入参数可得传递函数:

(4)

(5)

由于该算法要运用到实际单片机系统中,在MATLAB中采用零阶保持器法对系统模型(PWM变换器环节串联电机环节)进行Z变换离散化,采样时间5 ms,最终得到系统差分方程:

y(k)=0.432y(k-1)+1498.9u(k-1)+

12.17u(k-2)

(6)

式中,y(k) —— 速度输出值

u(k) —— 控制电压输入值

在实际系统中,单片机产生的控制电压为幅值3.3 V,频率为40 kHz,占空比可调的PWM波形,u(k)为控制电压均值,为0～3.3 V。

2 BP神经网络-无模型自适应控制器设计

螺杆点胶阀通常要适用不同黏度的介质,如UV胶、环氧胶、焊锡膏和导热硅脂等,其负载转矩有较大差别。在输送带有研磨颗粒的介质时,易对电机转速造成扰动。传统的PID控制算法,抗外部干扰和负载扰动能力不强,且不能保证一套参数在不同工况下对速度的控制保持很高精度,而人工调参需有很好的经验且费时费力,为生产上带来不便,需研究具有更好鲁棒性的控制算法。

无模型自适应控制作为一种针对非线性系统的数据驱动算法,选取无模型自适应控制器代替PID作为主控制器。在此基础上,针对其参数选取问题,采用BP神经网络在线优化无模型自适应控制器参数,实现其参数的自适应调整和系统的稳定控制。通过控制PWM占空比来改变加在电机两端平均电压,调节电机转速,进而控制螺杆点胶阀的出胶速度。出胶速度精度的提高,可以提升整个系统点胶效率,同时胶粒均匀圆润,点胶质量更好。整个控制系统结构图为:

如图2所示, 给定值与实际反馈值的误差送入MFAC控制器,控制器的三个参数由BP神经网络进行在线自适应调整,控制器输出作为系统输入经PWM变换器放大后对直流有刷电机进行转速控制。

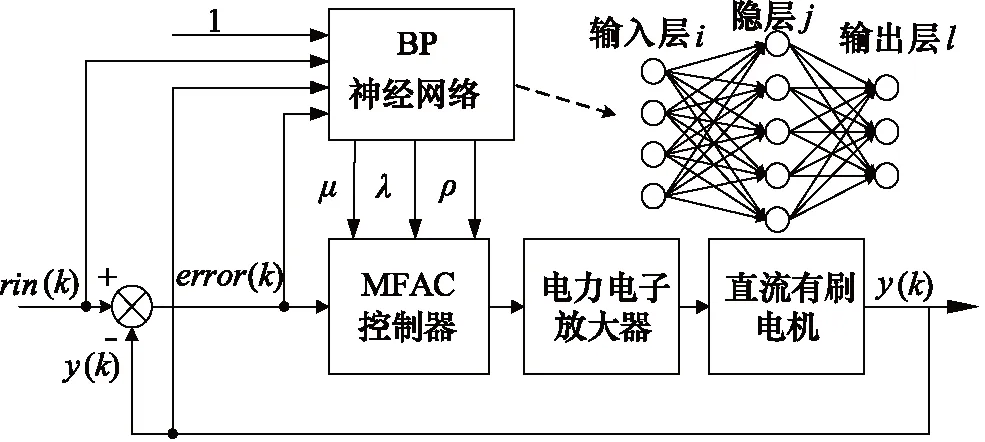
图2 BP神经网络-无模型自适应系统控制结构图Fig.2 Control structural diagram of BP neural network-model free adaptive system

2.1 无模型自适应控制

无模型自适应控制本质思想是在每一个动态工作点处建立一个对应的等价线性化模型,随着工作点的变化,等价线性模型也不断更新。其有三种形式分别为紧格式、偏格式和全格式,选用计算量小的紧格式无模型自适应控制方法,简述其推导过程[21]。

假定单输入单输出离散时间非线性系统:

y(k+1)=f(y(k),…,y(k-ny),u(k),…,

u(k-nu))

(7)

其中,y(k)∈R,u(k)∈R分别表示系统在k时刻的输出和输入;ny,nu是两个未知的正整数;f(…):Rnu+ny+2|→R为未知的非线性函数。如果该系统满足广义Lipschitz条件,即对任意k1≠k2,k1,k2≥0和u(k1)≠u(k2)有:

|y(k1+1)-y(k2+1)|≤b|u(k1)-u(k2)|

(8)

其中,b>0是一个常数。此时一定存在一个时变参数,使得其紧格式模型等价动态线性化为:

y(k+1)=y(k)+φ(k)Δu(k)

(9)

其中,Δu(k)=u(k)-u(k-1),φ(k)∈R为系统的伪偏导数PDD。

控制输入准则函数选取如下:

J(u(k))=|y*(k+1)-y(k+1)|2+

λ|u(k)-u(k-1)|2

(10)

其中,λ>0是一个权重因子,用来限制控制输入量的变化,y*(k+1)为期望的输出信号。

将式(9)代入准则函数,对u(k)求导,得到如下控制算法:

(11)

伪偏导数PDD估计准则函数为:

J(φ(k))=|y(k)-y(k-1)-φ(k)Δu(k-1)|2+

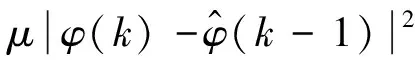
(12)

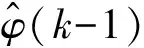
对式(12)关于φ(k)求极值,可得PDD估计算法为:

(13)

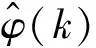
为使PDD估计算法对时变参数具有更强的跟踪能力,算法重置公式为:

(14)

综上所述,式(11)、式(13)、式(14)构成紧格式无模型自适应控制算法。

2.2 BP神经网络-无模型自适应控制算法

无模型自适应控制算法的参数对控制性能影响较大,同时较难通过人工调出最优参数,而BP神经网络具有一定自我调整和学习的能力,已广泛用于对控制器参数的调整。该算法原理为:输入正向传播和误差反向传播,采用梯度下降法,以误差最小为目标,不断修正权值系数,得到最优参数。采用BP神经网络对无模型自适应控制算法的三个参数μ、λ、ρ进行优化,利用BP神经网络的在线学习能力,实现参数的自适应调整。其实现的主要步骤为:

Step1选定BP神经网络的网络结构为4个输入节点,5个隐层节点和3个输出节点,给定初始化权值系数、学习速率β和惯性系数α。

为了保证收敛速度,网络结构不宜复杂。该网络设为4个输入节点,分别为rin(k)、y(k)、error(k)和1。3个输出节点,分别为无模型自适应控制的三个参数μ、λ、ρ。

Step2采样得到rin(k)、y(k)和error(k),并将其归一化处理后同1一起送入BP神经网络作为输入矩阵Oi(k)参与计算。

Step3 BP神经网络前向计算:神经网络输入矩阵乘以输入层到隐层的权值矩阵Wij(k)得到隐层节点的输入netj(k),输入层到隐层的激活函数采取正负对称的双曲正切函数,即:

(15)

代入netj(k),得到隐层节点的输出Oj(k),矩阵Oj(k)乘以隐层到输出层的权值矩阵Wjl(k),得到输出层节点的输入netl(k)。由于3个输出节点为无模型自适应的3个参数,均为非负数,所以隐层到输出层的激活函数取非负的Sigmoid函数,即:

(16)

代入netl(k),得到输出层输出Ol(k)即无模型自适应的三个参数。

Step4 BP神经网络的输出参数送入无模型自适应控制器得到控制器输出u(k),u(k)作为系统输入得到系统输出y(k)。

Step5 BP神经网络误差反向传播更新权值。取性能指标函数为:

E=1/2[rin(k)-y(k)]2

(17)

采用梯度下降法,按照对权值偏导的负梯度方向搜索,不断修正两个权值矩阵。因此隐层到输出层的权值增量公式为:

(18)

而其中:

(19)

而控制量对其三个参数的偏导为:

error(k)/[λ(k)+|φ(k)|2]2·

(20)

其中上式矩阵分别对应控制量u(k)对无模型自适应控制器三个参数ρ、λ、μ的偏导。而u(k)对参数ρ(k)的偏导不易求得,用符号函数来近似。

输出y(k)对控制量u(k)的偏导用符号函数近似为:

(21)

综上式,可得BP神经网络误差反向传播梯度公式,隐层到输出层权值的梯度公式为:

g′[netl(k)]·Oj(k)

(22)

其中令:

(23)

同理可得输入层到隐层权值的梯度公式为:

(24)

权值修正公式为:

W(k)=W(k-1)+ΔW(k)

(25)

当前时刻权值为上一时刻权值加当前时刻权值增量。

Step6 置k=k+1,目标函数达到极小值时结束,否则返回到Step2。经过不断在线学习,实现无模型自适应参数的自适应调整。

BP神经网络原理简单,易于实现,在系统运行过程中,将该时刻采样到的数据送入网络,正向输出MFAC参数,并反向调整权值,下一时刻如此循环,直到使系统误差最小,即达到稳定状态,实现参数的在线调整。

3 仿真与实验验证

为验证BP神经网络-无模型自适应控制算法的有效性,分别采用MATLAB和搭建的实验平台对电机系统的速度控制进行仿真与实验验证,并用传统PID控制算法与BP神经网络-无模型自适应控制算法进行对比,仿真和实验时间为0.3 s和0.5 s,系统的给定转速为中低速1000 r/min。其工况为:空载并在0.15 s和0.25 s时刻突加负载扰动,扰动设定为在其开环状态下稳定为900 r/min。主要评价指标有调节时间、超调量、稳态误差等,其中调节时间的误差带选取为±2%。

3.1 仿真验证

编写BP-MFAC算法代码,对系统速度控制进行仿真,伪偏导数PDD的初值为φ(1)=1,步长η取固定值1,系统稳定时自适应参数为:μ=0.2259,λ=0.8427,ρ=0.7426;采用PID选取一组较好的参数为:Kp=0.00005,Ki=0.00015,Kd=0.0001。扰动添加方式为:u(k)值为0.3757时,电机速度稳定在1000 r/min。在0.15 s时刻将控制电压u(k)均赋值为0.31,使电机速度降为900 r/min,两种算法控制效果如图3所示。

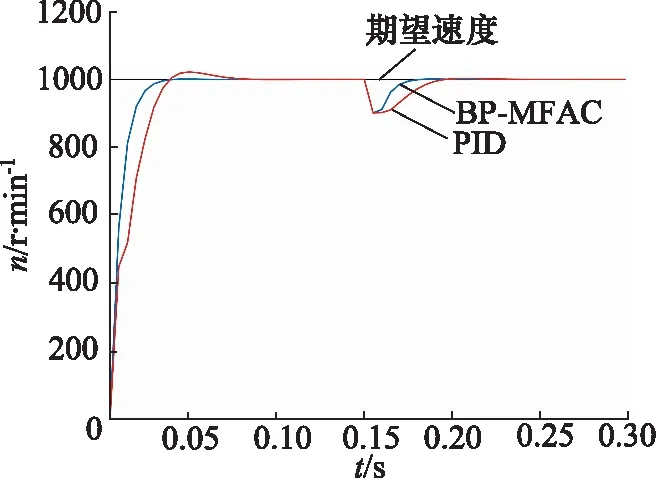
图3 BP-MFAC和PID仿真结果Fig.3 BP-MFAC and PID simulate results

如图3所示,n为电机转速,t为时间。BP-MFAC算法相比于传统PID算法,超调量更小,调节时间更短,在出现突加负载扰动的情况下,能更快地达到期望速度,表现出更好的抗负载扰动能力。

3.2 实验验证

为进一步验证仿真实验的有效性,用螺杆点胶阀系统进行实验验证。电机驱动器设计选用STM32F103CBT6作为主控芯片,主频为72 MHz,采用测频法测速,为兼顾测频精度、控制实时性、计算量,控制周期选取为5 ms。给定速度与编码器反馈的速度作差,将误差送入控制器得到控制电压,经PWM变换器放大,驱动电机,形成整个系统的闭环控制。其中PID参数选取为:Kp为0.22,Ki为0.4,Kd为0.1,经优化的MFAC参数为:μ为6.8664,λ为1.6645,ρ为0.4131。扰动添加方式为:电机在开环状态将占空比设为12%(忽略死区时间),此时转速大致稳定在891～914 r/min,在0.25 s将占空比均赋值为12%。采用串口通信打印出电机实时速度,将数据进行均值滤波,去除部分噪声,得到实验结果图如图4所示。

图4 BP-MFAC和PID实验结果Fig.4 BP-MFAC and PID experimental results

如4图所示,n为转速,t为时间。相比于PID控制,BP-MFAC算法超调量较小,稳态误差更小,调节时间更短;在突加负载扰动时,动态降落更低,而且能更快回到期望速度,抗负载扰动性能更好。

综上,仿真和实验的具体指标如表2所示。

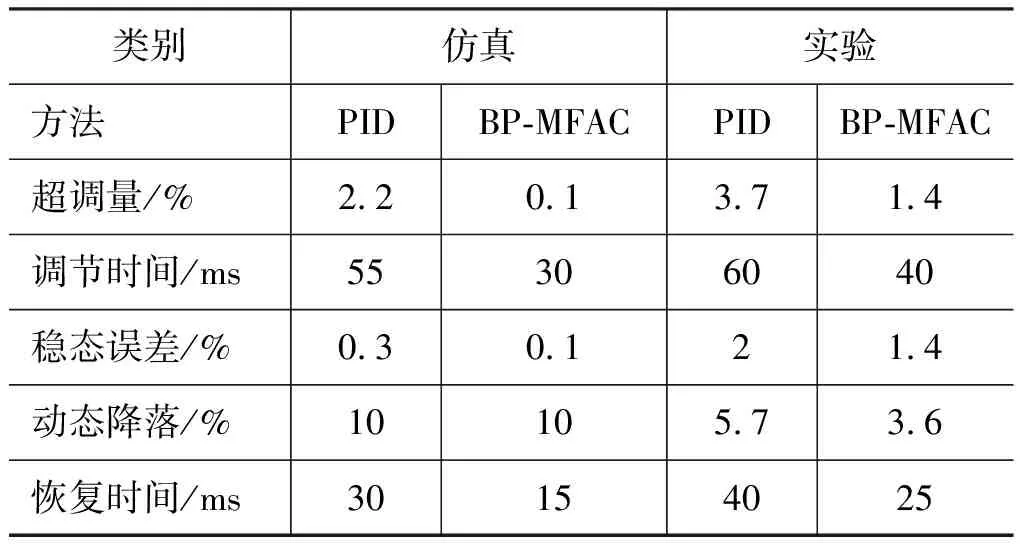
表2 仿真及实验结果Tab.2 Simulate and experimental results

4 结论

针对螺杆点胶阀对速度控制的高精度,以及较高抗负载扰动能力的要求, 采用BP神经网络-无模型自适应的控制方法对电机系统进行仿真和实验,通过BP神经网络在线调整无模型自适应控制器的三个参数,无需再进行复杂的人工参数整定。相比于传统增量式PID控制,该算法具有更短的调节时间,更小的超调量、稳态误差和更高的抗负载扰动能力。