基于机器学习的离港航空器滑出时间预测

陈宽明, 王楚皓, 夏正洪

(中国民用航空飞行学院空中交通管理学院, 广汉 618307)

一次完整的飞行过程由起飞前滑行、起飞、爬升、巡航、下降、进近着陆、降落后滑行7个阶段组成,航空器在机场场面的运行过程往往被认为是影响飞行效率的关键环节。随着民航交通流量的持续快速增长,大型机场的跑滑系统越来越复杂,航班地面滑行的时间已经超过25 min,严重制约着机场场面运行效率的提升,并伴随有滑行冲突、延误等问题。航空器滑出时间是指航班的实际起飞时刻与推出开车时刻的时间间隔,它是衡量大型繁忙机场场面运行效率的重要指标。因此,科学准确地预测航空器滑出时间,对于提升机场场面运行效率有重要意义。

外国关于滑出时间预测的研究始于21世纪初,基于起飞队列长度、跑道、机型等因素构建了滑出时间的多元线性回归预测模型,±5 min范围内的预测精度不足70%。现有研究成果主要包括基于仿真模拟和数学建模。仿真模拟通常需要考虑机场的跑道、滑行道构型和滑行冲突种类及解脱方法,同时对进/离港航空器的场面运行过程进行仿真,从而得到离港航空器的滑出时间预测结果。其中比较典型的是Lee等[1]建立的滑出时间快速仿真预测模型,±5 min范围内的预测精度约为75%。历史数据往往可以揭示大型机场场面的滑行规律,反映出滑出时间与其影响因素之间的相关性。因此,基于数学建模的方法[2]主要有线性回归、BP(back propagation)神经网络、支持向量机、深度学习等,并且通过训练集、验证集和测试集的划分来验证数学方法对于滑出时间预测的准确率。George等[3]基于航班历史数据对航空器的滑出时间进行了动态预测,提出了基于强化学习的Q-Learning方法。Gu等[4]提出了基于梯度提升回归树(gradient boosting regression tree,GBRT)预测滑行时间。 Yin等[5]从宏观网络角度预测航空器滑出时间。

中国滑出时间预测相关研究起步较晚。2016年,冯霞等[6]首次基于排队论构建了中国单跑道机场的滑出时间预测模型,±5 min内的准确率仅为79%。现有研究成果主要分成两个方向:一是采用不同的算法来对滑出时间进行预测,主要包括支持向量机(support vector machine,SVM)[7]、贝叶斯网络[8]、深度学习[9]、BP神经网络[10]等,旨在提升预测精度。Li等[11]运用多种深度学习的算法来预测航空器滑出时间,±5 min内的准确率可达到90%。二是基于滑出时间的预测结果来对航空器的推出策略进行优化,从而减少推出等待过程中的燃油消耗和污染排放。Lian等[12]提出了基于滑出时间预测的动态推出控制策略。

综上所述,现有研究成果以单跑道机场为研究对象,分析了可量化的因素对滑出时间的影响。由于缺乏对机场场面运行态势的深入分析,从而导致影响因素的量化发生偏差,预测结果存在较大差异,并且缺乏讨论多跑道机场的起飞使用跑道对滑出时间的影响。鉴于此,分析进/离港航空器场面滑行的时空分布特征,准确定义同时段滑行的进/离港航空器数量、起飞队列长度、30 min平均滑出时间,并将使用跑道进行数值映射(量化),采用3种机器学习方法对滑出时间进行预测,以期获得更准确的滑出时间预测结果,为航空器的推出控制策略提供数据参考。

1 滑出时间影响因素及相关性分析

1.1 机场场面运行态势分析

机场场面交通流是影响大型枢纽机场航空器滑出时间的主要因素。离港航空器在机场场面的滑行过程中,常与其他航空器一起争夺跑道、滑行道资源,有时甚至会因为等待而造成滑出时间的增加,即航空器的滑入滑出过程在时空上是相互耦合、相互依存,会形成较为复杂的机场场面运行态势,如图1、图2所示。

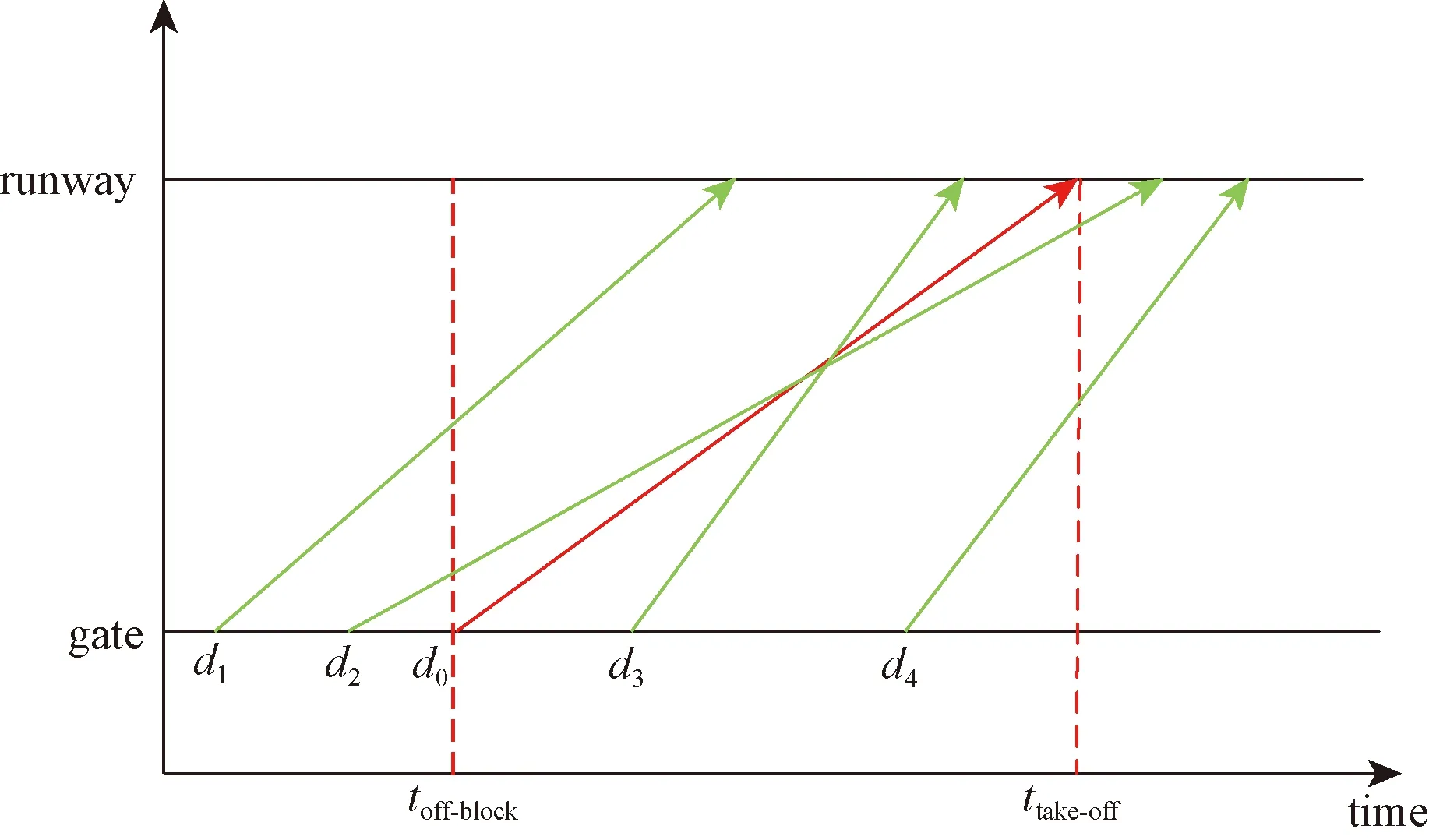
runway为跑道;gate为停机位;time为时间;toff-block为推出时间;ttake-off为起飞时间图1 离港航空器之间的时空关系Fig.1 Space-time relationship between departure flights

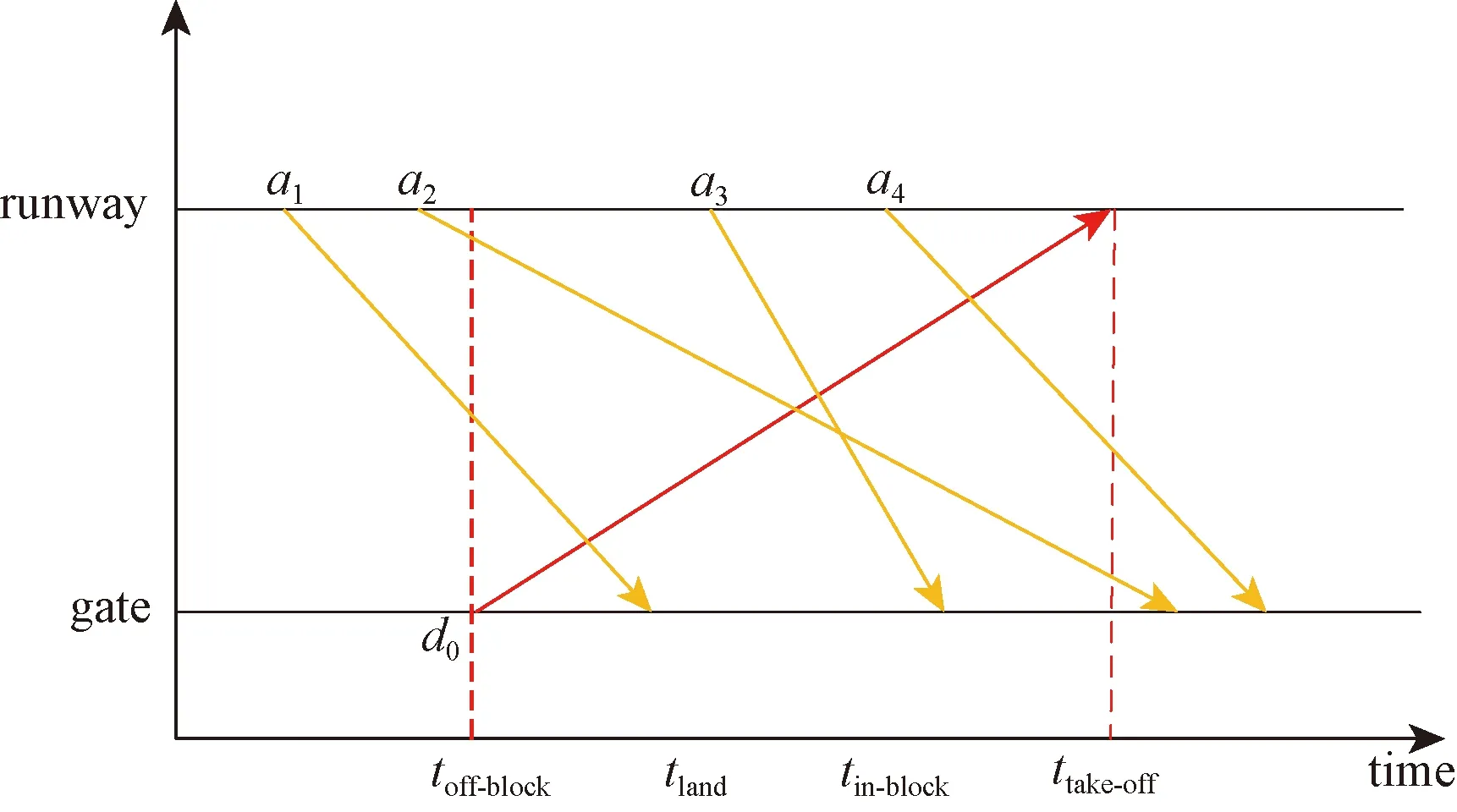
toff-block为推出时间;tland为落地时间;tin-block为滑入时间;ttake-off为起飞时间图2 进港航空器与离港航空器的时空关系Fig.2 Space-time relationship between inbound flights and outbound flights

图1中,d0为待研究的离港航空器i,其推出开车时间(actual off-block time,AOBT)和起飞时间(actual take-off time,ATOT)分别为AOBTi和ATOTi。d1、d2、d3、d4分别为与d0有时空交集的4种离港航空器,即任意一种离港航空器都可影响d0的滑出时间。

d1为航空器j“推出早、起飞早”,其推出开车时间和起飞时间分别为AOBTj和ATOTj,与航空器i的推出开车时间和起飞时间的关系可表示为

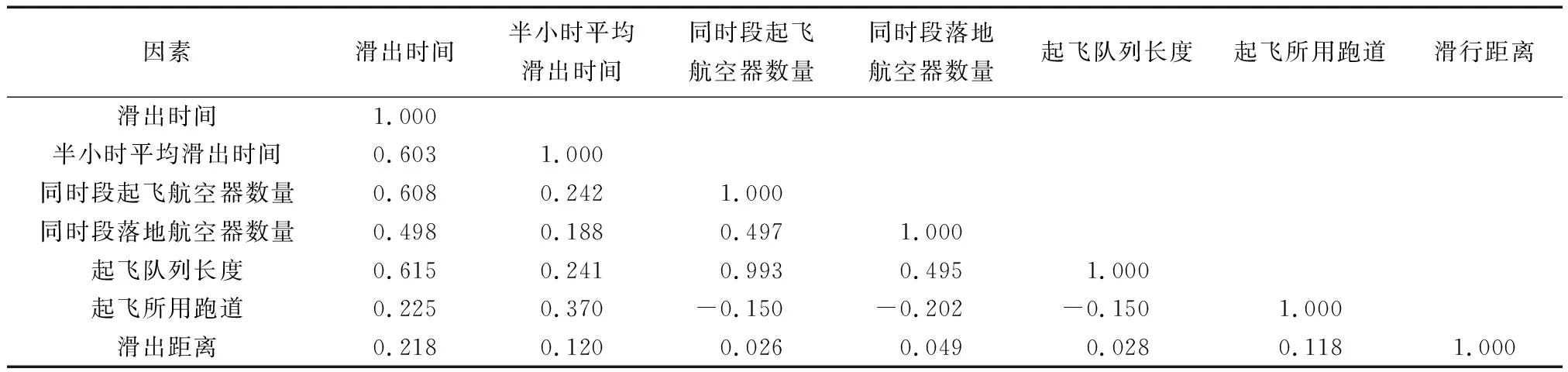
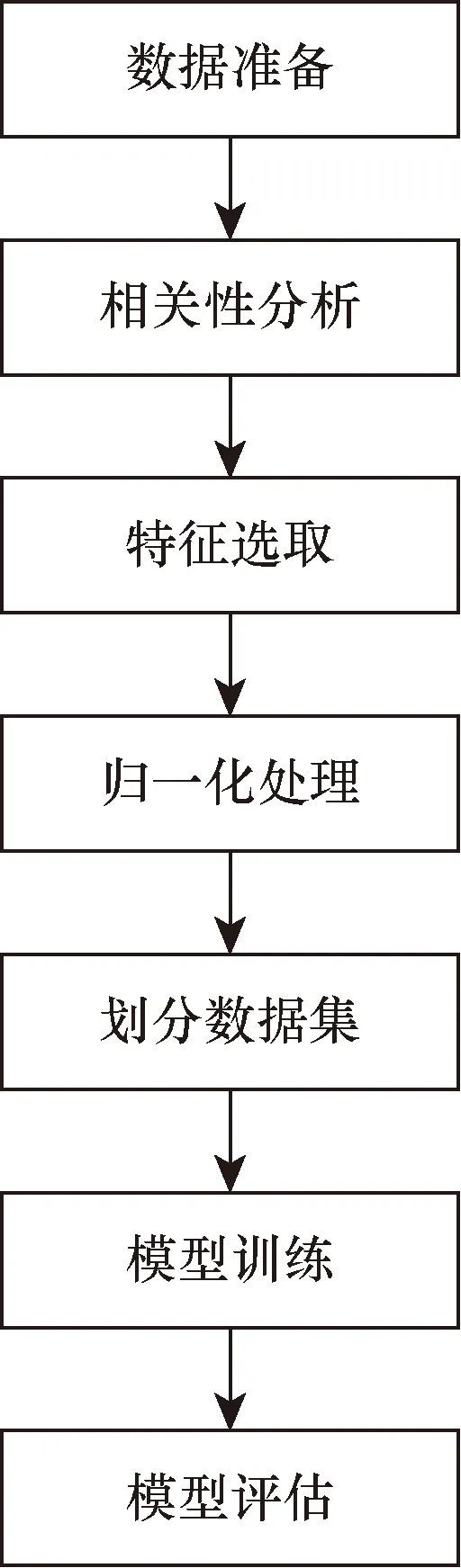
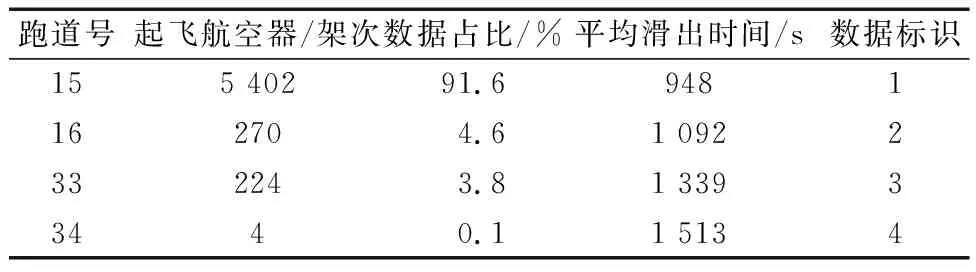
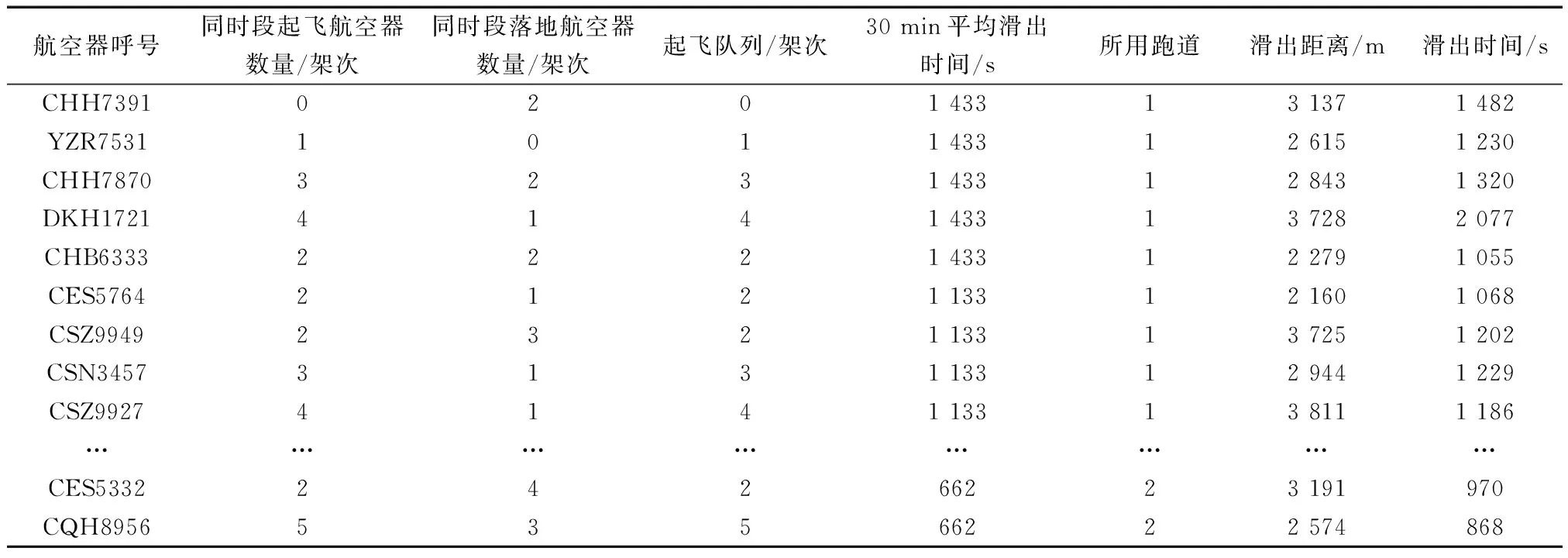
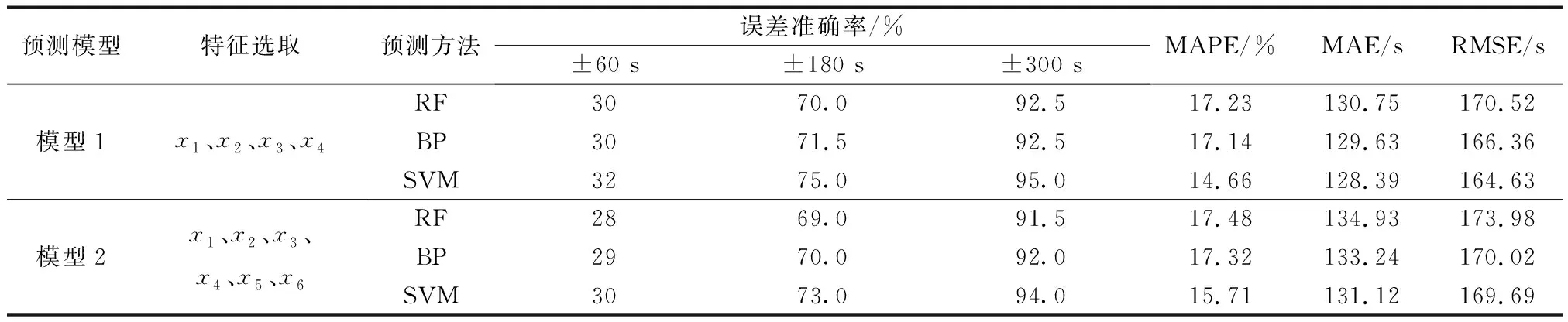
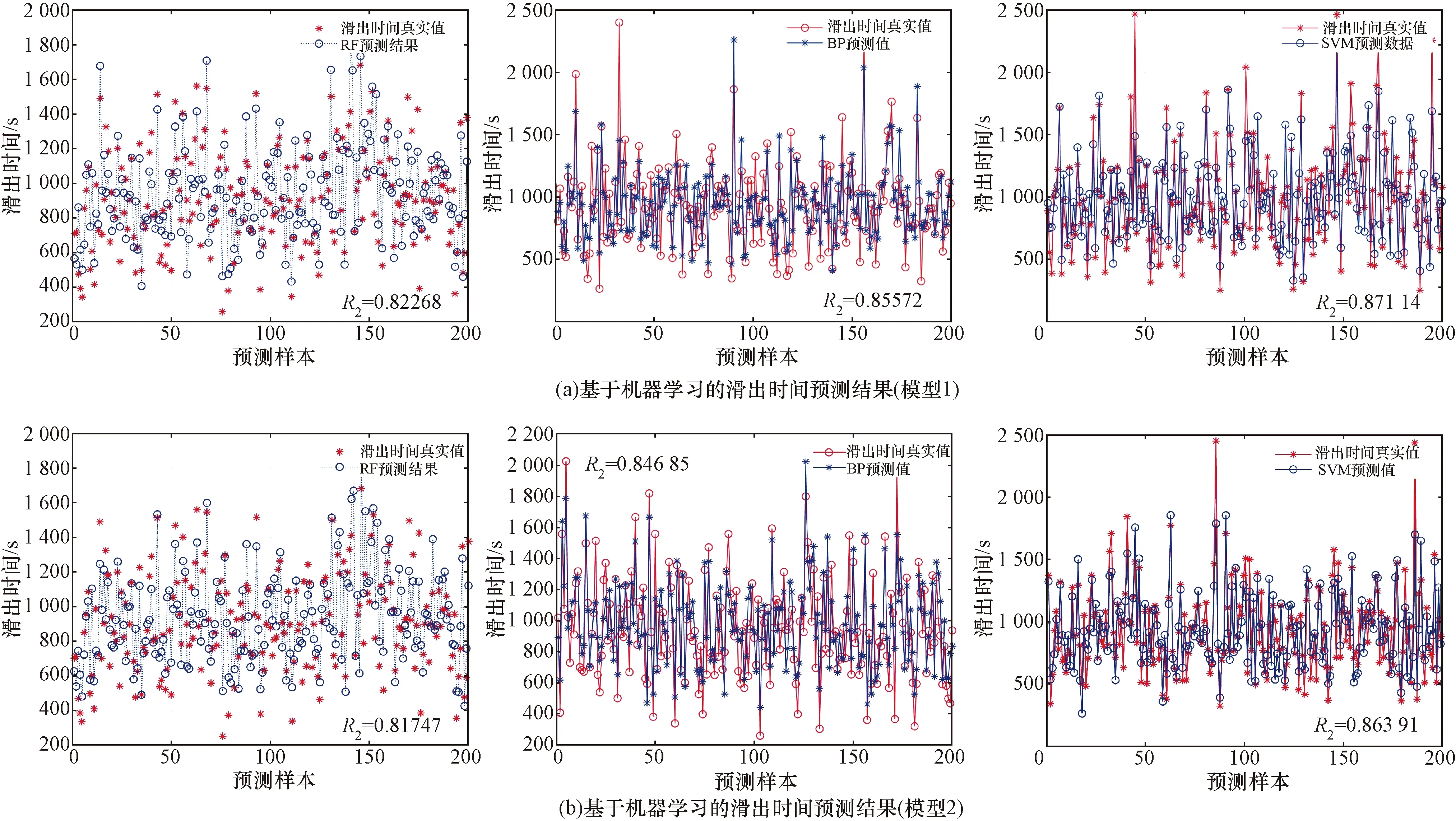
d1,{AOBTj

(1)

d2为航空器j“推出早、起飞晚”,与航空器i的推出开车时间和起飞时间的关系可表示为

d2,{AOBTjAOBTi}

(2)

d3为航空器j“推出晚、起飞早”,与航空器i的推出开车时间和起飞时间的关系可表示为

d3,{ATOTjAOBTi}

(3)

d4为航空器j“推出晚、起飞晚”,与航空器i的推出开车时间和起飞时间的关系可表示为

d4,{AOBTjAOBTi}

(4)

图2中,d0为待研究的离港航空器i,a1、a2、a3、a4分别为与d0有时空交集的4种进港航空器,即任意一种进港航空器都可影响d0的滑出时间。

a1为航空器j“落地早、进位早”,其落地时间(actual landing time,ALDT)和滑入时间(actual in-off block time,AIBT)分别为ALDTj和AIBTj,与航空器i的推出开车时间和起飞时间的关系可表示为

a1,{ALDTjAIBTj>

AOBTi}

(5)

a2为航空器j“落地早、进位晚”,与航空器i的推出开车时间和起飞时间的关系可表示为

a2,{ALDTjATOTi}

(6)

a3为航空器j“落地晚、进位早”,与航空器i的推出开车时间和起飞时间的关系可表示为

a3,{AOBTi

AIBTj

(7)

a4为航空器j“落地晚、进位晚”,与航空器i的推出开车时间和起飞时间的关系可表示为

a4,{AOBTi

ATOTi}

(8)

1.2 滑出时间影响因素

通过文献追踪可知,现有研究的某些滑出时间影响因素参量表达不太准确,导致预测结果的精度不高。因此,基于机场场面运行态势分析进/离港航空器滑行的时空分布特征,力求将这些可量化的影响因素描述的更为准确。同时,滑出时间还受到流量控制、恶劣天气、起飞使用跑道、机型等不可量化因素的影响。

(1)x1为同时段滑行的离港航空器数量,即与待研究对象d0有时空交集关系的所有离港航空器,单位:架次,可表示为

x1=d1+d2+d3+d4

(9)

(2)x2为同时段滑行的进港航空器数量,即与待研究对象d0有时空交集关系的所有进港航空器,单位:架次,可表示为

x2=a1+a2+a3+a4

(10)

(3)x3为起飞列队长度,即与待研究对象d0有时空交集关系且起飞时间更早的所有离港航空器,单位:架次,其表达式如式(11)所示。起飞队列越长,则航空器从跑到外等待至起飞所需的时间就会越长。

x3=d1+d3

(11)

(4)x4为30 min平均滑出时间,单位:s,其表达式如式(12)所示。场面滑行的航班越多,则单个离港航空器的滑出时间和30 min平均滑出时间就会越长。

(12)

式(12)中:ti为第i架离港航空器的滑出时间;n为30 min中滑出的离港航空器数量。

(5)x5为离港航空器滑行距离,单位:m,其表达式为

(13)

式(13)中:da,i为航班i滑行路径的测量长度;db为跑道的测量长度;3 600为以米为单位的跑道长度。

(6)x6为离港航空器起飞使用的跑道。起飞跑道的选择与该机场的地面运行模式直接相关,对于同一停机位的离港航空器使用不同的起飞跑道,滑行路线以及滑行距离是不同的,滑行所需时间也会不同。但是,由于跑道号不能直接运用于滑出时间预测,可根据其使用跑道的4个方向,使用1～4将其进行量化。

1.3 相关性分析

所用数据来源于中南某枢纽机场2018年8月6日—8月19日共计2周的实际运行数据,数据集共有记录12 103条,包含离港航班6 032架次和进港航班6 071架次;每条记录由飞机呼号、机型、实际起飞时间、实际撤轮档时间、实际落地时间、跑道号、停机位等关键信息组成。通过对数据整理,删除重复及异常数据,并根据式(9)～式(13)依次得到同时段滑行的离港航空器数量,同时段滑行的进港航空器数量,起飞队列长度,30 min平均滑出时间,滑行距离,起飞所用跑道以及实际滑出时间,并使用Minitab软件对其进行相关性分析,如表1所示。

表1 滑出时间影响因素相关性分析结果Table 1 Correlation analysis results of influencing factors of taxi-out time

根据相关性系数可知,滑出时间影响因素相关性排序为:起飞队列长度、同时段起飞航空器数量、半小时平均滑出时间、同时段落地航空器数量、起飞所用跑道、滑出距离。其中,显著相关的有起飞队列长度、同时段起飞航空器数量和半小时平均滑出时间(相关系数≥0.6);中度相关的有同时段落地航空器数量(0.6>相关系数≥0.3);弱相关的有使用跑道和滑出距离(相关系数<0.3)。

2 基于机器学习的离港航空器滑出时间预测

2.1 机器学习算法及步骤

机器学习是一门多领域交叉学科,算法可基于大型数据集进行训练获得模型和相关性,根据数据分析结果做出最佳决策和预测。常用的机器学习算法有逻辑回归(logistic regression, LR)、朴素贝叶斯(naive bayes, NB)、K近邻法(K-nearest neighbors, KNN)、决策树(decision tree, DT)、随机森林、支持向量机、人工神经网络(artificial neural network, ANN)等。选用RF、SVM、BP神经网络对离港航空器的滑出时间进行预测,算法流程如图3所示。

图3 基于机器学习的滑出时间预测流程Fig.3 Taxi-out time prediction process based on machine learning

Step 1数据准备。原始数据的数量和质量直接决定预测模型输出结果的好坏。将收集的原始数据进行去重复、错误修正以及标准化处理。

Step 2相关性分析。对收集的数据进行分析,找出每列数据的最大值、最小值、平均值、方差、中位数等信息;同时确定自变量和因变量,并计算相关系数。

Step 3特征选取。特征的好坏基本上决定了分类器的效果,基于相关性分析结果对自变量进行筛选,选择更合适的特征。

Step 4归一化处理。对特征提取结果进行再加工,增强特征表示能力,防止模型过于复杂和学习困难。

Step 5划分数据集。通常需要将数据划分为训练集和测试集,训练集数据用来训练模型,测试集用于模型的评估。

Step 6模型训练。选定合适的算法如随机森林、支持向量机、BP神经网络作为分类器,使用训练集数据对其进行训练,以最小误差作为目标函数得到稳定的分类器。

Step 7模型评估。将测试集数据导入到训练好的分类器中得到预测值,再与真实数据进行对比,从而判定模型的好坏。

2.2 模型构建

通过对样本数据进行分析,15号跑道起飞的航班架次占比高达91.6%,且平均滑出时间仅为948 s,为该机场的主起跑道。16号跑道起飞的航班架次为4.6%,在离港高峰时可以使用该跑道进行独立平行离场,平均滑出时间1 092 s,如表2所示。当风向发生改变时(东南风的顺风分量超过5 m/s),可使用33号跑道起飞,平均滑出时间为1 339 s; 34号跑道几乎不用于起飞。可见,离港航班使用不同的跑道起飞,平均滑出时间差异较大。因此,本文将起飞跑道作为滑出时间的一个影响因素,15号跑道对应的数据标识为1,以此类推。

表2 不同跑道的滑出时间分析Table 2 Analysis of taxi-out time of different runways

为讨论跑道使用对滑出时间的影响,基于相关性分析结论进行特征选取,构建了两种离港航空器滑出时间预测模型,如表3所示。

表3 滑出时间预测模型Table 3 Taxi-out time prediction model

2.3 模型评估

以平均绝对误差百分比(mean average percentage error,MAPE)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE),以及±1、±3、±5 min的误差来评价基于机器学习的离港航空器滑出时间预测精度,计算公式分别为

(14)

(15)

(16)

式中:n为待预测的离港航空器数量;pi为离港航空器i的可变滑出时间预测值;oi为离港航空器i滑出时间的真实值。

3 滑出时间预测典型实例

3.1 数据准备

研究对象为中国中南某枢纽机场,该机场东跑道3 400×45 m,西跑道3 800×60 m,东西跑道之间间距约为1 590 m,离港航空器可以选择从15、16、33、34号跑道起飞。通过对该机场2018年8月2周的数据进行整理,删除重复及异常数据,最终得到样本数据5 900条,如表4所示。

表4 整理后的样本数据集Table 4 Sorted sample data set

3.2 预测结果

将所有样本数据导入MATLAB中并随机打乱顺序,选择前5 700个数据为训练集,后200个数据作为测试集,并将其进行归一化处理。设置随机森林中决策树的数量为100,树的特征个数为34,最大深度为10。设置支持向量机的惩罚系数C为3,Gamma为1.5。设置BP神经网络最大迭代次数1 000次,学习率为0.01,目标收敛误差为0.001。用训练集数据训练3种算法的分类器,然后将测试集数据代入训练好的分类器中进行预测,并将结果进行反归一化,得到预测结果和评估结果,如表5、图4所示。

表5 滑出时间预测结果误差分布对比Table 5 Comparison of error distribution of taxi-out time prediction results

图4 滑出时间预测结果Fig.4 Taxi-out time prediction results

从表5、图4所示的预测值对真实值的拟合程度来看,3种算法均能完成对离港航班滑出时间的有效预测,且SVM分类器的预测结果效果最好,其次是BP神经网络和RF。模型1的曲线拟合优化程度R2均大于模型2,采用SVM分类器时拟合优度分别为0.871 1、0.863 9,证明了不相关的因素引入模型后会导致预测结果的拟合程度降低。

根据模型评估标准,3种机器学习均可有效地预测离港航空器的滑出时间,其分类器的优劣排序为SVM、BP神经网络、RF。模型1的预测效果整体优于模型2,说明引入弱相关性的特征(使用跑道、滑行距离)后,模型的预测准确率会有一定程度的降低;同时,预测结果的平均绝对百分比误差、平均绝对误差、均方根误差均有增加。根据现有民航航班延误定义标准,航班实际撤轮挡时间超过计划时间15 min的情况为航班出港延误。为保障航班的正常运行,在合理的时间余度内选择±60、±180、±300 s进行测评。基于SVM分类器的离港航空器滑出时间预测效果最佳(模型1),误差在±60、±180、±300 s的准确率分别为32%、75%、95%,MAPE、MAE、RMSE分别为14.66%,128.39 s,164.63 s。

4 结论

(1)分析了进/离港航空器在机场场面运行的时空分布特征,准确定义并量化了滑出时间影响因素。

(2)对滑出时间影响因素进行了相关性分析,显著相关的有起飞队列长度、同时段起飞航空器数量和半小时平均滑出时间;中度相关的有同时段落地航空器数量;弱相关的有使用跑道和滑出距离。

(3)构建了基于机器学习的航空器滑出时间预测模型,通过对比分析可知,SVM分类器对本文数据的适应度最佳,其次是BP神经网络和RF。

(4)下一步的研究工作将讨论恶劣天气对滑出时间的影响。