各向异性孔隙地层随钻声波测井理论模拟及应用
郭同政, 申富豪, 饶博, 苏远大*
(1.中石化经纬有限公司, 青岛 266000; 2.中海石油(中国)有限公司海南分公司, 海口 570311; 3.中国石油大学(华东)深层油气重点实验室, 青岛 266580)
渗透率是衡量储层产出能力的重要参数之一,准确地求取储层的渗透率一直以来是测井解释的一项重要研究课题。目前基于声波测井资料的渗透率反演方法大多是在假设地层为均匀各向同性介质的前提下建立的。然而地下岩石大多为层状沉积,具有明显的横观各向同性特征(transverse isotropy, TI)。为了能够更加准确地描述地下油气储层的弹性力学和渗流性质,有必要对综合考虑沉积岩孔渗性质和各向异性的横观各向同性孔隙介质模型井孔声场问题进行详细研究。
在钻后电缆声波测井中,Biot[1]在考虑固体介质与孔隙流体间黏滞耦合的基础上,将孔隙介质的渗透率、孔隙度及孔隙流体性质引入波动方程,建立了孔隙介质弹性波理论。Rosenbaum[2]首先将Biot理论与井孔声学相结合研究了孔隙介质井孔声波的传播问题。Schmitt[3]进一步研究了径向分层孔隙地层电缆单极声波测井问题。针对各向异性和渗透性共存的复杂储层,Zhang[4]分析了井内多极声场中临界折射波的激发谱。特别地,当井轴与地层对称轴重合时,可以用VTI(vertical transverse isotropy)模型来求解地层各向异性特征。陈雪莲等[5]研究了径向分层VTI孔隙模型中斯通利波和弯曲波传播特性受侵入带的影响程度。相较于电缆测井,随钻声波测井(acoustic logging while drilling,ALWD)实时性更高。围绕随钻声波测井技术,中外学者在方法理论、仪器研发及工程应用等方面开展了许多卓有成效的研究工作[6-12]。针对孔隙地层及VTI地层等复杂地层条件下的随钻声波测井数值模拟及应用也得到长足的发展。Tang等[13]通过现场资料处理分析,验证了利用随钻斯通利波进行地层渗透率测量的可能性。李希强等[14]对VTI地层中随钻多极子模式波的频散、激发强度以及灵敏度特征进行了研究。唐晓明[15]、Tang等[16]和许松等[17]将孔裂隙统一理论引入随钻声波测井领域,并尝试利用随钻声波资料在孔裂隙地层中识别气层。王瑞甲等[18]针对VTI地层随钻四极子波进行了数值模拟,并对其在径向上的探测范围进行了研究。卫建清等[19]运用有限差分的方法研究了井轴与地层界面斜交情况下随钻四极模式波的传播规律。庄春喜等[20]利用等效仪器理论快速模拟了随钻斯通利波的频散曲线并成功对地层渗透率进行了评价。Li等[21]综合利用随钻单极和四极声波资料反演了VTI地层各向异性。饶博等[22]给出了VTI地层井孔声场复数域解析函数的单值化定义,并以此对随钻多极子声场进行了分波分析。
前人已经对随钻声波测井进行了较为充分的研究,然而目前鲜见对于随钻声波测井在更为复杂的横观各向同性孔隙地层中数值模拟及应用的相关报道。鉴于此,建立随钻声波测井模型,以Biot理论为基础研究弹性波在横观各向同性孔隙地层中的传播机制,考察地层渗透率及弹性参数对随钻多极子模式波速度频散的影响,验证了利用随钻声波测井资料反演地层横波各向异性和水平向渗透率的可行性。
1 横观各向同性孔隙地层随钻声波测井理论
图1给出了横观各向同性孔隙地层充液井孔中的随钻声波测井模型的示意图,该模型包含两个部分:一是井孔内的径向分层介质,由流体-固体交错的径向分层介质组成;二是井外VTI孔隙地层,其对称轴与井轴重合。如图1(a)所示,声波发射换能器和接收器阵列均安装在钻铤外壁上,因此可以将声波发射换能器模拟为紧贴在钻铤外壁的环状多极子声源。如图1(b)所示,钻铤在井孔中完全居中,其内外均为钻井液所填充,井外为无限大横观各向同性孔隙地层。

ra、rb和R分别为钻铤内径、钻铤外径和井眼半径大小图1 横观各向同性孔隙地层随钻声波测井模型示意图Fig.1 Schematic diagrams of transverse isotropic porous model for ALWD
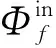
(1)
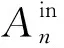
在钻铤内,同时考虑由内向外发散的出射波和由外向内汇聚的入射波,则钻铤内各位移势函数的解可表示为
(2)
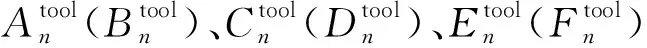

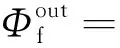
(3)

在无限大横观各向同性孔隙地层中,根据Biot理论,横观各向同性流体饱和的孔隙地层中应力和应变的本构关系由下式给出,TI双相孔隙介质中应力和应变关系可表示为
(4)
式(4)中:σrr、σθθ、σzz分别为骨架径向、环向和轴向正应力,σrz、σθz、σrθ分别为环向、径向和轴向截面的切应力;S为流体的应力;err、eθθ、ezz分别为固相介质径向、环向和轴向正应变,erz、eθz、erθ分别为环向、径向和轴向截面的切应变;ε为液相的应变;Cij(i,j=1,2,…,6)为应力-骨架应变关系的弹性系数;M、Q分别为固相和液相之间相互作用的弹性系数;R为液相部分的弹性系数。
假设时间因子为e-iωt可以得到弹性波满足的频域动力学方程为
(5)
式(5)中:U和V分别为骨架和孔隙流体的位移;γ11、γ12、γ21、γ22为与质量耦合系数、流体的黏度及渗透率相关的参数。
通过求解式(5)可获得4个体波解,即准快纵波、准慢纵波、准SV波和SH波,具体推导过程参考文献[3]。在此基础上,将井孔内、外各部分声场的应力和位移分别代入边界条件(在VTI孔隙地层和流体边界条件中,除了满足径向位移和正应力连续,切应力为零之外,还需要满足井内流体压力与地层孔隙内的流体压力连续),即可得到横观各向同性孔隙地层随钻声场的矩阵方程为
{Hij}13×13{Oj}13×1={bi}13×1
(6)
式(6)中:Hij为VTI孔隙地层随钻声场的特征矩阵[23];Oj为振幅系数向量;bi为声源向量。
随钻仪器外环上声压场的波形计算公式为
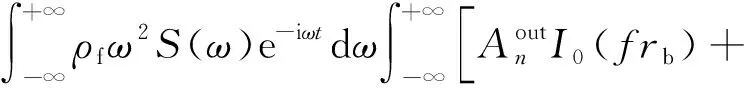
(7)
式(7)中:P为井轴接收信号(声压信号);t为时间;ρf为井内流体密度;rb为钻铤外径;I0和K0分别为第一类和第二类0阶变型贝塞尔函数;S(ω)为声源函数的频谱,其函数形式可以任意选取,采用中心频率为ω0的余弦包络脉冲[23]。
随钻声场中模式波的频散特征由频散方程系数矩阵Hij确定,令其行列式D为零,得到各模式波的频散方程为
D(k,ω)=detH(k,ω)=0
(8)
通过求解式(8)在不同频率下的根并结合式(9)可计算得到各模式波的相速度(vphase)和群速度(vgroup)频散曲线。
(9)
式(9)中:Re表示取变量的实部。
2 数值计算结果及分析
在推导得到横观各向同性孔隙地层随钻声波测井声场的波形计算公式[式(7)]及频散方程[式(8)]的基础上,通过求解频散方程分析了随钻多极子声场各阶模式波的频散特征,并采用实轴积分的方法[24]分别模拟计算了快速和慢速地层条件下的随钻多极子声波测井的全波波形。计算所用的模型参数分别如表1~表3所示。其中,表1为钻井液和钢制钻铤的声学参数,表2和表3分别为井外地层中固相和孔隙流体相的声学参数。

表1 钻井液及钻铤参数Table 1 Acoustic parameters of drilling fluid and collar
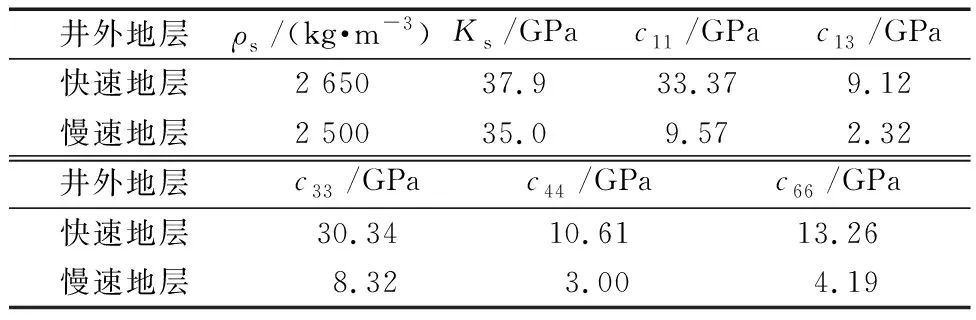
表2 井外地层固相参数Table 2 Solid phase parameters of a porous formation

表3 井外地层孔隙流体参数Table 3 Fluid parameters of a porous formation
2.1 单极子声场
图2给出了快速和慢速VTI孔隙地层中随钻单极声场的各阶模式波相速度频散曲线。从图2(a)可以看出,对于快速VTI孔隙地层,在声波测井常见的0~25 kHz频率范围内一共存在5种模式波。其中黑色标识符“ST”表示在井壁处固-液界面产生的斯通利波(Stoneley wave),该模式波的速度最慢,没有截止频率,在高频处趋于井内流体速度,且随着频率的降低,斯通利波的速度也逐渐减小。与弹性地层不同的是,由于地层孔隙流体与井内流体在井壁处可以自由交换,地层的渗透性使得斯通利波速度不再有低频极限且频散效应增强,这也是随钻斯通利波可以被用来反演地层渗透率的原因。图2中红色标识符“IN-ST”表示的是在钻铤内壁激发的内斯通利波(inner Stoneley wave),该模式波的速度略高于斯通利波速度,在全频域范围其相速度频散十分微弱,整体趋近于井内流体速度。“P-R”表示在井壁处激发的伪瑞利波(Pseudo-Rayleigh wave),其在截止频率处的波速约为地层横波速度。“C-1”表示的是一阶钻铤模式波,这是一种全频域频散的模式波,且在中间频段处频散较为严重。“C-2”表示二阶钻铤模式波,其相速度与钻铤纵波速度接近,也存在低频截止现象,只在高频段才能够被激发,因此在随钻声波测井中可以通过选择中心频率低于二阶钻铤波截止频率的声源来减少钻铤波的干扰。如图2(b)所示,相比于快速地层,慢速地层中井壁处不再激发伪瑞利波。值得注意的是,在慢速地层中,随着频率增加,斯通利波逐渐不再趋近于井内流体速度而是更加接近于地层垂直向横波速度,且区别于慢速地层电缆斯通利波的正频散特征[25](即低频段波速快,高频段波速慢),慢地层随钻斯通利波呈负频散特征。而内斯通利波、一阶和二阶钻铤波与快速地层条件下类似,几乎不受到地层的影响。
图3给出了快速和慢速VTI孔隙地层中的随钻单极子声源激发的声压阵列波形和利用时间-慢度相关法(STC)[24]处理阵列波形数据后的结果。模拟使用的声源中心频率为7 kHz,时域脉冲长度0.5 ms。源距z= 3.0 m,接收器间距d= 0.2 m(无特殊说明,下文中阵列波形计算均采用此参数)。对于快速地层,由图3(a)可以看出,阵列波形中最先到达接收器的是钻铤波信号,并且在钻铤波尾部与地层纵波信号发生混叠;后续到达的依次是地层横波信号和斯通利波信号。根据图3(b)所示的时间-慢度相关图可以得到4个波群的慢度和到时。其中速度最快的钻铤波相关峰对应的慢度值约为200 μs/m,结合图2(a)相速度频散曲线可以确定该波群为一阶钻铤波;其次从左至右为地层纵波波群、地层横波波群和斯通利波波群的相关峰。
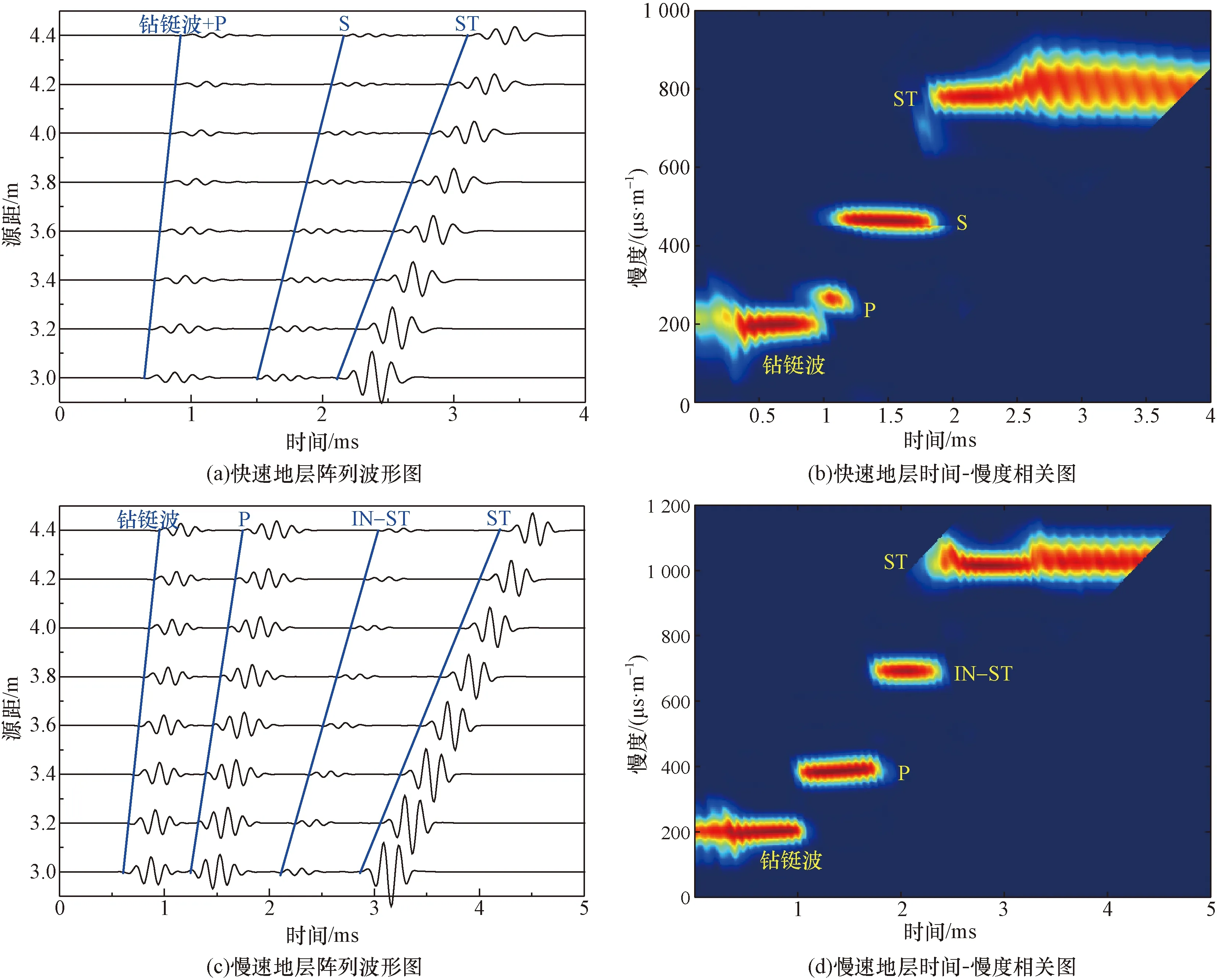
图3 VTI孔隙地层7 kHz随钻单极声波测井响应Fig.3 Acoustic response for monopole acoustic logging while drilling in VTI porous formation at 7 kHz
对于慢速地层,如图3(c)所示,阵列波形图中存在4个较为明显的波群信号,同时图3(d)处理得到了各个波群的慢度和到时。依次为一阶钻铤波,地层纵波,内、外斯通利波。相比于快速地层的情况,在慢速地层中由于地层纵波速度比较小,使其得以在时域上与一阶钻铤波分离。同时横波支点的激发能量极小,横波首波常被其余振荡信号掩盖,即为慢速地层中无法直接利用随钻单极子测量横波波速的原因。
2.2 四极子声场
图4给出了快速和慢速VTI孔隙地层中随钻四极声场的各阶模式波相速度频散曲线。对于快速VTI孔隙地层,如图4(a)所示,在声波测井常见的0~25 kHz频率范围内一共存在4种模式波。其中,“SC-1”表示的是地层一阶螺旋波(first screw wave),“SC-2”表示地层二阶螺旋波(second screw wave),两种模式波均存在低频截止现象,且低频截止速度均为地层垂直向横波速度,其中一阶螺旋波频散较强,截止频率更低,约为3.94 kHz。“C-1”和“C-2”分别表示一阶和二阶钻铤波,二者均存在低频截止现象,截止频率分别为8.92 kHz和20.96 kHz。当声源频率低于截止频率时,钻铤波将不会被激发,从而可以减少其对地层波信号的干扰。相比于快速地层,图4(b)所示的慢速地层中不存在地层二阶螺旋波,而地层一阶螺旋波仍然是以地层垂直向横波速度为低频截止速度,且截止频率向低频移动,钻铤模式波几乎不受到地层变化的影响,因此在随钻声波测井中,四极子螺旋波是测量慢速地层横波速度的有效手段[26]。
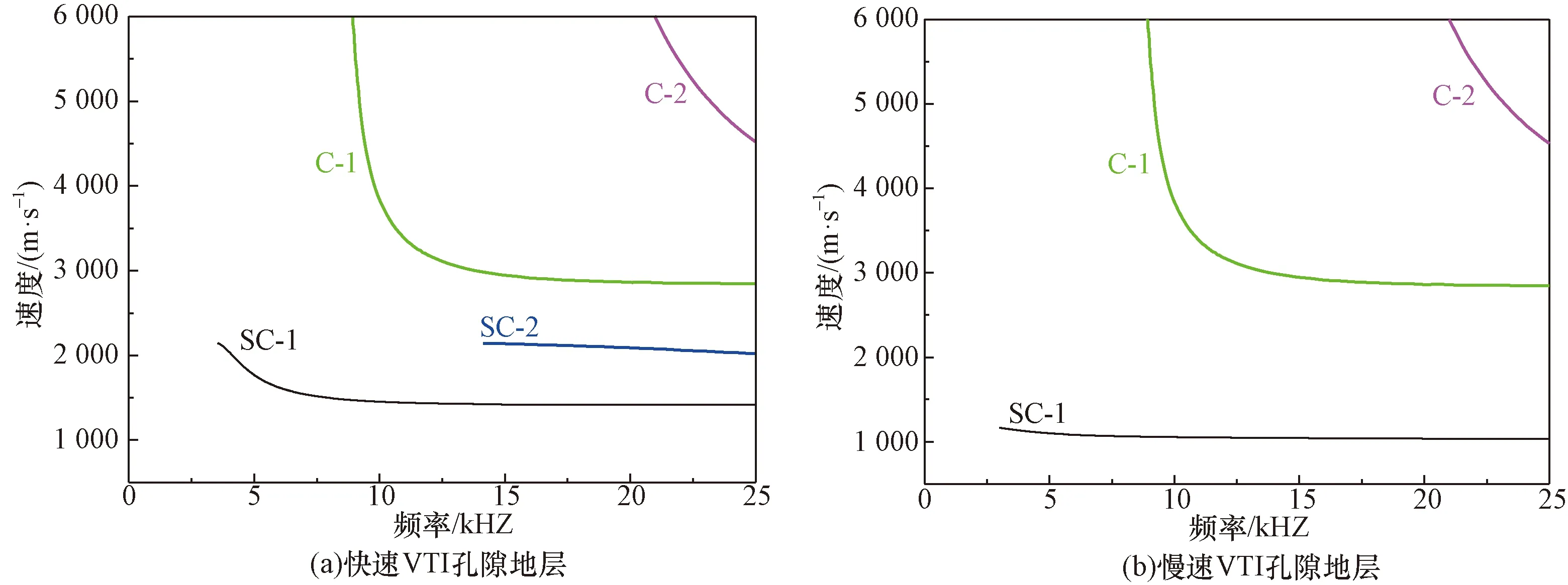
图4 随钻四极声场中的频散曲线Fig.4 The velocity dispersion curves in quadrupole acoustic logging while drilling wavefield
图5给出了快速和慢速VTI孔隙地层中的随钻4 kHz四极子声源激发的声压场阵列波形和利用时间-慢度相关法处理阵列波形数据后的结果。无论对于快速地层还是慢速地层,如图5(a)和图5(c)所示,随钻四极子阵列波形中都只出现一个波群,结合图4中的相速度频散曲线可以看出,在声源中心频率为4 kHz附近频率范围内存在模式波为地层一阶螺旋波,且由图5(b)和图5(d)得到两种地层条件下地层一阶螺旋波波群的到时和慢度,可以看出地层一阶螺旋波是以地层垂直向横波速度传播的,这也是随钻四极子横波测量的理论依据。
2.3 地层各向异性及渗透率对模式波的影响分析
储层岩石中普遍存在的各向异性和渗透性将对随钻多极子声波产生重要影响。在前述随钻声波测井理论推导的基础上,进一步考察横观各向同性孔隙地层中随钻多极子模式波的频散特征随地层各向异性和渗透率的变化规律。重点对与地层密切相关的随钻斯通利波和一阶螺旋波(简称为螺旋波)进行了分析,以快速地层为例。
图6给出了VTI孔隙地层中随钻单极斯通利波和随钻四极螺旋波的速度频散曲线在不同各向异性条件下的变化趋势。地层各向异性大小分别选取0、10%、20%、30%、40%,孔隙度选择中等孔隙度20%,水平向渗透率设定为1 000 mD,垂直向渗透率设定为100 mD。从图6中可以看出,斯通利波的相速度(虚线)与群速度(实线)均与频率呈正相关关系,即速度随着频率的增加而增加,这与螺旋波的速度变化趋势相反。随着频率的升高,螺旋波相速度减小,而群速度先减小后增加形成一个速度极小值(艾里相)。除此之外,当地层各向异性γ从0变化到40%时,二者的频散曲线都有所上升。其中,单极斯通利波在1~5 kHz频率范围内对地层各向异性的变化更为敏感。四极螺旋波的低频截止速度不受地层各向异性的影响,始终等于地层垂直向横波速度。
图7为VTI孔隙地层中随钻单极斯通利波和随钻四极螺旋波频散曲线在不同水平向渗透率条件下的响应特征。固定垂直向渗透率为100 mD(图8,二者对垂直向渗透率不敏感),地层各向异性大小为20%,孔隙度选择中等孔隙度20%,水平向渗透率分别选取500、100、50、10、5 mD。由图7所示的频散曲线可以看出,在低频段,单极斯通利波相速度随着水平向渗透率的增加而减小,且灵敏度较高;在高频段,单极斯通利波相速度随着水平向渗透率的增加而增大。相反,四极螺旋波频散曲线受地层水平向渗透率变化的影响较小。

图7 VTI地层中水平向渗透率对模式波速度频散的影响Fig.7 Effect of horizontal permeability on velocity dispersion of mode wave in the VTI formation in acoustic logging while drilling
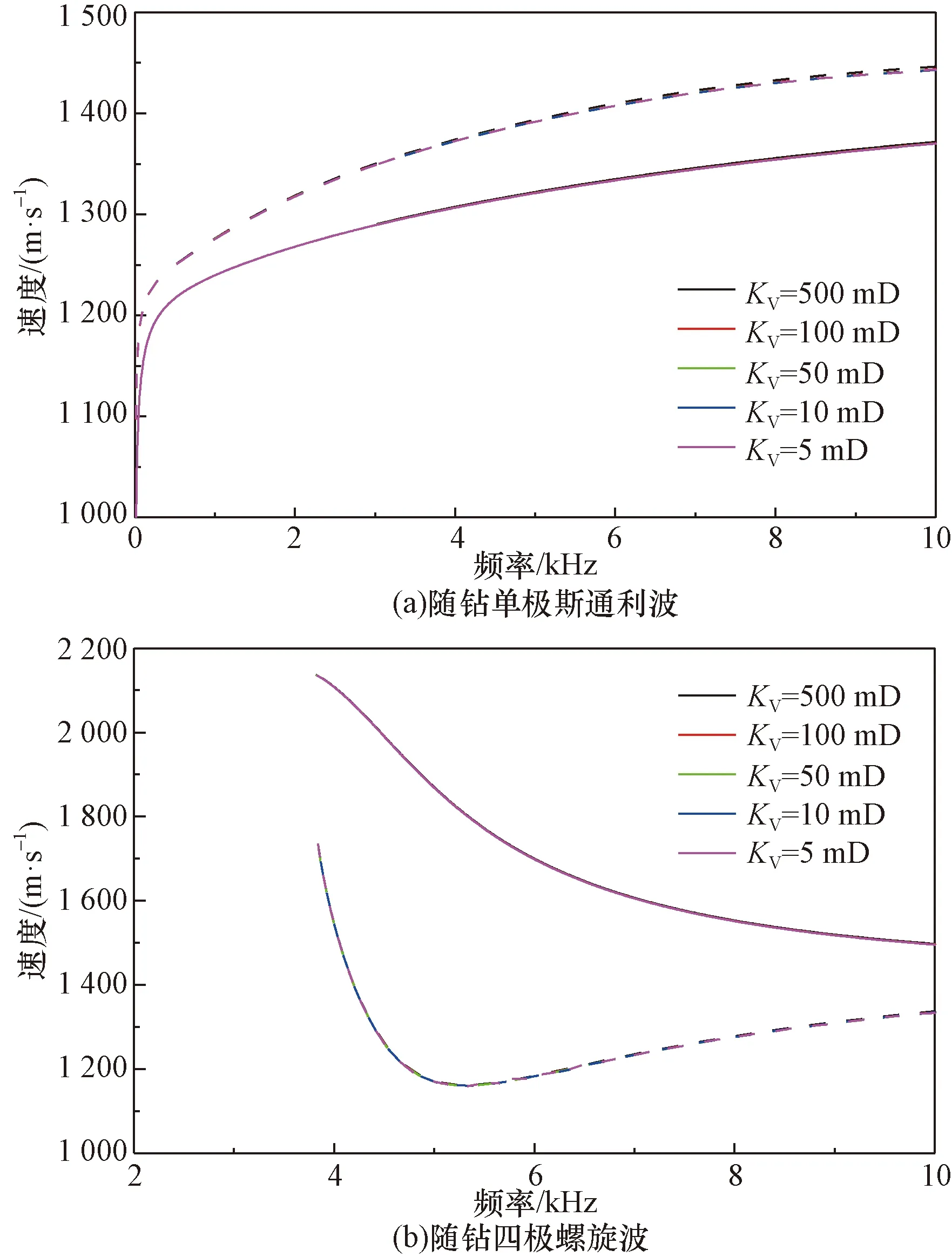
图8 VTI地层中垂直向渗透率对模式波速度频散的影响Fig.8 Effect of vertical permeability on velocity dispersion of mode wave in the VTI formation in acoustic logging while drilling
2.4 现场随钻声波测井数据处理与分析
基于理论分析,针对一口实钻井数据进行地层渗透率和各向异性的分析评价。图9为该井段处理结果,第1道给出了井径曲线和自然伽马曲线,结合第5道岩性分析可以看出该井段地层主要由砂岩和泥页岩交互层叠组成,属于典型的VTI介质。第2道给出了中子孔隙度曲线、地层密度曲线和纵波时差曲线,表明在砂岩层段孔隙性较好。第3道和第4道分别给出了随钻斯通利波和四极子波实测波形(均以变密度图的形式给出)。对该井段数据进行处理,图9中第6道给出了反演得到的地层渗透率(蓝色实线)、常规解释渗透率(黑色虚线)及岩心渗透率(红点),三者一致性较好,验证了反演结果的可靠性。第7道给出了利用STC方法由四极子阵列波形处理得到的地层垂直向横波时差(黑色实线)以及反演得到的地层水平向横波时差(红色实线)和横波各向异性(紫色填充),可以看出在该井段的页岩层段地层各向异性较高,且地层水平向横波时差与垂直向横波时差存在明显差异(绿色填充)。
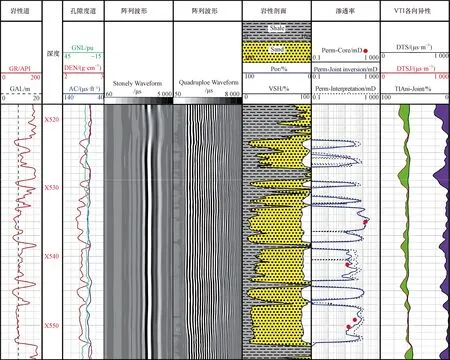
GR为自然伽马;CAL为井径;Depth为井深;CNL为中子孔隙度;DEN为密度;AC为声波时差;Stonely Waveform为斯通利波波形;Quadrupole Waveform为四极子波形;Shale代表泥岩;Sand代表砂岩;Por为孔隙度测井曲线;VSH为泥质含量;Perm-Core为岩心渗透率;Perm-Joint inversion为联合反演渗透率;Perm-Interpretation为常规解释渗透率;DTS为垂直向横波时差;DTSH为水平向横波时差;TIAni-Joint为联合反演各向异性图9 W井地层渗透率和各向异性处理分析实例Fig.9 Field data of joint inversion for permeability and anisotropy in well W
3 结论
建立VTI孔隙地层随钻声波测井模型,分别计算在快速和慢速地层中随钻多极子模式波相速度频散曲线以及理论阵列波形图,并利用时间-慢度相关法处理阵列波形得到其中各个波群的慢度和到时,结合频散曲线和阵列波形图,对随钻声波测井接收到的各振型进行分析。得出如下结论。
(1)在随钻单极声波测井中,井壁处激发的斯通利波受到井外地层变化的影响最大,内斯通利波和钻铤模式波几乎不受地层的影响,在快速地层中钻铤波信号会与地层纵波信号在时域上发生混叠,从而影响地层纵波速度的测量,而在慢速地层中接收器采集不到地层横波信号。
(2)在随钻四极声波测井中,无论是在快速地层还是慢速地层中,地层螺旋波低频截止速度均趋近于地层垂直向横波速度,且钻铤模式波也存在低频截止现象,当声源频率低于截止频率时,钻铤波将不会被激发,从而可以减少其对地层波信号的干扰,因此随钻四极子螺旋波是测量慢速地层横波速度的有效手段。
(3)实钻井资料处理结果显示地层各向异性与渗透性并存。利用随钻单极斯通利波和四极螺旋波的速度频散曲线可以对地层各向异性和渗透率进行综合评价。

