基于哈密顿力学的斜交网格筒-核心筒结构协同分析

胡启平, 宋佳乐

(河北工程大学土木工程学院, 邯郸 056038)

斜交网格结构作为一种特殊的新型建筑结构,其独特的结构形式受到越来越多的关注,应用也越来越广泛,比较著名的建筑有广州西塔、阿联酋首都门以及深圳建成的京基100等[1-4]。

高层斜交网格结构有斜交网格筒和斜交网格筒-核心筒等结构形式[1]。21世纪以来,中外学者逐渐加强了对斜交网格筒-核心筒结构的理论研究。Moon等[2]首先提出了斜交网格筒中斜柱截面初步设计的方法,并推导了结构的抗侧刚度公式,其主要思路是考虑结构中腹板的抗侧能力,忽略翼缘侧对抗侧刚度的影响,将斜交网格筒体等效为悬臂梁。滕军等[5]采用弹塑性动力时程分析法,以钢管混凝土斜交网格筒-钢筋混凝土核心筒结构为例,研究结构体系中构件的屈服顺序及内外筒抗震协同受力性能。史庆轩等[6]从结构的塑性发展过程、受力情况、变形能力、内外筒的抗侧刚度及剪力滞后等方面,对斜交网格筒-钢筋混凝土核心筒结构协同工作的受力性能进行了系统的分析。刘成清等[7-8]、方登甲等[9]通过斜交网格筒的抗侧刚度、内外筒结构的内力分布、结构的倒塌机制及延性等因素探讨结构的抗震性能,并建立相同参数的框架-剪力墙结构模型进行对比分析。张锋等[10]采用等效连续化方法将斜交网格筒等效为各向异性连续筒体,基于能量变分原理推导结构的位移场闭合解。通过进一步分析得到结构的内力和变形特征,结果表明,该类结构的变形是弯曲型和剪切型的叠加,且具有明显的剪力滞后效应。胡启平等将框筒结构、筒中筒结构等简化为具有弯曲变形和剪切变形的悬臂梁,通过哈密顿力学对结构的协同工作性能、二阶效应及动力特性进行分析,并采用精细积分法对方程进行数值求解,避免了复杂的公式推导且计算精度高[11-17]。

拟研究的斜交网格筒-核心筒结构是由斜交网格筒与开有洞口的钢筋混凝土核心筒组成的新型筒中筒结构体系,其中斜交网格筒主要通过斜柱的轴向拉压来承受竖向荷载和侧向荷载,相比于传统结构体系,该结构体系抗侧承载力高、受力情况复杂。作为一种新型结构体系,其受力特性和简化计算方法仍需深入研究。为了对斜交网格筒-核心筒结构协同工作性能进行研究,往往需对该结构进行简化处理。采用连续化方法,考虑外筒的剪力滞后效应[18-19]以及内外筒的弯曲变形和剪切变形,将斜交网格筒等效为正交各向异性连续筒体,将开有洞口的钢筋混凝土剪力墙核心筒简化为双肢剪力墙模型。

采用哈密顿力学的方法,根据勒让德变换引入对偶变量,推导协同分析的哈密顿正则方程,结合精细积分法求解结构的侧移和内力分布。将本文方法与有限元方法进行对比,以验证本文方法的正确性,通过进一步分析得出斜柱不同参数变化对斜柱轴力及内外筒结构协同工作性能的影响。该方法给斜交网格筒-核心筒结构的力学求解提供了一种新思路、新方法,为工程初步设计及后续理论研究提供参考。

1 结构简化计算模型

斜交网格筒-核心筒结构是由斜交网格筒与核心筒两种类型的抗侧力单元组成,内外筒结构在梁板的约束和协调作用下共同抵抗侧向荷载。等效连续化方法是高层建筑结构简化计算常用的分析方法,采用连续化方法将斜交网格筒等效为连续筒体,将开有洞口的钢筋混凝土剪力墙核心筒简化为双肢剪力墙模型,同时考虑内外筒的弯曲变形和剪切变形,将连接内外筒的楼板等效为刚性连杆。基于以上方法,该结构协同分析的空间模型可简化为平面模型,计算简图如图1所示,简化分析采用如下基本假定:①楼板自身平面内刚度无限大,平面外刚度忽略不计,内外筒通过刚性楼板连接,楼板的作用沿高度连续化,两者水平变形协调一致;②考虑斜交网格筒与核心筒的弯曲变形和剪切变形,将其等效为两根均匀连续的铁摩辛柯悬臂梁;③不考虑结构的扭转效应;④斜交网格筒与核心筒各层刚度保持不变。在实际工程应用中,当各层刚度变化不大时,宜采用加权平均值。

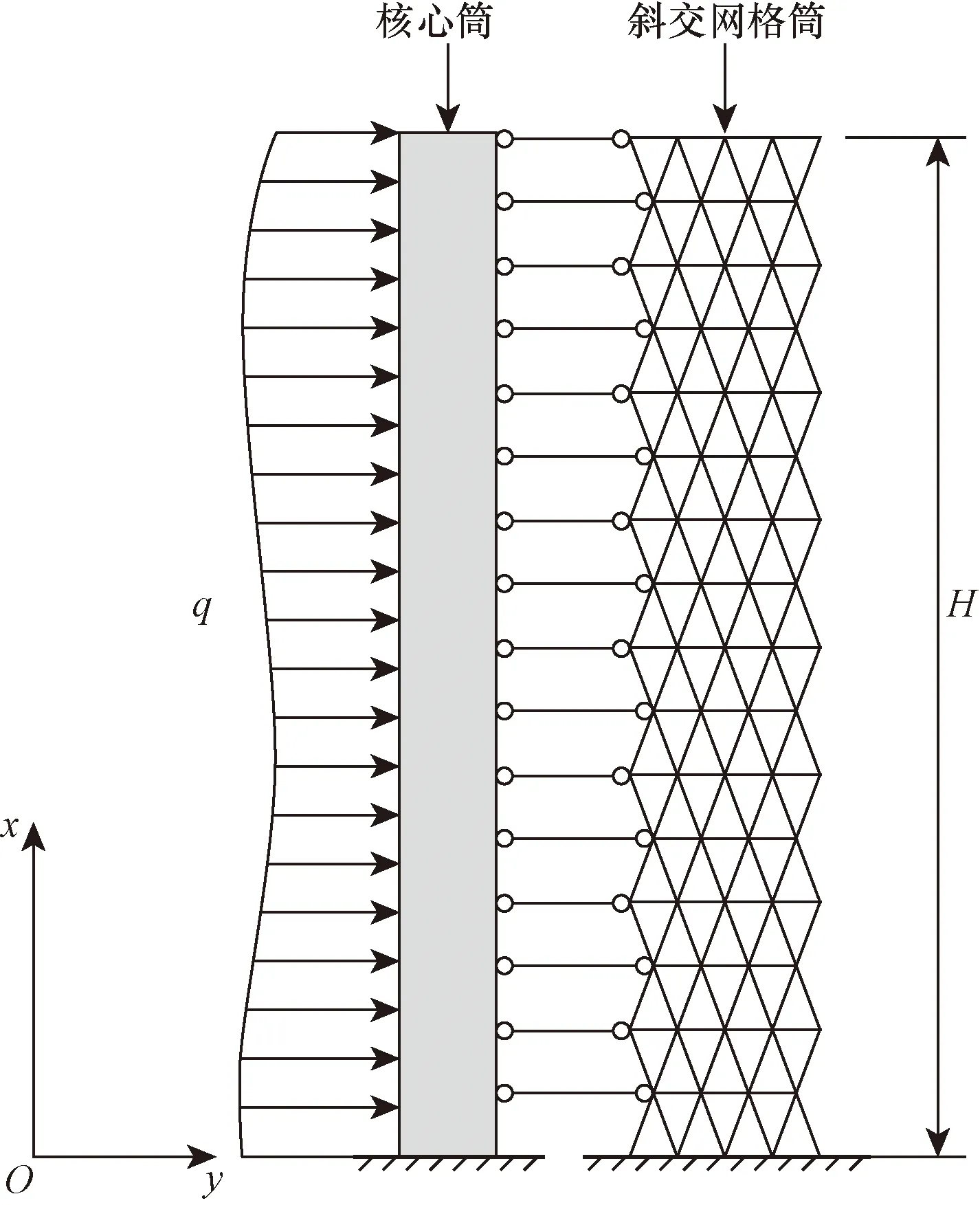
q为外荷载;H为结构楼层高度图1 高层斜交网格筒-核心筒结构计算简图Fig.1 Sketch for calculation of high-rise diagonal intersecting grid cylinder-core cylinder structure

采用文献[10]中的连续化方法将斜交网格筒中斜柱和环梁组成的稳定三角形单元等效为均匀的正交异性板,形成一个由若干正交异性板围成的实腹薄壁筒体,如图2所示。等效连续化模型计算的关键是求出等效筒体的等效弹性模量和等效剪切模量。采用连续板单元与斜交网格单元的竖向刚度和剪切刚度相等原则,推导等效连续体的等效弹性模量Eequ与等效剪切模量Gequ,其表达式分别为

(1)

(2)

(3)

式中:Ed、Ad分别为斜交网格筒中斜柱的弹性模量和截面面积;b和t分别为连续板壳单元的宽度和厚度;α为斜柱与水平面的夹角;l为斜柱间距。

内筒采用开有洞口的钢筋混凝土核心筒,其中洞口将核心筒划分为4片各自独立的“L”型剪力墙,通过连梁将它们连在一起。参考高层建筑中剪力墙的分类[20],可按照双肢剪力墙模型计算。为简化分析,采用文献[21]中双肢剪力墙等效抗弯刚度E2I2和等效抗剪刚度G2A2的计算方法,其中,E2为核心筒的弹性模量,I2为核心筒的惯性矩,G2为核心筒的剪切模量,A2为核心筒的横截面面积,具体推导过程可参阅文献。

2 位移场函数及拉格朗日函数

选取等效连续筒体的侧移v1(z)、截面转角θ1(z)、翼缘和腹板的最大纵向位移差函数W1(z)和W2(z)作为广义位移,考虑斜交网格筒的剪力滞后效应,假设结构中翼缘与腹板的纵向位移场函数分别为二次曲线和三次曲线,构造等效筒体翼缘和腹板的纵向位移场函数为

(4)

式(4)中:wf为等效连续筒的翼缘侧Z方向位移场;z、y为坐标;ww为腹板侧Z方向位移场;a为翼缘侧宽度的1/2;b为腹板侧宽度的1/2。

等效连续筒体的应变能可表示为

(5)

式(5)中:Ef、Gf分别为翼缘等效弹性模量和等效剪切模量;εzf为翼缘侧正应变;A为积分区域面积;γxz为翼缘侧剪切应变;Ew、Gw为腹板等效弹性模量和等效剪切模量;εzw为腹板侧正应变;γyz为腹板侧剪切应变;A1为斜交网格筒的积分区域。

将核心筒简化为双肢剪力墙,不考虑剪力滞后效应。选取核心筒的侧移v2(z)、截面转角θ2(z)作为广义位移,剪力墙的纵向位移符合平截面假定,位移场为

w=-yθ2(z)

(6)

核心筒的应变能为

(7)

式(7)中:A2为核心筒的积分区域;E2为核心筒的弹性模量;εz为核心筒的正应变;G2为核心筒的剪切模量;γz为核心筒的剪切应变。

由于刚性楼板的作用,内外筒两个抗侧力体系水平变形协调,即v(z)=v1(z)=v2(z)。

当结构上作用沿高度变化的侧向荷载q(z)时,结构的外力势能为

(8)

结构的总势能为

Π=Π1+Π2+Π3

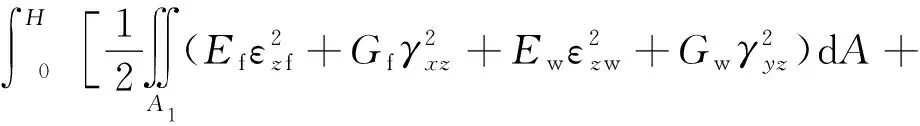
(9)

结构的总势能密度表达式即为斜交网格筒-核心筒结构协同分析的拉格朗日函数为

(10)

式(10)中的应变分量可由位移场函数和弹性力学的几何方程求出,整理后拉格朗日函数的矩阵表达式为

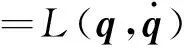
(11)

3 哈密顿对偶体系

通过勒让德变换,引入广义位移q的对偶变量p,p的物理意义即为广义位移对应的广义力。其表达式为

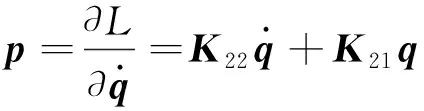
(12)

将问题由拉格朗日力学体系转变到哈密顿力学体系,导出哈密顿函数为

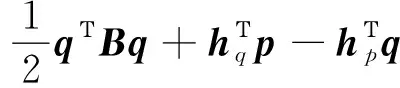
(13)

由式(13),得到哈密顿正则方程[22]为

(14)

4 结构内力计算

通过对实腹筒体断面应变积分,求出斜柱相交节点位置的内力,再利用相交节点的平衡关系可以得到斜柱的轴力。翼缘侧平面相交节点的竖向力Nz与水平力Qz可分别表示为

(15)

式(15)中:xj为翼缘侧相交斜柱的平面节点位置;lf为翼缘侧相交斜柱柱距。

腹板侧平面相交节点的竖向力与水平力为

(16)

式(16)中:yj为腹板侧相交斜柱的平面节点位置;lw为腹板侧相交斜柱柱距。

利用式(15)和式(16),结合节点平衡条件,求出高度z处的斜柱轴力为

(17)

5 计算实例

某外筒采用斜交网格筒,内筒采用开洞的钢筋混凝土核心筒的筒中筒高层建筑结构共54层,层高为3.9 m,总高度为210.6 m。外筒平面尺寸为36 m×36 m,斜柱柱距为9 m,与水平面夹角α=69°,截面为箱形,尺寸为800 mm(宽)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚),环梁截面也为箱形,尺寸为300 mm(宽)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚),外筒材料弹性模量Ed为206 GPa。内筒平面尺寸为18 mm×18 mm,墙肢宽度为8 m,连梁高度为1 m,墙肢厚度为0.4 m,混凝土采用C60;结构承受顶点集中荷载101.4 kN。

按2～4节的方法算出简化计算模型对应的各个物理量后,即可确定式(14)。利用MATLAB编程采用精细积分算法可以快速计算出广义位移和广义力,进而得到协同分析所需的结构侧向位移及各项内力。

为了验证本文方法的正确性,采用ETABS软件对高层结构进行了有限元分析。在有限元程序中,采用刚架单元模拟斜柱和环梁,墙单元模拟核心筒剪力墙。两种方法计算结果对比如图3～图6所示。两种方法计算结果除少数数据外,相对误差都小于5%。

图3 结构侧向位移Fig.3 Lateral displacement of structure

由图3的侧移可以发现,斜交网格筒-核心筒结构的侧向变形为“弯曲型”。

斜交网格筒-核心筒结构楼层弯矩分布如图4所示,内外筒的楼层最大弯矩均作用在基底处,且随着楼层的增加而减小,外筒各楼层弯矩明显大于内筒,因此外筒承担更多的弯矩,为结构的主要抗弯构件。结构楼层剪力分布如图5所示,有限元方法分析得到的内外筒楼层剪力存在起伏变化。而由于本文方法采用连续化假定,无法反映实际受力状态下楼层剪力的突变,因此内外筒剪力没有起伏变化,计算得到的结构剪力近似为定值。结构中内筒的最大剪力作用在基底处,随着楼层的增加而减小,外筒的剪力随楼层的增加而增大,除底部少数楼层外,外筒承担更多的剪力,为结构主要的抗剪构件。

图5 结构楼层剪力分布Fig.5 Shear force distribution of structural floors

标高z=11.7 m处节点力与斜柱轴力分布如图6所示。可以看出,本文方法与有限元计算结果吻合良好。在侧向荷载作用下,结构中的斜柱主要承受轴力作用,腹板侧存在受压区与受拉区,两区域相互重叠,导致内力图中腹板侧斜柱轴力存在起伏变化。翼缘侧斜柱内力是由腹板侧斜柱内力通过角部相交斜柱传递而来,内力的传递途径在转角处发生转折,传递而来的轴力交叉分配到翼缘侧的斜柱上。基于相交节点竖向力对斜交网格筒-核心筒结构剪力滞后效应进行研究,整个分析过程简便,更能体现结构的整体内力分布。从图6中可以看出,斜交网格筒-核心筒结构具有明显的剪力滞后效应。

图6 顶点集中荷载作用下内力结果对比Fig.6 Comparison of internal force results under concentrated load at the vertex

本文方法得到斜柱区段标高处的剪力和弯矩如表1所示。

表1 结构的剪力和弯矩Table 1 Structural shear force and bending moment

6 协同工作影响因素分析

斜交网格筒-核心筒结构作为一种新型的双重抗侧力结构,其受力机理与传统结构不同,斜交网格筒-核心筒结构具有较强的弯曲刚度和剪切刚度。通过理论研究发现,斜交网格筒和核心筒的弯曲刚度与剪切刚度对结构的侧向位移及内力影响较为明显。外筒刚度的控制因素为斜柱角度和斜柱的截面尺寸,本节通过改变斜柱截面尺寸来研究斜交网格筒-核心筒结构协同工作性能的影响。

对上述算例模型中斜交网格筒的斜柱截面进行调整,截面由原始的800 mm(宽)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚)改变为1 000 mm(宽)×1 000 mm(高)×40 mm(壁厚)×40 mm(壁厚)和600 mm(宽)×600 mm(高)×20 mm(壁厚)×20 mm(壁厚),分析结果如表2所示。

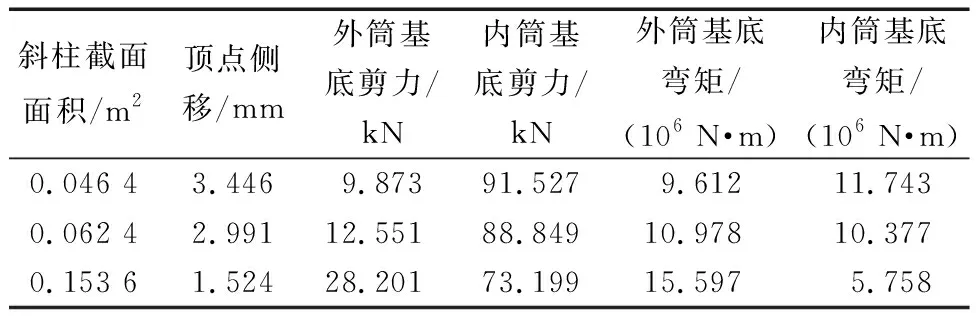
表2 不同斜柱截面下结构的侧移和内力Table 2 Side displacement and internal force of the structure under different inclined column sections

从表2数据中可以看出,当斜柱截面面积减小25%时,结构的顶点侧移增大13%。随着斜柱截面面积的减小,斜交网格筒的刚度逐渐减小,结构的整体弯曲侧移和剪切侧移增大。当斜柱截面面积较小时,基底的弯矩和剪力主要由核心筒承担。相反地,当斜柱截面面积增大59%时,结构的顶点侧移减小49%。随着斜柱截面面积的增加,斜交网格筒承担的弯矩和剪力逐渐增大,成为结构中主要的抗弯构件和抗剪构件。研究表明,斜柱截面面积对斜交网格筒-核心筒结构的协同工作性能有显著影响。

7 结论

(1)哈密顿力学提出斜交网格筒-核心筒结构协同分析新方法,并采用精细积分法求解出高精度数值解,理论推导过程便捷。与有限元方法对比,数值吻合良好,一般相对误差不超过5%,验证了本文方法的正确性。该方法可在结构初步设计阶段对结构方案进行快速分析验证。

(2)斜交网格筒-核心筒结构在水平荷载作用下的侧向变形呈“弯曲型”。区别于一般的框架-核心筒结构,斜交网格筒-核心筒大部分的楼层剪力和弯矩由斜交网格筒承担。除底部少数楼层外,其余楼层剪力沿高度变化不大。

(3)斜交网格筒-核心筒结构具有明显的剪力滞后效应,本文方法能够较准确地分析剪力滞后效应的影响。

(4)分析了斜交网格筒-核心筒结构的斜柱截面面积对内外筒结构协同工作的影响。结果表明,当斜柱的截面面积增大,侧移将明显减小,斜交网格筒承担的弯矩和剪力增大,成为结构的主要抗弯构件和抗剪构件。