基于量纲分析的戈壁地区爆破振动衰减模型
李贺龙, 王浩, 诸洲, 张建经, 郭建婷, 牛家永
(1.中核华辰建筑工程有限公司, 西安 712000; 2.中铁北京工程局集团有限公司工管中心, 北京 102308; 3.西南交通大学土木工程学院, 成都 610031; 4.宁夏水利科学研究院, 银川 750021)
随着中国经济建设的蓬勃发展和爆破技术的不断进步,工程爆破广泛应用于矿山、水利水电、交通、建筑等领域[1],成为一种不可或缺的工程施工手段。它在带来巨大社会经济效益的同时,工程爆破也给周围的人员、设备、建(构)筑物以及环境带来了不可忽略的负面效应[2]。爆破振动的破坏作用是工程爆破负面效应中最重要的问题之一[3],已引起中外研究者和工程技术人员的广泛关注[4-5]。
萨道夫斯基公式在中外应用广泛,中国的《爆破安全规程》(GB6722—2014)也采用这一公式计算相应的物理量。由于影响爆破振动传播和衰减规律的因素十分复杂,对于不同地区的爆破工程,其地质特征和爆破参数差异较大,且中国大部分衰减模型参数更适用于爆破工程开展次数较多的南方地区[6]。对于戈壁地区的重要工程,由于在历史上开展的爆破施工相对较少,无相关数据可供参考,因此需要根据项目所在地的地质和地形条件建立该地区的衰减模型,为爆破方案设计提供指导。工程实践表明,平整地形条件下的萨道夫斯基公式预测质点爆破振动速度精度较高,而在地形地貌变化较大的爆破工程场地,萨道夫斯基公式预测精度则较低[7]。仅考虑装药量和爆心距两个因素得到的计算公式往往精度不高,所以很多学者在特定工程条件下对萨道夫斯基公式进行修正[8]。大范围的岩石场地基坑开挖需要进行多次爆破施工,这将导致爆破场地的地形地貌发生较大变化,加之戈壁地区具有特殊的地质条件,因此需要建立具有区域特征的爆破振动速度预测公式[9]。但是,目前尚无可综合考虑戈壁地区地质、地形等影响因素的爆破振动公式。
目前中外计算爆破振动速度时普遍采用爆破振动速度的大小与比例药量(Q1/3/R,其中,Q为一次起爆总药量,R为测点至爆源的距离)的α次方(α为衰减指数)成正比的萨道夫斯基公式。然而萨道夫斯基公式的建立是基于球形药包洞室爆破的大量实测数据经统计分析得到,该公式对球形药包引起的爆破振动速度预测比较准确[10]。目前柱状药包广泛应用于中外大型爆破工程中,它和常用的球形药包相比具有爆堆集中、地震效应小、抛掷距离远、爆破方量多、破碎度更均匀等优点[11]。对于柱状药包而言,不同装药方式对爆破振动有很大的影响[12],利用球形药包爆破所推导出的公式计算柱状药包诱发的爆破振动速度,显然存在较大的缺陷。深孔柱状装药的起爆方式通常为逐排起爆,成排炮孔的分散药包爆炸诱发的地震波与单一药包不同,如果简单地将分散药包假设为集中药包进行爆破振动速度计算,将会产生明显的误差。当爆破施工现场周围有重要的构筑物时,由于构筑物与爆破场地的距离较近,逐排起爆时爆破地震波具有明显的叠加效应,按照集中药包进行计算将低估爆破振动速度[13]。
现以宁夏危险废弃物处理中心建设项目的基坑爆破开挖为工程背景,基于大量的现场监测数据建立戈壁地区的爆破振动速度衰减模型。为了提高模型精度,通过考虑装药特征对爆破振动的影响,基于量纲分析理论推导出成排深孔爆破振动速度预测公式,并与实测结果进行对比分析,以验证所提出爆破振动公式的准确性。研究成果可应用于戈壁地区露天深孔爆破工程的设计与振动控制。
1 工程概况现场监测结果分析
1.1 工程概况
宁夏危险废弃物处理中心建设项目位于宁夏石嘴山市北部的戈壁地区,根据工程现场的实际情况及设计要求,选取垂直高度上一次性大断面爆破和分层爆破两种施工方案。由项目所在区域的地形地质条件、周围环境、施工工期、施工要求以及周边子项对爆破振动的要求,首先应对一期M-1、M-3、M-5、M-7、M-9和M-10子项周边9 m范围内的石方进行机械破碎(无法满足爆破振动对主体结构的影响),再实施A、B、C区域的爆破施工,区域分层爆破如图1所示。
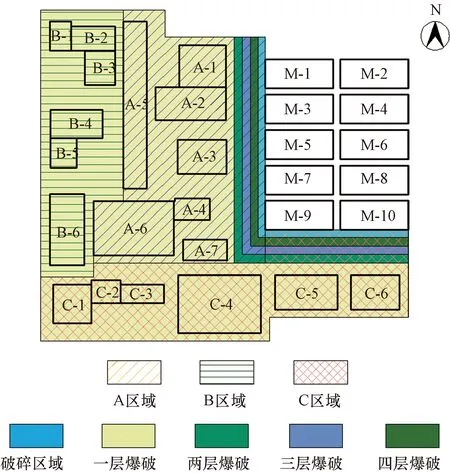
图1 区域分层爆破示意图Fig.1 Schematic diagram of regional layered blasting
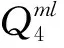
1.2 基坑爆破监测
本次爆破振动监测获取了大量的振动测试数据,为了保证监测结果的统一性,选取爆破区域地形条件相似,起爆联网方式相同、爆破参数及药量大致相同、外部因素影响较小的7次爆破振动监测进行分析,对信号进行预处理后,共获取22组有效监测数据。选取其中一次典型爆破监测方案为例进行说明,C-4段基坑采用一次性大断面爆破,起爆方式为从南到北逐排起爆,爆破孔网参数具体为:①炮孔采用垂直孔,炮孔直径为90 mm,炮孔深度为14 m;②炮孔超深深度为1.1 m,即测点与基坑底部的高程差为12.9 m;③垂直平行孔的密集系数为1.2;④最小抵抗线为2 m;⑤炮孔孔距为3 m,炮孔排距为2.5 m;⑥填塞长度为2.7 m;⑦炸药单耗为0.35 kg/m3,炮孔单孔装药量为36.7 kg;⑧炮孔内选用秒发雷管,同一排炮孔之间选用即发雷管,排间选用接力雷管Ms5(110 ms);炮孔和监测点具体位置如图2所示。

图2 爆破炮孔及测点布置图Fig.2 Layout of blasting holes and measuring points
1.3 爆破振动速度衰减规律
中国爆破工程大多根据现场实测数据对萨道夫斯基公式中的未知参量K和α进行回归分析,得到爆破振动速度衰减规律。式(1)为中国现行《爆破安全规程》(GB 6722—2014)[14]中采用的萨道夫斯基公式。
(1)
式(1)中:V为质点振动速度幅值;Q为一次起爆总药量;R为测点至爆源的距离;K和α分别为与爆破现场地形、地质条件有关的特征系数和衰减指数。
根据现场实测数据回归得到萨道夫斯基公式中的系数K和衰减指数α,水平径向、水平切向和垂直向的爆破振动速度衰减公式如表1所示。图3为水平径向和垂直向振动速度的回归曲线。可以看出水平径向、垂直向的振动速度V与比例距离R/Q1/3呈指数衰减关系。当R/Q1/3的值小于4时,振动速度衰减较快,当R/Q1/3的值大于4时,振动速度衰减趋势减弱,且逐渐趋于平缓。水平径向振动速度整体略大于垂直向振动速度,由于爆破振动测试场地为逐排深孔爆破,炮孔中的柱状药包爆炸激起平行于地面方向传播的柱面波,所布置的测点距爆区较近,柱面波特征比较明显,在柱状波阵面作用下,水平径向振动速度整体上略大于垂直向振动速度。

表1 爆破振动速度衰减公式Table 1 Attenuation formula of blasting vibration velocity
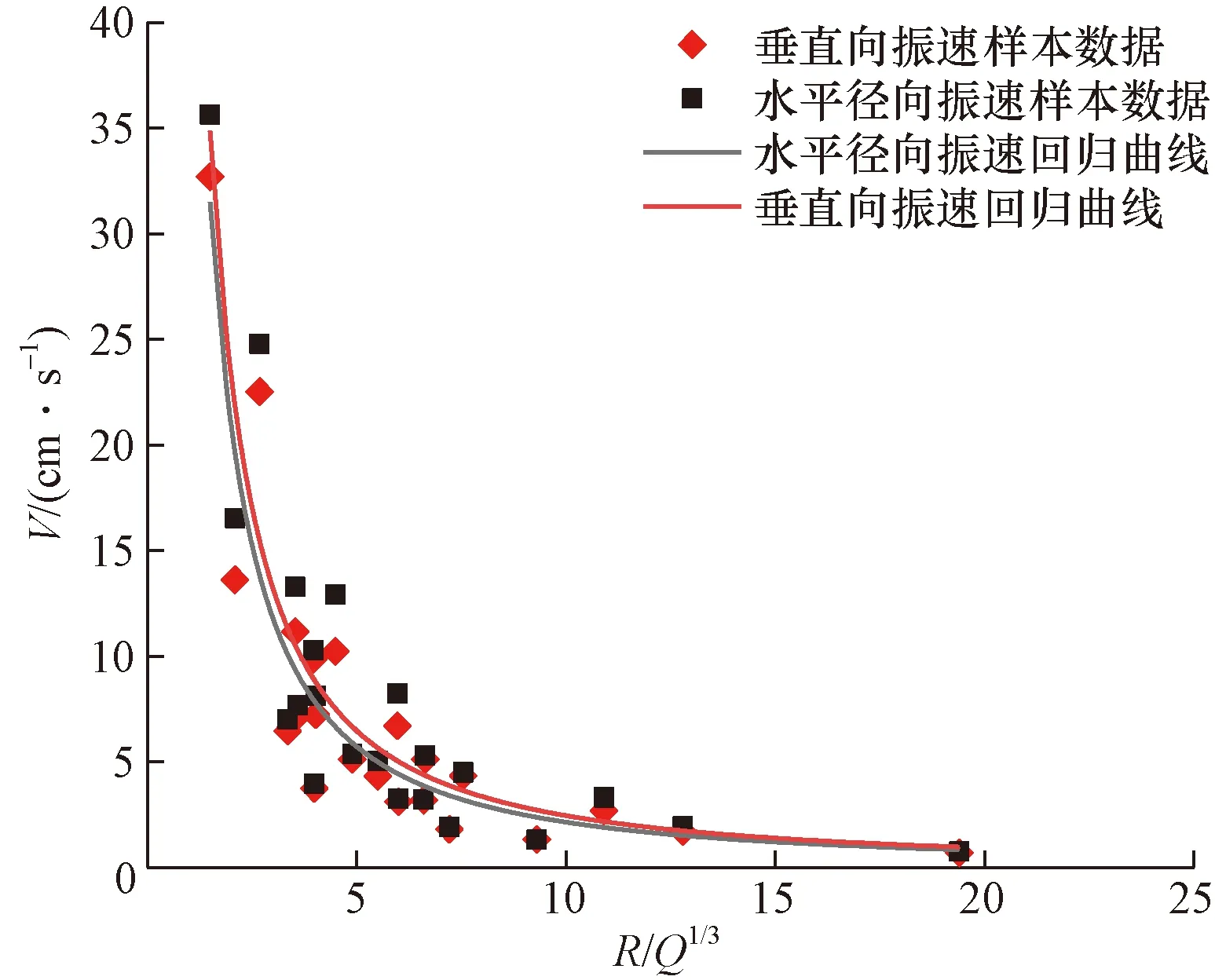
图3 水平径向和垂直向的振动速度回归曲线Fig.3 Horizontal radial and vertical vibration velocity regression curves
2 爆破振动速度的量纲分析
2.1 公式推导
爆破地震波引起地面振动是一个复杂的过程,受很多因素影响,如装药量、装药类型、装药结构、爆源与测点间的距离、地形与地质、岩土性质等[15-17]。按照几何参数、岩石参数、炸药参数进行分类,根据基坑爆破开挖现场的地形地貌和起爆网络,以计算结果与实测结果尽可能接近为目标,选取影响爆破振动速度的因素,如表2所示。
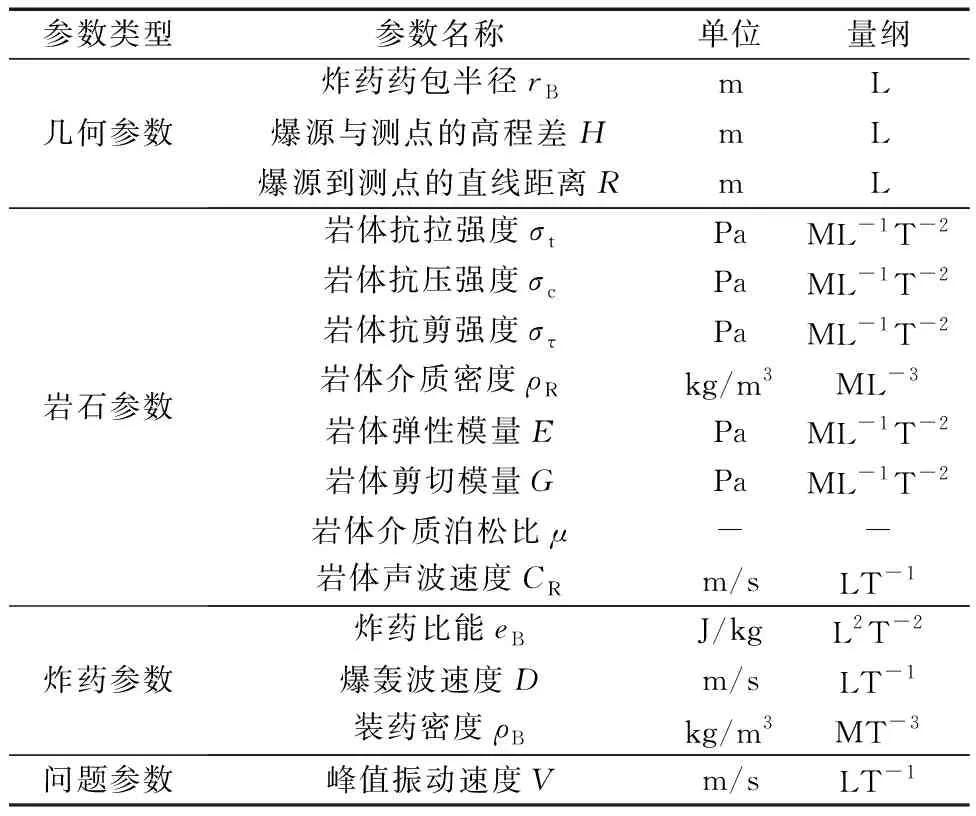
表2 爆破振动速度衰减规律的影响因素Table 2 Influencing factors of blasting vibration velocity attenuation law
从表2可以看出,表征爆破振动速度的参数很多,完全考虑所有参数会导致量纲分析得到的无量纲变量函数异常复杂。根据基坑爆破开挖现场的地形地貌和爆破条件,推导平整场地条件下,逐排深孔爆破引起的质点振动速度计算公式,所以,此处选取药包半径(rB)、测点到成排炮孔几何中心的直线距离(R)、单排炮孔连线长度(S)、炸药密度(ρB)、爆轰波速度(DB)、岩体密度(ρR)、岩体声波速度(CR)和岩体弹性模量(ER)8个主要影响因素作为自变量,运用量纲分析理论构建爆破振动速度V的预测公式。成排深孔爆破几何示意图如图4所示。
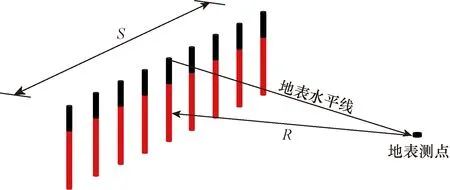
图4 成排深孔爆破几何示意图Fig.4 Geometric diagram of row deep hole blasting
在量纲分析中,爆破振动速度与多个物理量具有函数关系,可表示为
V=Φ(rB,R,S,ρB,DB,ρR,CR,ER)
(2)
所分析问题的物理量参数n=9,取炸药密度(ρB),爆轰波速度(DB)测点到成排炮孔的垂直距离(R)为独立量纲,独立量纲数m=3,因此可以用n-m=7个无量纲数组πi(i=1,2,…,6)来表示上述物理量参数。根据π定理可得
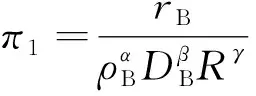
(3)
式(3)中:α、β、γ为待定系数。
因为π是无量纲量,所以式(2)中分子分母的量纲相等,由ρB、D、R与rB的量纲可得
dimrB=L=(ML-3)α(LT-1)β(L)γ
(4)
式(4)中:对于L有γ=1;对于T有α=β=0。
则有
(5)
同理可得
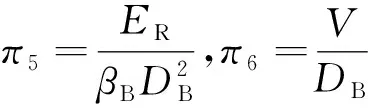
(6)
将式(5)和式(6)代入式(2)可得
(7)
实际工程中,对于同一爆破场地,其炸药种类、装药密度和岩体特性变化不大,可以将炸药密度(ρB)、岩体密度ρR、岩体声波速度(CR)、爆轰波速度(DB)和岩体弹性模量(ER)近似看为常数。因此,式(7)可简写为
(8)
不同无量纲数π的乘积和乘方仍为无量纲数,令:
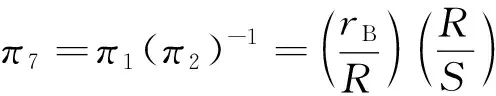
(9)
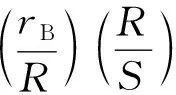
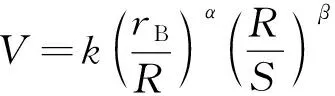
(10)
对于球形药包,其药包半径在炸药密度不变的情况下可以表示为药量的立方根,即rB≌Q1/3。因此,球形药包成排孔同时起爆的振动速度预测公式可写为
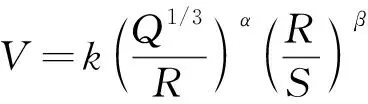
(11)
式(11)中:V为峰值质点振动速度,m/s;k为与爆源至测点间的地形、地质条件有关的影响系数;Q为一次起爆总药量,kg;R为测点至爆源的距离,m;α为柱状药包比例距离影响系数;S为单排炮孔连线长度,m;β为成排炮孔同时起爆影响系数。
当测点与爆源的距离很远时,成排孔中各药包到测点的距离很接近,若此时将分散药包当作集中药包计算,式(11)可写为
(12)
式(12)即为当前中国广泛使用的萨道夫斯基公式。
对于柱状药包,其药包半径在装药密度不变的情况下可以表示为药量的平方根,即rB≌Q1/2,由式(10)可知,柱状药包成排孔同时起爆的振动速度预测公式可写为
(13)
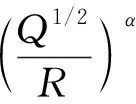
2.2 公式回归拟合
将式(13)两端取对数,使其线性化,可得
(14)
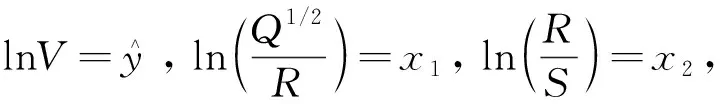
lnk=c,a=α,b=β,则式(14)可表示为
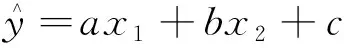
(15)
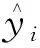


(16)
利用数学分析中的极值原理,求使偏差平方和δ取最小值时所对应的系数a、b、c的值。若使式(16)偏差平方和最小,则其必要条件为
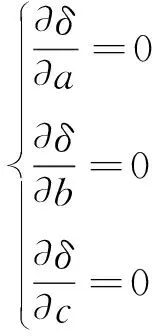
(17)
即
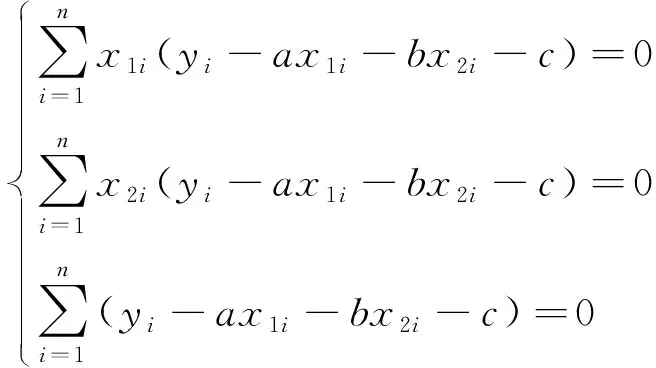
(18)
整理式(18)得
(19)
式(19)中:n为第n个实测值。
将现场实测数据代入式(19)中的三元一次方程组即可求得回归方程[式(15)]中的系数a、b、c的值,进而求得式(13)中k、α、β的值,得到成排深孔爆破振动速度预测公式。
2.3 预测结果对比分析
所推导的逐排深孔爆破振动速度计算公式建立了爆破振动速度与其主要影响因素之间的数学关系,通过和传统的萨道夫斯基爆破振动速度预测公式对比预测精度,验证本文公式的准确性和有效性。采用计算值与实测值之间的相对误差来衡量爆破振动速度预测公式计算值的预测精度,相对误差按式(20)计算。

(20)
式(20)中:Vy为预测振动速度;Vt为实测振动速度。
利用现场实测数据回归得到式(13)水平径向、水平切向和垂直方向上的爆破振动速度预测公式分别为
(21)
(22)
(23)
式中:Vra、Vta、Vve分别为水平径向、水平切向和垂直方向上的爆破振动速度。
所推导的爆破振动速度预测公式与传统萨道夫斯基公式在水平径向、水平切向、垂直向上计算结果的相对计算误差分别如表3~表5所示。

表3 水平径向爆破振动速度计算公式相对误差Table 3 Relative error of calculation formula for vibration velocity of horizontal radial blasting
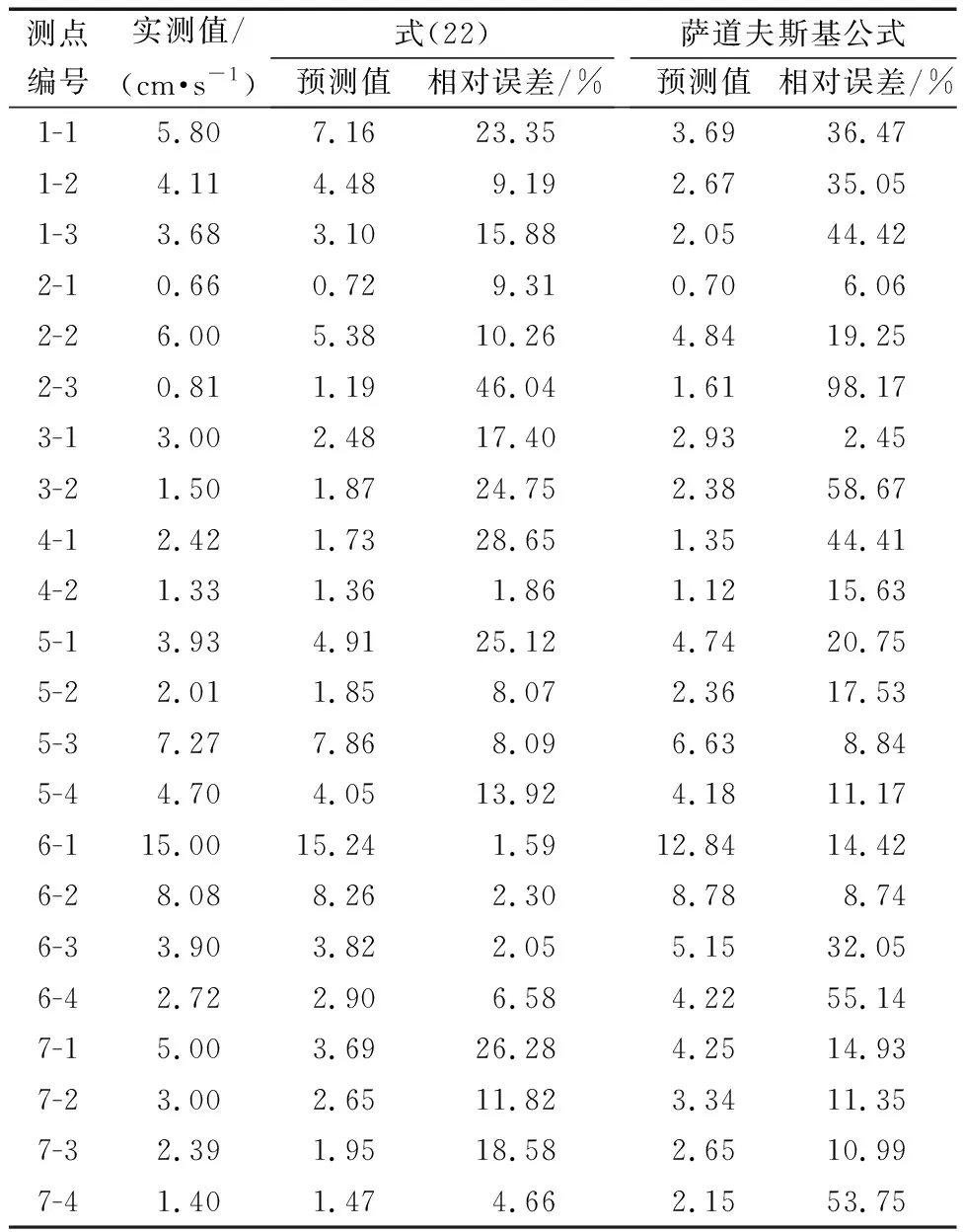
表4 水平切向爆破振动速度计算公式相对误差Table 4 Relative error of calculation formula for vibration velocity of horizontal tangential blasting
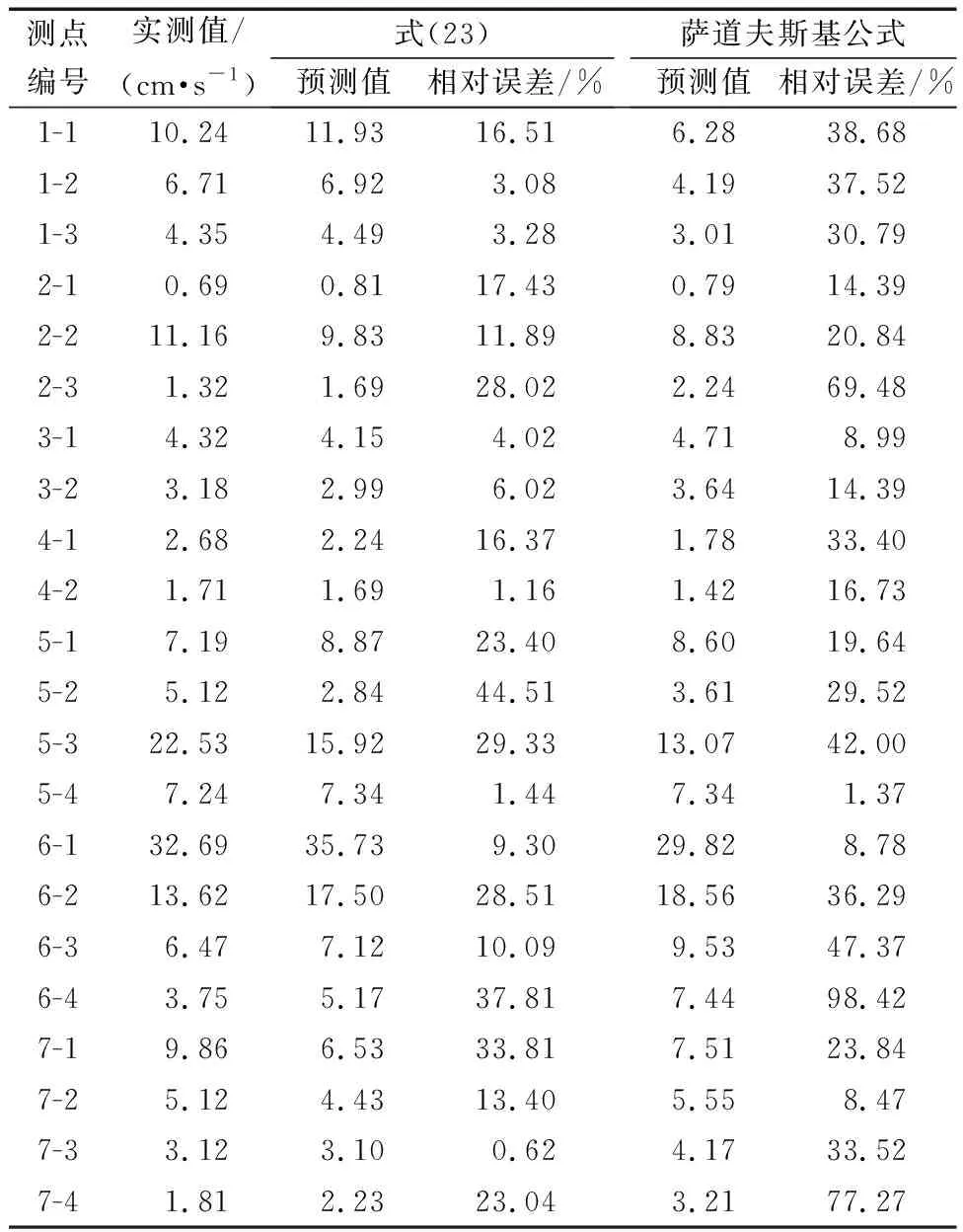
表5 垂直向爆破振动速度计算公式相对误差Table 5 Relative error of calculation formula for vibration velocity of vertical blasting
由表3~表5可知,所推导的爆破振动速度预测公式计算得到的水平径向、水平切向和垂直向爆破振动速度平均相对误差分别为17.36%、14.35%、16.50%,而萨道夫斯基公式预测得到的水平径向、水平切向和垂直向爆破振动速度平均相对误差分别为34.95%、28.19%、32.35%。可知成排深孔爆破条件下用本文推导的公式预测爆破振动速度误差较小,采用萨道夫斯基公式预测误差较大,萨道夫斯基公式预测值的平均相对误差约为本文推导爆破振动速度预测公式的2倍。因此,本文推导得到的爆破振动速度预测公式能较准确地反映平整场地条件下成排深孔爆破振动速度的衰减规律。
3 结论

(2)将推导得到爆破振动速度预测公式与萨道夫斯基公式进行现场应用对比分析,结果发现新推导公式的水平径向、水平切向和垂直向振动速度预测精度均高于萨氏公式,萨道夫斯基公式预测值的平均相对误差约为新推导公式的两倍。说明推导得到的爆破振动速度预测公式能较准确地反映平整场地条件下成排深孔爆破振动速度的衰减规律。

